脈沖路面下電動汽車主動懸架狀態(tài)反饋H∞控制

李杰，賈長旺，成林海，趙旗

（吉林大學汽車仿真與控制國家重點實驗室，吉林長春 130025）

與集中式電動汽車相比，輪轂電機電動汽車簡化了傳動結構，驅動響應快、驅動控制精確和各個車輪獨立可控，是底盤優(yōu)化和控制的理想載體［1-3］.然而，輪轂電機也帶來平順性負效應問題［4-6］.

針對輪轂電機平順性負效應問題，已經提出了多種改善方法，涉及輪轂電機輕量化、懸架優(yōu)化、動力吸振器應用、懸架控制等方面.輪轂電機輕量化是從電機設計方面考慮電機減振［7］，可以減輕非簧載質量，但是難以改變安裝電機后汽車發(fā)生的變化.懸架優(yōu)化是通過關鍵參數優(yōu)化和結構改進減輕輪轂電機帶來的平順性負效應［6，8］，只能針對特定的路面和車速實現(xiàn)優(yōu)化，無法全面適應路面和車速的各種變化.動力吸振器可以減少輪轂電機的振動［9］，但會產生在車輪內布置困難和結構復雜化的問題.懸架控制主要圍繞懸架控制策略設計和執(zhí)行器開發(fā)等展開，輪轂電機電動汽車可以采用PID［10］、模糊［11］、天棚［12］、地棚［13］、天棚地棚混合［13］、最優(yōu)［14］和H∞［15］等控制策略，目前主要針對單輪實現(xiàn)懸架控制，缺乏考慮前后車輪和空間車輪懸架控制的研究，也沒有考慮電機偏心的影響.懸架控制執(zhí)行器開發(fā)是通過半主動懸架［16］和主動懸架［17］實現(xiàn)的，半主動懸架執(zhí)行器目前主要采用磁流變阻尼器［11］，通過控制阻尼力實現(xiàn)，需要外部能量較少；主動懸架主要包括電磁執(zhí)行器［13］和液壓執(zhí)行器［15］，一般通過輸入電能產生主動力，需要外部能量較大.

作為改善輪轂電機平順性負效應的一種有力措施，主動懸架具有控制更好的優(yōu)點.然而，主動懸架應用需要解決內部不確定性和外部干擾影響的魯棒控制問題［18］，輪轂電機電動汽車主動懸架魯棒控制，即H∞控制的研究還有待深入開展.

當汽車在道路上行駛時，會遇到脈沖路面，如道路上的凸起或減速帶等障礙.雖然脈沖路面的作用時間較短，但會使汽車振動突然加大，立刻降低乘員舒適性，還會對車輛零部件和運載貨物造成損傷或破壞.以往的研究較少考慮脈沖路面對輪轂電機電動汽車平順性的影響，針對輪轂電機電動汽車脈沖路面平順性開展研究，將使輪轂電機電動汽車平順性的研究更加全面.

本文研究輪轂電機電動汽車狀態(tài)反饋H∞控制問題，考慮脈沖路面和輪轂電機實現(xiàn)脈沖路面主動懸架和被動懸架的平順性對比分析.

1 輪轂電機電動汽車振動模型

1.1 脈沖路面車輪激勵

GB∕T 4970—2009 規(guī)定［19］，脈沖路面車輪激勵由三角形凸塊確定.脈沖路面前輪激勵qf(t)為：

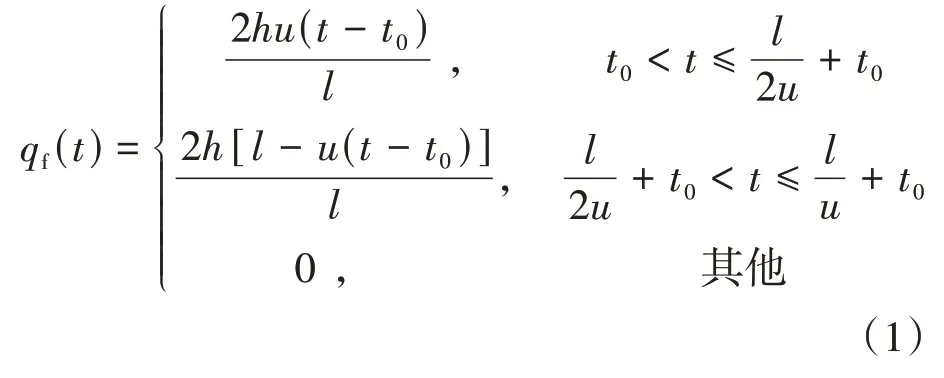
式中：u為車速；h為凸塊高度；l為凸塊長度；t0為汽車以車速u行駛時前輪到達凸塊的時間.脈沖路面后輪激勵qr(t)為：

式中：L為車輛軸距；td為后輪滯后前輪的時間.

1.2 輪轂電機激勵

選取典型的四相8∕6 極開關磁阻電機作為輪轂電機，其垂向激勵為單相轉子垂向激勵之和［13，20］，即

式中：Fv為電機垂向激勵；Fvj分別為6 個單相轉子a、b、c、a′、b′和c′的垂向激勵.

1.3 車輛模型

以往研究輪轂電機電動汽車平順性，多采用汽車二自由度振動單輪模型，具有可以揭示基本概念、基本性能和分析簡單明確等優(yōu)點.然而，二自由度振動單輪模型反映的是汽車一個角的作用，即單個車輪及其上面部分簧載質量的作用，只能用于研究簧載質量和車軸非簧載質量的垂直振動，無法反映簧載質量同時存在的垂直振動和俯仰振動以及兩種運動對平順性的影響，與汽車實際存在差距.而汽車四自由度振動平面模型既能反映車身質量的垂直振動和俯仰振動，也能反映前軸和后軸的非簧載質量的垂直振動，是研究輪轂電機電動汽車平順性更合適的模型［21］.

基于上述分析，建立包含輪轂電機的電動汽車四自由度振動平面模型，如圖1所示.

圖1 電動汽車四自由度振動平面模型Fig.1 Four degree-of-freedom vibration plane model of electric vehicle

在圖1 中，ms和IsL分別為簧載質量和簧載俯仰轉動慣量；muf和mur分別為包含電機質量的前軸和后軸的非簧載質量；csf和csr分別為前軸和后軸的懸架阻尼；ksf和ksr分別為前軸和后軸的懸架剛度；ktf和ktr分別為前軸和后軸的輪胎剛度；Lf和Lr分別為簧載質量質心與前軸和后軸的距離；Fvf和Fvr分別為前軸和后軸的電機垂向激勵；Faf和Far分別為前軸和后軸的懸架控制力；zs和φs分別為簧載質量的垂向位移和俯仰角位移；zsf和zsr分別為前軸和后軸的懸架與簧載質量連接點垂向位移；zuf和zur分別為前軸和后軸的非簧載質量垂向位移.

1.4 微分方程

針對zsf、zsr、zuf和zur，由Lagrange 方程建立4 個自由度的微分方程如下：

1.5 狀態(tài)方程

由可控性定理［18］，上述狀態(tài)方程可以實現(xiàn)主動懸架控制.此外，當u(t)=0 時，上述狀態(tài)方程也適用于考慮被動懸架的輪轂電機電動汽車.

2 約束狀態(tài)反饋H∞控制方法

2.1 線性矩陣不等式及其求解

線性矩陣不等式F(x) ＜0，表示對于任意n維非零向量u，uTF(x)u＜0.F(x)的具體表示如下：

成立，或者無解.

2.2 約束狀態(tài)反饋H∞控制

考慮如下表示：

式中：zu（t）為e維控制輸出向量；z（t）為f維約束輸出向量，受到max|z(t)|2＜的約束限制；C1、D1、C2和D2為相應的矩陣.狀態(tài)反饋控制方程為：

式中：K為狀態(tài)反饋增益矩陣.

約束狀態(tài)反饋H∞控制問題，可以描述為：對于給定常數γ＞0，求使得閉環(huán)系統(tǒng)穩(wěn)定的狀態(tài)反饋控制方程.對應式（12）第一個方程和第二個方程，有

對應式（12）第三個方程的約束max|z（t）|2＜由Schur補定理［18］，可以推導出

式中：Q=P-1；N=KQ；ρ=γ2wmax；wmax=maxw(t).

通過式（14）和式（15），約束狀態(tài)反饋H∞控制問題轉化為線性矩陣不等式求解問題.在已知A、B1、B2、C1、D1、C2、D2和γ的條件下，其求解過程為：首先，求解式（14）和式（15）表示的線性矩陣不等式得到Q和N；其次，由Q和N確定K=NQ-1，將u（t）=Kx（t）代入式（12）第一個方程求解，得到約束狀態(tài)反饋H∞控制的狀態(tài)向量x（t）；最后，由式（12）后兩個方程得到控制輸出向量zu（t）和約束輸出向量z（t）.

應當說明的是，式（15）是對應于一個約束輸出向量z(t)的線性矩陣不等式；當存在多個約束輸出向量時，需要依次列出對應于多個約束輸出向量的線性矩陣不等式.

3 主動懸架狀態(tài)反饋H∞控制設計

3.1 控制輸出向量

3.2 約束輸出向量

前懸架和后懸架的動行程超過其最大值z1max和z2max時，懸架就會撞擊限位塊而產生振動和噪聲.為了避免這種現(xiàn)象，需要

汽車行駛時，只有當車輪動載荷小于車輪靜載荷時，才能始終保持車輪接地性和車輛穩(wěn)定性，即

設z2(t)=[zsf-zuf，zsr-zur，zuf-qf，zur-qr]T，聯(lián)立式（17）和式（18），得到對應于懸架動行程和車輪載荷的約束輸出向量：

為了減少控制過程的能量消耗，應當限制懸架控制力在一定范圍內［22］

式中：Fafmax和Farmax分別為前懸架和后懸架的最大控制力.

由式（20）得到控制力約束輸出向量：

3.3 狀態(tài)反饋H∞控制策略

聯(lián)立式（9）、式（16）、式（19）和式（21），輪轂電機電動汽車主動懸架控制問題表示為：

式（22）表示的狀態(tài)反饋H∞控制問題，可以理解為：在外界擾動向量w(t)存在最大值wmax的情況下，如果Q、N和ρ=wmaxγ2滿足如下線性矩陣不等式

則主動懸架的狀態(tài)反饋H∞控制策略為：

4 應用分析

4.1 狀態(tài)反饋H∞控制仿真模型

基于上述理論研究結果開發(fā)了電動汽車脈沖路面狀態(tài)反饋H∞控制MATALB∕Simulink 仿真模型，如圖2 所示.圖2 中，bump 模塊用于生成前輪和后輪的脈沖激勵；Motor Excitation 模塊用于生成前輪和后輪的輪轂電機激勵；State Function 模塊用于生成狀態(tài)方程、控制輸出向量、約束輸出向量的矩陣，以及獲得狀態(tài)反饋增益矩陣；Output Function 用于獲得每個車速下各個振動響應量的時間歷程和各個振動響應量的絕對值最大值，all_data_bump 模塊用于以數據和圖形兩種形式輸出所有結果.仿真時，采用某電動汽車的基本參數，如表1 所示.約束條件設定為：z1max=z2max=0.1m，F(xiàn)afmax=Farmax=1 500 N.

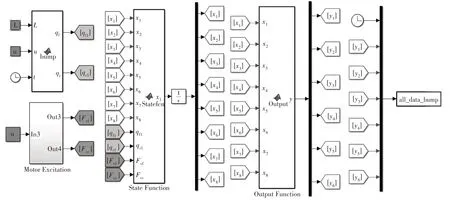
圖2 電動汽車脈沖路面狀態(tài)反饋H∞控制MATALB∕Simulink仿真模型Fig.2 MATALB∕Simulink simulation model of electric vehicle for state feedback H∞control of pulse road

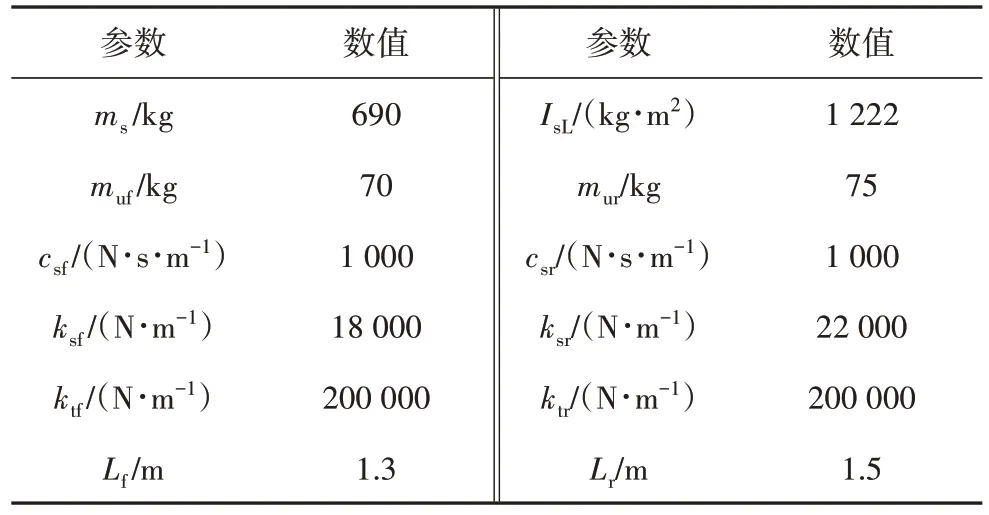
表1 電動汽車基本參數Tab.1 Basic parameters of a electric vehicle

4.2 輪轂電機激勵分析

設偏心距e=(R-r)er，er是以百分率表示的偏心率，分別取er=0%、er=10%和er=20%，前者對應于電機無偏心情況，后者對應于2 種電機偏心情況.取某開關磁阻電機參數見文獻［13］，3 種情況的電機偏心激勵如圖3所示.

由圖3（a）可知，在電機無偏心的情況下，由于電機各處氣隙相同，因此電機不存在垂向激勵.

由圖3（b）和圖3（c）可知，當電機轉子和定子存在偏心時，由于各處氣隙不同，電機產生垂向激勵.進一步分析表明，er取10%以上的偏心率，偏心率越大，產生的電機垂向激勵越大.

圖3 3種情況的輪轂電機激勵Fig.3 Three cases of hub motor excitation

由于小偏心率產生的電機垂向激勵也小，因此，后續(xù)將以偏心率er=10%來研究電機垂向激勵與脈沖路面激勵共同作用，考察電機偏心在脈沖路面下對電動汽車平順性的影響.以此能更好地說明電機偏心對汽車平順性的影響，如果小偏心能產生明顯的影響，則大偏心會產生更大的影響.

4.3 振動響應時間歷程

在脈沖路面、車速40 km∕h 和前后電機偏心率10%的情況下，求取得到兩種懸架的簧載質量垂向加速度、簧載質量俯仰角加速度、前懸架動行程、后懸架動行程、前輪相對動載和后輪相對動載的時間歷程，如圖4所示.

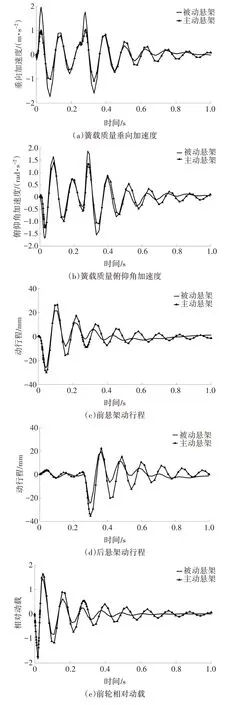
圖4 車速40 km∕h和電機同時偏心10%時脈沖路面振動響應的時間歷程Fig.4 Time history of pulse road vibration response of suspension with 10%motor eccentricity and 40 km∕h

由圖4 可知，主動懸架與被動懸架對比，簧載質量垂向加速度和簧載質量俯仰角加速度最大值得到改善；懸架動行程和車輪相對動載最大值有所增加.

4.4 平順性評價指標的車速特性

振動響應時間歷程用于分析振動響應隨著時間變化的過程，而平順性需要一個反映振動響應的整體指標.GB∕T 4970—2009 規(guī)定，采用振動響應時間歷程的絕對值最大值作為脈沖路面平順性評價指標，并且通過其與車速的關系評價汽車平順性.

取最低車速10 km∕h、車速增量2 km∕h 和最高60 km∕h，在脈沖路面上仿真1 s，設定4 種懸架情況：1）無偏心被動，對應于前后電機無偏心的被動懸架；2）無偏心主動，對應于前后電機無偏心的主動懸架；3）偏心被動，對應于前后電機偏心10%的被動懸架；4）偏心主動，對應于前后電機偏心10%的主動懸架.

針對1 種情況，首先，求解得到1 個車速對應的振動響應時間歷程；其次，求解得到該車速對應的振動響應絕對值最大值；再次，求解得到各個車速對應的振動響應的絕對值最大值；最后，求解得到4 種情況的全部結果，如圖5所示.

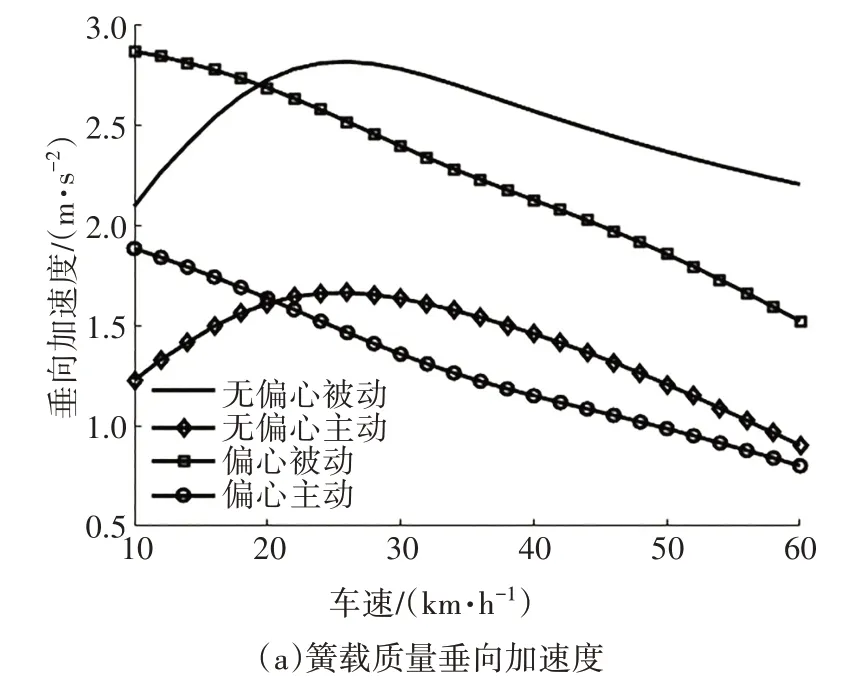
圖5 4種情況的脈沖路面平順性評價指標Fig.5 Evaluation indexes of pulse road ride comfort under four conditions

由圖5 可知，當電機無偏心時，主動懸架與被動懸架對比結果如下：1）簧載質量垂向加速度對比改善44.11%，平均改善1.132 9 m∕s2；2）簧載質量俯仰角加速度對比改善28.50%，平均改善0.622 rad∕s2；3）前懸架動行程對比增加0.09%，平均增加3.06 mm，后懸架動行程對比增加0.07%，平均增加1.99 mm；4）前輪相對動載對比增加7.77%，平均增加0.133 3，后懸架相對動載對比增加5.09%，平均增加0.081 0.當電機偏心10%時，主動懸架與被動懸架對比結果如下：1）簧載質量垂向加速度對比改善42.82%，平均改善0.969 6 m∕s2；2）簧載質量俯仰角加速度對比改善22.41%，平均改善0.449 9 rad∕s2；3）前懸架動行程對比增加14.72%，平均增加4.596 5 mm；后懸架動行程對比增加17.22%，平均增加4.402 5 mm；4）前輪相對動載對比增加14.72%，平均增加0.119 9；后輪相對動載對比增加14.72%，平均增加0.118 4.

5 結論

1）考慮脈沖路面激勵和輪轂電機激勵，建立了輪轂電機電動汽車四自由度振動平面模型，既可以用于分析主動懸架的控制效果，也可以分析被動懸架的作用，適用于研究各種控制方法.

2）總結和說明了可以應用MATLAB 工具箱LMI求解的狀態(tài)反饋H∞控制問題，實現(xiàn)了輪轂電機電動汽車懸架狀態(tài)反饋H∞控制設計，開發(fā)了相應的MATLAB∕Simulink 仿真模型，通過參數設置可以研究單獨脈沖路面車輪激勵作用、單獨電機激勵作用、脈沖路面車輪和電機兩種激勵共同作用的效果.

3）在脈沖路面上，輪轂電機電動汽車主動懸架H∞控制改善了簧載質量垂向加速度和簧載質量俯仰角加速度，增加了前懸架動行程、后懸架動行程、前輪相對動載和后輪相對動載，增加程度都在約束范圍內；電機無偏心和偏心的主動懸架對比說明，偏心影響了主動懸架的改善能力，主動懸架設計需要考慮電機偏心情況.