基于AUPF 算法的水下履帶車動力學參數估計

陳昱衡，吳鴻云，邊有鋼?

（1.湖南大學汽車車身先進設計制造國家重點實驗室，湖南長沙 410082；2.長沙礦山研究院有限責任公司，湖南長沙 410012；3.國家金屬采礦工程技術研究中心，湖南長沙 410012）

位于4～6 km 水深的深海底，其表層沉積物中以半埋藏狀態覆存著大量的多金屬結核礦產資源，因其富含錳、銅、鈷、鎳等稀貴金屬元素，極具商業開采價值.20 世紀70 年代，以美國為首的西方發達國家率先開始深海采礦技術研究，完成了不同程度的試驗，催發了一輪深海采礦技術研究熱潮［1］.

在深海采礦作業時，采礦車沿著預設軌跡進行自行式采集結核，需要在線獲取采礦車的動力學參數.然而，多金屬結核礦區表層含水量高，承載力弱，易流動且伴隨有海底不規則洋流的影響，導致多金屬結核采礦車易發生履帶沉陷和履帶不規則打滑的現象［2］，故履帶沉陷時采礦車的有效驅動輪半徑應考慮履帶板厚度和未陷入底質的驅動輪部分.若忽略驅動輪半徑變化時履帶打滑的動態響應，可能會對控制性能產生負面影響.因此，精準的履帶打滑率和有效驅動輪半徑等運動學參數估計顯得尤為重要.

為解決上述問題，文獻［3-6］基于RecurDyn 參數化建模技術，構建了多剛體深海采礦系統，完成了聯動仿真分析，并對多金屬結核采礦車的直行、差速轉向、爬坡和越障等工況時的機械特性進行了仿真分析，并基于模型車進行試驗以驗證方案的可行性，為深海采礦系統的整體集成設計、性能預測及作業操控提供了參考，同時為多金屬結核采礦車整車機械結構的優化設計提供了理論支撐［7-9］.

無跡卡爾曼濾波（Unscented Kalman Filter，UKF）算法通過無跡變換（Unscented Transformation，UT）將非線性函數模擬成真實分布的近似高斯分布，具有3 階的泰勒精度，是一種易實現的參數估計算法［10-12］.周兵等［13］基于UKF 對非線性輪胎模型中的路面附著系數進行了在線估計，提高了自動駕駛車輛的主動轉向控制性能.Qin 等［14］基于瞬時轉向中心變化的履帶車運動學模型，提出了一種改進的UKF 算法，實現了陸地自行式履帶車輛履帶打滑率的精準在線估計.

本文從多金屬結核采礦車的受力分析出發，建立底盤液壓驅動系統與履帶負載特性的動力學關系，提出了多金屬結核采礦車的有效驅動輪半徑和履帶打滑率等動力學參數的狀態空間模型.針對UKF 算法無法在高非線性模型中得到較高估計精度的問題［15-16］，采用基于蒙特卡洛采樣原理的自適應無跡粒子濾波（Adaptive Unscented Particle Filter，AUPF）算法進行多金屬結核采礦車的動力學參數在線測算，利用自適應無跡卡爾曼濾波（Adaptive Unscented Kalman Filter，AUKF）算法改進概率密度函數以指導粒子濾波（particle filter，PF）進行重要性采樣，克服了粒子濾波易發散的缺點［17］.試驗結果表明，所提出的AUPF算法可實現多金屬結核采礦車的動力學參數的精準在線測算.

1 多金屬結核采礦車參數估計建模

1.1 多金屬結核采礦車受力分析

與陸地履帶車不同，多金屬結核采礦車在多金屬結核礦區稀軟的底質上行駛，為了提高多金屬結核采礦車的抓地能力，行走履帶采用三角履齒.多金屬結核采礦車如圖1所示，三角履齒如圖2所示.

圖1 多金屬結核采礦車Fig.1 Polymetallic nodules mining vehicle

圖2 三角履齒Fig.2 Triangular track teeth

在計算采礦車履帶產生的牽引力F時，不僅需要考慮履帶對底質產生的剪切力F1，還需要考慮履齒剪切底質產生的壓力F2.F1和F2分別見式（1）和式（2）.

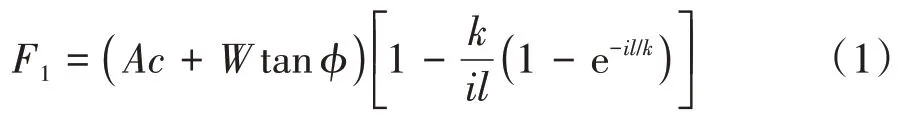
式中：A為履帶的接地面積，m2；W為車身正壓力，N；c為底質內聚壓力，kPa；φ為底質內摩擦角參數，(°)；l為履帶接地長度，m；i為履帶打滑率；k為底質水平剪切模變數，m.

式中：b2為履齒寬度，m；γs為底質比重，kg∕m3；hb為履齒高度，m；Nφ=tan2(45°+0.5φ)為底質流值；n2為履齒個數.

牽引力F為：

1.2 多金屬結核采礦車動力學參數在線測算模型

多金屬采礦車在含水量高的稀軟底質進行自行式作業時，底盤會發生沉陷現象，故實際的履帶有效驅動輪半徑ra為：

式中：r1為履帶板厚度和履齒高度的和，m；r2為測高聲吶測得的履帶沉陷，m；r為理論驅動輪半徑，m.

多金屬采礦車左右履帶驅動采用兩獨立的閉式液壓回路，即采用兩電動機分別驅動兩變量泵，再經過定量馬達傳遞到左右履帶，馬達直接驅動采礦車行走.其中液壓馬達的系統壓力pl與馬達的驅動力矩Tq呈線性關系，如式（5）所示.

式中：VM為液壓馬達的理論弧度流量，m3∕rad；pl為系統壓力，Pa；θm為液壓馬達轉角，rad；Jt為液壓馬達和負載總慣量，m·N·s2；Bm為負載和液壓馬達內部的總黏性阻尼系數，m·N·s∕rad；G為負載的扭矩剛度，m·N∕rad；ωm=dθm∕dt為液壓馬達轉速，rad∕s；ω˙m=dωm∕dt為液壓馬達角加速度，rad∕s2.

多金屬結核采礦車為低速勻速行駛，故在建模時可假設馬達的負載力矩TL等于驅動力矩Tq：

驅動輪由液壓馬達直驅，故驅動輪轉速ω等于液壓馬達轉速ωm：

聯立式（5）～式（7）負載力矩TL與驅動輪轉速ω的方程，如式（8）所示.

同時驅動力矩Tq滿足：

為了簡化運算，基于文獻［18］，對式（1）進行簡化，得

聯立式（2）式、式（4）、式（8）～式（10），可得到履帶有效驅動輪半徑和履帶打滑率的關系.

通過離散化式（4）和式（10），定義如式（12）所示的狀態空間模型.

狀態量為：

控制量為：

觀測量為：

由于采礦車為低速行駛，故較小時間間隔內的平均速度可視為履帶實際速度va.

式中：T為采樣時間，s；L為每個采樣時間T內的履帶行走長度，m.

2 自適應無跡粒子濾波算法

粒子濾波算法不依賴高斯模型，基于蒙特卡羅采樣原理，可應用于高線性系統的參數估計.但是PF 算法存在濾波易發散的缺點，通常采用UKF 算法指導粒子重采樣以改進PF 算法.本文采用AUKF 指導粒子重采樣的AUPF 進行參數估計.AUPF 的算法流程如表1所示.

表1 AUPF算法流程Tab.1 AUPF algorithm flow

AUKF算法的具體步驟如下：

1）初始化.

2）Sigma點權重計算.

式中：λ=n(α2-1)，α是控制Sigma 點分布的常數，其取值范圍為e-4≤α≤1；β為非負常數，將高階成分的信息轉換到方差中，取β=2.

3）Sigma點選擇和估計值更新.在UT中，隨機變量由一組最小的樣本點表示，稱為Sigma 點.計算這些點在非線性系統模型傳播時的后驗平均值和協方差.Sigma點由式（16）計算.

粒子集合XAUPF(k)由式（23）計算.

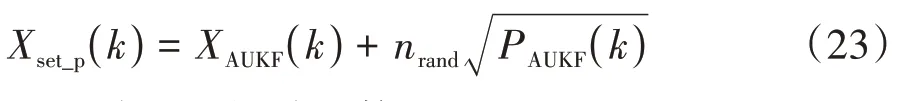
式中：nrand為0～1的隨機數.

粒子權重計算具體步驟如下：

1）計算觀測值YAUPF(k).

2）計算粒子權重并歸一化.

通過設定權重閾值進行重采樣并更新狀態與基本PF算法一致，本文不再贅述，見參考文獻［10］.

基于張滔等人［9］的研究，式（1）、式（2）中多金屬結核底質土力學特性的參數值和采礦車動力學參數測算模型的參數如表2所示.

表2 模型參數值Tab.2 Parameter values of the model

3 動力學參數在線測算方法實驗驗證

為了驗證本文提出的動力學參數測算算法能否精準測算多金屬結核采礦車的履帶打滑率和有效驅動輪半徑，定義如下性能需求：有效驅動輪最大誤差不超過5 mm，履帶打滑率的最大誤差不超過5%.以上述多金屬結核采礦車為實驗對象，在深海采礦實驗水池進行行走實驗，實驗水池長60 m，寬50 m，深5 m，實驗室水池如圖3所示.

圖3 實驗室水池Fig.3 Laboratory sink

水池底質為河泥以模擬多金屬結核礦區的稀軟地形，水深保證可以淹沒整個多金屬結核采礦車.多金屬結核采礦車通過起重機下放至水池中，由慣性導航單元和多普勒測速組成的水下組合導航系統使采礦車完成如圖4所示的行走路線.

圖4 采礦車實驗行走路線Fig.4 Mining vehicle’s test route

測控主系統為美國National Instruments 公司推出的Compact RIO 嵌入式測控平臺及軟件.車載本地測控站采集并記錄采礦車上各傳感器檢測參數，多金屬結核采礦車搭載多普勒測速儀、光纖陀螺、履帶驅動電機編碼器、測高聲吶等傳感器實時獲取采礦車的運動信息.光纖陀螺給出精準的采礦車的航向角φ和角速度ω′；履帶驅動電機編碼器給出采礦車帶驅動輪的轉速ω和加速度ω˙.

車載本地測控站記錄所測算的外側履帶打滑率io、內側履帶打滑率ii、外側有效驅動輪半徑ro和內側有效驅動輪半徑ri的實驗數據分別如表3 和圖5～圖8 所示.同時實際的驅動輪半徑通過式（4）計算，實際打滑率由式（26）計算.

表3 運動參數均方差Tab.3 Mean square error of motion parameters

圖5 外側履帶打滑率Fig.5 Lateral track skid rate

圖6 內側履帶打滑率Fig.6 Medial track skid rate

圖7 外側有效驅動輪半徑Fig.7 Effective radius of the lateral driving wheel

圖8 內側有效驅動輪半徑Fig.8 Effective radius of the medial driving wheel

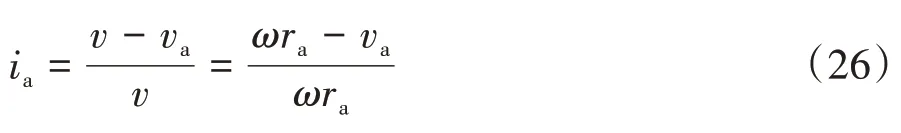
式中：va為履帶實際速度，由式（13）計算.

由實驗結果可知，有效驅動輪半徑的誤差在3 mm 以內，履帶打滑率的最大誤差不超過5%，有效驅動輪半徑的誤差均方差小于0.5，履帶打滑率誤差均方差小于1.5.

誤差的產生可能是由于實驗室模擬底質的力學特性與真實底質的力學特性有一定的差距，故狀態空間模型中的底質力學特性與實驗水池模擬底質的力學特性存在不匹配的情況.但是有效驅動輪半徑的誤差和履帶打滑誤差都小于最大誤差，且均方差均較低.通過AUPF 算法可以得到精度較高的多金屬結核采礦車動力學參數，同時說明AUPF算法對模型的不匹配情況也具有較好的適應性.

4 總結

針對多金屬結核采礦車在海底行駛作業時，履帶打滑率和有效驅動輪半徑等動力學參數難以確定的問題，本文通過分析多金屬結核采礦車的履帶牽引力和履帶的液壓負載特性，建立了多金屬結核采礦車履帶打滑率和有效驅動輪半徑等動力學參數在線測算的狀態空間模型.針對動力學參數測算狀態空間模型非線性程度較高的問題，提出了利用AUPF算法進行多金屬結核采礦車動力學參數測算的方案.實驗結果表明，有效驅動輪半徑的誤差控制在3 mm 以內，打滑率的最大誤差不超過5%，滿足動力學參數測算的精度要求，驗證了所提方案的可行性，具有重要的工程應用價值.