雙圓弧諧波剛輪刮齒加工原理及刀具設計

莫帥，王賽賽，羅炳睿，岑國建

（1.天津工業大學機械工程學院，天津 300387；2.天津市現代機電裝備技術重點實驗室，天津 300387；3.寧波中大力德智能傳動股份有限公司，浙江寧波 315301；4.江蘇萬基傳動科技有限公司，江蘇泰州 225400）

在諧波傳動中，齒輪的齒形設計及加工工藝對其傳動特性有較大影響.隨著科學技術的發展，國內外學者對諧波齒輪做了大量分析研究［1-4］，辛洪兵［1］和王家序等［4］指出雙圓弧齒形的諧波減速器具有良好的傳動質量.由于齒形復雜，諧波齒輪制造工藝受到極大限制，王仕璞等［3］提出以具有正前角的滾刀加工諧波柔輪，并建立刀具模型；Yoshino等［5］根據單元去除理論提出一種特殊齒形齒輪的插齒刀具設計方法.刮齒作為一種新型齒輪加工技術具有比插齒更高的精度和效率.目前，國內關于刮齒刀具設計方法的研究成果較少［6-15］，其中賈康等［7］基于展成加工原理，給出一種由刮齒前刀面與離散曲面相交構建切削刃的方法；Guo等［9］提出一種無理論誤差直齒刮齒刀具結構，并建立數學模型，為刮齒刀具參數優化提供參考.

刮齒加工技術尚未應用到諧波齒輪的加工中.本文以偏離端面一定角度的平面作為前刀面，設計適應雙圓弧齒形諧波剛輪加工的刮齒刀具模型，降低刀具加工和磨削難度，使工件具有較小的刃形誤差，提高雙圓弧諧波剛輪的加工精度和效率.

1 刮齒加工原理

刮齒加工方式與插齒類似，都是基于展成加工原理，區別在于切削的作用方式不同.插齒加工時工件和刀具做無間隙嚙合運動，同時插齒刀沿工件軸向做往復切削運動.刮齒加工示意圖如圖1所示，工件與刀具保持恒定的軸交角，同時做旋轉嚙合運動和軸向進給運動，工件和刀具由于強制嚙合而產生一系列微小溝壑，構成工件曲面.在機床作用下刀具沿徑向推進，最終完成齒輪的加工［9］.

圖1 刮齒加工示意圖Fig.1 Machining diagram of gear skiving

2 諧波齒輪齒廓設計方法

2.1 雙圓弧諧波柔輪齒廓方程

雙圓弧諧波柔輪齒廓如圖2 所示，其基準形式為圓弧-公切線-圓弧.建立柔輪齒廓坐標系XOY，圓弧段圓心坐標Oa（xa，ya）、Ob（xb，yb），其中xa=-ca，ya=ha+hf+da-la，xb=πm/2+cb，yb=hf+da+lb.以柔輪單側齒廓為例，各參數取值如表1 所示，表中ra和rb分別為凸圓弧和凹圓弧半徑，δ為公切線傾角，lf為公切線豎直距離，α為OaB與水平方向的夾角.以齒廓弧長s為變量，建立公切線雙圓弧諧波柔輪的凸段齒廓、切線段齒廓和凹段齒廓的分段方程.

圖2 諧波柔輪齒廓坐標系Fig.2 Harmonic flexible tooth profile coordinate system

表1 柔輪基本設計參數Tab.1 Design parameters of flexspline

諧波柔輪凸圓弧BC段齒廓方程為：

諧波柔輪公切線CD段齒廓方程為：

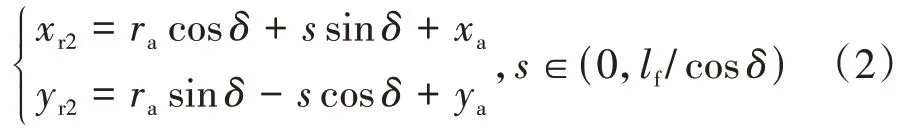
諧波柔輪凹圓弧DE段齒廓方程為：

式中：l1=rb{π∕2 -arccos[(lb+hf)∕2]-δ}-cb.

2.2 剛輪齒廓方程求解

諧波齒輪傳動過程中，柔輪因為波發生器的作用而發生變形，因此常用包絡法求解諧波剛輪齒廓［10］.圖3為諧波齒輪傳動坐標系，在圖3中，當柔輪在諧波發生器的作用下沿原始曲線Cl運動時，齒廓曲線Rl的包絡即為所求剛輪齒廓Gl.

圖3 諧波齒輪傳動坐標系Fig.3 Harmonic gear drive coordinate system

諧波齒輪傳動的基本設計參數如表2 所示.其中柔輪徑向最大變形量w0取0.5 mm，設柔輪和剛輪齒廓坐標分別為（xr，yr）、（xg，yg）.

表2 諧波齒輪傳動基本設計參數Tab.2 Basic design parameters of harmonic drive

方程（4）為諧波柔輪齒廓坐標系向剛輪齒廓坐標系的轉換方程，式中包含未知變量φ與s.諧波齒輪在傳動嚙合過程中滿足嚙合方程（5），選取并離散s值，代入式（5）可求出對應的φ值.將求解得到的φ與s代入式（4），可得到剛輪齒廓坐標.

圖4 通過坐標變換模擬柔輪與剛輪的相對運動，直觀反映出諧波齒輪傳動的嚙合特征，剛輪齒廓在柔輪的包絡中得到正確驗證.

圖4 諧波剛輪包絡齒廓Fig.4 Envelope tooth profile of harmonic rigid wheel

為便于圖4 的工藝實現，對剛輪齒廓公切線段以直線y=kx+b擬合，對圓弧段以圓形方程（6）擬合.

設剛輪齒廓點（xi，yi），令y=f（x，tj），j=1，2，…，m.取精度為0.000 1，p（tj）滿足式（7），各常數滿足式（8）.

將齒廓離散坐標點代入擬合公式，可得剛輪凸、凹圓弧段圓心坐標分別為Og1（0.139 1，0.332 5）和Og2（0.338 8，0.582 2）；半徑分別為r1=0.693 7、r2=0.759 9；公切線段分別為k=-7.840 1、b=28.507 7.設齒廓方程為F（x，y），在z方向離散可得剛輪齒面坐標點云如圖5 所示.工件齒面上任意點法失N的分量分別為：

圖5 諧波剛輪齒面坐標點云Fig.5 Harmonic rigid tooth surface coordinate point cloud

3 剛輪刮齒刀具幾何參數計算

刮齒刀具與其他齒輪加工刀具類似，都具有切削刃和前后刀面等結構要素［11］.刮齒刀具結構如圖6所示.

圖6 刮齒刀具結構圖Fig.6 Picture of skiving cutter structure

3.1 前刀面數學模型

在刮齒加工中，刀具與工件之間存在軸交角，因此采用與端面一定角度的平面作為前刀面，使刮齒刀具兩側刃切削角度相近，減小刃形誤差［12］.

圖7 為刮齒刀具前刀面坐標系.在圖7 中，坐標系XYZ為前刀面坐標系，XaYaZa為輔助面坐標系，X2Y2Z2為刀具運動坐標系.前刀面法向量在坐標系XYZ中可表示為n（0，0，1），根據式（10）可得，在刀具運動坐標系中的前刀面法向量為n1（sinαcosβ，sinβ，cosβcosα）.

圖7 刮齒刀具前刀面坐標系Fig.7 Skiving cutter rake face coordinate system

式中：B1為前刀面向輔助面變換的矩陣；B2為輔助面向刀具運動坐標系變換的矩陣.

在X2Y2Z2坐標系中前刀面方程為：

3.2 共軛面數學模型

3.2.1 相對運動速度

刮齒加工坐標系如圖8 所示.S1-O1X1Y1Z1為工件坐標系，S2-O2X2Y2Z2為刀具坐標系，S0-O0X0Y0Z0和SP-OPXPYPZP為參考坐標系，i、j、k和ip、jp、kp分別為坐標系S0和SP對應坐標軸的單位向量.加工運動時刀具以w2轉動并沿z1軸負方向移動，工件以w1定軸轉動，共軛面與刀具齒面在M點共軛.

圖8 刮齒加工坐標系Fig.8 Machining coordinate system of gear skiving

S0和SP的位置關系為：

共軛點M在坐標系SP中滿足式（15）：

解得v12在SP中的分量為：

式中：β1和β2分別為工件和刀具螺旋角；n1和n2分別為工件和刀具齒數；m為模數.

式中：Mp1為S1向SP的變換矩陣.

3.2.2 共軛關系

共軛點在嚙合運動時滿足嚙合原理［13］.

將式（9）、式（16）代入式（21），可解得S1繞Zp轉過的角度θ1.齒面在M點嚙合時滿足：

整理得共軛面坐標點為：

三次B 樣條曲面（Non-Uniform Rational BSplines，NURBS）具有良好的局部性質［14-15］.為便于切削刃的求解，將共軛面擬合，在其上選取K×L個型值點，設參數u方向為Fi，j.

根據自由端點條件（27）可求得u向控制點Vi，j，將其作為w方向的型值點，以同樣的方法求出B 樣條曲面控制點pi，j.當參數u和w掃過它的整個定義域時，等參數線描述成如圖9所示擬合曲面.

圖9 共軛面擬合點云Fig.9 The point cloud of conjugate surface fitting

B樣條曲面擬合方程如式（28）所示.

3.3 主刃和主后刀面模型

共軛面經三次B樣條曲面擬合，其中x2=P1（u，w）、y2=P2（u，w）、z2=P3（u，w）.

前刀面方程為：

f（x2，y2，z2）=0

x2、y2和z2關系如式（13）所示.共軛面與前刀面交線方程為：

f（P1（u，w），P2（u，w），P3（u，w））=P（u，w）=0

本文采用牛頓迭代法逼近共軛面，擬合點云與等值線P（u，w）=0的距離，獲得主切削刃.

將u、w均分為n份，擬合后的共軛面上每一個網格間距為Δu=Δw=1/n，矩形單元Δij的4 個頂點與前刀面交線方程對應函數值分別為P（ui，wj）、P（ui，wj+1）、P（ui+1，wj）、P（ui+1，wj+1）.主切削刃的求取就是計算共軛面網格單元邊與P（u，w）=0的交點，具體步驟如下：

1）將擬合后的共軛面點云代入交線方程并判斷每個網格頂點的符號（大于0 記為“+”，否則記為“-”）.

2）若共軛面網格單元的頂點符號相同，則與等值線P（u，v）=0無交點，否則轉到3）.

3）對于兩端異號的單元邊，采用牛頓迭代計算交點，對于單元邊wj-wj+1，設P（ui+1，wj+1）為“-”，P（ui+1，wj）為“+”，交點（ut，wt）中ut=ui+1，wt利用牛頓迭代公式（11）求取.

令w1=wj、w2=wj+1，設置迭代精度ξ=0.001，迭代至wk+1-wk＜ξ時wt=wk+1.求出對應的u、w值代入x2、y2和z2，可獲得交點如圖10所示.

圖10 曲面求交示意圖Fig.10 Schematic diagram of intersection

當刀具刃磨后，前刀面在刀具運動坐標系中沿Z2軸方向移動Δb，同時為保證工件全齒高，刀具工件中心距增大Δa，構成一個新的主刃，將所有主刃特征點擬合就構成主后刀面.

4 刮齒刀具數字化設計

以雙圓弧諧波剛輪為例，設計刮齒刀具三維模型.工件參數為：模數m=0.5 mm，齒數z1=102，螺旋角β=0，轉速n1=1 000 r∕min.刀具參數為：轉速n2=1 522.4 r∕min，齒數z2=67，速度v=0.1 mm∕r.

刮齒刀具設計流程如圖11 所示.參照3.1 節內容求得前刀面方程；根據工件參數按照3.2節內容建立齒面方程.設γ=5°，計算得到共軛面坐標點云，并用三次B 樣條曲面擬合；根據3.3 節內容，設初始中心距a=8.75 mm，改變交點參數Δa=0.1 mm，Δb=2 mm，部分交點坐標數據如表3所示.利用式（30）擬合交點即得到切削刃.

表3 交點坐標數據Tab.3 Intersecting point coordinates data mm

圖11 刮齒刀具設計流程圖Fig.11 Design process of skiving cutter

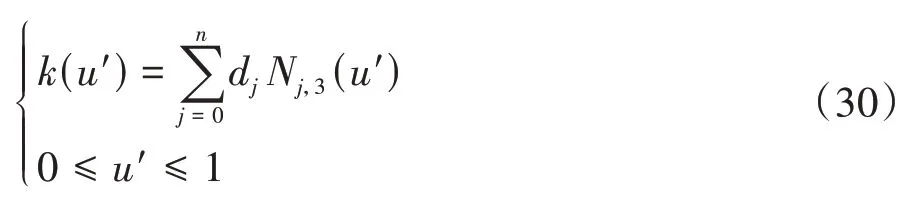
將B樣條曲線擬合后的切削刃點云導入CAD 軟件中構建刮齒刀齒面，通過曲面縫合構建單齒模型，將單齒實體陣列獲得刮齒刀具實體模型，如圖12所示.

圖12 刮齒刀具實體模型Fig.12 Solid model of skiving cutter

5 刮齒刀具齒廓誤差分析

在《圓柱齒輪精度制第1部分：輪齒同側齒面偏差的定義和允許值》（GB∕T 10095.1—2008）中，將漸開線齒廓誤差定義為實際齒廓偏離設計齒廓的量，該量在端平面內且垂直于漸開線齒廓的方向.區別于漸開線，雙圓弧齒廓刀具齒廓偏差Δf可看作齒廓對應點在其半徑方向與偏移齒廓的距離.圖13 為齒廓誤差示意圖.圖13（b）中刮齒刀具剖面Ⅰ-Ⅰ端面齒廓對應圖13（a）中標準齒廓a，Ⅱ-Ⅱ端面齒廓對應標準齒廓b.齒廓b為齒廓a的變位齒廓，標準齒廓凸圓弧段點坐標為（x1，y1），對應齒廓b 上坐標（x2，y2），圓心Oa2對應坐標（xoa2，yoa2）.以凸圓弧段為例，將齒廓b繞圓心Oa2逆時針旋轉Δθ得到齒廓3.在雙圓弧齒廓中忽略長度較小的公切線段，根據位置轉換關系可知，對應弧長s的點齒廓偏差Δf如式（32）所示，其中Δθ可根據B1、B2和圓心Oa1的坐標求得.

圖13 齒廓誤差示意圖Fig.13 Schematic diagram of tooth profile error

在實際齒廓中，由于前后角的存在，刮齒刀具切削刃上任意點對應端面齒廓變位量Δa不同，其關系如式（33）所示，其中Δl為弧長s對應點與齒廓頂點的垂直距離.將刀具刃磨參數代入齒廓誤差計算公式，可得切削刃上任意點齒廓偏差如圖14 所示.刮齒刀具側刃齒廓偏差隨弧長s的增大而增大，最大齒廓偏差約為3 μm.

圖14 刮齒刀具齒廓偏差Fig.14 Skiving cutter tooth profile error

改變頂刃后角和前角，取側刃最大誤差值對應點計算前后角對齒廓最大誤差的影響，如圖15 所示.由圖15 可知，最大誤差隨前后角增大而增大，在對應范圍內，最大齒廓誤差小于15 μm.在實際切削過程中，雖然較小的前角和后角能有效降低齒廓誤差，但也會影響切削效率和刀具壽命.

圖15 刮齒刀具不同前后角對應齒廓誤差Fig.15 Skiving cutter tooth profile error corresponding to different front and back angles

6 結論

1）提出一種諧波齒輪新型加工方法，根據曲面展成原理，通過改變傳統加工刀具切削刃與切削的作用位置，設計加工精度和效率更高的刮齒刀具加工諧波剛輪，優化了其加工工藝.

2）根據諧波傳動特性求解并擬合剛輪齒廓；由嚙合原理和刮齒刀結構特點構建坐標系，求解并擬合共軛面和前刀面模型；將前刀面與共軛面求交并擬合獲取切削刃數據，導入CAD 軟件建立刮齒刀具數學模型.

3）該雙圓弧齒廓刮齒刀具設計及對應齒廓誤差計算方法，具有一定的通用性，進一步完善了刮齒刀具設計理論，可為其他雙圓弧齒廓齒輪加工刀具設計、誤差分析及修形等提供參考.