SA-BP神經(jīng)網(wǎng)絡(luò)在滑坡位移預(yù)測(cè)中的應(yīng)用研究

張文杰

（安徽水安建設(shè)集團(tuán)股份有限公司 合肥 230001）

1 引言

我國(guó)是世界上遭受自然災(zāi)害最為嚴(yán)重的國(guó)家之一，自20世紀(jì)80年代以來(lái)，隨著經(jīng)濟(jì)的快速發(fā)展，人類的工程活動(dòng)日益頻繁，在多種自然因素的影響下使得滑坡災(zāi)害成為各類災(zāi)害中頻率最高、危害性最強(qiáng)的地質(zhì)災(zāi)害類型，且具有逐年加劇趨勢(shì)。因此，如何精準(zhǔn)和有效預(yù)防滑坡災(zāi)害已成為該研究領(lǐng)域的熱點(diǎn)。

近年來(lái)，滑坡位移預(yù)測(cè)逐漸成為滑坡預(yù)警的有效手段之一，它允許研究人員在滑坡位移監(jiān)測(cè)數(shù)據(jù)分析的基礎(chǔ)上，采用相關(guān)數(shù)學(xué)模型進(jìn)行擬合，從而能更加精準(zhǔn)地進(jìn)行滑坡位移預(yù)測(cè)。由于這種方法易于實(shí)現(xiàn)并且精度較高，因此得到了迅速發(fā)展。目前，已有很多關(guān)于滑坡位移預(yù)測(cè)的智能算法研究，如BP神經(jīng)網(wǎng)絡(luò)、支持向量機(jī)、灰色模型等。

鑒于僅通過(guò)單一模型進(jìn)行滑坡預(yù)測(cè)具有局限性，有學(xué)者嘗試將多個(gè)模型組合起來(lái)共同進(jìn)行滑坡預(yù)測(cè)，提出了混合預(yù)測(cè)法。本文則采用模擬退火算法（SimulatedAnnealing，SA）與BP 神經(jīng)網(wǎng)絡(luò)相結(jié)合的混合模型對(duì)某實(shí)例邊坡位移進(jìn)行預(yù)測(cè)，算例結(jié)果證明了本文所提出方法的有效性。

2 SA-BP 神經(jīng)網(wǎng)絡(luò)算法

2.1 SA 算法

模擬退火算法（SimulatedAnnealing，SA）是于1953年由N.Metropolis 等人提出，它是基于Monte-Carlo 迭代求解策略的一種隨機(jī)尋優(yōu)算法，由Metropolis 算法和退火過(guò)程兩部分組成。其基本思想是模擬物理學(xué)中固體物質(zhì)的退火過(guò)程，當(dāng)溫度升高時(shí)，固體內(nèi)部的分子做無(wú)序運(yùn)動(dòng)，內(nèi)能增大；隨著溫度降低，分子逐漸從無(wú)序運(yùn)動(dòng)趨向于有序運(yùn)動(dòng)，內(nèi)能降低；在溫度下降時(shí)對(duì)于任意給定的溫度，固體物質(zhì)內(nèi)都能夠?qū)崿F(xiàn)熱平衡，此時(shí)可將其看作為局部最優(yōu)解；當(dāng)固體物質(zhì)達(dá)到最低溫度，其內(nèi)能最小，此時(shí)可將熱平衡看作為全局最優(yōu)解。

其基本步驟如下：

（1）初始化：給定初始溫度T=T0，初始解S；

（2）產(chǎn)生新解Snew：Snew=S+△S，其中，△S 為[dmin，dmax]之間的隨機(jī)數(shù)，并計(jì)算：△E=E（Snew）-E（S）；其中E（S）為優(yōu)化目標(biāo)；

（3）如果△E ＜0，則接受Snew為新的當(dāng)前解；否則以概率P=exp （-△E/Ti）接受Snew為新的當(dāng)前解；

（4）重復(fù)（2），（3），直到系統(tǒng)達(dá)到平衡狀態(tài)；

（5）T 逐漸減小，重復(fù)（2）至（4），直至達(dá)到最低溫度，輸出最優(yōu)解。

2.2 BP 神經(jīng)網(wǎng)絡(luò)

BP 神經(jīng)網(wǎng)絡(luò)是1986年由Rumelhart 等提出的一種多層前向反饋神經(jīng)網(wǎng)絡(luò)，通過(guò)模擬人類的大腦結(jié)構(gòu)與功能來(lái)處理多變量問(wèn)題，具有良好的學(xué)習(xí)能力，能夠較好地處理非線性問(wèn)題。基本的BP 神經(jīng)網(wǎng)絡(luò)是由三層拓?fù)浣Y(jié)構(gòu)組成：輸入層、隱藏層和輸出層，其結(jié)構(gòu)形式如圖1 所示。

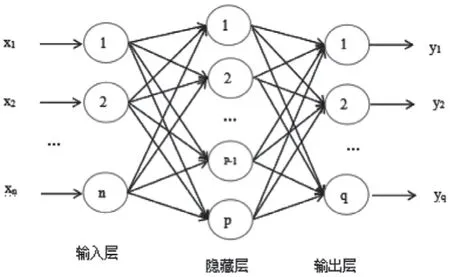
圖1 BP 神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)圖

2.3 SA-BP 神經(jīng)網(wǎng)絡(luò)算法

BP 神經(jīng)網(wǎng)絡(luò)在對(duì)權(quán)值和閾值的迭代調(diào)整過(guò)程中采用梯度下降法，容易使其陷入局部最優(yōu)且收斂速度慢。模擬退火算法具有全局搜索能力和局部尋優(yōu)能力，借助其對(duì)BP 神經(jīng)網(wǎng)絡(luò)進(jìn)行優(yōu)化，將其引入到BP神經(jīng)網(wǎng)絡(luò)的權(quán)值和閾值更新過(guò)程中，使用隨機(jī)擾動(dòng)取代梯度下降法，以解決BP 神經(jīng)網(wǎng)絡(luò)容易出現(xiàn)局部最優(yōu)、收斂慢等問(wèn)題，從而實(shí)現(xiàn)滑坡位移的有效預(yù)測(cè)。其計(jì)算流程如圖2 所示。

圖2 SA-BP 模型流程圖

3 工程實(shí)例

白水河滑坡位于三峽庫(kù)區(qū)長(zhǎng)江寬河谷地段秭歸縣境內(nèi)，距離三峽大壩約56km。滑坡南北向長(zhǎng)約600m，東西向?qū)捈s700m，滑體平均厚度約30m，體積約1260×104m3。該滑坡體為特大型老滑坡松散堆積體，出露地層為下侏羅統(tǒng)香溪群中厚層狀砂巖夾薄層狀泥巖；滑坡后緣高程為410m，以巖土分界處為界，前緣高程約70m，現(xiàn)已沒(méi)入庫(kù)水位以下，東西兩側(cè)以基巖山脊為界，總體坡度約30°；滑坡滑體主要由崩石、坡積物及滑坡堆積物組成，滑帶以含碎石或者含角礫粉質(zhì)黏土為主。自2003年三峽工程蓄水以來(lái)，對(duì)其進(jìn)行了專業(yè)監(jiān)測(cè)。

2007年1月至2012年12月ZG118 站點(diǎn)監(jiān)測(cè)到的水平累計(jì)位移、水位和降雨量數(shù)據(jù)如圖3、圖4所示。可以看出，水庫(kù)水位和降雨量變化是白水河滑坡的主要破壞因素。

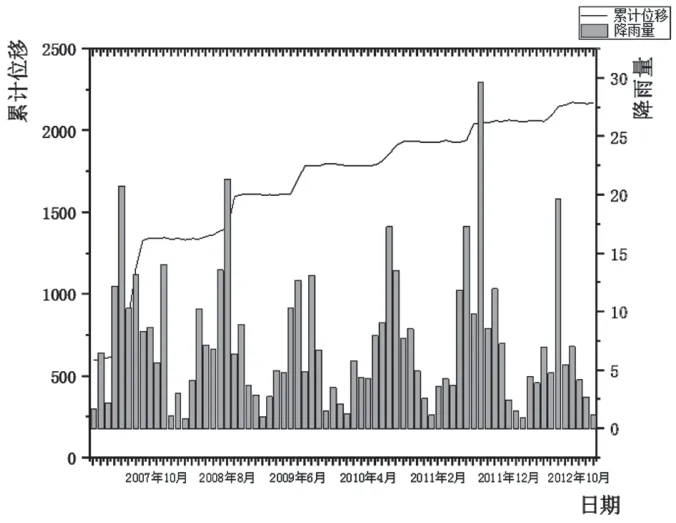
圖3 累計(jì)位移與降雨量曲線圖

圖4 累計(jì)位移與水位曲線圖

選擇監(jiān)測(cè)點(diǎn)ZG118的水平累計(jì)位移為研究對(duì)象，取2007年1月至2012年1月的數(shù)據(jù)作為預(yù)測(cè)模型的訓(xùn)練樣本集，2012年2月至2012年12月的數(shù)據(jù)作為預(yù)測(cè)檢驗(yàn)集。

取單月平均降雨量為降雨因子；月均水位為水位因子；取時(shí)間函數(shù)t 為時(shí)效因子。將三個(gè)影響因子作為輸入，累計(jì)位移作為輸出，進(jìn)行基于SA-BP神經(jīng)網(wǎng)絡(luò)的滑坡位移預(yù)測(cè)分析。

將SA-BP 神經(jīng)網(wǎng)絡(luò)模型與BP 神經(jīng)網(wǎng)絡(luò)模型作對(duì)比，滑坡位移預(yù)測(cè)與監(jiān)測(cè)值如圖5 所示。

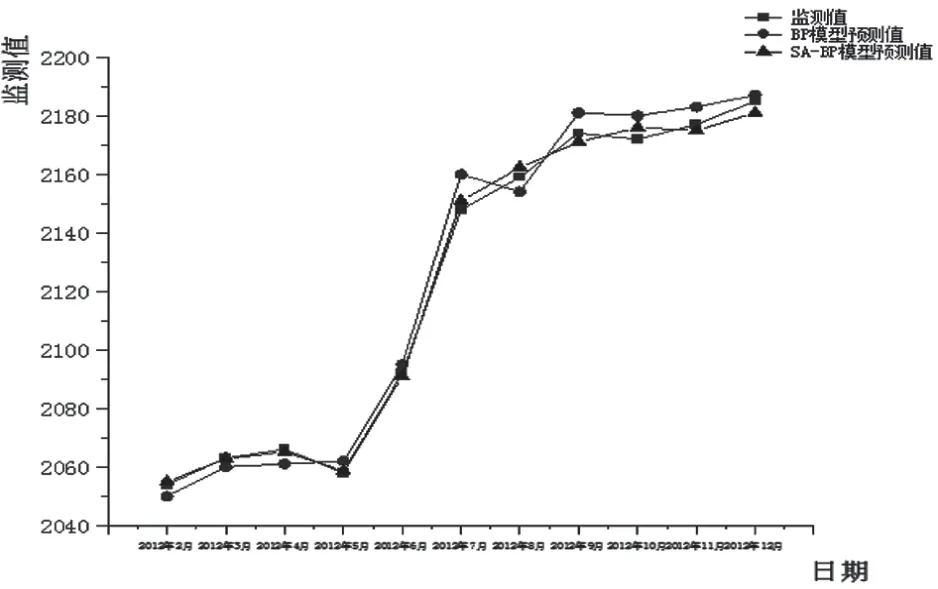
圖5 不同模型的預(yù)測(cè)值與監(jiān)測(cè)值對(duì)比圖

綜合上述分析可知，SA-BP 神經(jīng)網(wǎng)絡(luò)模型對(duì)白水河滑坡的位移預(yù)測(cè)效果比BP 模型要好，其誤差值更低，精度更高。

表1 不同模型預(yù)測(cè)值的誤差值表

4 結(jié)論

本文結(jié)合SA 算法和BP 神經(jīng)網(wǎng)絡(luò)，建立基于SA 算法優(yōu)化BP 神經(jīng)網(wǎng)絡(luò)的滑坡位移預(yù)測(cè)模型。通過(guò)SA 算法優(yōu)化BP 神經(jīng)網(wǎng)絡(luò)的初始連接權(quán)值和閾值，尋找BP 神經(jīng)網(wǎng)絡(luò)的全局最優(yōu)權(quán)值和閾值。將所建立的滑坡位移預(yù)測(cè)模型和傳統(tǒng)BP 神經(jīng)網(wǎng)絡(luò)模型分別應(yīng)用于工程實(shí)例中，結(jié)果表明：SA-BP 神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)邊坡位移誤差較小，具有更高的精度，驗(yàn)證了本文所提出方法的準(zhǔn)確性■