液冷板散熱流道的拓撲優化體積分數研究

劉云飛，熊 敏，丁曉紅

(上海理工大學機械工程學院，上海 200093)

lyfwinder@163.com;xiongmin@usst.edu.cn;dingxh@usst.edu.cn

1 引言(Introduction)

隨著高端制造業、電子芯片業及航空航天領域的發展，對各種散熱技術的散熱能力要求也越來越高，目前常用的散熱技術主要有風冷散熱(自然冷卻和強迫風冷)、液冷散熱和熱管散熱等。相較于風冷散熱，液冷散熱的散熱效率更高；與熱管等氣液相變循環系統相比，單相流體的液冷循環系統也更加簡易穩定。因此，液冷板散熱器廣泛應用于高熱流密度散熱系統中，其中的散熱流道形態是決定液冷板性能的重要因素。傳統的散熱流道設計通常是基于經驗的尺寸優化設計，隨著近年來計算機計算能力的飛速發展，設計自由度高、靈活性強的流體拓撲優化技術已逐漸成為流體傳熱散熱領域的主要設計手段。其方法是將散熱流道設計中需要滿足的各種要求和目標轉化為數學模型，然后選擇適當的尋優算法得到最優解。與傳統的設計方法相比，拓撲優化設計方法更容易確定設計域以明確初始設計方案，且優化求解過程具有明確的數學尋優方向，其設計結果即為滿足設計目標的最優設計，因而可以大大縮短設計周期。而且，隨著以增材制造為代表的先進制造技術的快速發展，過去很難加工的結構，現在也可以高效地制造出來，這也讓拓撲優化設計的結果能更快地轉化為產品。

2 相關研究(Related works)

在散熱流道拓撲優化研究中，KOGA等基于SIMP法，采用序列線性規劃優化算法，將流體功率耗散和換熱量加權相加作為目標函數，研究了不同權重因子：(流體功率耗散：熱交換)、入口邊界條件對液冷通道拓撲形態的影響，并制造了液冷板試樣進行實驗研究。MATSUMORI等通過對參數進行無量綱處理后重新定義積分方程，使流體進口功率恒定，并針對熱載荷與結構相關、不相關兩類優化問題，基于變密度法設計液冷通道形態。李昊等通過流體拓撲優化技術設計了均溫板內部的散熱流道，與傳統流道的液冷板進行對比，并通過實驗驗證了優化后均溫板的優秀散熱性能。本文基于以流固邊界換熱量最大為目標的優化數學模型，對拓撲優化中的體積分數這一關鍵參數進行研究，設計了液冷板模型并依據數值仿真結果對體積分數的最優取值進行分析研究，并給出了由設計參數到設計結果的數學預測模型。

3 基于SIMP法的流體散熱液冷板結構拓撲優化設計(Topology optimization design of liquidcooled plate based on SIMP method)

3.1 流體拓撲優化問題

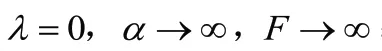
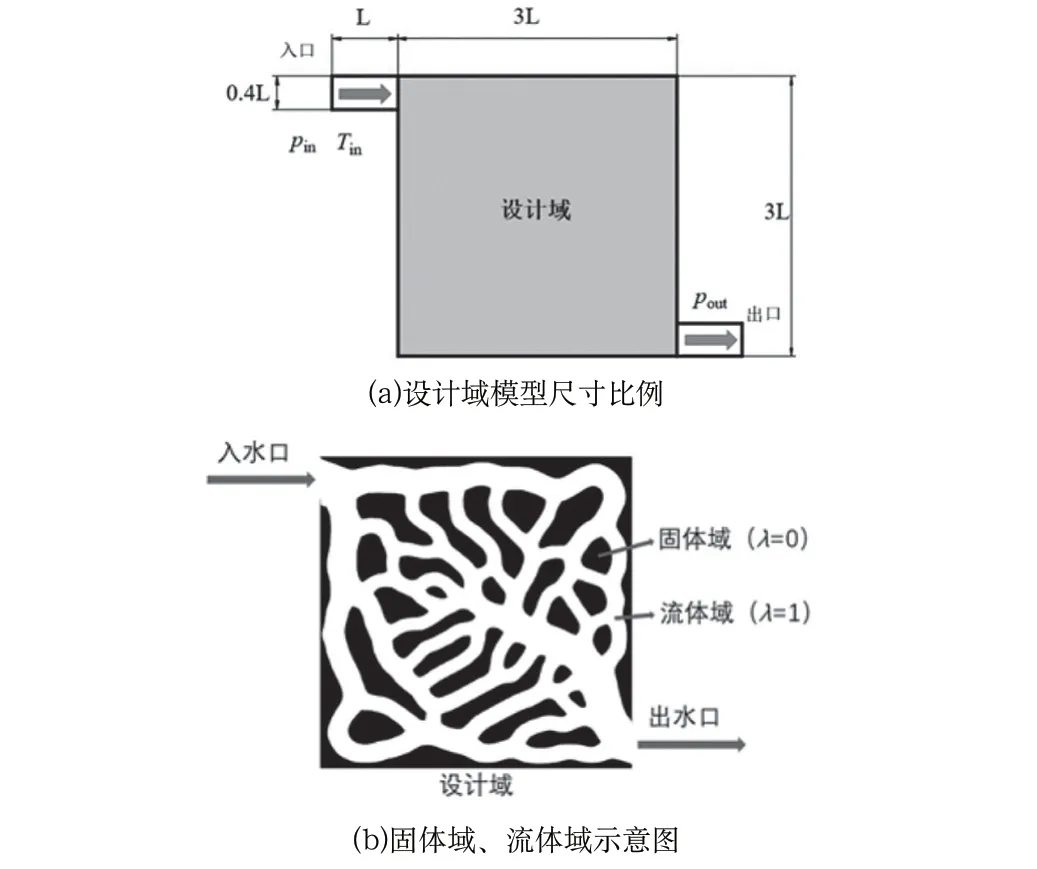
圖1 流體拓撲優化模型示意圖Fig.1 Schematic diagram of fluid topology optimization model

3.2 流體散熱問題

根據LI等對流體拓撲優化中的共軛傳熱研究，針對不可壓縮層流流動，需要滿足連續性方程與動量守恒方程。連續性方程與動量守恒方程的無量綱形式分別通過無量綱速度 u、雷諾數、無量綱壓強、無量綱梯度算子 ?進行定義：

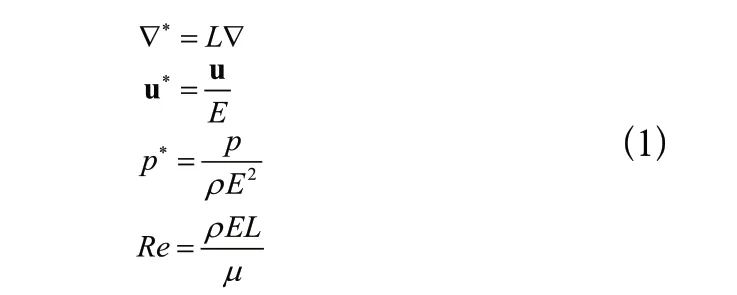
其中，為特征速度，為特征長度，為密度，為動力黏度。

根據達西定律有= -，代入動量守恒方程的體積力及流體域和固體域中能量守恒方程，可分別得到拓撲優化中流場迭代計算方程和溫度場迭代計算方程，如式(2)和式(3)所示[10]：

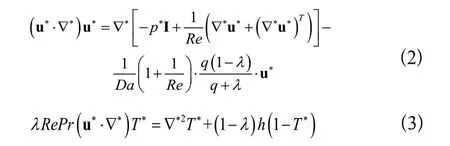
式中，為懲罰因數，本文取0.0 1；為達西數，取0.0001；流體工質為常溫下的液態水，故普朗特數取6.78；流體通道最終拓撲形態與和換熱系數的取值相關，本文以=100，取為300進行拓撲優化設計。由于系統內的熱量最終由流過模型內部的流體帶走，因此以流固邊界換熱量最大為目標的優化數學模型為：

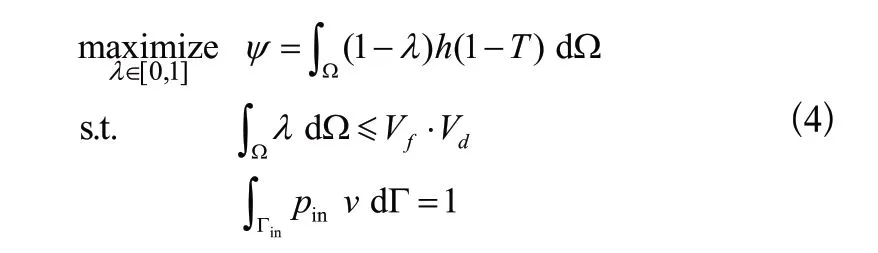
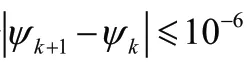
3.3 液冷板拓撲優化設計及散熱性能分析

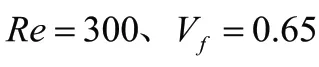
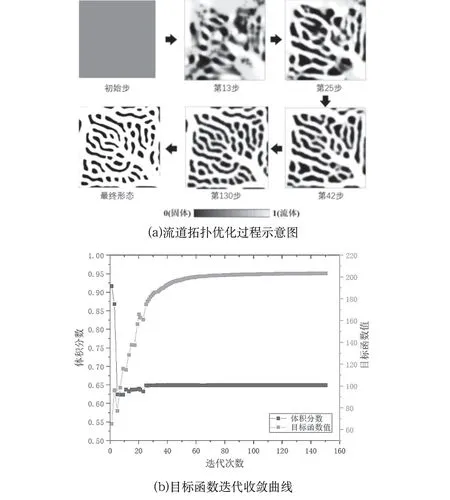
圖2 流道拓撲優化過程及目標函數迭代收斂曲線Fig.2 Process of passage topology optimization and iterative convergence curve of the objective function

將得到的流道邊界使用霍爾姆茲偏微分方程形式的密度過濾，再進行雙曲正切投影過濾，得到清晰的流道邊界。而后進行拉伸建模得到液冷板幾何模型，液冷板結構尺寸如圖3所示(單位：mm)。

圖3 液冷板結構尺寸示意圖Fig.3 Schematic diagram of structural dimensions of liquid-cooled plate

為評估拓撲流道液冷板的散熱性能，在COMSOL軟件平臺上進行有限元仿真，采用自由四面體網格進行劃分。在仿真時做出假設：(1)內部流體為不可壓縮層流；(2)流固交界面無滑移邊界。數值模擬時滿足如下控制方程：

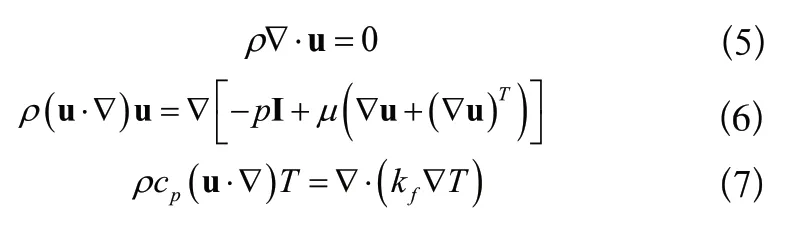
其中，式(5)、式(6)分別為連續性方程和動量守恒方程，式(7)為流體域的能量守恒方程，式(8)為固體域的能量守恒方程。

仿真時，冷卻套的固體材料為6061鋁合金，取常溫20 ℃下的純水為冷卻介質；各冷卻套的入口為左上側，出口為右下側；在入水口處施加恒定的質量流量；在冷卻套內表面施加180 W恒定功率的生熱源；分別取入水口雷諾數為200—1，200進行分析，其中入水口雷諾數由式(9)定義：

式中，流體密度=1.0×10kg·m； v為入口的流體速度，單位為m/s；為入口的水力直徑，單位為m；流體黏度=1.008×10Pa·s。

4 流體拓撲優化中的體積分數研究 (Research on volume fraction in fluid topology optimization)

4.1 體積分數對液冷板散熱性能的影響分析

在液冷板設計中，如圖4(a)、圖4(b)所示，在拓撲優化時增大流體域體積分數，流道平均橫截面間距變寬，分支增多。流道的熱交換面積與散熱性能正相關，流固換熱總面積為傳熱流道的上下壁面積(圖4(c)灰色)與側壁面積(圖4(c)白色)之和。

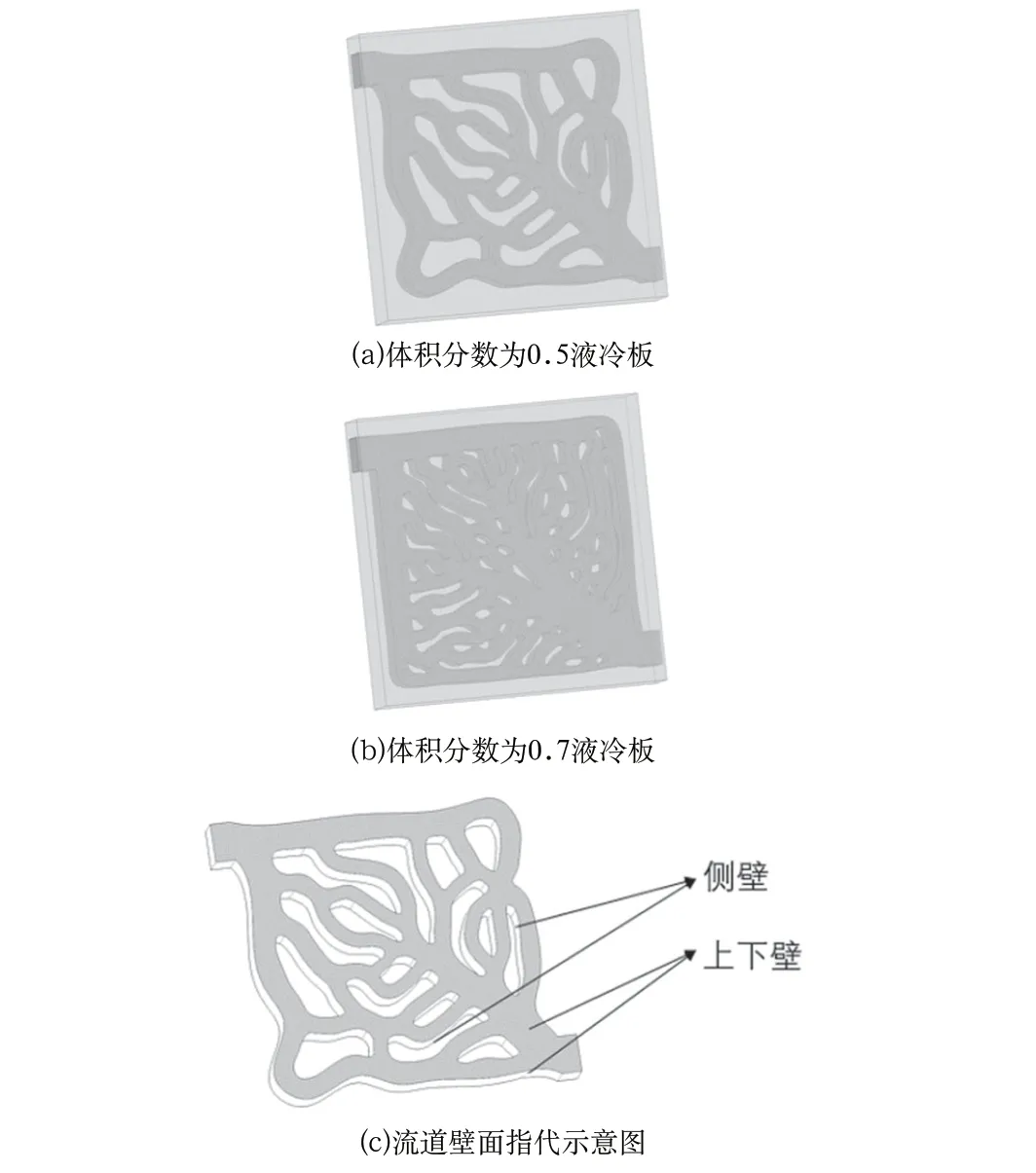
圖4 不同體積分數的拓撲流道形態示意圖Fig.4 Schematic diagram of topology passage patterns with different volume fraction

基于3.3.1的液冷板幾何模型，流固換熱總面積計算公式如下：

其中， L為拓撲優化得到的二維流道總邊界長度。當流體域體積分數增大到一定程度后，固體域也隨之變小，流道的總側壁面積變小，流固換熱總面積減小，液冷板的整體散熱能力也隨之變弱。所以，存在一個體積分數極值使拓撲優化得到的液冷板流固換熱總面積最大，液冷板的散熱性能最優。

為了找到該設計模型散熱性能最佳的流體域體積占比，首先以0.05為步長，取體積分數分別為0.5、0.55、0.6、0.65、0.7進行拓撲優化設計，優化數學模型為式(4)。以優化得到的結果為流道進行三維建模得到五個液冷板模型，使用3.3.2中的邊界條件進行仿真分析。

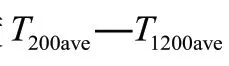
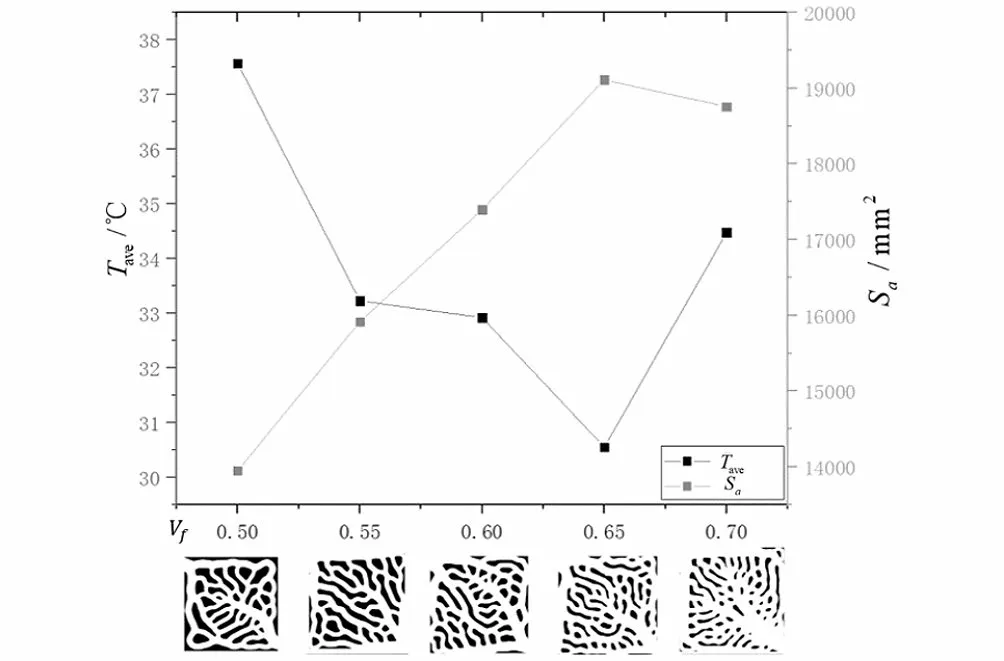
圖5 V f為[0.5,0.7]的液冷板流道形態及 Tave& S a折線圖Fig.5 Passage patterns of liquid-cooled plate if Vf is between 0.5 and 0.7，and their Tave& Sa line graph

基于上述分析，再以0.01為步長，取體積分數分別為0.61、0.62、0.63、0.64、0.66、0.67、0.68、0.69進行拓撲優化設計，優化數學模型為式(4)。以優化得到的結果為流道進行三維建模得到八個液冷板模型，使用3.3.2中的邊界條件進行仿真分析。加上=0.65和=0.7的兩個模型，對10個模型的仿真結果進行分析，繪制&折線圖，如圖6所示。由圖6可知，在為[0.61，0.7]區間，隨著的增大，流固換熱總面積先單調遞增再單調遞減，液冷板的受熱面平均溫度先單調遞減再單調遞增，在體積分數為0.65處的最大且最低，故體積分數最優值應在(0.64，0.66)區間，在拓撲優化時建議取=0.65。

圖6 V f為[0.61,0.7]的液冷板流道形態及 Tave& S a折線圖Fig.6 Passage patterns of liquid-cooled plate if Vf is between 0.61 and 0.7，and their Tave& Sa line graph

4.2 在不同設計域尺寸下體積分數對拓撲優化設計結果的影響

由于熱源工況形狀各異，在實際生產應用時可能需要針對不同尺寸的設計域進行拓撲優化設計。為檢驗流體域體積分數對不同尺寸設計域的拓撲優化設計結果影響情況是否一致，在3.1所述的設計域尺寸基礎上改變設計域尺寸，保持進出水口尺寸不變，將設計域邊長尺寸分別設置為橫∶縱=3L∶6L(圖7(a))、橫∶縱=6L∶3L(圖7(b))。再分別以0.05為步長，取體積分數分別為0.5、0.55、0.6、0.65、0.7進行拓撲優化設計，優化數學模型為式(4)。以優化得到的結果為流道進行三維建模得到五個液冷板模型，使用3.3.2中的邊界條件進行仿真分析。繪制&折線圖，如圖7所示，在 V為[0.5，0.7]區間，隨著的增大，流固換熱總面積先單調遞增再單調遞減，液冷板的受熱面平均溫度先單調遞減再單調遞增，在體積分數為0.65處的S最大且最低，故體積分數最優值應在0.65相鄰區間。

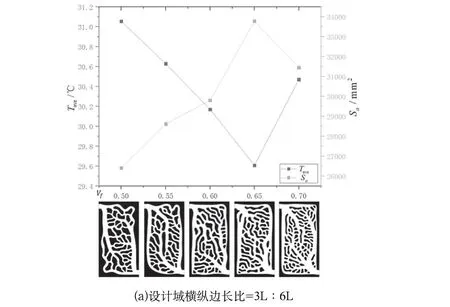
圖7 V f為[0.5,0.7]的長方形設計域液冷板流道形態及 Tave& Sa折線圖Fig.7 Passage patterns of liquid-cooled plate in rectangular design area if Vf is between 0.5 and 0.7，and their Tave& Sa line graph

4.3 非線性回歸分析

非線性回歸是回歸函數關于未知回歸系數具有非線性結構的回歸分析方法。將4.1中仿真得到的受熱面平均溫度均值通過IBM SPSS進行一元非線性回歸分析，得到關于的預測模型：

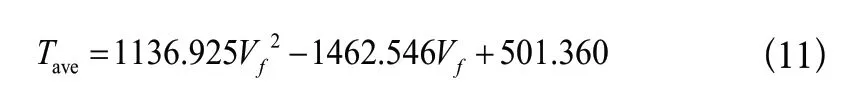
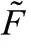
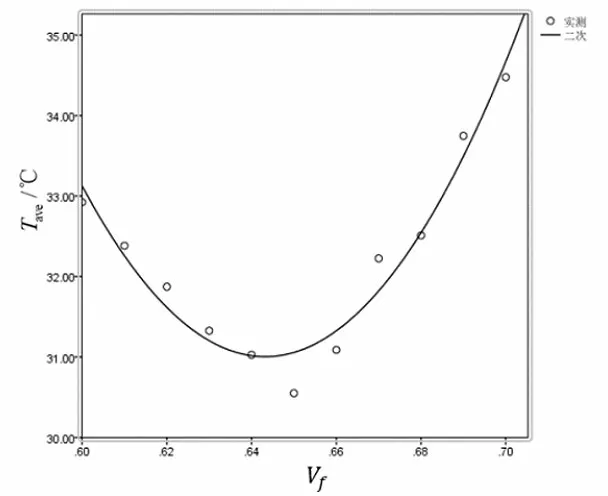
圖8 非線性回歸擬合曲線圖Fig.8 Diagram of nonlinear regression fitting curve

5 結論(Conclusion)

本文針對基于SIMP法的流體散熱液冷板拓撲優化設計中的體積分數取值問題進行了系統性的數值分析，使用控制變量法在以流固邊界換熱量最大為目標的優化數學模型中改變體積分數取值進行流道拓撲優化設計，并分別進行液冷板幾何建模及仿真分析，統計液冷板受熱面平均溫度數值及流固換熱總面積；而后改變設計域形狀尺寸檢驗體積分數取值規律的普適性；最后將仿真數據進行非線性回歸分析，得出體積分數對流道散熱性能的預測數學模型，計算得出流體散熱拓撲優化問題的體積分數最優值應在(0.64，0.65)區間的結論，為此類散熱流道拓撲優化設計提供了有價值的設計指導建議。