恒力車削過程的模糊指數趨近律互補滑模控制

陳高華 張嫣然 李 悅

(太原科技大學電子信息工程學院 山西 太原 030024)

0 引 言

近年來，機械制造追求更加便捷、快速、高效的加工方式[1]。傳統加工采用恒進給速度加工，為防止切削力過大損壞機床與刀具，只能選擇較低的進給速度，導致加工時間長，加工精度低，無法滿足新時代機械加工要求。而恒切削力加工，采用的是變進給速度加工，可以在切深較小時進行高速加工。恒力加工相較于傳統的加工方式縮短了加工時間，提高了加工精度，延長了機床壽命[2]。

恒力切削對于加工過程實現快速化、高效化有重要作用，因此成為眾多學者的研究對象。宋曉華[3]提出基于PID控制與模糊控制的切削加工過程雙模控制，當偏差大時用模糊控制，偏差小時轉由PID控制；張毅等[4]提出一種將預測控制與神經網絡相結合的神經網絡預測控制應用于恒力車削，使切削進給在切削深度發生突變前提前發生相應變化；余銘奇等[5]提出一種加工過程的模糊自適應PID的控制方法，運用模糊自適應PID控制方法，系統的調節時間縮短，響應速度加快，抗干擾能力和適應參數變化的能力要優于增益自適應的PID控制；陳首彥[6]提出采用模糊滑模控制應用與機器人切削，根據加工狀態利用模糊規則調整滑模控制系數，進而改變進給速度，實現對機器人切削的切削力控制；Xu等[7]提出將前饋神經網絡控制與自適應控制結合的控制方式，并且加工之前離線優化切削參數，該方法有好的穩定性和適用性；Zuperl等[8]提出將模糊控制與自適應控制相結合，實時修正模糊規則，實現在線調整進給速度，進而實現恒力切削；Liu等[9]建立了主軸電流與進給速度之間的數學模型，特別之處在于其檢測并提取了主軸電流，將主軸電流作為反饋，所使用的控制方法是模糊控制與自適應控制相結合的方式。上述方法在恒力切削控制的研究方面取得了一定成果，但是在切深突變時切削力均出現了較大的超調，而采用滑模控制(Sliding Mode Control，SMC)可以很好地削減這一超調。加工過程具有很強的時變性、非線性、不確定性[10]。滑模控制作為一種魯棒控制方法，對外部干擾和未建模動態具有完全的魯棒性，因此對控制加工過程有其獨特的優勢，但滑模控制器存在輸出抖振的缺陷，且無法消除，只能削弱。國內外眾多學者就削弱滑模控制器輸出抖振進行了大量研究[11-21]，其中包括采用改進現有的趨近律、非線性滑模面、觀測器，以及與現有其他控制器結合或將幾種方法混合使用等各種研究。

本文采用積分滑模面與互補滑模面結合的方法設計了互補滑模變結構控制器(Complementary Sliding Mode Controller，CSMC)，并將其與模糊控制結合，設計了一種用模糊控制策略實時整定指數趨近律指數系數的互補滑模控制器(Fuzzy Complementary Sliding Mode Control，F-CSMC)應用于恒力車削控制，并分別在切削深度臺階型變化與斜坡變化兩種情況下進行了仿真研究。互補滑模控制中，采用積分滑模面與互補滑模面結合的方式，但其本質仍為線性滑模面，因此，兼具了積分滑模面與線性滑模面的優點，既削弱了抖振，提高了控制精度，又保持了滑模面降階特性。在模糊控制中，通過模糊控制策略實時整定指數趨近律指數系數，降低切換控制的影響，可以在保證系統魯棒性的同時削弱抖振。當運動點距離滑模面遠時，加快收斂速度縮短收斂時間；當運動點到達滑模面附近時，減小趨近速度，有效地削弱傳統滑模控制器的輸出抖振。僅通過整定指數趨近律的一個參數指數系數就可以既實現縮短系統的收斂時間又削弱抖振，相較于同時整定兩個參數節省了計算量。

1 車削過程建模

車削過程由伺服機構、機械傳動和車削過程三個環節構成[22]，車削過程系統控制框圖如圖1所示，其中：Fn為給定切削力；F為檢測切削力；e為誤差；u為伺服電壓；Vf為進給速度；f為進給量；Fs為實際切削力。

圖1 車削過程系統控制框圖

伺服機構可簡化為一個二階系統：

(1)

式中：Vf為進給速率；u為電樞電壓；Km為伺服增益；ωn為伺服系統的自然頻率；ξ為阻尼系數。

機械傳動裝置簡化為進給量與進給速度之間的關系：

(2)

式中：p為刀具齒數，車削時為1；n為電機轉速。

加工過程中進給量與切削力之間的關系可用切削力經驗公式表示：

(3)

式中：Ks為切削系數，α與β是指數系數，三個系數均由大量實驗后憑借經驗給出；ap為切削深度，為本文的主動變化量。

因此，車削過程的傳遞函數為：

(4)

式中：Kd為測力儀轉化系數。

2 互補滑模控制器設計

由式(4)可得到切削過程的微分方程：

(5)

取狀態變量：

(6)

確定傳統線性滑模面為：

(7)

式中：c為常數。

采用等效控制與切換控制共同作用的控制方式，其中等效控制保證滑動模態運動品質，切換控制保證系統運動點有限時間內到達滑模面，而利用指數趨近律既可以保證滑動模態到達階段的動態品質，也可以削弱抖振[23]。傳統線性滑模控制器輸出uSMC為：

cx2-εcx1-εx2-Ksgn(s)]

(8)

式中：K為切換增益。

針對線性滑模控制，定義Lyapunov函數為V=s2/2。

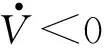
證明將指數趨近律公式代入Lyapunov函數中可得：

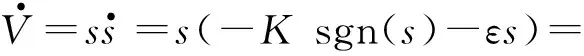
-K|s|-εs2=-(K|s|+εs2)

(9)

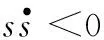
互補滑模控制器的滑模面采用積分滑模面與互補滑模面結合的方式。其中，積分滑模面定義為：

(10)

Bu+2λx2+λ2x1

(11)

定義廣義滑模面為：

(12)

由于積分滑模面與廣義滑模面存在同一參數λ，因此，可以得到它們的和為：

(13)

且積分滑模面與互補滑模面存在以下關系：

(14)

對互補滑模控制，定義Lyapunov函數為：

(15)

對Lyapunov函數求導并結合式(14)可得：

(16)

根據式(16)得到互補滑模控制器的輸出：

(17)

ucsw=-Ksgn(Sg+Sc)-ε(Sg+Sc)

(18)

uCSMC=uceq+ucsw

(19)

并將式(17)-式(19)代入式(16)可得：

(Sg+Sc)[-Bucw-λ(Sg+Sc)]=

-λ(Sg+Sc)2-(Sg+Sc)·ρsgn(Sg+Sc)≤

-λ(Sg+Sc)2-|Sg+Sc|·ρ≤0

(20)

所構造的Lyapunov函數滿足定理1，因此，所設計的互補滑模控制器可以使系統狀態運動在有限時間內到達滑模面且系統穩定。互補滑模控制下，狀態軌跡由滑模面外到達積分滑模面與互補滑模面的交線處，最終沿著交線到達原點。

3 趨近律參數ε整定

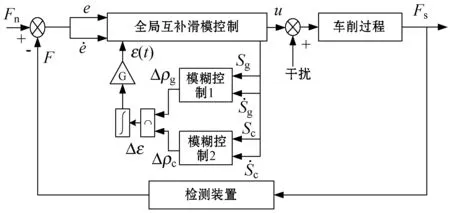
圖2 模糊滑模控制器結構框圖

模糊控制1與模糊控制2高度相似，其設計方法、隸屬度函數及模糊規則也是相同的。定義模糊控制器的輸入/輸出模糊集均為{NB,NM,NS,Z,PS,PM,PB}，分別表示負大、負中、負小、零、正小、正中、正大。模糊控制的輸入采用三角形隸屬度函數，邊界用S型隸屬度函數，輸入隸屬度函數如圖3所示；模糊控制的輸出采用鐘形隸屬度函數，輸出隸屬度函數如圖4所示。

(a) 輸入Sg/Sc隸屬度函數

(b) 輸入隸屬度函數圖3 輸入隸屬度函數

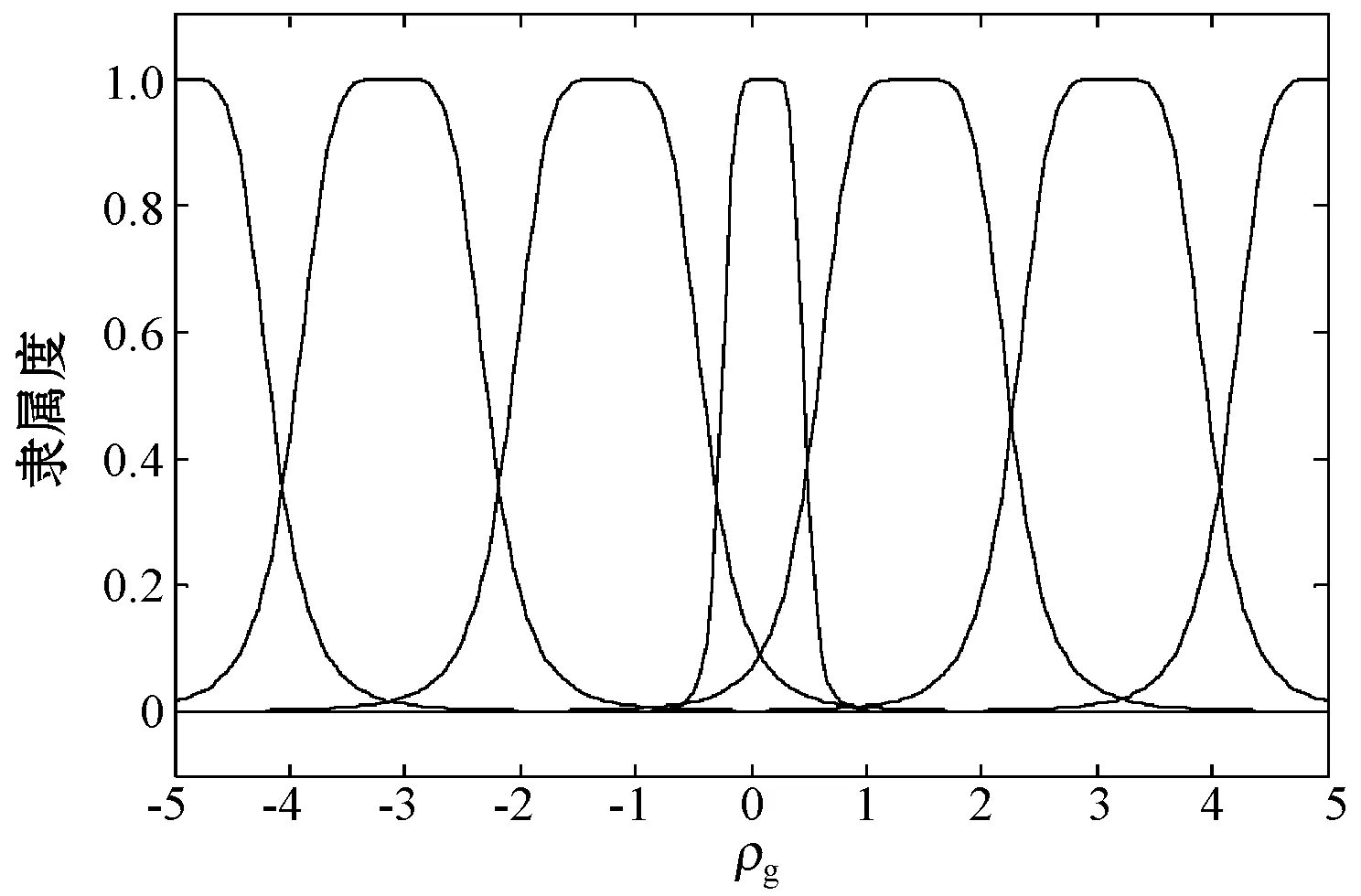
圖4 輸出Δρg、Δρc、Δε隸屬度函數

所設計的模糊規則如表1所示。

表1 模糊規則表

去模糊化采用重心法。對模糊控制1與模糊控制2的輸出作“與”運算，得到模糊控制的最終輸出：

Δρ=Δρg∩Δρc=min(Δρg,Δρc)

(21)

由模糊控制得到輸出Δε，采用積分的方法對ε(t)的上界進行估計：

(22)

式中：G為不小于1的常數。

4 仿真與結果分析

設給定切削力為600 N，取車削過程模型的各項參數如表2所示。

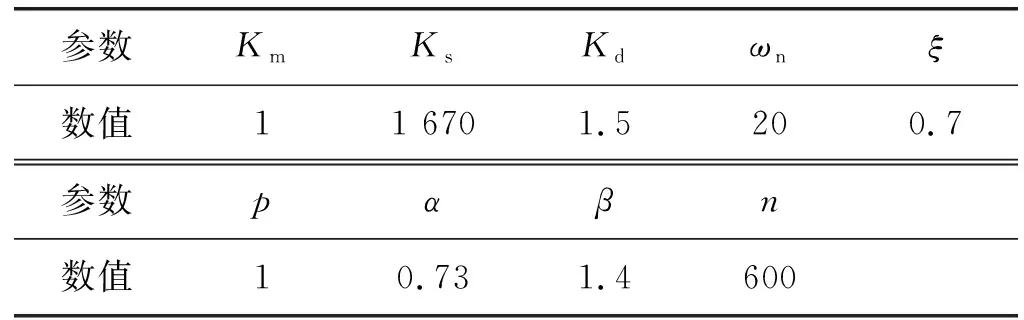
表2 車削過程模型的各項參數

將表1中的參數數值代入式(4)，得到車削加工過程的模型為：

(23)

為了驗證本文方法的有效性，按照式(23)在MATLAB/Simulink中搭建車削過程模型，并分別在本文方法與指數趨近律參數固定的互補滑模控制方法、傳統線性滑模控制方法及文獻[26]采用的PID/PD復合控制進行比較。并在t=5 s時加入一個值為50的脈沖干擾，觀察三種控制方法的抗干擾能力。

取指數趨近律參數固定的互補滑模控制器與傳統線性滑模控制器的參數為c=25、λ=12.5、K=60、ε=5。本文方法模糊指數趨近律互補滑模控制器的參數為c=25、λ=12.5、K=60，ε由模糊控制方法在線整定。互補滑模控制與傳統線性滑模控制按照式(8)與式(19)在Simulink中搭建仿真，模糊控制利用MATLAB中M文件嵌套進Simulink中進行參數整定。切深線性變化的情況下，在文獻[26]采用的PID/PD復合控制方法下的切削力響應曲線如圖5所示。傳統線性滑模控制、互補滑模控制及模糊互補滑模控制下的切削力響應曲線如圖6所示。

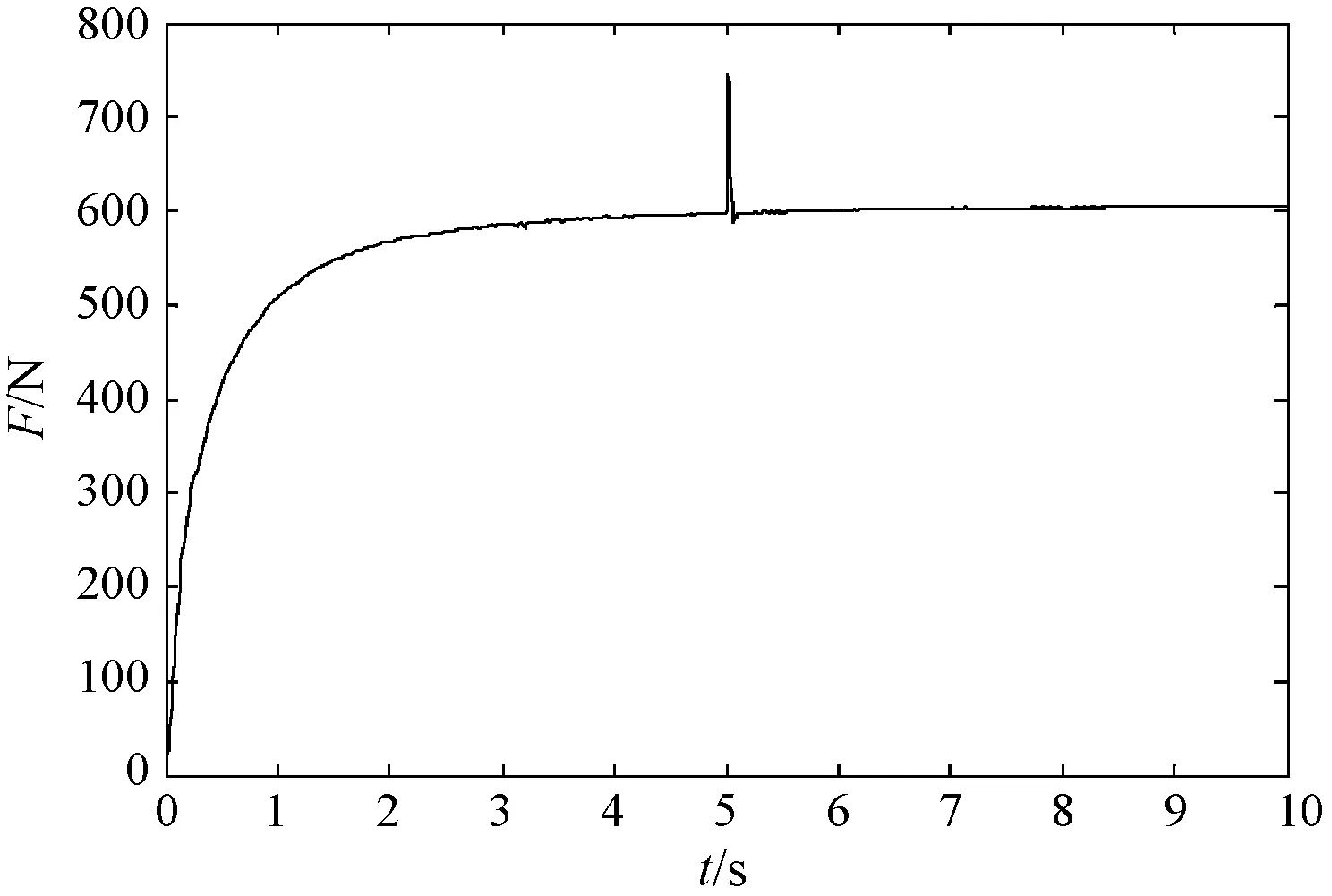
圖5 切深線性變化時文獻方法的切削力響應曲線

可以看出，當切深線性變化時，相較于文獻[26]所用PID/PD復合控制方法，滑模控制方法的調節時間明顯減小，抗干擾能力明顯增強。由圖6可看出本文方法的抗干擾能力、抖振大小、上升時間等指標均優于互補滑模控制方法和傳統線性滑模控制方法。本文方法控制下的切削力響應曲線上升時間最短，抖振最小，抗干擾能力最強。

在切深每一秒發生一次突變的情況下，PID/PD復合控制方法下的切削力響應曲線如圖7所示，傳統線性滑模控制、互補滑模控制及模糊互補滑模控制下的切削力響應曲線如圖8所示。

圖6 切深線性變化時SMC、CSMC及F-CSMC下的切削力響應曲線

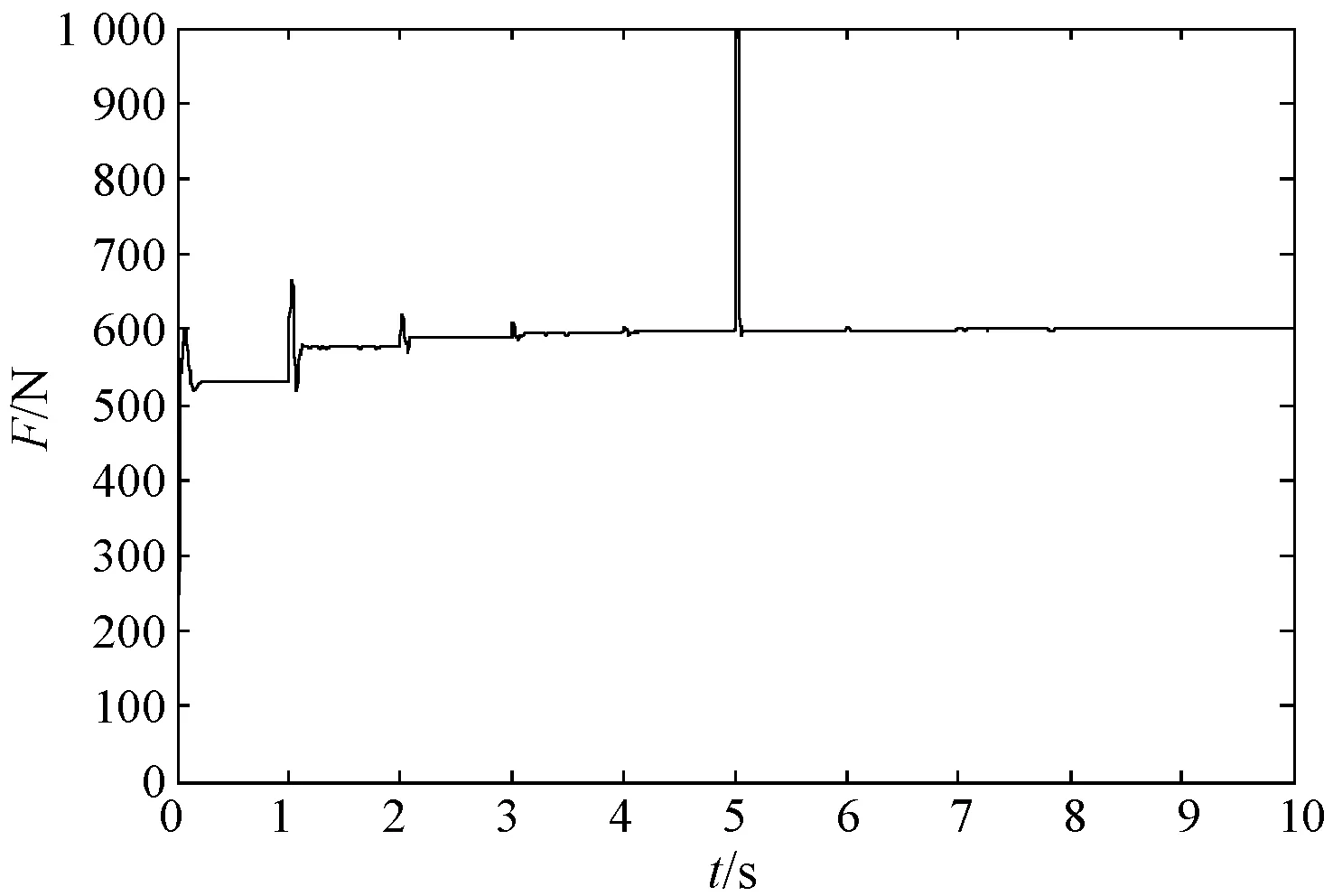
圖7 切深突變時文獻方法的切削力響應曲線

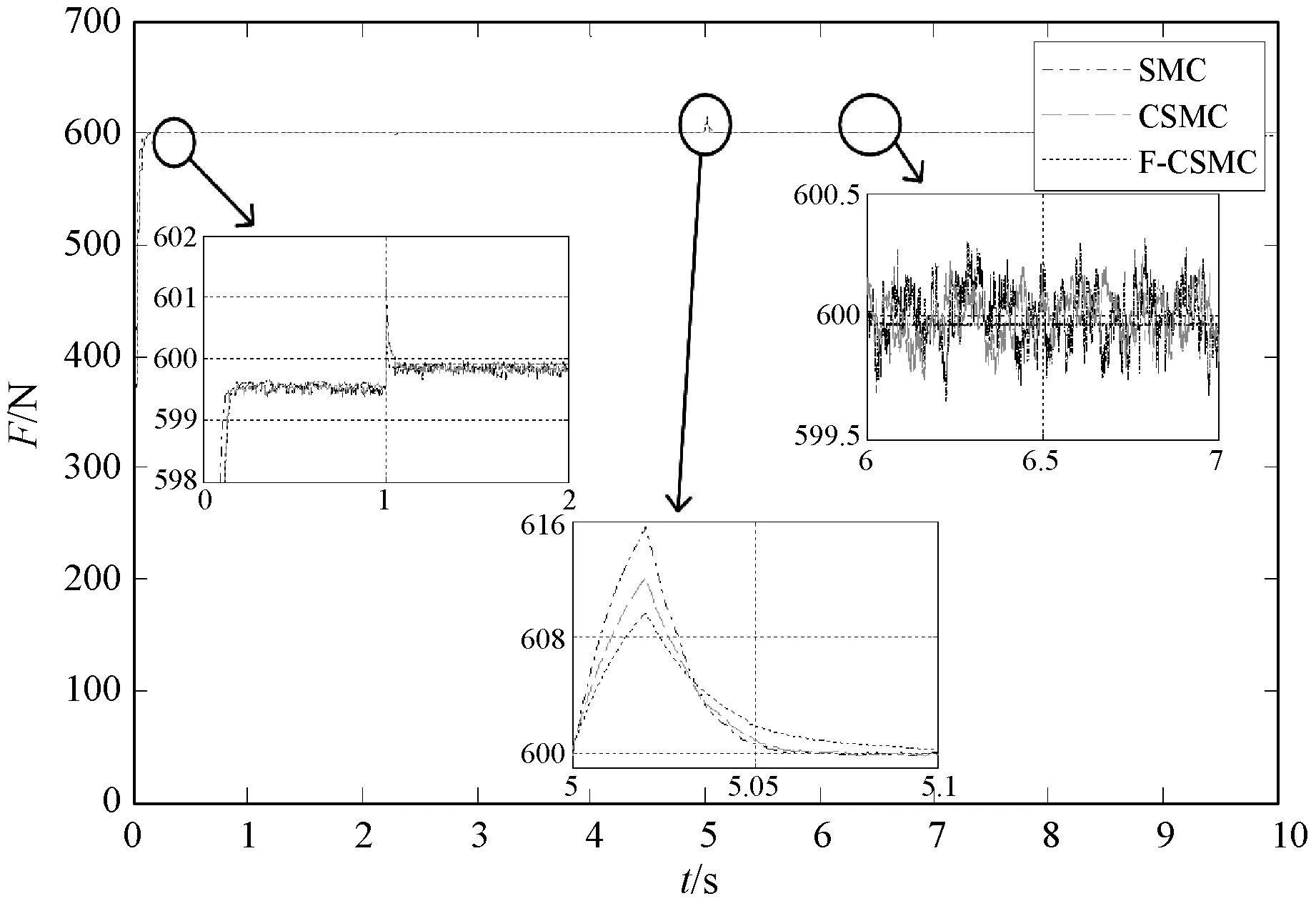
圖8 切深突變時SMC、CSMC及F-CSMC下的切削力響應曲線

切深突變情況下，本文所提的車削過程的模糊指數趨近律互補滑模控制、趨近律參數ε恒定不變的指數趨近律互補滑模控制、傳統線性滑模控制及PID/PD復合控制四種種控制方式的性能指標比較如表3所示。

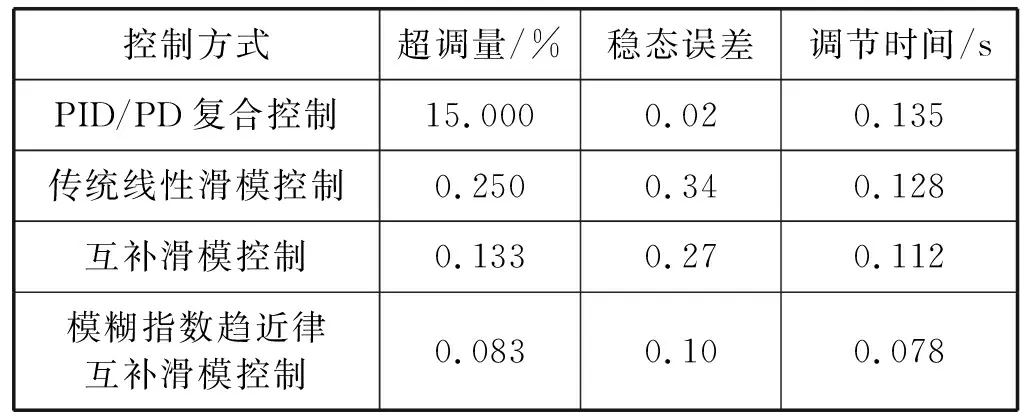
表3 四種控制方式下性能指標比較

可以看出，當切深突變時，文獻[26]所采用的PID/PD復合控制方法超調大，對參數變化及擾動敏感。傳統線性滑模控制方法與文獻相比各性能指標有明顯改善；互補滑模控制下切削力響應曲線的各項性能指標又進一步改善；本文方法與互補滑模控制方法相比，其超調更小，抗干擾能力更強，收斂速度更快且抖振幅度有所減少。

5 結 語

本文針對車削過程的恒切削力控制問題，以切深變化時仍能保證切削力恒定為目標，考慮到車削過程的非線性、時變性及不確定性，提出車削過程的模糊指數趨近律互補滑模控制方法。并分別在切深突變和線性變化兩種情況下進行了仿真研究，結果表明，本文方法響應快、超調小，不僅一定程度上削弱了傳統線性滑模控制器的輸出抖振，而且增強了系統的魯棒性，提高了控制精度。本文對于優化切削工藝，使切削過程更加高效、快速有重要意義。