軸向循環載荷下加筋板極限承載性能分析

崔虎威，丁啟印

重慶交通大學 航運與船舶工程學院，重慶 400074

0 引 言

船體梁的總縱強度是船體結構安全最重要的保障，隨著極限強度理念在船舶結構設計領域的逐步應用，船體結構設計不僅需要確定結構的尺寸，而且還需要準確評估其極限強度。長期以來，船體結構極限強度評估主要是基于一次性破壞的靜力極限強度評估理念。最早進行船體梁極限強度評估的是Caldwell，其于1965 年發表了一篇關于船體梁極限強度計算的論文[1]，標志著船體梁靜力極限強度評估理念進入客觀研究的實質性階段。目前，基于該理念開展的研究工作已非常成熟，并已進入實用階段。自2006 年4 月起，對油船、散貨船進行的極限強度評估已由國際船級社協會納入共同結構規范[2-3]的強制性要求中，隨后，國際標準組織[4]、國際海事協會[5-6]等又相繼納入了船體梁極限強度評估條款。以上評估條款均是以一次性破壞的靜力極限強度評估理念為基礎。

客觀上講，伴隨著波浪載荷的循環往復，船體梁所受到的總縱彎矩及其變形也是循環往復的。由于靜力極限強度準則不能考慮循環載荷的影響，部分學者認為基于循環載荷視角的船體結構累積塑性破壞或安定性破壞極限強度理念更符合船體結構極限強度失效機理。文獻[7]和文獻[8]相繼提出要重視循環載荷下船體結構因累積塑性而導致破壞的問題。人們總是從災難和對失敗的反思中得到啟發，例如日本一艘大型運輸船“尾道丸”號因遭遇惡劣的風浪及砰擊致使該船的船體在危險剖面處折斷，基于此，日本眾多知名學者又重新提出了船體結構累積塑性破壞問題[9]。國內學者黃震球等[10-12]最早提出了開展循環載荷下船體結構累積塑性破壞研究的重要性，認為累積塑性破壞準則是靜力極限強度準則的一個發展方向，應該成為今后船舶總強度研究的一個重要方面。近年來，有關循環載荷下船體結構的累積塑性破壞極限強度研究已初見成效。Cui 等[13-17]就循環載荷下船體結構的塑性累積破壞極限強度問題開展了研究。循環載荷下船體梁的安定性破壞極限強度問題，和Caldwell[1]的靜力極限強度問題是同一時期被提出的。首先將循環載荷下的船體結構彈性安定狀態引入船體梁極限強度研究的是Jones[18]，其研究表明，當考慮循環載荷下船體結構的彈性安定效應時，船體梁的垂向彎矩承載能力總是小于或是不超過船體梁的靜力一次性極限強度值，進而Jones 認為，相比Caldwell[1]的船體梁一次性靜力極限強度評估理念，安定性破壞極限強度評估理念更應該成為船體梁極限強度評估的基礎。Gannon 等[19]采用非線性有限元研究了安定效應對T 型船體加筋板焊接殘余應力的影響，發現因安定效應而導致極限強度增加的潛力取決于加筋板自身的失效模式。Zhang 等[20]將循環彎矩下船體梁的安定破壞作為評估和保障船舶總縱強度的重要方面，采用增量有限元方法計算了循環彎矩下船體梁的彈性臨界安定彎矩值。

以上有關船體結構累積塑性和安定性破壞極限強度理念的研究非常有益于船體結構的極限強度高精度評估，但卻不夠充分和深入，還有待于后續工作的持續開展。目前，在所有船體梁極限強度評估方法中，最具代表性的是非線性有限元法和逐步崩潰Smith 法[21]，針對這2 種評估方法的系統的介紹可參見文獻[22]。在基于非線性有限元方法的船體結構靜力極限強度評估中，出于將船體結構材料的強化潛力作為極限強度評估結果的安全裕度的考慮，船體結構的材料本構關系普遍采用理想彈塑性模型，即忽略材料的塑性強化影響。而Smith 法的基本特點則是將船體梁橫剖面劃分為一系列由帶板-加強筋組成的結構單元。在該方法中，每個單元的平均應力-應變關系在船體梁逐步崩潰極限強度計算前需預先給定，其核心是尋求合適的結構單元平均應力-應變關系。船體加筋板作為船體梁的基本構件，其在軸向載荷下的極限承載性能決定了船體梁整體的極限彎矩強度。本文區別于傳統的靜力極限強度評估理念，將著眼于循環載荷下船體加筋板的承載性能問題，以Smith 法所依賴的加筋板格單元的平均應力-應變關系為分析對象，針對一塊加筋板討論在不同評估理念或載荷模式下，船體加筋板的非線性有限元分析材料模型選擇對其極限強度、塑性變形分布等極限承載性能的影響。

1 有限元模型

1.1 模型尺寸與邊界條件

采用單彎-雙跨模型并考慮強橫梁構件的影響，其中強橫梁構件不實際建出，通過自由度約束來代替，單跨長度1 000 mm。邊界條件采用文獻[23]中對加筋板所取的邊界條件，即一端約束加載方向的位移，另一端加載，加載端的橫截面節點耦合加載方向的位移。在循環載荷有限元數值模擬中，采用位移控制對主節點施加強迫位移，提取的主節點支反力及位移可換算成加筋板的平均應力-應變曲線。加筋板的幾何尺寸及邊界條件分別如表1 和表2 所示。表2 中，U表示位移，R表示轉動，x指板長度方向，y指板寬度方向，z指加強筋高度方向。采用ANSYS 中的Shell 181 單元對結構進行離散，非線性有限元模型與加筋板結構的幾何圖如圖1 所示。表3 給出了單次壓縮下不同網格尺寸加筋板非線性有限元極限強度計算結果，為保證計算精度并兼顧計算效率，本文采用 25 mm×25 mm的單元尺寸。

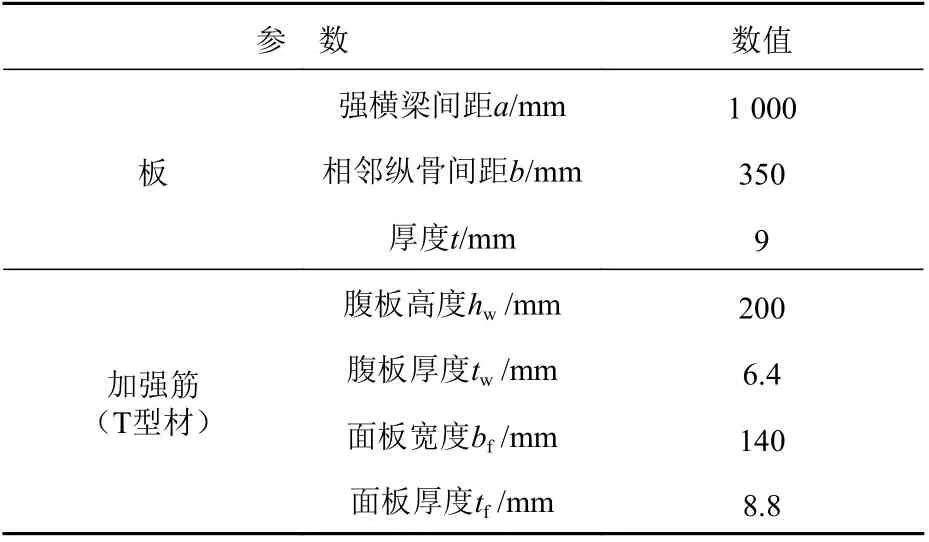
表1 加筋板單元模型尺寸Table 1 Model size of stiffened plates

表2 加筋板單元邊界條件Table 2 Boundary conditions of stiffened plates

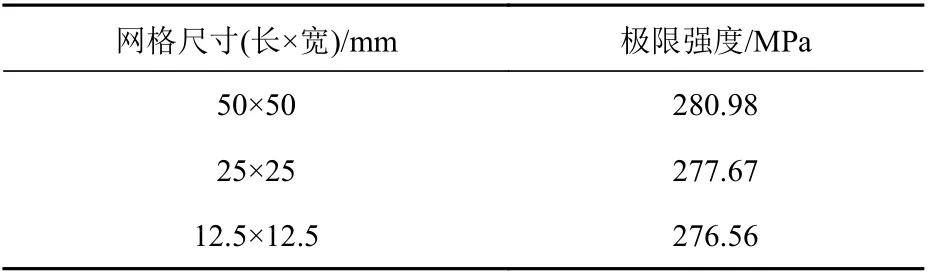
表3 不同網格尺寸加筋板單元極限強度數值計算結果Table 3 Numerical calculation results of ultimate strength of stiffened plates with different grid sizes

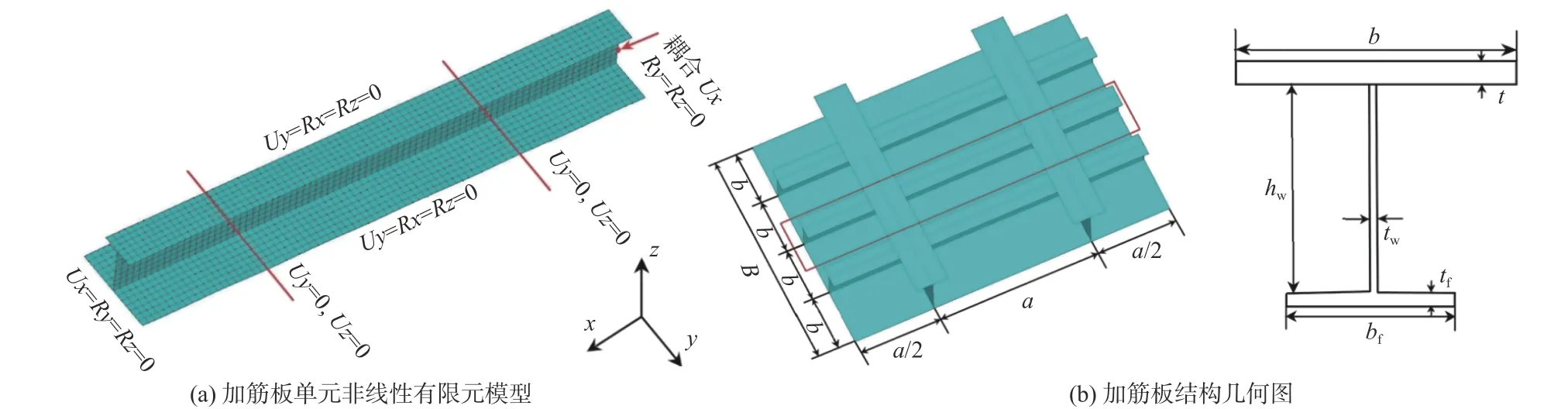
圖1 加筋板單元及加筋板結構示意圖Fig. 1 Schematic diagram of stiffened plate unit and stiffened plate structure

1.2 初始缺陷

由于焊接過程中的冷熱不均，船體結構在制造完工后有可能存在初始缺陷，這主要由兩方面構成：一是船體結構件在焊接加工制造中產生的焊接殘余應力；二是焊接初始撓度。考慮到循環載荷下焊接殘余應力可以在一定程度上得到釋放，故本文忽略焊接殘余應力，只考慮初始撓度。本文加筋板的初始撓度由以下3 個部分組成。

1） 板的初始撓度Wopl：

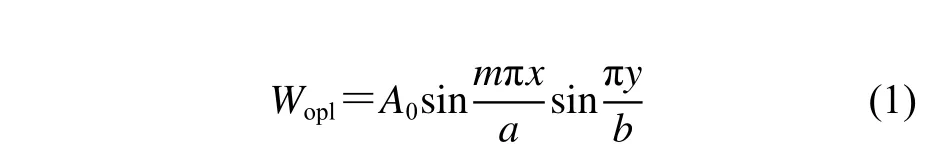
2） 加強筋的梁柱形初始撓度Woc：

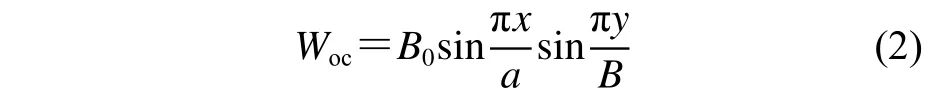
3） 加強筋的側傾初始撓度Wos：

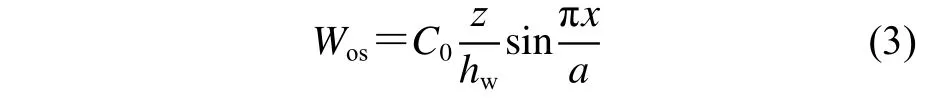
式中：B為加筋板寬度；A0，B0，C0為3 種初始變形的幅值；m為x方向初始撓度的半波數。取平均級別的初始撓度幅值，A0＝0.1β2t，B0＝C0＝0.001 5a，其中β為柔度系數，β＝(b/t)，σY為屈服強度，E為彈性模量。本文在ANSYS 中以APDL 方式將初始撓度施加到非線性有限元模型中。

2 材料本構關系與載荷工況

鋼質材料的本構關系，也即材料屬性對非線性有限元數值模擬具有重要影響，尤其是因塑性變形而導致的材料強化需要細致考慮。在現行的傳統一次性破壞靜力極限強度理念下，普遍采用理想彈塑性本構關系來對船體結構極限強度進行評估，所獲得的結果因忽略了材料的塑性強化影響而偏于保守，因此可將材料的塑性強化特性作為結構安全的裕度。另外，若將結構置于有較大塑性變形出現的循環載荷視角下，那么就需首先確定循環載荷下材料的塑性強化。本文針對不同的載荷工況，將分別選用理想彈塑性、各向同性強化及考慮反向加載鮑辛格效應[24]的Chaboche材料本構關系。Chaboche 材料本構關系的相關參數參見文獻[25]，其彈性模量E= 205 800 MPa，泊松比v= 0.3，屈服強度 σY= 285 MPa，鋼材牌號為S275[25]。具體的載荷工況與材料本構關系如表4所示，表中， εY為 初始屈服應變，G為剪切模量。

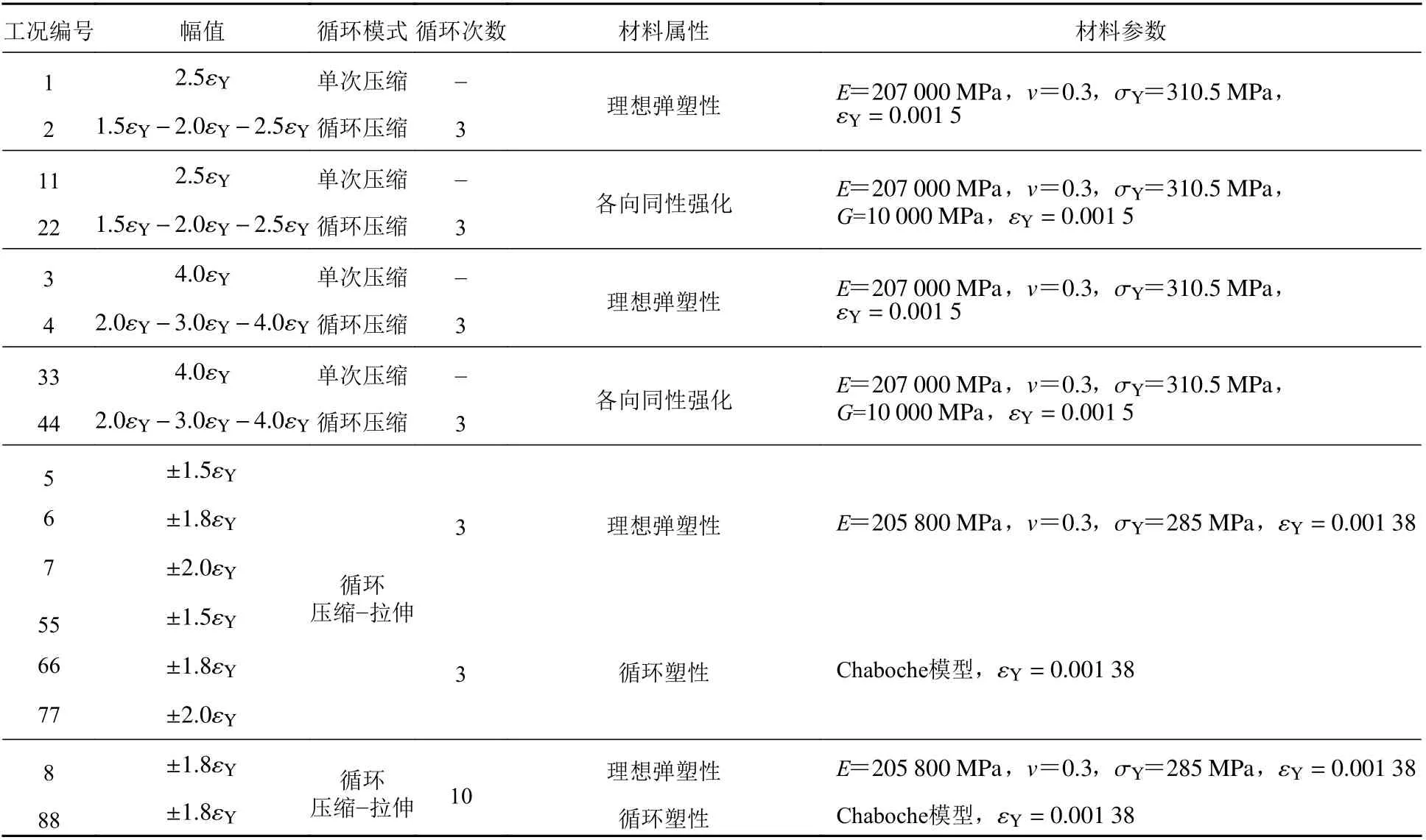
表4 載荷模式與材料屬性Table 4 Loading mode and material properties

3 計算結果

為了觀察各次循環壓縮極限狀態下加筋板的塑性屈服分布，本文給出了加筋板在各次循環下極限狀態時刻的von Mises 等效應力云圖。通常，可將平均應力-應變曲線用于反映整體結構的承載性能，其中平均應力可通過主節點支反力除以橫截面面積求取。在平均應力-應變曲線中，壓縮狀態下加筋板的平均應力最大值反映了其壓縮極限強度。循環載荷下加筋板的平均應力-應變曲線在下文中給出。

3.1 循環壓縮載荷下加筋板極限狀態von Mises 應力分布

圖2～圖4 示出了工況4 和工況44 下，在最大循環壓縮幅值 2.0εY下分別采用理想彈塑性及各向同性強化材料模型時各次極限狀態時刻的von Mises 應力分布，其中紅色區域代表塑性屈服區域。從中可以發現，隨著各次循環壓縮幅值的增加，在工況4 下，帶板的屈服區域由均勻分布轉變為向中部集中，塑性累積突出發生在帶板中部崩潰區域；而工況44 下的屈服區域則有擴大的趨勢，塑性累積在整體加筋板范圍內均有發生。各向同性強化材料模型對加筋板第1 次壓縮極限狀態下塑性屈服區域的影響較大，在后續循環中，其影響逐步降低。由圖4 可以發現，在工況4 和工況44 下，第3 次壓縮極限狀態時刻的屈服區域分布已較為一致。

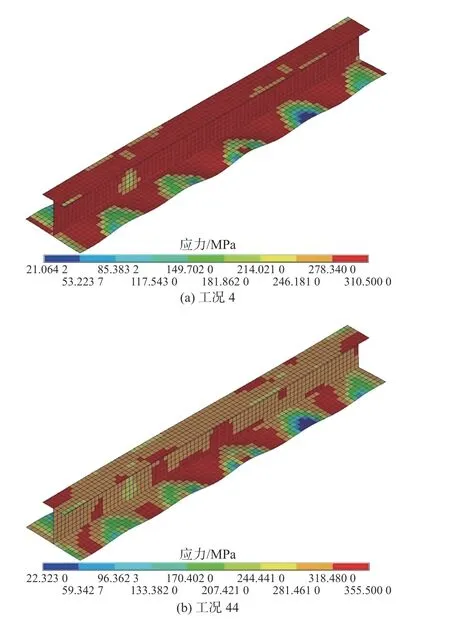
圖2 工況4 和工況44 下第1 次壓縮極限狀態Fig. 2 First compressive limit state of Case 4 and Case 44

圖3 工況4 和工況44 下第2 次壓縮極限狀態Fig. 3 Second compressive limit state of Case 4 and Case 44

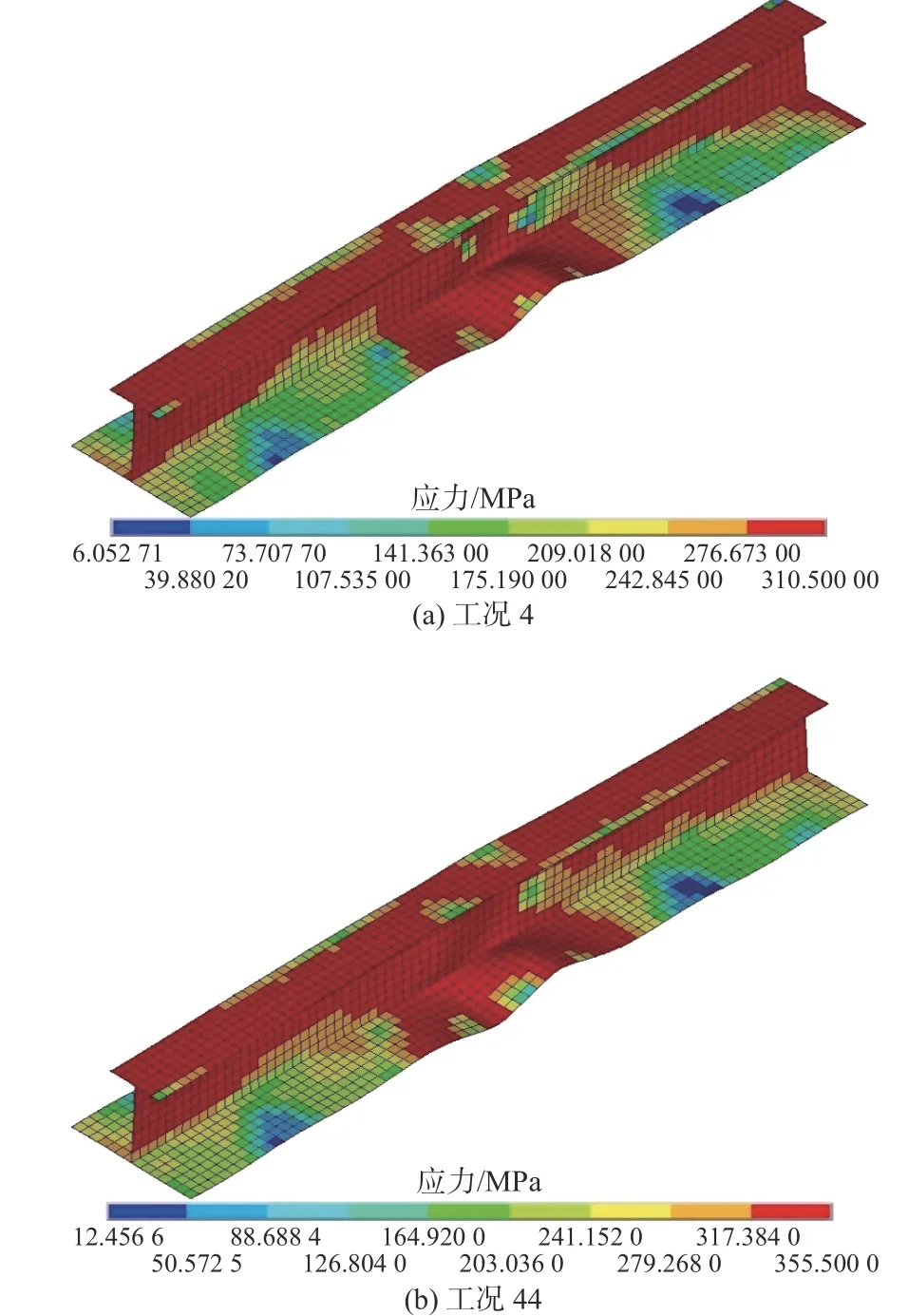
圖4 工況4 和工況44 下第3 次壓縮極限狀態Fig. 4 Third compressive limit state of Case 4 and Case 44

3.2 循環壓縮載荷下加筋板的平均應力-應變曲線

圖5 所示為采用理想彈塑性材料模型及各向同性材料模型時單調壓縮和循環壓縮的平均應力-應變曲線，圖中σ/σY為平均應力，ε/εY為平均應變。由圖中可發現，各向同性材料模型的各次壓縮極限強度均高于理想彈塑性材料模型，這2 種材料模型的各次壓縮極限強度是隨著應變的增加而減小的，且重新加載的路徑與前一次循環中的卸載路徑大致重合。理想彈塑性材料模型的單調壓縮曲線可近似作為循環加載曲線的包絡線，而各向同性材料模型的單調壓縮曲線則稍低于循環加載曲線的包絡線。

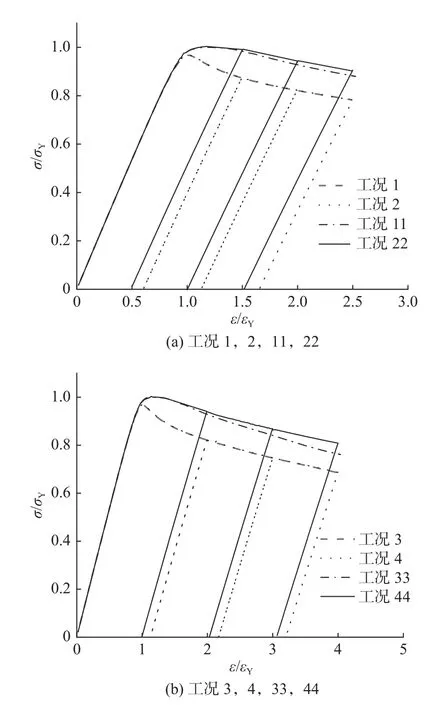
圖5 平均應力-應變曲線Fig. 5 Average stress-strain curves

3.3 循環壓縮-拉伸載荷下加筋板極限狀態von Mises 應力分布

圖6～圖8 示出了在工況6 和工況66 下，在相同循環載荷幅值下分別采用理想彈塑性及循環塑性Chaboche 材料模型時各次壓縮極限狀態時刻的von Mises 應力云圖，其中紅色區域代表塑性屈服區域。從中可以發現，在工況6 下，采用理想彈塑性材料模型時，在各次極限狀態時刻其塑性屈服區域在整個模型范圍內是廣泛分布的；而由于循環塑性材料模型的采用，在工況66 下，在各次極限狀態時刻其塑性屈服區域集中分布在局部區域，且隨著循環次數的增加塑性屈服區域呈明顯縮小的趨勢。這表明循環塑性材料屬性對循環載荷下加筋板的塑性屈服具有重要影響，在分析其極限強度特性時需要慎重考慮。

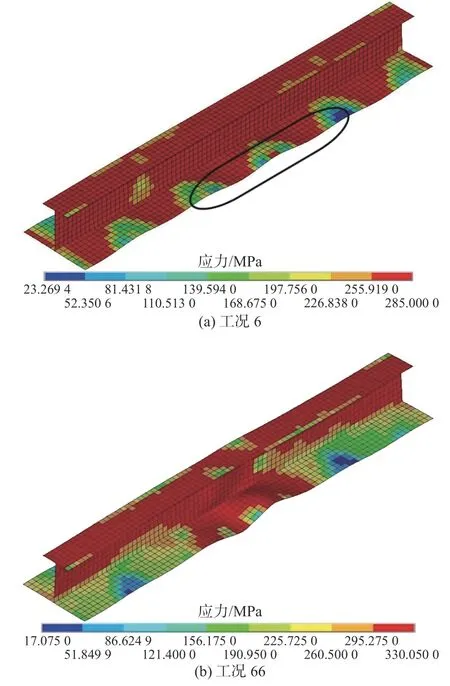
圖6 工況6 和工況66 下第1 次壓縮極限狀態Fig. 6 First compressive limit state of Case 6 and Case 66

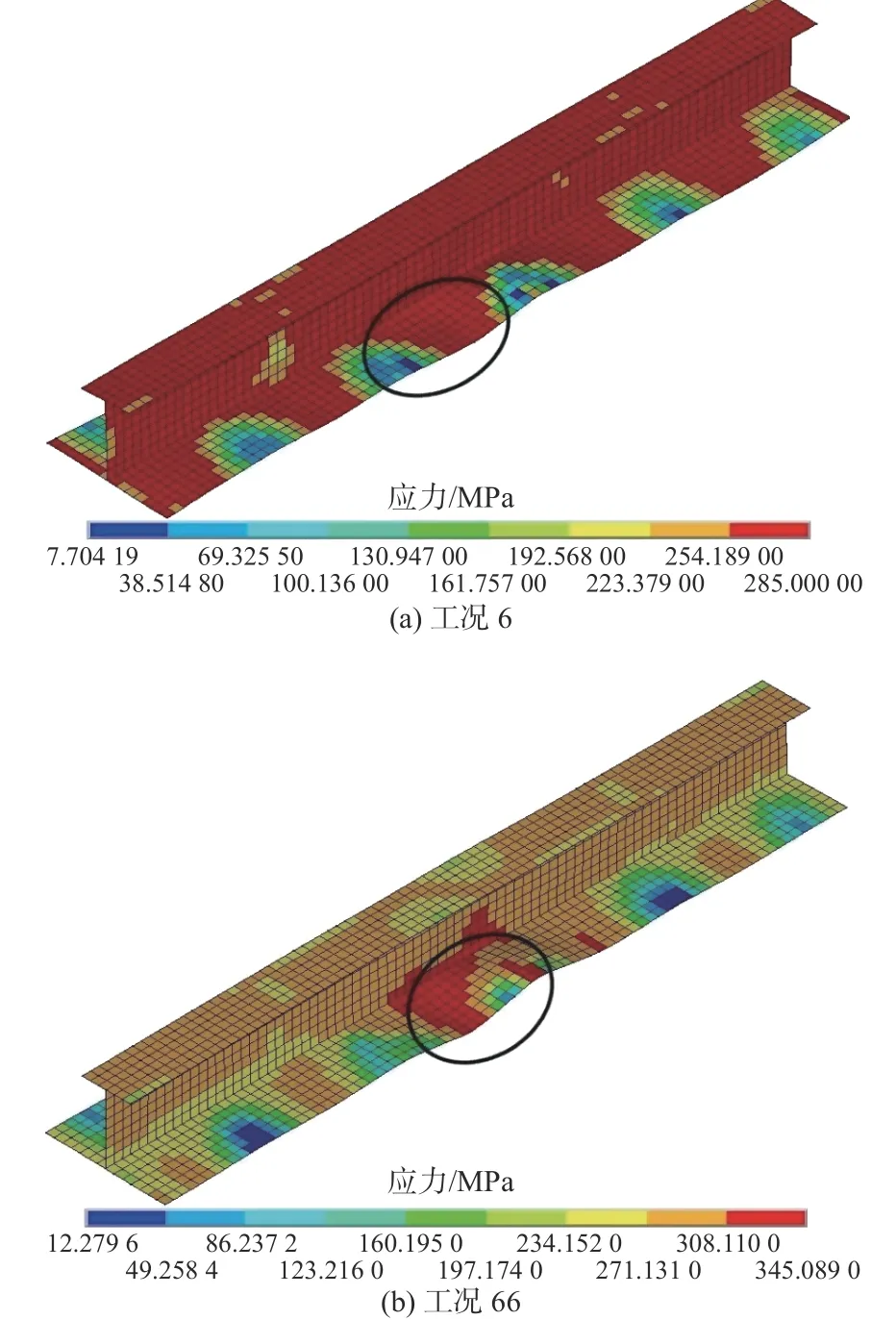
圖7 工況6 和工況66 下第2 次壓縮極限狀態Fig. 7 Second compressive limit state of Case 6 and Case 66

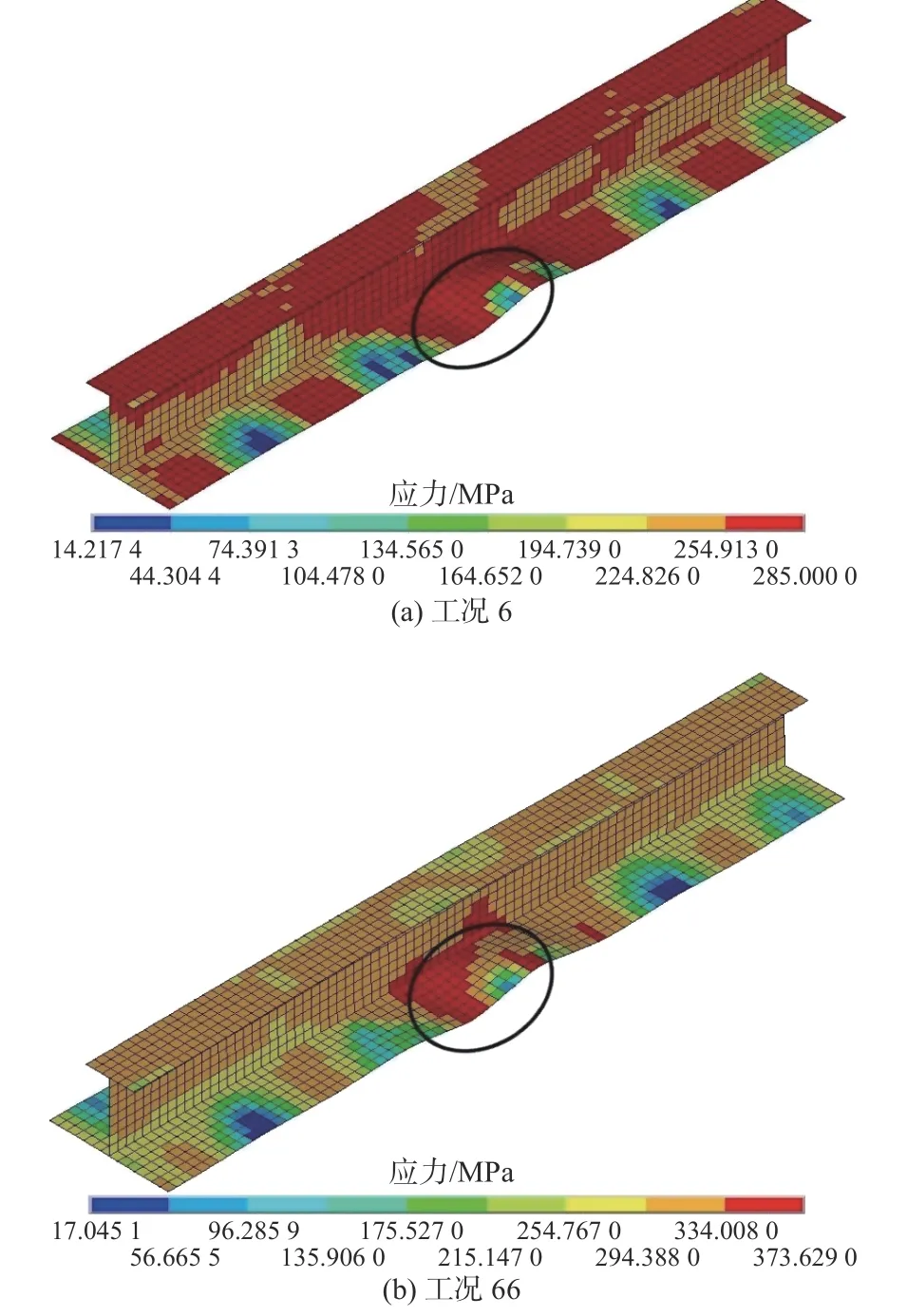
圖8 工況6 和工況66 下第3 次壓縮極限狀態Fig. 8 Third compressive limit state of Case 6 and Case 66

3.4 循環壓縮-拉伸載荷下加筋板的平均應力-應變曲線

圖9 所示為采用理想彈塑性及循環塑性Chaboche 材料模型的平均應力-應變曲線。從中可以看出，采用Chaboche 材料模型時其第1 次壓縮和拉伸極限強度均比采用理想彈塑性模型時大；在后續的循環中，采用理想彈塑性材料模型時的壓縮極限強度相比Chaboche 材料模型有明顯的下降。在抗拉強度上，Chaboche 材料模型在各次循環中其拉伸極限強度均稍大于理想彈塑性模型。總的來說，使用Chaboche 材料模型的加筋板在循環拉壓下呈現較為穩定的極限承載性能，其壓縮、拉伸極限強度的下降程度相比理想彈塑性模型有所緩和。圖10 所示的10 次循環平均應力-應變曲線也反映了相似的特性。

圖9 3 次循環載荷下加筋板的平均應力- 應變曲線Fig. 9 Average stress-strain curves of stiffened plate under three cycles loads

圖10 10 次循環載荷下加筋板的平均應力- 應變曲線Fig. 10 Average stress-strain curves of stiffened plate under ten cycles loads

4 結 論

本文針對同一尺寸加筋板開展了軸向循環載荷下理想彈塑性、各向同性強化及循環塑性Chaboche 材料模型的非線性有限元極限承載性能對比計算，通過分析各次循環極限狀態時刻下的von Mises 應力分布，探討了加筋板的塑性屈服分布區域，并根據平均應力- 應變曲線觀察了加筋板在不同材料模型下的極限承載性能，主要得到如下結論：

1） 不論是在循環壓縮載荷下還是循環壓縮-拉伸載荷下，理想彈塑性材料模型在壓縮極限狀態下的塑性屈服區域分布最廣。

2） 循環塑性的加入使得加筋板在各次壓縮極限狀態下的塑性屈服區域逐步集中于局部區域，且呈逐漸縮小的趨勢。

3） 各向同性材料模型的各次壓縮極限強度均高于理想彈塑性材料模型，這2 種材料模型的各次壓縮極限強度是隨著應變的增加而減小的。

4） 循環塑性材料模型的引入使得加筋板在循環載荷下呈現出較理想彈塑性材料模型更為穩定的極限承載性能。