基于改進密度峰值聚類算法的軌跡行為分析

呂 奕，劉漫丹

華東理工大學 化工過程先進控制和優化技術教育部重點實驗室，上海 200030

教育管理信息化是信息化社會的重要組成部分。隨著校園信息化程度的不斷提高，利用校園網通過無線網絡的方式進行校園電子化信息管理成為主流，由此積累了大量的校園無線網絡數據。如何有效地分析和利用這些海量數據，從而讓其更好地服務于校園和教育，近年來成為一個熱點問題。根據用戶登錄無線網的位置及時間，并按照時間順序將位置依次連接起來，可以得到用戶軌跡信息。根據軌跡信息之間的相似性對群體特征進行深入探索和分析，可以有效推進校園網的更新迭代以及指導學生的網絡使用行為。

軌跡數據聚類[1]是軌跡分析的重要方面，其是將具有不同時間和空間相似度特征的時空對象劃分為多個類或簇，使同一類內的對象相似性程度高，而不同類之間數據的相似性程度低。針對軌跡行為分析已有不少研究成果。吳笛等人[2]對南海旋渦軌跡進行時空聚類分析，在空間聚類的基礎上提出軌跡線段時間距離的度量方法和閾值確定原則，驗證了基于密度的軌跡時空聚類方法的有效性。穆桃等人[3]通過分析多層網絡流量，利用多種機器學習方法，預測出用戶的地理位置類型和興趣愛好，并將兩者相結合提高用戶分類的準確性。李旭等人[4]通過構造用戶興趣度矩陣的方式改進用戶間相似度的計算方法，提出了基于興趣矩陣的相似度聚類算法。

對校園無線網絡軌跡行為特征進行聚類分析，一方面，可以根據不同集合中學生的軌跡特點將高校學生分為不同簇，分析判斷不同簇學生的特點，為高校教育教學方案提供依據，為學生管理系統提供決策支持[5]。另一方面，將離群點檢測算法與聚類算法相結合，可以因此判斷出學生中的離群學生并進行針對性處理。由于校園軌跡具有較強的規律性[6]，通過檢測學生的異常軌跡，可分析學生是否按時上課或者是否在教學期間內離校等問題，針對頻繁發生軌跡異常的學生進行有效的管理，密切關注使用者動態，防止意外事件發生[7]。

本文采用基于共享最近鄰的快速搜索密度峰值聚類算法（shared-nearest-neighbor-based clustering by fast search and find of density peaks，SNN-DPC）[8]對校園無線網絡軌跡進行聚類分析，在傳統的局部密度的核密度計算方式的基礎上，改進局部密度度量，使得算法適用于多比例、各密度以及數據集之間交叉纏繞等高維度的復雜數據集，更有利于對校園無線網絡數據進行聚類分析。聚類算法對離群點信息較為敏感，若將離群點算法與聚類算法相結合，可以有效減小離群點對整體聚類的影響。因此，本文將離群點檢測算法與SNN-DPC 聚類算法相結合，得到兩種改進后的SNN-DPC算法，兩種改進算法均克服了原有聚類算法對離群點敏感問題的不足。將算法應用于實際校園無線網絡信息處理中，可以定位瀏覽信息異常學生，為高校信息化建設提供了信息支持。

1 SNN-DPC算法介紹

SNN-DPC 算法是在基于密度峰值的快速搜索聚類算法（clustering by fast search and find of density peaks，CFSFDP）[9]的基礎上，考慮了每個點的鄰居的影響，引入了一種間接距離和密度的測量方法，利用共享鄰居的概念來描述點的局部密度和它們之間的距離[9]。

定義1（共享最近鄰數SNN）對于數據集X中的任意兩個點xi和xj，點xi的K個最近鄰集合（Γ(xi)）與點xj的K個最近鄰集合（Γ(xj)）的交集定義為共享最近鄰數SNN(xi,xj)。通常來說，兩個點共享的鄰居數目越多，則這兩個點越相似。共享最近鄰數用式（1）表示：

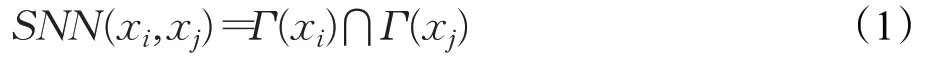
定義2（SNN相似度Sim(xi,xj)）點xi和xj之間的相似性程度稱為SNN相似度。對于數據集X中的點xi和xj，相似度可以定義為式（2）：

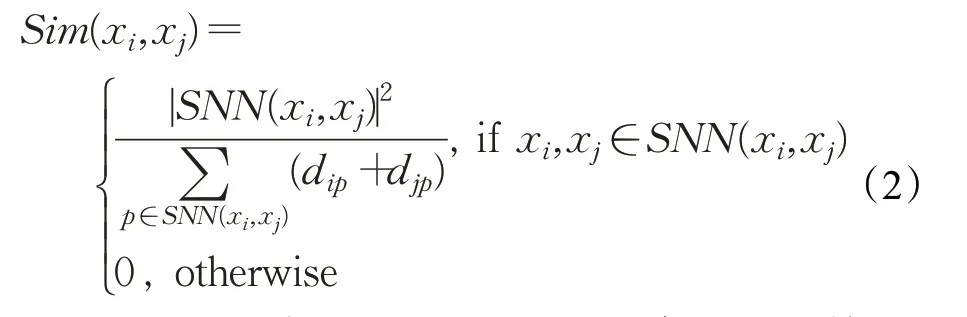
其中，SNN(xi,xj)表示點xi和xj的共享最近鄰數，d表示數據點間距離，通常為歐氏距離，點p為點xi和點xj共享的鄰居點，也就是說，僅當點xi和點xj出現在彼此的K鄰居集合中時，才計算SNN相似度。否則，點xi和點xj之間的SNN相似度為0。在定義任意兩個點的SNN 相似度之后，使用該相似度來計算點xi的局部密度ρi。

定義3（局部密度ρi）與點xi相似度最高的K個點的SNN相似度（Sim(xi,xj)）之和，用式（3）表示：

其中，L(xi)=(xi,…,xK)表示與點xi相似度最高的K個點的集合。

局部密度ρ不僅利用距離信息，而且還通過共享最近鄰數SNN 獲得有關聚類結構的信息，充分揭示了點與點之間的內在關系。

定義4（最近距離δi）計算點xi與其高于自身密度的點的最近距離δi（簡稱xi的最近距離）需要找到局部密度大于點xi的點xj，然后將數據點xi和xj之間的歐氏距離乘以這兩點分別與它們的最近鄰距離之和，取最小值。具體定義如式（4）所示：

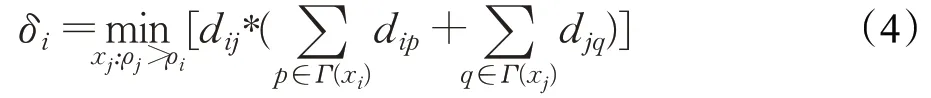
可以看出，最近距離δ不僅考慮了距離因素，同時考慮了每個點的鄰居信息，從而補償了低密度簇中的點，并提高了δ值的可行性，適應不同密度數據集。

密度最大點的δ值需要特殊定義，因為其是數據集X剩下所有點中δ最大的，如式（5）所示：

定義5（決策值γ）局部密度與最近距離之積。點xi的決策值γi用式（6）表示：

決策值γ的作用在于確定聚類中心點，通常來說，γ值越大，相應的ρ和δ越大，對應的數據點越有可能成為聚類中心。根據決策值確定聚類中心點之后，SNN-DPC 算法對未分配的點分為兩類考慮，確定的從屬點與可能的從屬點。

定義6（確定的從屬點與可能的從屬點）滿足不等式（7）所示的條件，就是確定的從屬點，否則就是可能的從屬點。假設點xi已經被安排到一個簇中，xj還沒有被安置，如果點xj滿足不等式（7），那么xj不可避免地屬于xi所在的簇。換句話說，xi和xj各自的K鄰域中至少一半是共享的，兩點才有可能成為同一個簇的點。

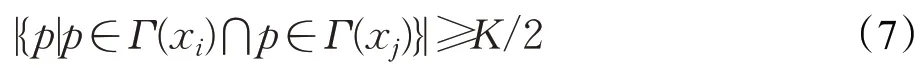
除了定義上的差異外，確定的從屬點和可能的從屬點之間的另一個區別是，在非極端情況下，每個點都可能同時從屬于多個聚類，卻不可避免地只能從屬于一個簇。

2 基于共享鄰居的改進聚類方法

SNN-DPC算法在計算樣本點間相似度時采用的是歐式距離代表數據點之間的相似程度，距離越大，表示相似性程度越低，因此不能利用相似度矩陣直接進行計算。本文首先通過轉換函數，將相似度矩陣轉變為距離矩陣，再使用SNN-DPC算法，可以提高聚類算法對各種相似度矩陣的適應度。聚類可以對相關性較強的樣本進行劃分，而離群點檢測可以對相關性非常弱的樣本點進行分類，聚類與離群點分析可以形成一種互補關系。SNN-DPC 算法中沒有對離群點進行分析，在處理確定的從屬點與可能的從屬點時力求每一個點都可以安排到一個確定的簇，因此不可避免地會受到離群點對聚類結果的影響。本文通過將離群點檢測算法與SNN-DPC算法相結合，先對數據集中的離群點做“高亮”處理，對剩下的點進行聚類，可以提高聚類的準確性與快速性，達到較好的聚類效果。另外，檢測出的離群點也可做單獨分析。

2.1 相似度矩陣轉變為距離矩陣

本文采用的原始數據集為某校園無線網絡中記錄的用戶真實軌跡數據。數據集中將包含的校園全區域范圍內的各地點分別用數字進行編號。用戶某天的時空軌跡序列如表1所示，其中l表示用戶所在區域編號，t表示用戶在該地的網絡登錄時間，m為用戶總量，W1,W2,…,Wm分別表示各用戶軌跡序列中的登錄記錄總數。

表1 用戶時空軌跡數據集Table 1 User spatial-temporal trajectory dataset

基于無線網絡中時空軌跡的數據特點，在分別計算不同用戶之間軌跡的時間相似性和空間相似性后，引入連續因子優化空間相似性度量，結合軌跡的時間維度與空間維度求得用戶之間的軌跡相似度信息[10]。

相似度信息包括時間相似性與空間相似性。

對于整體軌跡序列而言，兩軌跡中時間距離小的軌跡點越多，說明相遇次數越多，軌跡整體的時間相似性越高。采用最短時間距離（shortest time distance，STD）[11]模型計算時間相似性。

假設存在兩個用戶ui和uj，其時空軌跡序列分別為Ri={ri,1,ri,2,…,ri,x,…,ri,Wi}和Rj={rj,1,rj,2,…,rj,y,…,rj,Wj}。并假設存在兩個軌跡點ri,x(li,x,ti,x)和rj,y(lj,y,tj,y)，其時間距離記為Dis(ri,x,rj,y)，如式（8）所示：

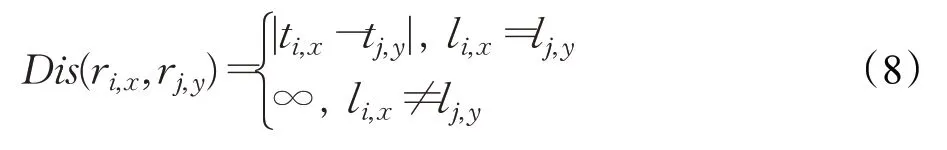
最短時間距離定義為軌跡Rj中所有軌跡點中與軌跡點ri,x時間距離最小的值，表示如式（9）：

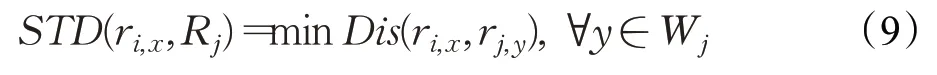
軌跡Ri對于軌跡Rj的時間相似性可以近似為軌跡Ri中所有軌跡點與Rj中對應STD 匹配軌跡點的時間相似性總和，記為Cor(Ri,Rj)，表示為式（10）：

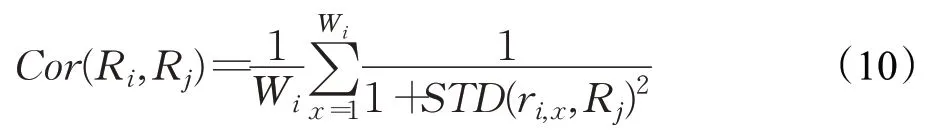
由于STD模型的計算結果不具有對稱性，兩軌跡之間的時間相似性表示為式（11）：

空間相似性信息利用最長公共子序列（longest common subsequences，LCSS）[12]算法，尋找兩個給定序列的公共子序列中最長的子序列。

軌跡Ri和軌跡Rj的空間相似性由LCSS序列的長度分別占兩條軌跡長度比例的平均值與連續因子共同決定：

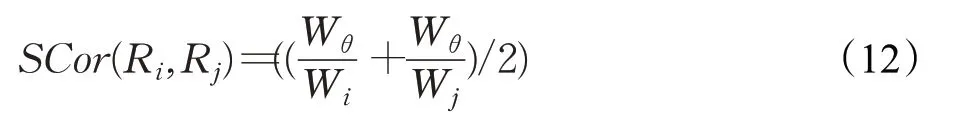
其中，Wθ表示LCSS序列的長度。

用戶相似性可以通過軌跡段的時空相似性得到，用式（13）表示：

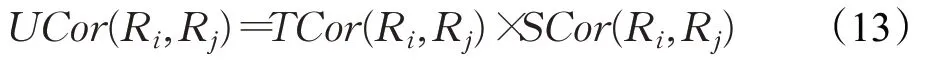
相似度矩陣用S表示，如式（14）所示：

其中，sij表示用戶i和用戶j之間的相似度，即式（13）中的UCor(Ri,Rj)，0 ≤sij≤1。矩陣的對角線元素為1。

由于相似度矩陣與距離矩陣負相關，即相似度矩陣中的值越大，距離矩陣中的值應該越小。因此，采用如式（16）所示的轉換函數將相似度矩陣轉換為距離矩陣。

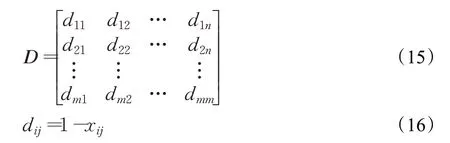
其中，i=1,2,…,m，j=1,2,…,m，dij表示用戶i和j之間的距離，D表示距離矩陣。

2.2 基于離群點檢測的SNN-DPC聚類算法

為了減少離群點對算法的影響，首先需要確定數據集中的離群點并且移除它們。許多真實世界的數據集展示了一個非常復雜的結構，在實際應用中，通常會按照實際情況選擇對應的離群點數據挖掘算法。本文針對SNN-DPC 算法提出兩種離群點檢測算法，一種算法是基于局部密度離群點檢測的SNN-DPC 算法，簡稱RSNN-DPC 算法，該算法是利用SNN-DPC 算法本身計算的局部密度值，設定閾值范圍，尋找離群點。另一種算法是基于LOF 離群點檢測的SNN-DPC 算法，簡稱LSNN-DPC 算法，其是將LOF 算法與SNN-DPC 算法相結合，減少實驗輸入參數并去除離群點的影響，成為新的去除離群點的聚類算法。

2.2.1 基于局部密度離群點檢測的改進算法（RSNN-DPC）

在SNN-DPC 聚類算法中，有兩個重要指標可以表征樣本點的密度情況，即局部密度ρ和最近距離δ，通過第1 章對SNN-DPC 算法的分析，最近距離是根據局部密度進行定義的，因此可以通過局部密度來表征樣本點的密度情況。如果一個對象的局部密度相對于其相鄰對象的密度要低得多，那么這個對象很有可能就是一個離群值。

在SNN-DPC算法中，局部密度ρ具有以下特性[13]：

（1）當鄰居數K較小時，點xi與其鄰居xj之間的共享鄰居數較小，同時點xj與點xi之間的距離也較近，此時，K反映了點xi較小鄰域內的局部密度。相反，當K較大時，點xj與點xi之間的距離較遠，它反映了xi的較大鄰域內的局部密度。低密度簇中的點之間的距離較大，因此K的變化將對低密度簇產生更大的影響。

（2）當|SNN(xi,xj)|恒定時，如果點xi和點xj到它們的每個共享鄰居的距離都很小，則ρi較大。換句話說，如果點xi和點xj之間的距離很小，并且每個共享的相鄰點到xi和xj的距離也很小，那么點xi的密度就很大。因此，空間中距離數據點xi越近的點對ρi的貢獻越大。

通過對局部密度的分析可知，局部密度ρ不僅利用距離信息，而且還通過共享最近鄰數SNN 獲得有關聚類結構的信息，充分揭示了點與點之間的內在關系。在這種情況下，如果局部密度值為0，說明數據集X中與之相關的所有點SNN相似度為0，可能原因有以下兩點：

（1）該點獨立于其他各點，與數據集中剩余點沒有共享鄰居點，即SNN為0。

（2）點xi和xj到它們所有共享鄰居的距離接近于無窮

因此，可以將局部密度ρi作為離群點的一個判斷條件，通過判斷局部密度是否為0 選擇離群點并刪除，再進行接下來的聚類。算法的具體步驟用算法1 和算法2表示，其中算法1表示的是RSNN-DPC算法的整體過程，算法2表示的是在確定聚類中心后分配確定的從屬點與可能的從屬點的具體算法步驟。

算法1基于局部密度離群點檢測的改進算法（RSNN-DPC）

輸入：相似度矩陣X，鄰居數目K，聚類數NC。

輸出：聚類結果Φ={C1,C2,…,CNC} ，離群點集合Ψ={ψ1,ψ2,…}。

步驟1對相似度矩陣X進行預處理，根據轉換式（16），計算距離矩陣D。

步驟2根據式（2）計算相似性矩陣Sim(xi,xj)。

步驟3根據式（3）計算局部密度ρ。

步驟4篩選出局部密度ρi=0 的數據點作為離群點，輸出離群點集合Ψ={ψ1,ψ2,…}，并將數據集中的離群點刪除，對剩余樣本聚類。

步驟5根據式（4）、（5）計算最近距離δ。

步驟6根據式（6）計算所有點的決策值并按降序排列，得到排序后的γ′。

步驟7根據聚類個數NC，選擇γ′最大的前NC個點確定為聚類中心，由此產生聚類中心數據集Center={c1,c2,…,cNC}。

步驟8根據算法2，分配確定的從屬點和可能的從屬點，并將從屬點歸類到對應的集合中，得到聚類結果Φ。

算法2分配確定的從屬點和可能的從屬點

輸入：聚類中心數據集Center={c1,c2,…,cNC}, 鄰居數目K，距離矩陣D。

輸出：最終聚類結果Φ={C1,C2,…,CNC}。

步驟1初始化隊列Q，將聚類中心Center中所有點置入隊列Q。

步驟2將隊列Q中第一個點xa從隊列中取出，根據距離矩陣D查找點xa的K個最近鄰，定義最近鄰集合為Ka。

步驟3依次選擇最近鄰集合中的未分配點x′∈Ka x′∈Ka，如果x′滿足條件（7），則將數據點x′歸類到xa所在的簇中，并將x′添加至隊列Q尾部，作為已知分配情況的樣本點；否則x′為可能的從屬點，暫時無法分配簇集，繼續選擇最近鄰集合Ka中的下一個點判斷分配情況，Ka中所有樣本點判斷完畢后轉步驟2，進行隊列Q中下一個確定的從屬點的分配。

步驟4當Q=?時，代表所有確定的從屬點已經分配完畢，數據集中剩余點為可能的從屬點，接下來對可能的從屬點進行分配。

步驟5找到未分配的可能的從屬點并重新編號。定義一個矩陣M，行表示未分配點的編號，列表示簇序號。

步驟6計算每一個未分配的點的鄰居中屬于各個簇的鄰居數，并將其寫入分配矩陣M的對應簇的列元素中。

步驟7尋找中M每一行元素的最大值Mimax，用最大值所在的簇表示該行未分配點i的簇。分配完成后更新矩陣M，直到所有點均被分配。

步驟8輸出最終聚類結果Φ={C1,C2,…,CNC}。

2.2.2 基于LOF離群點檢測的改進聚類算法（LSNN-DPC）

2.2.1小節采用局部密度來表示樣本點的密度情況，可以根據樣本點局部密度的差異檢測出密度明顯異常的點，但是由于局部密度受到鄰居數的影響較大，當鄰居數取值不合理時，可能檢測不出離群點。在眾多的離群點檢測方法中，LOF（local outlier factor）方法[14]是一種典型的基于密度的離群點檢測方法，此方法能有效識別局部離群點和全局離群點，因此在離群點檢測問題中廣泛應用。其主要定義如下：

定義7（ε-鄰域Nε(i)和數據點xi的k-距離Nk(i)）ε-鄰域定義為與數據點的距離小于ε的數據點集合。數據點的k-距離定義為與數據點的距離小于k_dist(i)的數據點集合。ε-鄰域用于確定數據點的密度特征比較范圍，即每個數據點的密度特征與其ε-鄰域內的數據點比較。同樣，k_dist(i)表示數據點xi與距其第k近的數據點的距離，具體定義如式（18）所示：

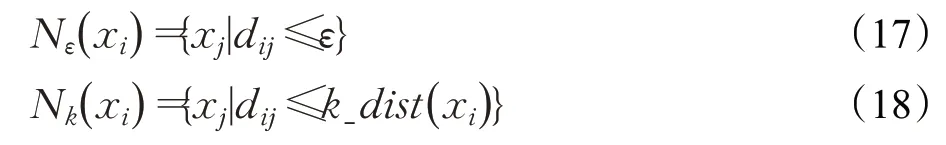
其中，k為自然數。

定義8（數據點xi的核心距離cd(xi)）當xi的ε-鄰域內數據點數目大于MinPts時，xi的核心距離定義為xi的MinPts-距離，否則定義為0，具體如式（19）所示：

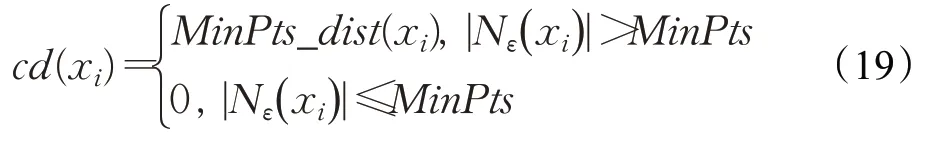
其中，MinPts為給定自然數。

定義9（數據點xi關于xj的可達距離rd(xi,xj)）當xi的ε-鄰域內數據點數目大于MinPts時，xi關于xj的可達距離定義為xi的核心距離與兩點之間真實距離的最大值，否則不作定義。也就是說，數據點xi關于xj的可達距離至少是xi的核心距離，或者是兩點之間的歐式距離。具體定義如式（20）所示：

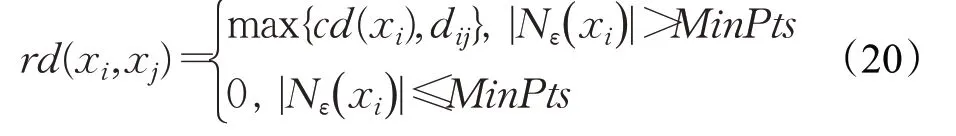
定義10（數據點xi的局部可達密度lrd(xi)）局部可達密度定義為數據點xi的MinPts-鄰域內數據點個數和xi與其鄰域內其余數據點可達距離之和的比值，表征了數據點xi的局部密度。局部可達密度值越大，局部區域點的分布就越密集。定義如式（21）所示：

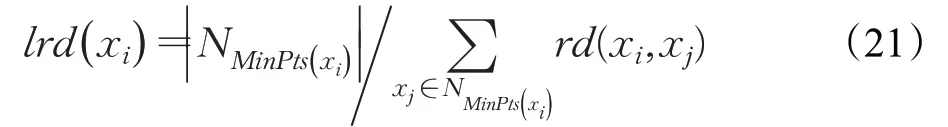
定義11（數據點xi的離群因子LOF(xi)）數據點xi的離群因子定義為xi的MinPts-鄰域內數據點與xi點局部可達密度的平均比值。數據點的離群因子值越高，說明xi點與其鄰域內數據點密度特征差異越顯著，其成為離群點的可能性也就越大。

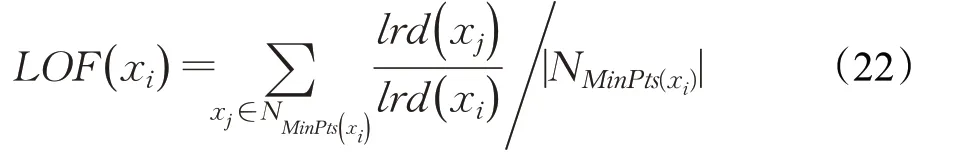
xi的離群因子LOF(xi)表示的是一種密度對比，表示數據點與整體的一種密度差異。若LOF 值遠遠大于1，表示該點的密度與數據的整體密度差異較大，則認為該點為離群點。假如LOF值接近于1，表示該點與整體的差異較小，因此可認為該點為正常點。

為直觀表示說明，隨機生成一個100×2 的數據集，指定第99 個和第100 個數據為離群數據。圖1 用二維坐標圖的形式說明了原始數據的分布情況，可以看出，大部分數據分布在一個1×1的正方形區域內，而第99個點和第100 個點遠離樣本集合，明顯為離群點。圖2 展示了通過LOF算法計算的100個樣本點的離群度。

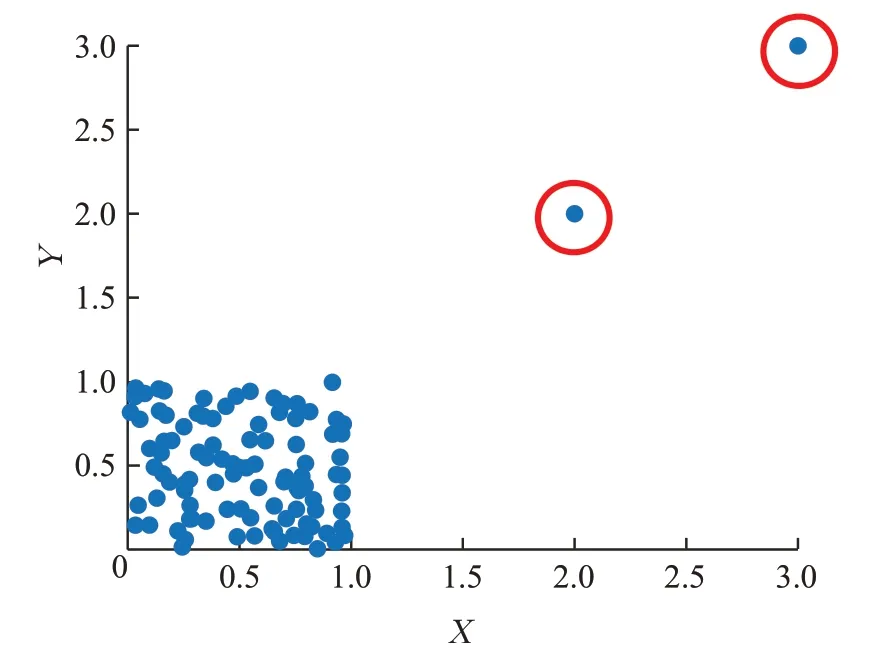
圖1 100個隨機數據分布二維示意圖Fig.1 Two-dimensional schematic diagram of 100 random data distribution

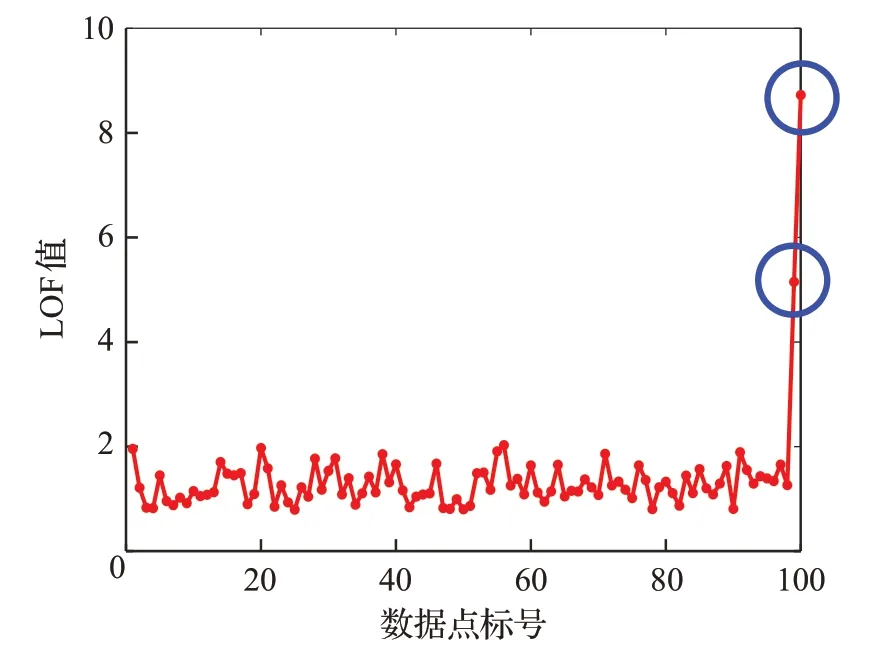
圖2 各數據樣本點LOF值比較Fig.2 Comparison of LOF value of each sample point

大部分LOF值在1附近波動，表示大部分點密度與整體密度差異不大，而99 和100 個點的LOF 值遠大于1，接近5和8，表示這兩點的密度與整體密度差異較大，因此可以認為這兩點為離群點，這與之前的假設也是契合的。

在現實場景中，數據分布往往是非均勻的。LOF算法可以很好地解決基于距離和統計離群檢測方法無法檢測局部離群點的問題[15]，但其算法本身也存在一些不足：

對于分布較密的數據集，如果選擇的MinPts值較小，可能會出現部分對象的MinPts-距離為空值，導致其MinPts-鄰域內的所有點到該點的距離都為0，在計算可達距離時會出現分母為0，導致LOF值無窮大的現象，會導致局部異常因子運算異常。

LOF 算法的性能受參數MinPts影響較大，對于參數值的確定，需要一定的鄰域知識，這使得算法的難度加大。而且人工干預和經驗值的參與也會直接影響到算法在離群檢測中的性能。

基于LOF算法的兩個不足，本文提出利用SNN-DPC中定義的鄰居數K代替MinPts-鄰域中MinPts值的改進方法。由于SNN-DPC 中定義的鄰居數是與某點xi距離最近的K個點的個數，MinPts-鄰域中的MinPts表示的含義與鄰居數K相近，因此用鄰居數K來替換鄰域值MinPts是合理的。將LOF 算法與SNN-DPC 算法相結合，此時只需要設置一個鄰居數K即可，有效減少了參數的輸入個數，降低了獲取參數的困難性。同時，由于定義的鄰居數不可能為0，也可以杜絕算法在運行時出現分母為0的運算錯誤。

LSNN-DPC的具體算法步驟用算法3表示，其中包含的算法2在2.2.1節已作說明。

算法3基于LOF離群點檢測的改進算法（LSNN-DPC）

輸入：相似度矩陣X，鄰居數目K，聚類數NC。

輸出：聚類結果Φ={C1,C2,…,CNC} ，離群點集合Ψ={ψ1,ψ2,…}。

步驟1對相似度矩陣進行預處理，根據轉換公式（16），計算距離矩陣D。

步驟2根據離群因子計算式（22），計算各樣本點的LOF 值，找到超出閾值范圍的點，輸出離群點集合Ψ={ψ1,ψ2,…}，并將數據集中的離群點刪除，對剩余樣本點進行聚類。

步驟3根據式（2）計算相似性矩陣Sim(xi,xj)。

步驟4根據式（3）計算局部密度ρ。

步驟5根據式（4）、（5）計算最近距離δ。

步驟6根據式（6）計算所有點的決策值并按降序排列，得到排序后的γ′。

步驟7根據聚類個數NC，選擇γ′最大的前NC個點確定為聚類中心，由此產生聚類中心數據集Center={c1,c2,…,cNC}。

步驟8根據算法2，分配確定的從屬點和可能的從屬點，并將從屬點歸類到對應的集合中，得到聚類結果Φ。

3 實驗分析

為了驗證算法的有效性及可行性，本文選擇真實校園無線網絡中記錄下的數據集產生的相似度矩陣轉化后距離矩陣的Stu_500 和Stu_2000 進行驗證與評估。由分析可知，距離矩陣是通過最短時間距離子序列軌跡相似性度量模型得到的相似度矩陣通過轉換函數得到的。兩個數據集均由山東某高校2019 年9 月1 日至2019 年9 月30 日共一個月的學生軌跡記錄以及學生相關信息組成。表2 說明了兩個數據集包含學生種類的大致情況。

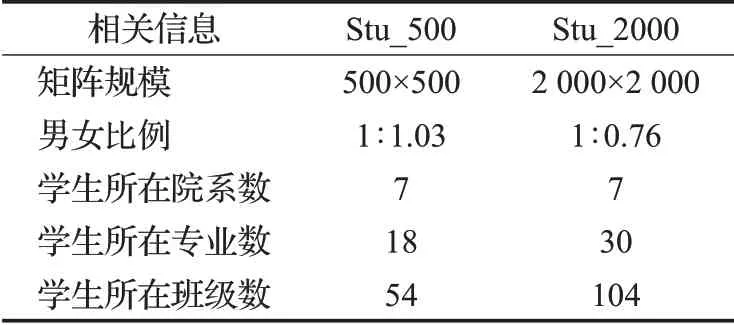
表2 數據集情況描述Table 2 Description of dataset

表3說明了本次實驗的硬軟件環境及開發工具。

表3 實驗環境Table 3 Experimental environment

為量化評價算法的檢測結果，需要使用評價指標表示聚類效果的優劣程度。校園無線網絡數據集是無標簽的，因此不能依靠外部指標，只能通過內部指標來判斷聚類形成的簇間距離和簇內距離大小。一般來說，聚類的目標是使得簇間距離增大而簇內距離減小，通過對簇內距離和簇間距離不同角度的組合判斷，提出以下幾種評價指標。評價指標根據趨勢分為兩類：一類指標數值越大，聚類效果越好，稱為正相關指標；另一類指標數值越小，聚類程度越高，稱為負相關指標。正相關指標包括鄧恩指數（Dunn validity index）[16]、輪廓系數（Silhouette index，Sil）[17]；負相關指標包括緊密性程度（compactness，CP）[18]、戴維森堡丁指數（Davies-Bouldin index，DBI）[19]。各個指標都能夠從一個方面對聚類結果進行一定的評估，但是也都存在一定的局限性，因此，應將各種內部指標結合起來綜合評估，而不應該因為一個評價指標沒有得到較好的評價結果而否定聚類效果[20]。

3.1 數據集預處理

學生相似度矩陣中存在數據缺失或者不完整的部分，會影響數據的正確性繼而不利于聚類，為了清除數據缺失等問題的影響，同時提高數據挖掘的質量，需要對數據進行預處理操作。

缺失的數據一般指的是沒有采集到的數據或者是無限小的無效數據，對學生軌跡相似度的缺失處理分為兩種情況。對相似度矩陣中全零行或者全零列判斷為學生軌跡數據整體信息缺失，對于這部分數據記錄其學生編號，采用整體賦值的辦法處理。而對相似度矩陣中某一行或一列有部分數據缺失，即此人與其他大部分人有相似度，僅與小部分人相似度為0，對這部分數據的處理與缺失值處理相同，當相似度矩陣轉化為距離矩陣時賦一個比較大的數據，表示此人與這部分人相似度極低。

3.2 算法參數的選擇與分析

SNN-DPC算法中提出采用決策圖的方式確定聚類數。決策圖是將γ值降序排列后，以數據點個數為橫坐標，以排序后的γ′值為縱坐標。γ′值越大表示該點的局部密度ρ和最近距離δ越大，即越有可能成為聚類中心點。實驗中的決策圖，即Stu_500 數據集與Stu_2000數據集得到的排序后的γ′值如圖3和圖4所示。

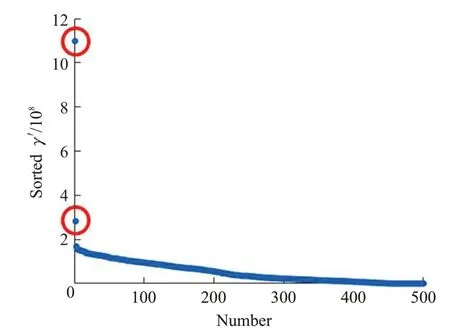
圖3 Stu_500決策圖Fig.3 Decision diagram of Stu_500

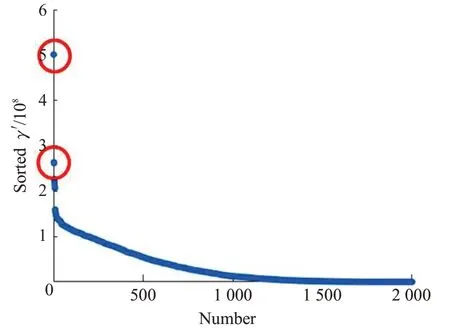
圖4 Stu_2000決策圖Fig.4 Decision diagram of Stu_2000

可以看到在決策圖中，γ′值比較大且遠大于剩余點的γ′值的點均有兩個，已用紅色圓圈在圖中標明。

因此以聚類數為2（NC=2）為例說明使用RSNNDPC與LSNN-DPC算法聚類后內部指標的差異。

明確聚類簇數后，本實驗可調整的參數僅包含鄰居數K。選擇合適的鄰居數范圍能夠有效減少尋找最優鄰居數的時間，因此先對各個內部指標隨鄰居數變化情況進行預實驗，即令鄰居數K從小到大變化，觀察各指標變化情況。對于鄰居數范圍選擇的下限，考慮到若鄰居數目過少，某些數據集中點密度過于稀疏，不具備相似性，而且對于某些數據集，可能因為K過小導致錯誤，因此下限確定為5。

圖5 和圖6 分別表示Stu_500 和Stu_2000 數據集Sil、DBI 兩個指標的變化情況，圖（a）均為Stu_500 數據集，其K值從5到200變化，圖（b）對應Stu_2000數據集各指標隨鄰居數增加的變化情況，其K值從5到500變化。以Stu_500 數據集為例分析，Sil 指標越大，表示聚類效果越好。由圖5（a）可知，當鄰居數較少時，Sil指標的震動幅度較大，并且出現了多個峰值點，隨后，當鄰居數K ＞50 時，Sil數值較平緩，意味著選擇鄰居數范圍為[5，50]就足以找到最優鄰居數。

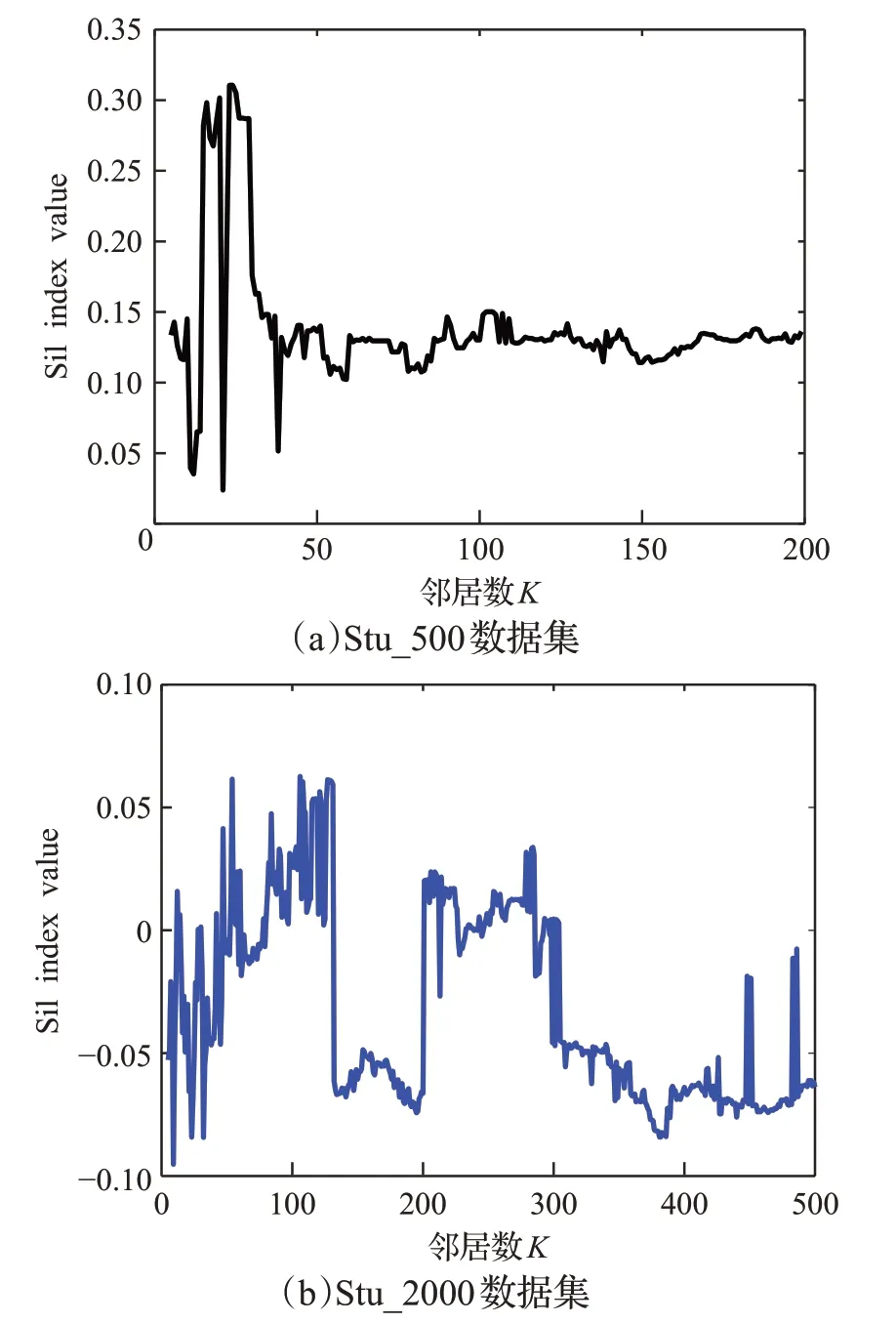
圖5 Sil指標隨鄰居數增加的變化Fig.5 Change of Sil index as number of neighbors increases

DBI指標值越小，表示聚類效果越好。觀察圖6（b）可以發現，當鄰居數接近為10時，DBI達到一個最小值，可見此時對應的K鄰居數為DBI 指標最優時的鄰居數，隨著鄰居數的增加，DBI的值越來越大，后期穩定在一個比較高的數值，根據趨勢分析，不能再出現最小值點，因此，選擇鄰居數范圍為[5，60]足以找到使得DBI達到最優時的鄰居數。

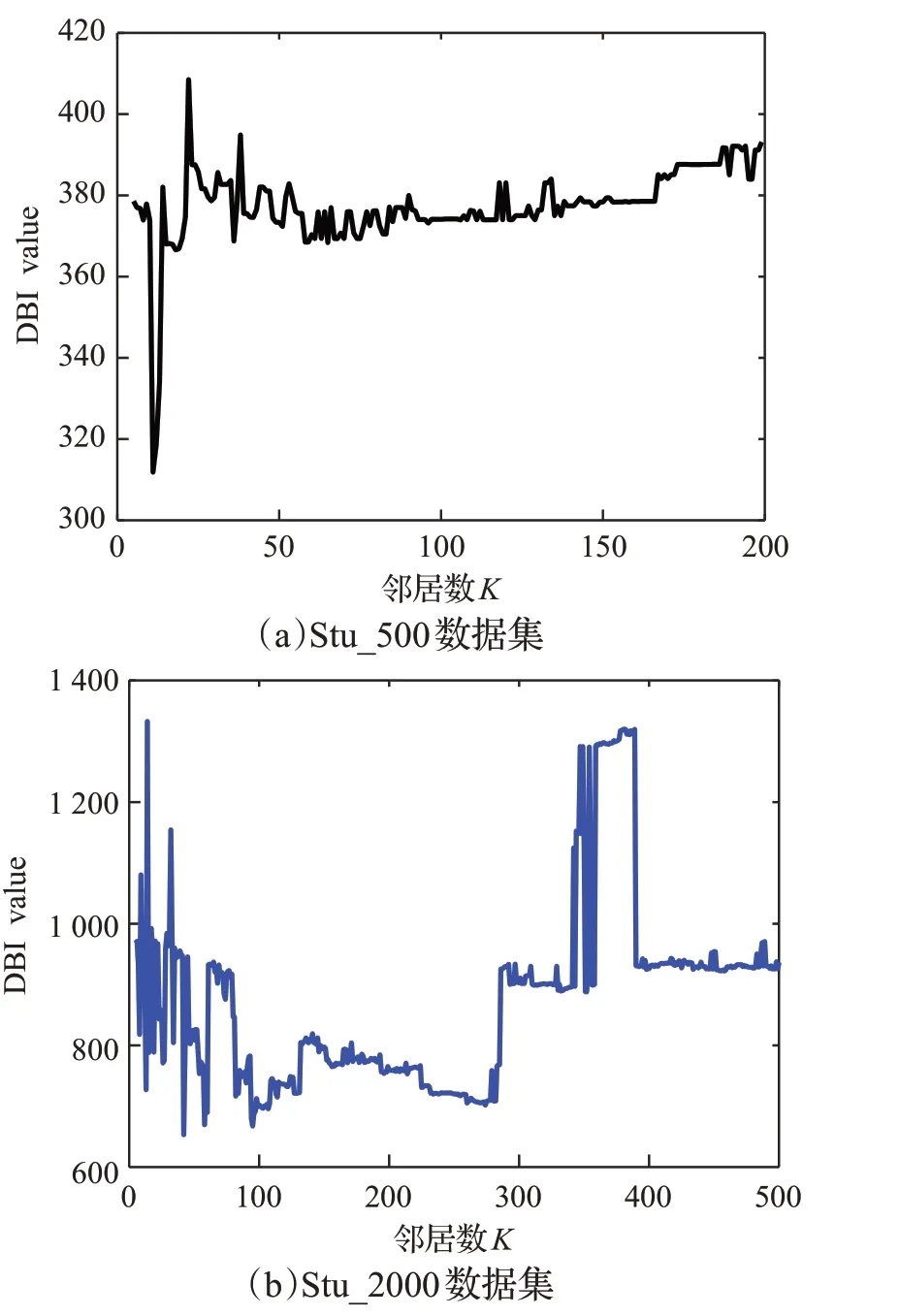
圖6 DBI指標隨鄰居數增加的變化Fig.6 Change of DBI value as number of neighbors increases

綜合上述分析，對Stu_500 矩陣，鄰居數K的取值范圍確定為[5，60]即可，后續實驗操作也將基于這個實驗范圍進行內部指標分析。運用同樣的方法，對Stu_2000 矩陣進行鄰居數K的取值判定，發現取值范圍為[5，300]可以滿足選擇最優指標的最低要求。

根據2.2.2 節對LOF 算法的分析，若離群因子值接近于1，表示樣本點與整體的差異較小，因此可認為其為正常點，否則視為離群點。本文設置閾值為2，若計算出LOF≥2，則認為該樣本點為離群點。

若分開使用LOF 算法和SNN-DPC 算法，需要設定LOF算法的MinPts距離，為保證實驗的統一性，采用距離樣本點第10 遠的樣本點（即MinPts=10）距離作為LOF算法的MinPts距離。

3.3 離群點檢測數量的對比實驗

本文采用兩種離群點檢測算法與SNNDPC 算法相結合，去除離群點的影響，增加聚類結果的可信度。離群點檢測在聚類之前進行，因此不需要指定明確的聚類簇數，兩種離群點檢測算法的變量僅為鄰居數K。本節探討隨著鄰居數K的增加，RSNN-DPC 和LSNN-DPC兩種算法在檢測離群點個數方面的變化情況。

圖7（a）表示Stu_500矩陣，鄰居數K從5到60變化時，離群點數量變化情況。可以發現，隨著鄰居數的增加，LSNN-DPC算法得到的離群點個數，除了K ＜6 時離群點數量較大，剩余情況檢測出的離群點數量基本保持平穩，可以說明該算法的穩定性較高，不會隨著鄰居數的增大而產生太大變化。而通過RSNN-DPC尋找到的離群點數目受到鄰居數的影響較大，當鄰居數較小時，離群點數量很大，隨著鄰居數目的增加，離群點的個數呈現出單調遞減的趨勢，但是在K ＞35 時，隨著鄰居數的增大得到離群點的數量穩定。

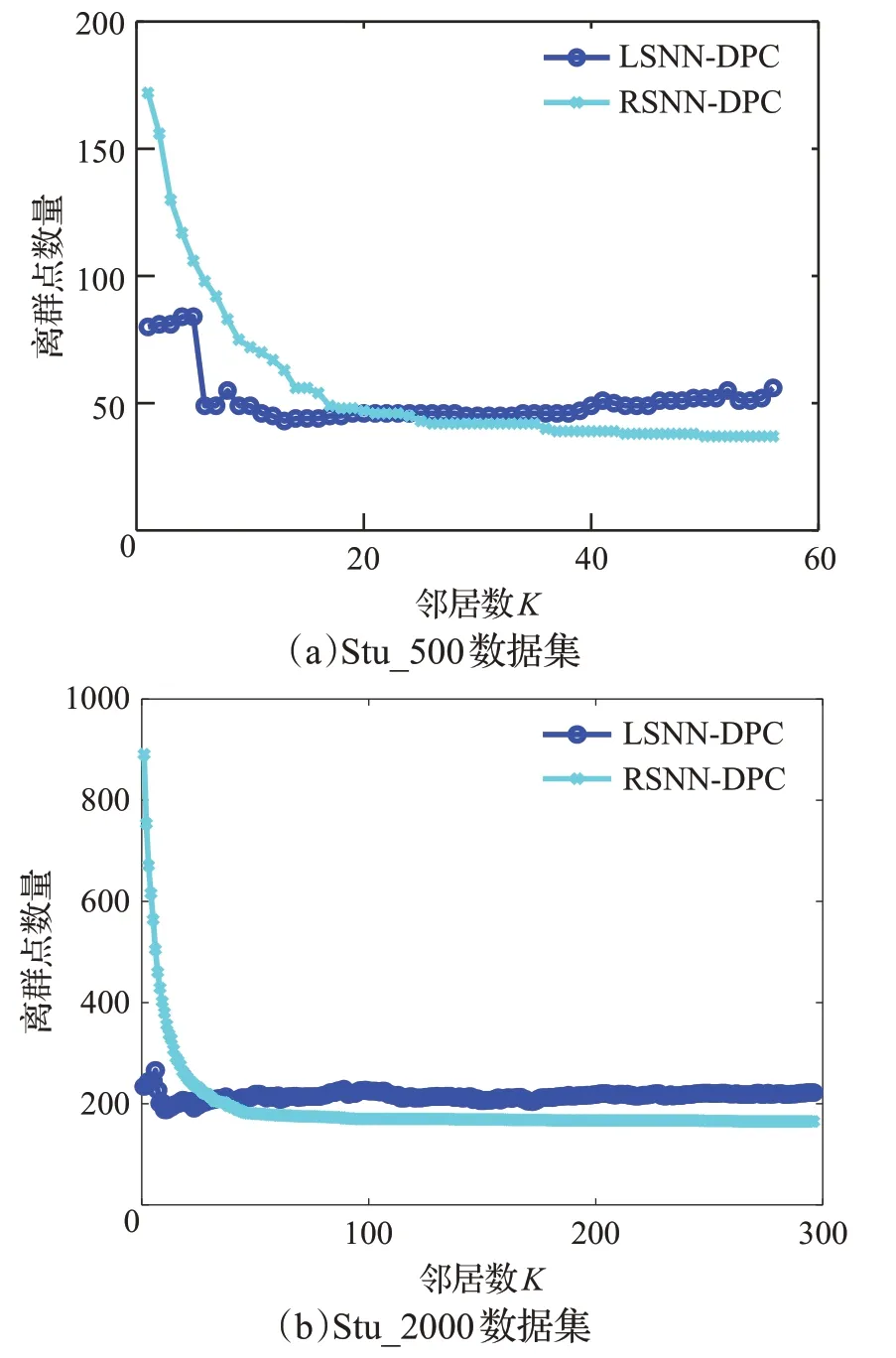
圖7 離群點數量變化Fig.7 Change in number of outliers

圖7（b）表示Stu_2000矩陣，當鄰居數K從5到300變化時，兩種算法得到的離群點數量變化情況。可以發現，隨著鄰居數K的增加，LSNN-DPC算法得到的離群點數目基本保持穩定，而通過RSNN-DPC 算法得到的離群點數量呈遞減趨勢，兩者最終判斷的離群點數量接近一致。

通過兩個數據集的對比發現，隨著數據點總量的增加，LSNN-DPC檢測出的離群點數量更為統一。RSNNDPC前期離群點數量變化較大，后期離群點數量保持穩定。兩者最終判斷的離群點個數趨于相同。

3.4 聚類內部指標的對比實驗

通過比較聚類內部指標的具體數值，可以推斷出各個算法聚類的優劣。本文用Stu_500 和Stu_2000 兩個校園無線網絡軌跡距離矩陣進行實驗，在計算各指標時，將每個離群點單獨設置為一類，聚類中心為離群點本身。例如假設LSNN-DPC算法得到h個離群點，那么在計算各指標時，計算的是h+NC個聚類中心與其對應點之間的關系，這樣可以保證各個算法計算得到的指標值考慮到所有樣本點，而不是完全不考慮離群點后指標的變化。

表4至表6分別表示使用Stu_500矩陣，令K從5到60變化，每一種算法當CP指標、DBI指標、Dunn指標分別最優時，對應的鄰居數K及其對應的CP指標、DBI指標、Dunn 指標、Sil 指標值。SNN-DPC 行表示原SNNDPC 算法未去除離群點的影響時聚類得到的各指標，LSNN-DPC行代表LSNN-DPC算法得到的各指標情況，RSNN-DPC行表示RSNN-DPC算法得到的各指標對應情況，LOF+SNN-DPC 行代表通過單獨使用LOF 算法（K=10），去掉離群點后再使用SNN-DPC 聚類算法得到的各指標數值。

表4 CP指標最優時對應其余各指標值（Stu_500）Table 4 Other index values corresponding to optimal CP index（Stu_500）

表6 Dunn指標最優時對應其余各指標值（Stu_500）Table 6 Other index values corresponding to optimal Dunn index（Stu_500）

通過對表格的分析可知，最優指標集中出現在LSNN-DPC 和RSNN-DPC 中，說明文中所提出的兩種基于離群點檢測的SNN-DPC聚類算法在提高聚類效果上有一定的優勢。其中LSNN-DPC 的CP 指標表現最優，說明使用LSNN-DPC得到的類簇，類內距離近，簇內聚合度最高。LOF+SNN-DPC 算法雖然能在一定程度上減少離群點對聚類效果的影響，但是由于參數K固定，并且參數的取值困難，導致參數取值不合適或者離群點判斷存在偏差，使聚類結果劣于LSNN-DPC 和RSNN-DPC。

表7 至表9 表示的是Stu_2000 矩陣聚為兩類時，當K從5 到300 變化時，每一種算法得到的聚類結果中，CP、DBI、Dunn指標最優的鄰居數對應的其余各指標數值。表格各行的含義與Stu_500數據集定義相同。

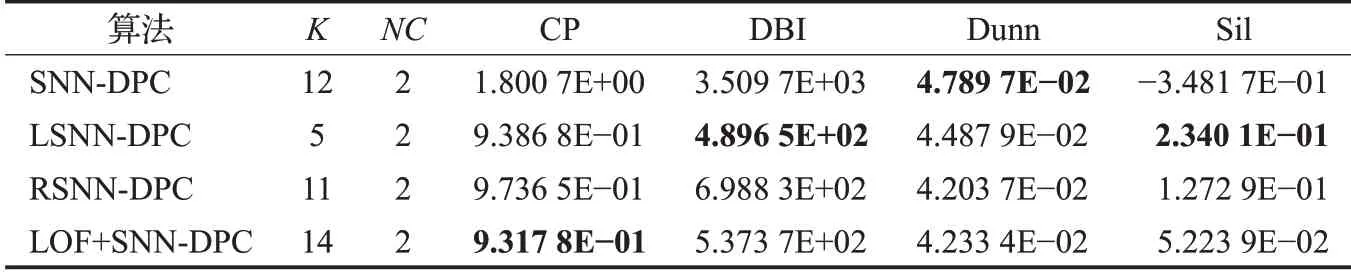
表7 CP指標最優時對應其余各指標值（Stu_2000）Table 7 Other index values corresponding to optimal CP index（Stu_2000）

表9 Dunn指標最優時對應其余各指標值（Stu_2000）Table 9 Other index values corresponding to optimal Dunn index（Stu_2000）

通過對表格的分析可以發現，針對CP 指標來說，LOF+SNN-DPC 算法是最優的，說明針對Stu_2000，令MinPts=10 能夠單獨使用LOF算法找到對聚類影響最大的離群點。盡管LSNN-DPC 和RSNN-DPC 在CP 指標上的表現差強人意，但是樣本點規模的擴大沒有明顯影響到改進后算法的聚類效果，LSNN-DPC 算法和RSNN-DPC 的大部分指標均優于SNN-DPC 和LOF+SNN-DPC。也就是說，兩種改進算法對數據集中數據量增加的魯棒性較高，進一步驗證了基于離群點檢測的改進SNN-DPC算法在無線網絡軌跡相似度數據集上的可行性。

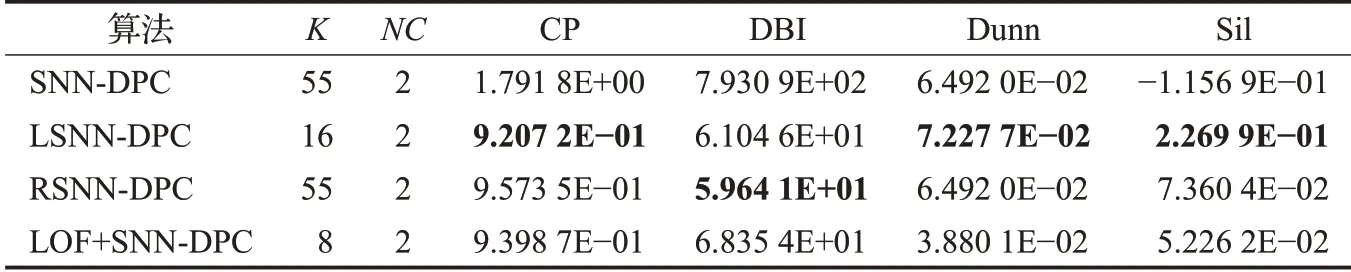
表5 DBI指標最優時對應其余各指標值（Stu_500）Table 5 Other index values corresponding to optimal DBI value（Stu_500）

表8 DBI指標最優時對應其余各指標值（Stu_2000）Table 8 Other index values corresponding to optimal DBI value（Stu_2000）

另外，以Stu_500矩陣為例，通過上面數據的分析，當NC=2 ，鄰居數K=37 時，比較LSNN-DPC 算法、RSNN-DPC 算法與未去除離群點的SNN-DPC 算法，對比結果如表10所示，其中聚類中心點8，279表示聚類中心點為編號為8和編號為279的兩個點。

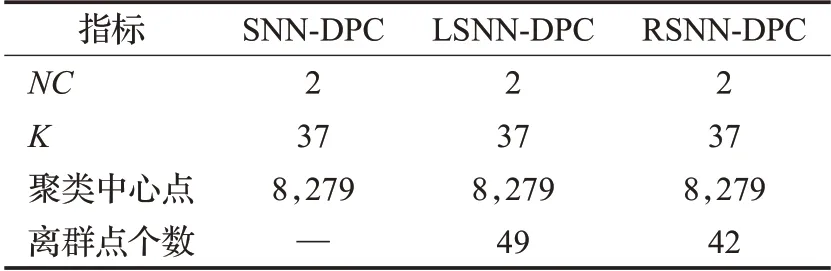
表10 聚類結果對比Table 10 Comparison of clustering results

可以看到，LSNN-DPC 和RSNN-DPC 兩種算法不會影響聚類中心點的選取，只會去除邊緣的離群點，避免離群點對整體聚類效果的影響，優化聚類效果。因此，基于離群點檢測的SNN-DPC 算法可以應用于此類基于校園無線網絡軌跡數據的聚類研究中。

4 結束語

現有聚類算法大多數是利用歐氏距離、馬氏等距離來定義相似度，也就是說，大部分聚類算法直接利用距離矩陣對數據集進行處理，而無法直接處理相似度矩陣。針對此問題，本文在校園無線網絡時空軌跡用戶相似性度量研究的基礎上，研究了聚類算法應用于相似性矩陣上的可能性，將相似度矩陣轉化為距離矩陣，再通過基于密度的聚類算法進行聚類分析。其次，由于大部分聚類算法未考慮到離群點對聚類結果的影響，本文提出了兩種基于離群點檢測的SNN-DPC 聚類算法，其中LSNN-DPC檢測出的離群點數目較為穩定，RSNN-DPC算法檢測出的離群點數目前期變化較大，后期趨于穩定。兩種改進算法一方面可以減少輸入實驗參數，另一方面在剔除離群點的影響后進行聚類，可以提高聚類的聚合程度。通過實驗驗證，LSNN-DPC 和RSNN-DPC兩種改進聚類算法各項指標整體優于SNN-DPC算法和LOF+SNN-DPC 算法。將改進后的算法應用到實際校園無線網絡軌跡行為特征的挖掘中，可以聚類校園中大部分用戶的軌跡數據，通過分析大部分用戶的行為特征，有利于分析學生之間的關聯性，可以為校園建設方案提供可靠依據。另外，對于算法得到的離群點，也可以找到相應的用戶對其進行處理，及時發現學生的異常，有針對性地對不同屬性的學生進行管理。