基于譜函數二階導數的波達方向估計

潘秋甫 孫 曼 余小玲

(四川大學電氣工程學院 四川 成都 610065)

0 引 言

DOA(信號波達方向估計)是信號處理領域的重要研究方向[1-2]，尤其是在短波測向[3]、軍事對抗、雷達探測、聲吶和移動通信等方面都有著廣泛的應用[4]。隨著電子戰對作戰隱蔽性及作戰精密度要求逐漸增強，雷達等主動測向技術因主動發射電磁波進行測向，容易被捕捉信源方向，大大降低了作戰安全性，因此高精度高分辨率的被動測向技術成為軍事測向的發展趨勢[5]。

基于多重信號分類的高分辨空間譜測向算法克服了傳統比幅比相式測向機制[6]的缺點，可對同信道中多個信號進行超分辨測向，實現波束合成[7]和同頻干擾檢測，以其卓越的測向性能得到了廣泛的關注和研究。文獻[8-10]通過降低MUSIC算法的計算復雜度來達到較好的工程實用價值。然而，這類算法對計算量降低效果有限，且是以降低計算精度為前提的。文獻[11-13]提出將現代信號處理方法作用于空間譜估計，使得信號處理技術在空間譜估計中有了新的發展。文獻[14-15]采用特殊陣列模型結構，一定程度提高了低快拍數條件下算法的估計性能。文獻[16-17]通過改善信號和噪聲的正交性，來提高算法在低信噪比、小快拍數等復雜環境下的分辨率。然而，當信源角度接近時DOA估計精度將會受到影響。

本文針對低信噪比、小快拍數或信源角度相近等復雜環境下DOA估計性能嚴重下降這一問題，利用MUSIC空間譜函數的二階導數能在原始波達方向周圍產生負峰值的特性，通過對二階導數空間譜進行負峰值搜索實現DOA估計。相比常規DOA估計算法，本文方法在不嚴重增加運算量和計算復雜度的基礎上，大幅度地提高了復雜環境中DOA估計的測向精度，有較強的工程實用價值。

1 信號模型

假設N個窄帶遠場信號源si(t)以角度θi(i=1,2,…,N)入射至空間某均勻線型陣列上，其中陣列天線由M個線性分布陣元組成，假設陣列中各陣元是各向同性的且不存在通道不一致、互耦等因素的影響。假設噪聲為零均值、方差為δ2的高斯白噪聲，陣元間噪聲彼此獨立，且與信號不相關。以最左側陣元為參考陣元，則其陣列接收信號寫成向量表達式為：

X(t)=A(θ)S(t)+N(t)

(1)

式中：X(t)為陣列接收的快拍數據的向量表達式；A(θ)為對應的M×N維陣列流形矩陣；N(t)為噪聲向量。其中:

X(t)=[x1(t),x2(t),…,xM-1(t),xM(t)]T

(2)

A(θ)=[a(θ1),a(θ2),…,a(θM)]

(3)

(4)

S(t)=[s1(t),s2(t),…,sM(t)]T

(5)

N(t)=[n1(t),n2(t),…,nM(t)]T

(6)

R=E[X(t)XH(t)]

(7)

式中：E為期望值；R為信號協方差矩陣。

2 MUSIC算法簡介

對協反差矩陣進行特征分解可得：

(8)

式中：US為大特征值對應的特征向量所組成的信號子空間；Σ為由特征值組成的對角矩陣；UN為小特征值對應的特征向量所組成的噪聲子空間。在理想情況下，數據空間中的信號子空間與噪聲子空間相互正交，即信號子空間中的導向向量也與噪聲子空間正交，則式(9)成立。

aH(θ)UN=0

(9)

(10)

所以，MUSIC算法的譜估計公式為：

(11)

3 改進算法研究

文獻[18]定義當存在某θc滿足θc=1/2(θ1+θ2)且P(θc)=1/2[P(θ1)+P(θ2)]時，兩信號能剛好被分辨出來，此時稱Δ=|θ1-θ2|為MUSIC算法的分辨率。分辨率與采樣快拍數L和陣元數目M均有聯系。Kaveh等[19]定向分析出這幾個變量與角分辨率的關系：

(12)

假設某均勻線陣陣元數為9，2個窄帶遠場信號s1(t)、s2(t)(信源之間相互獨立)入射至該陣列，兩信源的入射角度分別為θ1=0°、θ2=5°，兩信源的信噪比分別為SNR1=4 dB、SNR2=4 dB，空間噪聲為高斯白噪聲。圖1為使用傳統子空間算法進行DOA估計所得空間譜P(θ)。

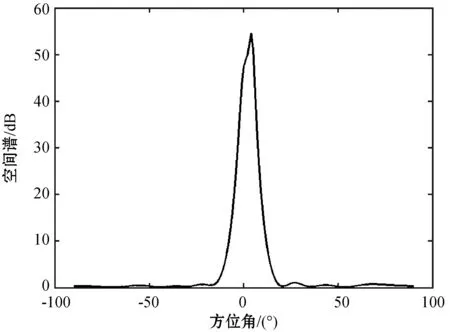
圖1 MUSIC算法空間譜

可以看出，當信源角度接近時，并不會在0°和5°附近分別出現波峰，隨著信源角度間隔減小，兩譜峰將逐漸靠攏，慢慢融合為一，只會在θ=5°附近出現一個峰值，且譜峰不再明顯，我們將不能通過譜峰搜索來確定信號的DOA信息，測向精度降低。

觀察譜峰發現，譜峰附近左側為增函數，即一階導數大于零；右側為減函數，即一階導數小于零。僅依靠函數斜率的正負性的變化里確定極大值點是不夠的，因為在極小值點的附近也會出現一些局部的波動，導致斜率的正負性變動，故函數的極值點一般是通過一階導數和二階導數來確定。對于一元可微函數f(x)，其駐點為x0，且f″(x0)<0，則f(x)在x0處取得極大值。仔細觀察圖1，可以發現在0°和5°之間會出現一段下凹的曲線，考慮對頻譜求二階導數，通過搜索二階導函數的最小值點來確定波達角。

為提高計算精度，可以考慮保留更多的項數，選擇保留二階項，則連續函數二階導數可近似簡化為：

(13)

(14)

一維離散點P(θ)代入式(13)，當1≤i≤L-2時，近似求二階導數值，可得：

(15)

基于譜函數二階導數的DOA估計方法步驟如下：

3) 根據式(11)得到MUSIC算法估計的譜函數P(θ)。

4) 根據式(15)得到譜函數的近似二階導數函數P″(θ)。

5) 對P″(θ)進行負向譜峰搜索，得到極小值點對應的角度即為波達角方向。

4 仿真結果分析

為驗證本文算法的性能，分別將算法與經典DOA估計算法進行比較。為驗證算法的有效性和估計性能，分別進行了三組仿真對比實驗。

實驗一驗證本文算法的估計性能，考慮均勻線陣的陣元數為9，陣元間距為半波長。為實驗方便起見，兩入射信源s1(t)、s2(t)相互獨立，兩信號源的信噪比分別為SNR1=0 dB、SNR2=0 dB，陣列采樣快拍數為200。圖2和圖3是兩信源入射角θ1=0°、θ2=20°時，分別使用傳統MUSIC算法和基于譜函數二階導數DOA估計所得空間譜。圖4和圖5是兩信源入射角θ1=0°、θ2=5°時，分別使用傳統MUSIC算法和基于譜函數二階導數DOA估計所得空間譜。

圖2 θ1=0°、θ2=20°時MUSIC空間譜

圖3 θ1=0°、θ2=20°時二階導數空間譜

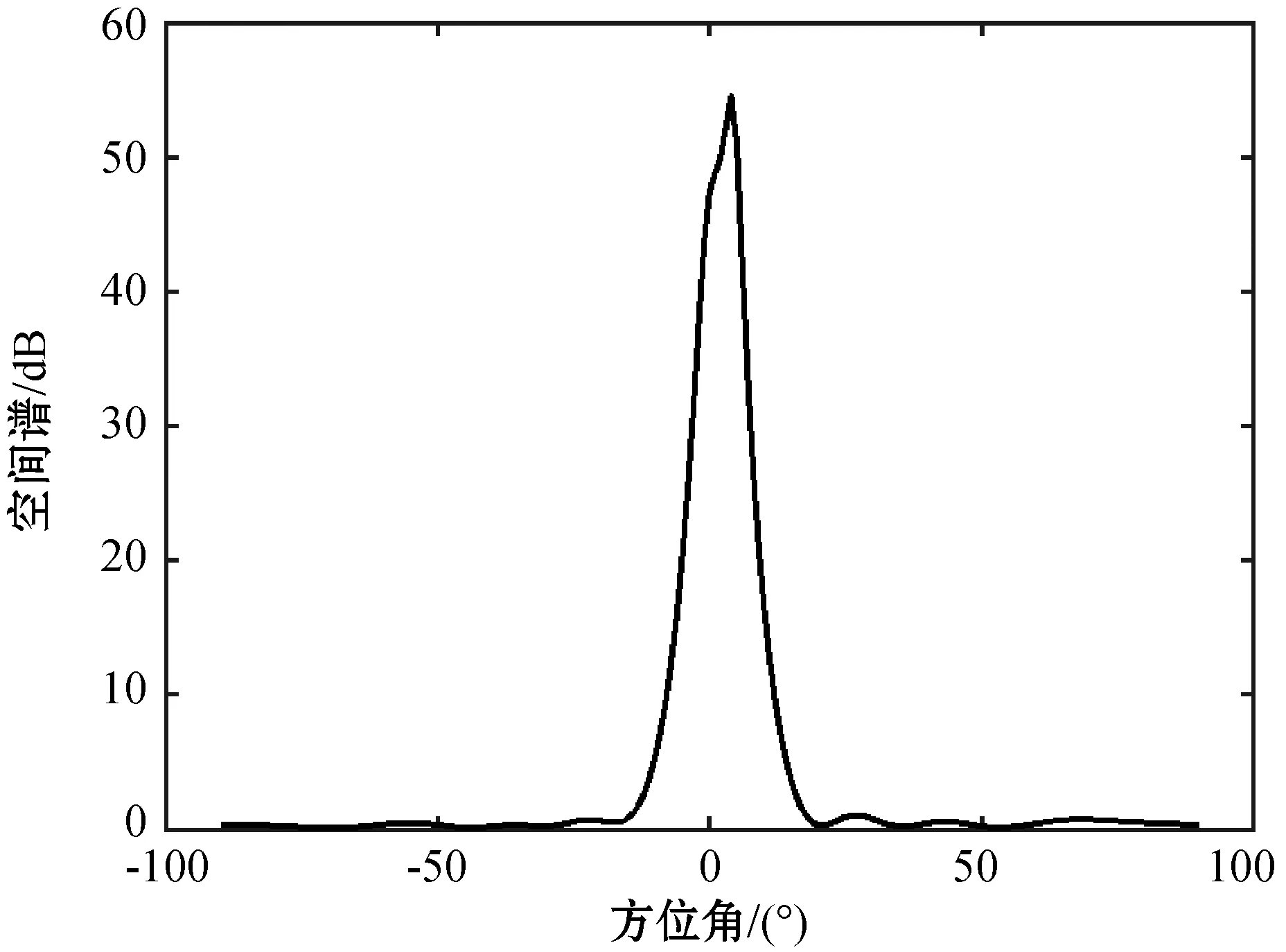
圖4 θ1=0°、θ2=5°時MUSIC空間譜

圖5 θ1=0°、θ2=5°時二階導數空間譜

當信源角度間隔較大時，如圖2和圖3所示，兩種算法所得空間譜均會出現尖銳的譜峰，可以精確估計信源的DOA信息。兩者的不同之處就是：傳統MUSIC算法使用的是正向譜峰搜索，而基于譜函數二階導數的DOA估計是利用大值點附近譜函數的二階導數能在原始波達方向周圍產生負峰值的特性進行負向譜峰搜索。

當信源角度間隔較小時，如圖4所示，傳統MUSIC算法并不能得到兩個尖銳的譜峰，只能在4°附近搜索到一個譜峰，DOA估計性能下降。如圖5所示，即使在信源角度間隔較小時，基于譜函數二階導數的DOA估計算法仍能夠迅速捕捉譜曲線中下凹部分，利用求二階導數形成負向譜峰，進行精確的DOA估計。由此可見：基于譜函數二階導數的DOA估計算法有良好的估計性能。

實驗二驗證本文算法對信噪比的敏感程度。考慮均勻線陣的陣元數為9，陣元間距為半波長，兩入射信源s1(t)、s2(t)相互獨立，兩信源入射角分為θ1=0°、θ2=5°，為避免快拍數對實驗結果的影響，取快拍數為500，信源的信噪比取-2 dB～15 dB，步進為0.5 dB。Monte Carlo實驗次數為1 000。

如圖6所示，隨著信噪比的逐漸提高，兩種算法的均方根誤差均將逐漸減小。本文算法的精確度顯然高于傳統MUSIC算法，即使在信噪比較低的情況下，如SNR=-2 dB，本文算法估計的均方根誤差為0.95，而此時經典MUSIC算法的均方根誤差接近為2；當信噪比達到9.5 dB及以上時，本文算法的均方根誤差為0。

圖6 算法對信噪比的敏感程度

實驗三驗證本文算法對快拍數的敏感程度。考慮均勻線陣的陣元數為9，陣元間距為半波長，兩入射信源s1(t)、s2(t)相互獨立，兩信源入射角分為θ1=0°、θ2=5°，為避免信噪比對實驗結果的影響，取信噪比為8 dB，信源的快拍數取20至800，步進為20。Monte Carlo實驗次數為1 000。

如圖7所示，隨著快拍數的逐漸提高，兩種算法的均方根誤差均將逐漸減小。本文算法的精確度顯然高于傳統MUSIC算法，即使在快拍數較低的情況下，如快拍數為50時，算法估計的均方根誤差為0.55，而此時經典MUSIC算法的均方根誤差接近為1.3，是本文算法的兩倍以上；當快拍數達到650及以上時，本文算法的均方根誤差近似為0。

圖7 算法對快拍數的敏感程度

5 結 語

經典算法受陣列元數、快拍數及信噪比門限的限制，在復雜環境下DOA估計分辨率將嚴重下降。本文利用MUSIC空間譜函數的二階導數能在原始波達方向周圍產生負峰值的特性，研究了基于譜函數二階導數的波達方向估計方法，通過對二階導數空間譜進行負峰值搜索實現DOA估計。仿真實驗表明，相比常規DOA估計算法，本文方法在不嚴重增加運算量和計算復雜度的基礎上，大幅度地提高了復雜環境中的DOA估計的測向精度，有較強的工程實用價值。