基于ISM和GAHP的武器系統選型評價方法

郝坤鵬, 楊國來, 張磊, 葛建立

(1.南京理工大學 機械工程學院, 江蘇 南京 210094; 2.西安昆侖工業(集團)有限責任公司, 陜西 西安 710043)

武器裝備研制是一項龐大、復雜的系統工程，涉及諸多學科領域，包含有分系統和設備，其系統結構、指標體系層次復雜，綜合評估難度大。同時，在武器裝備論證初期，許多指標可能還處于定性描述階段，量化程度低，這就給多方案擇優帶來較大困難。為提高方案擇優的精準性，有必要應用系統工程理論和方法，對武器系統組成要素之間的關系進行分析，構造系統樹狀結構圖，尋找底層基礎要素，對暫時無法量化的指標，利用專家系統，按指標重要性和方案先進性，依據經驗進行定量評價，最終確定武器裝備綜合性能定量評價值，從而找出最優方案，給武器系統論證、選型提供依據。本文提出ISM和GAHP的評價方法，利用ISM構造系統層次結構，利用GAHP進行定量評價，系統地解決了這一問題。

1 基于ISM和GAHP的武器選型評價方法建模

1.1 解釋結構模型ISM

1973年，為了分析更復雜的社會經濟體系問題，美國J·華費爾教授研究了一種新型方法，稱之為解釋結構模型(interpretative structural modeling,ISM)。該方法以人類的實踐經驗和工程理論知識為基礎，充分利用計算機輔助設計軟件，將復雜的系統進行逐層分解，形成由若干個子系統(要素)構成的多級遞推的結構模型，并據此分析各系統構成要素間的相互聯系的程度[1]。已有一些文獻對此方法在多個領域的應用進行了研究[2-5]。

1.2 灰度層次分析法GAHP

灰度層次分析法(grey analytic hierarchy process,GAHP)是一種量化定性指標的方法，用來反映評價指標的層次結構和每個組件之間的內在聯系。運用灰色聚類分析方法，充分挖掘和使用少量的已知信息，盡可能構造完善的數學模型。計算不同聚類指標的白化數，然后對幾個灰度級進行綜合、歸納，確定所屬的聚類，最后得出系統的綜合評價[6]。關于GAHP的應用，已有一些相關研究[7-16]。

1.3 武器選型評價方法建模

基于ISM和GAHP的武器選型評價方法主要適用武器系統方案論證初期，是一種定性與定量相結合的方案評價與選擇的方法。主要思路是：應用ISM思想，采用頭腦風暴與專家評估，確定系統的功能結構與指標層次關系；在此基礎上，應用GAHP思想，通過專家組對比決策，獲得各指標的評價權重，以及各方案的評分，最后獲得各方案的綜合評分，從而選出最優方案。

基于ISM和GAHP的武器系統選型評價方法實現流程如下：

1) 選擇系統要素S

根據系統概念設計和初步方案設想,經專家組分析和討論,確定功能要求和技術途徑,形成系統要素集S。

S={Si|i=1,2,…,n}

(1)

式中:Si為i個系統要素。

2) 建立鄰接矩陣A

鄰接矩陣A(adjacency matrix)表達系統要素之間的相互作用關系,經專家組研討確定。

A=[aij]n×n

(2)

3)建立可達矩陣R

可達矩陣R(reachablity matrix)表達系統要素之間是否可以到達的狀態。

R=[rij]n×n

(3)

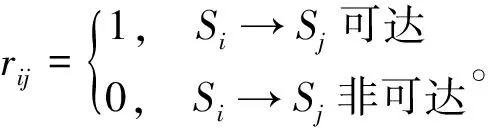
R可以通過A加上單位矩陣I,按照布爾運算法則得到。

定義Ar-1=(A+I)r-1,若存在

A1≠A2≠…≠Ar-1=Ar,r≤n-1,則

R=Ar-1=Ar

(4)

4) 可達矩陣分級

對于要素Si,R中對應于Si的行中，所有要素為1的列所對應的要素Sj構成Si的可達集R(Si);R中對應于Si的列中，所有要素為1的行所對應的要素Sj組成Si的前因集A(Si)。若

R(Si)=R(Si)∩A(Si)

(5)

則Si為本級中最高級要素,組成集合L1。將L1中的要素從系統要素集中刪除,再從余下的要素集中尋找次一級最高要素,直至把所有要素全部完成化級,逐級形成集合L2,L3,…,Lk,則級劃分

ΠL(S)={L1,L2,…,Lk}

(6)

依據ΠL(S)要素順序,對可達矩陣R進行變換,形成新可達矩陣R′

(7)

5) 構建縮減可達矩陣R″

進一步分析可達矩陣R′,若對角子陣Nkk為單位矩陣,表明其無回路;若對角子陣Nkk為滿陣,表明其存在回路,在回路中選擇一個代表要素,去掉其余要素,獲得縮減可達矩陣R″。

6) 構建系統層次結構模型

當所有的子陣處理完畢后,即可獲得武器系統層次結構模型,底層元素為武器系統的評估指標集合C

C={ci|i=1,2,…,m}

(8)

式中:ci為第i個評估指標。

7) 確定指標的權系數向量Λ[17]

專家組對待評估目標m變量按其相對重要性兩兩相互比較打分,構建判斷矩陣B

B=[bij]m×m

(9)

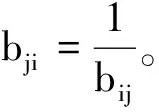
根據判斷矩陣B,求解權系數向量Λ

Λ=[λ1,λ2,…,λm]T

(10)

式中

獲得權系數向量Λ后,需進行一致性判斷。其中λmax表示判斷矩陣的最大特征值,CR表示一致性指標。分別對其進行計算

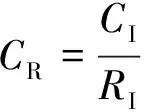
(11)

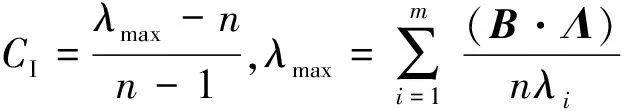
RI為平穩隨機一致性指標[18]。

若CR遠遠小于0.1,則認為其一致性符合需求,此矩陣具有較好的一致性,得到的權系數值滿足要求,否則,需對B進行必要調整。

8) 計算指標評估值矩陣D

獲得指標權系數向量Λ后,對待評的p個方案,組織q名專家組按指標集C中各指標要素逐一對待評方案先進性進行打分,最低0分,最高9分,獲得指標評估矩陣D

(12)

9) 確定評估灰度f

某受評指標c的評估灰度f主要包含灰度等級數、灰度的灰數、灰度的白化權函數。常用的白化權函數有下述3種[19-20]。

(1) 第一級“高”(e=1),灰數1?∈[d1,∞],白化函數為:

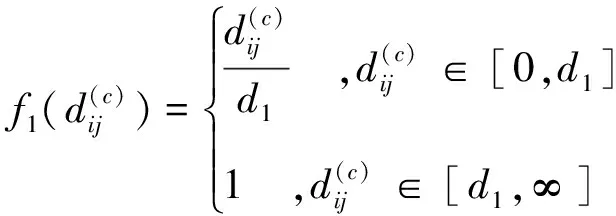
(13)

(2) 第二級“中”(e=2),灰數2?∈[0,2d2],白化函數為

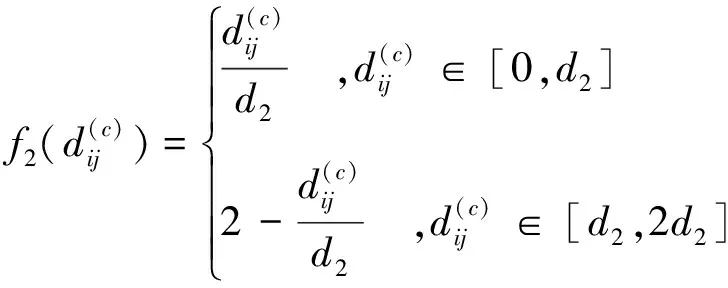
(14)

(3) 第三級“低”(e=3),灰數3?∈[0,d4],白化函數為

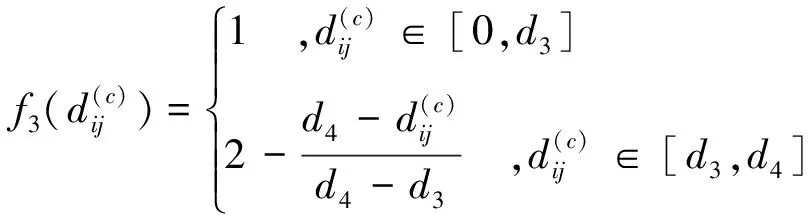
(15)

10) 計算灰度矩陣X及灰度系數矩陣T

對某受評指標,應用e個灰度白化函數f,以及指標評估矩陣D,計算其灰色矩陣X(c)

X(c)=[xij]p×e

(16)

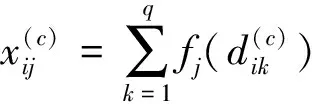
指標ci的灰度評估系數矩陣T(c)

T(c)=[tij]p×e

(17)

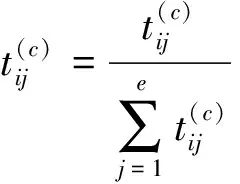
11) 計算灰色評估矩陣U

依據指標灰度評估系數矩陣T(c),按照最大化原則,可以獲得m個指標的p個方案的灰色評估矩陣U

U=[uij]p×m

(18)

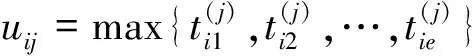
12) 計算綜合評價值W

綜合評價值W

W=UΛ

(19)

2 某機載武器系統選型評價應用示例

1) 選擇系統要素

根據某機載武器系統論證需求,成立一個有行業研究經驗的論證小組,根據機載武器系統作戰需求以及當前技術發展現狀,采用頭腦風暴等方法,立足作戰使用、裝備保障、研制可行性等裝備全壽命周期的能力需求,提出了24個決策要素,構建了機載武器系統要素集S,見表1。

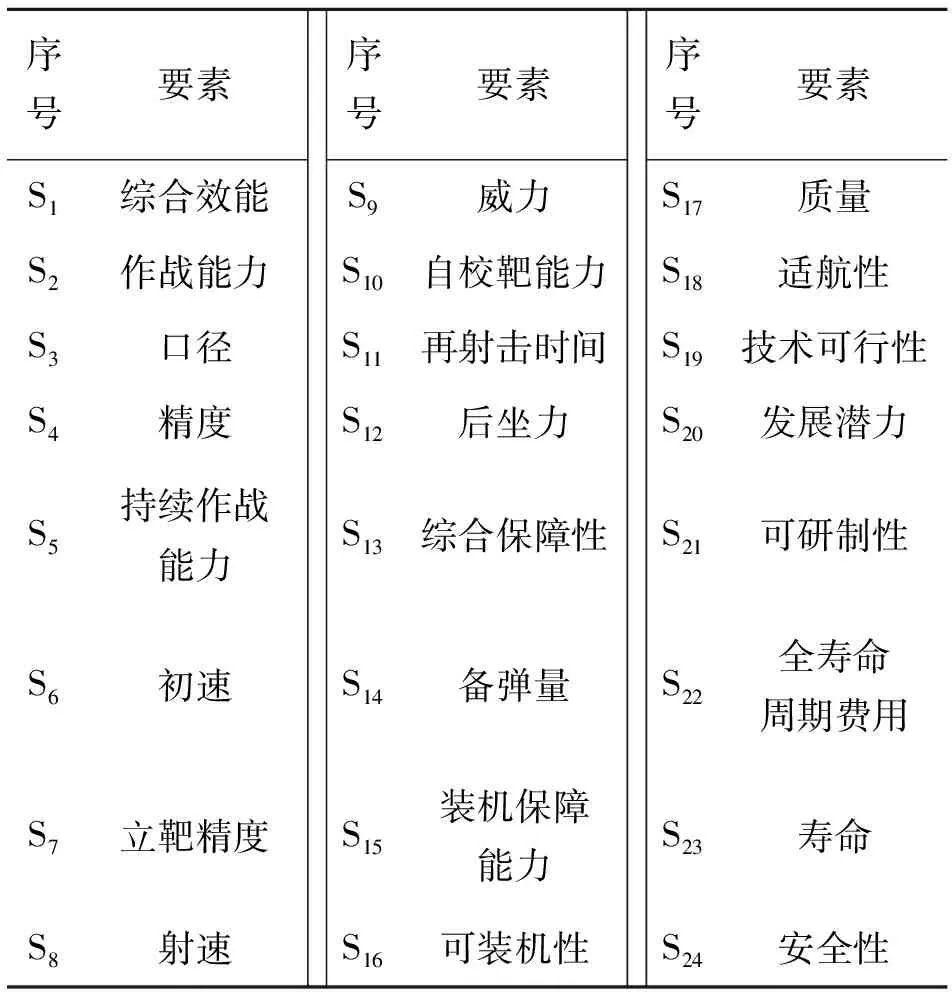
表1 某機載武器系統要素集

2) 建立鄰接矩陣

專家組結合其他同類產品要素作用關系,逐一分析,確定了各要素的作用關系,如S2與S1有關,a21=1,與其他要素無關,a2j=0;建立鄰接矩陣A如下

3)建立可達矩陣R

按(4)式進行布爾運算,獲得可達矩陣R

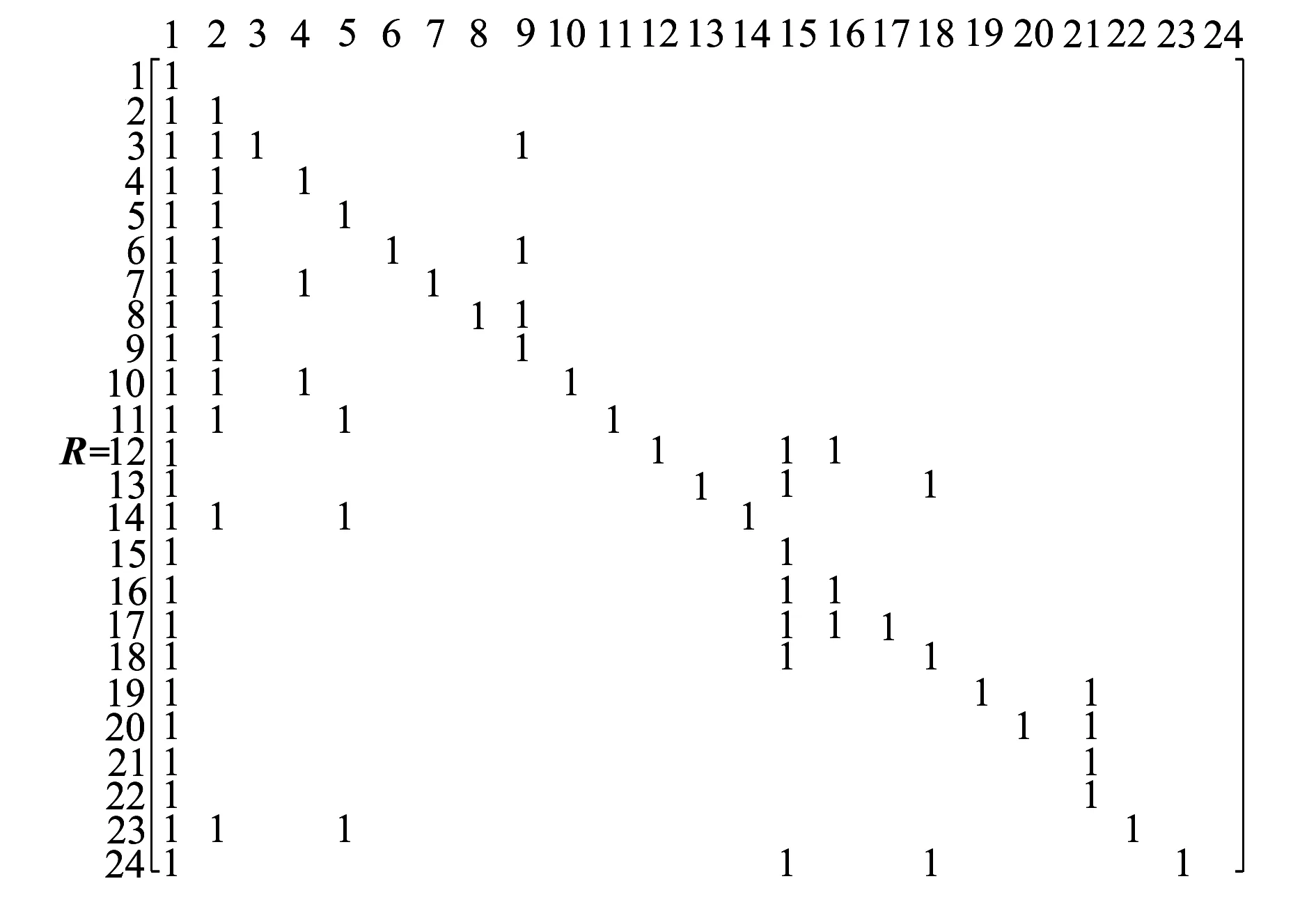
4)可達矩陣分級

計算各要素的R(Si)、A(Si)以及R(Si)∩A(Si),詳見表2。

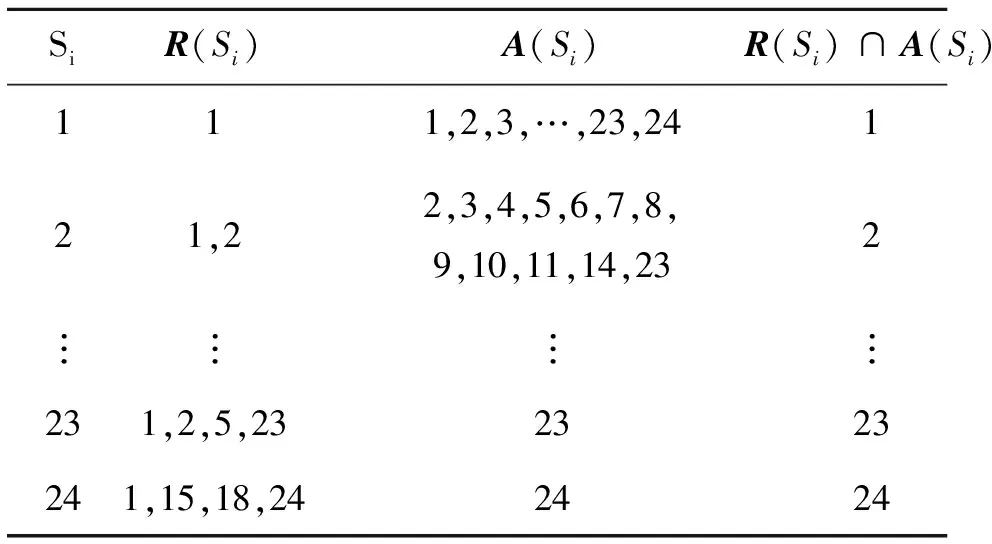
表2 某機載武器系統可達集、前因集

按(6)式判斷要素層級,依次得到

依據ΠL(S)要素順序,對可達矩陣R進行變換,形成新可達矩陣R′

5) 構建縮減可達矩陣R″

對可達矩陣R′進行分析,其不存在回路,則縮減可達矩陣R″=R′。

6) 建立結構模型

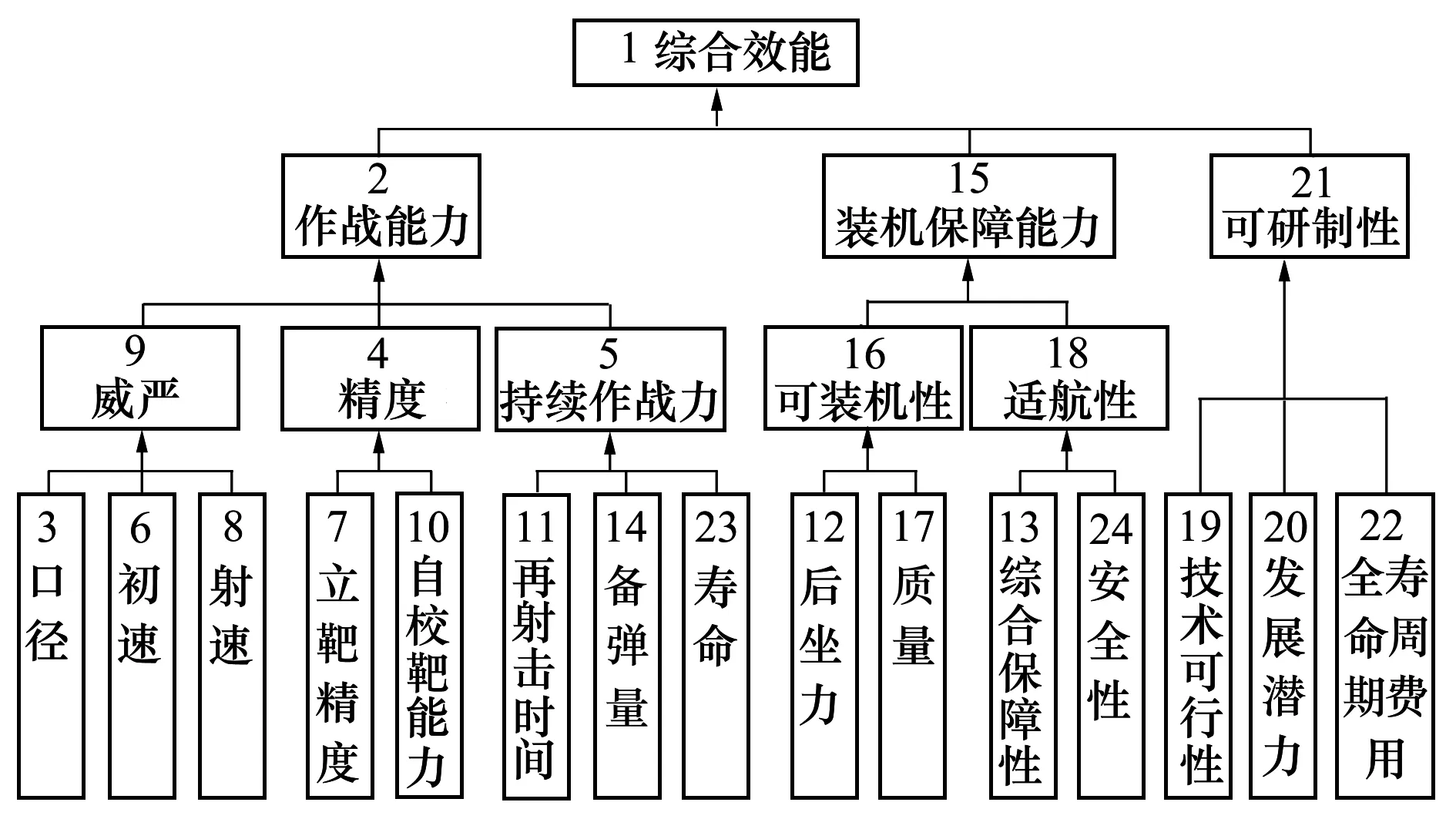
圖1 機載武器系統結構模型

從圖1可知,通過解釋結構模型的計算、排序,某機載武器系統要素構成了一個4層結構模型。

第1層為綜合評價層,由系統要素“綜合效能(S1)”構成。綜合評價層一般作為決策機關關注重點,用于項目決策及選型。

第2層為能力評價層,表征了全壽命周期的核心能力,由系統要素“作戰能力(S2)、裝機保障能力(S15)和可研制性(S21)”構成。能力評價層一般作為項目管理機關關注重點,用于項目方案的綜合評價及全壽命管控。

第3層為性能評價層,表征了裝備戰術性能,由系統要素“威力(S9)、精度(S4)、持續作戰能力(S5)、可裝機性(S16)和適航性(S18)”構成。性能評價層一般作為型號研制總師關注重點,用于裝備研制關鍵參數控制。

第4層為技術評價層,表征了裝備戰術指標,由系統要素“口徑(S3)、初速(S6)、射速(S8)、立靶精度(S7)、自校靶能力(S10)、再射擊時間(S11)、備彈量(S14)、壽命(S23)、后坐力(S12)、質量(S17)、綜合保障性(S13)、安全性(S24)、技術可行性(S19)、發展潛力(S20)和全壽命周期費用(S22)”構成。技術評價層一般作為裝備設計與驗收人員關注重點,用于研制過程的技術實現及風險管控。

7) 計算評價指標的權重

對于第一層次“綜合效能”的“作戰能力、裝機保障能力、可研制性”3個要素,組織專家組建立判斷矩陣B1

按(10)式計算權Λ1

Λ1=[0.588 9,0.251 9,0.159 3]T

按(11)式計算判斷矩陣的最大特征值λmax和一致性指標CR

λmax=3.053 9,CI=0.0270,CR=0.051 8

CR≤0.1,矩陣的一致性滿足要求,權系數值可行。

同理計算第二、第三層指標構成要素的權系數,不同之處在于,所得權系數上乘以上一級的權系數,最終獲得對第一層的權系數。

Λ21=[0.252 4,0.252 4,0.084 1]T

Λ22=[0.167 9,0.084 0]T

Λ23=[0.115 2,0.030 8,0.013 3]T

Λ311=[0.018 6,0.071 4,0.162 4]T

Λ312=[0.220 8,0.031 5]T

Λ313=[0.007 4,0.020 5,0.056 3]T

Λ321=[0.146 9,0.021 0]T

Λ322=[0.056 0,0.028 0]T

根據層次分析,選擇底層要素3,6,8,7,10,11,14,23,12,17,13,24,19,20,22共15個要素進行綜合評價,其權系數Λ為

利用權系數Λ繪制指標-權重圖,見圖2。

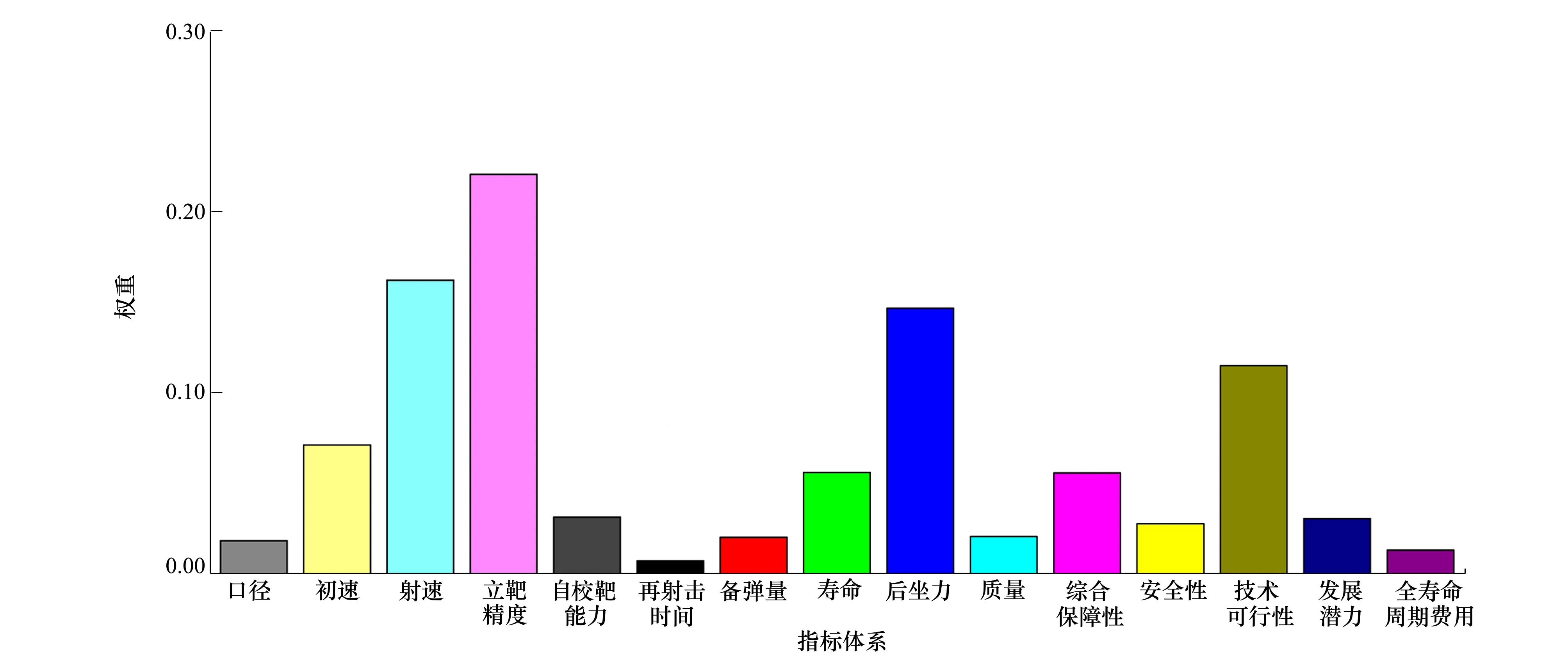
圖2 機載武器系統指標-權重

從圖2可知,初速(S6,0.071 4)、射速(S8,0.162 4)、立靶精度(S7,0.220 8)3個指標權重較高,對作戰能力的貢獻主要體現在單位時間內快速(射速)、精準(立靶精度)發射高威力彈藥(初速)技術上;后坐力(S12,0.146 9)權重較高,對裝機保障能力的貢獻主要體現在降低后坐力對載機的沖擊、振動載荷,提高載機與武器的兼容性上;技術可行性(S19,0.115 2)權重較高,對可研制性貢獻體現在裝備可實現性上,這幾個指標應當被武器裝備研制者高度關注,并不斷迭代提升。

8) 計算指標評估矩陣D

組織專家組按指標S逐一對待評方案先進性進行打分獲得指標評估矩陣D，其中

以及D(6),D(8),D(7),D(10),D(11),D(14),D(23),D(12),D(17),D(13),D(24),D(19),D(20),D(22)。

9) 確定評估灰度f

根據系統特點,選擇4級灰度(“中”選擇2級),第一級“高”(e=1),d1=9,灰數1?∈[9,∞];第二級“中”(e=2),d2=8,灰數2?∈[0,16];第三級“中”(e=3),d3=6,灰數3?∈[0,12];第四級“差”(e=4),d4=1,d5=5灰數4?∈[0,5]。

10) 計算灰度矩陣X及灰度系數矩陣T

對受評指標“口徑”,應用灰度白化函數f,以及評估指標矩陣D(3),按(16)～(17)式計算其灰色矩陣X(3)、灰度評估系數矩陣T(3)

同理,可計算其他指標灰度矩陣X及灰度系數矩陣T。

11) 計算灰色評估矩陣U

依據指標灰度評估系數矩陣T(A),按(18)式計算灰色評估矩陣U為

利用灰色評估矩陣U繪制指標-灰度評估值圖,見圖3。

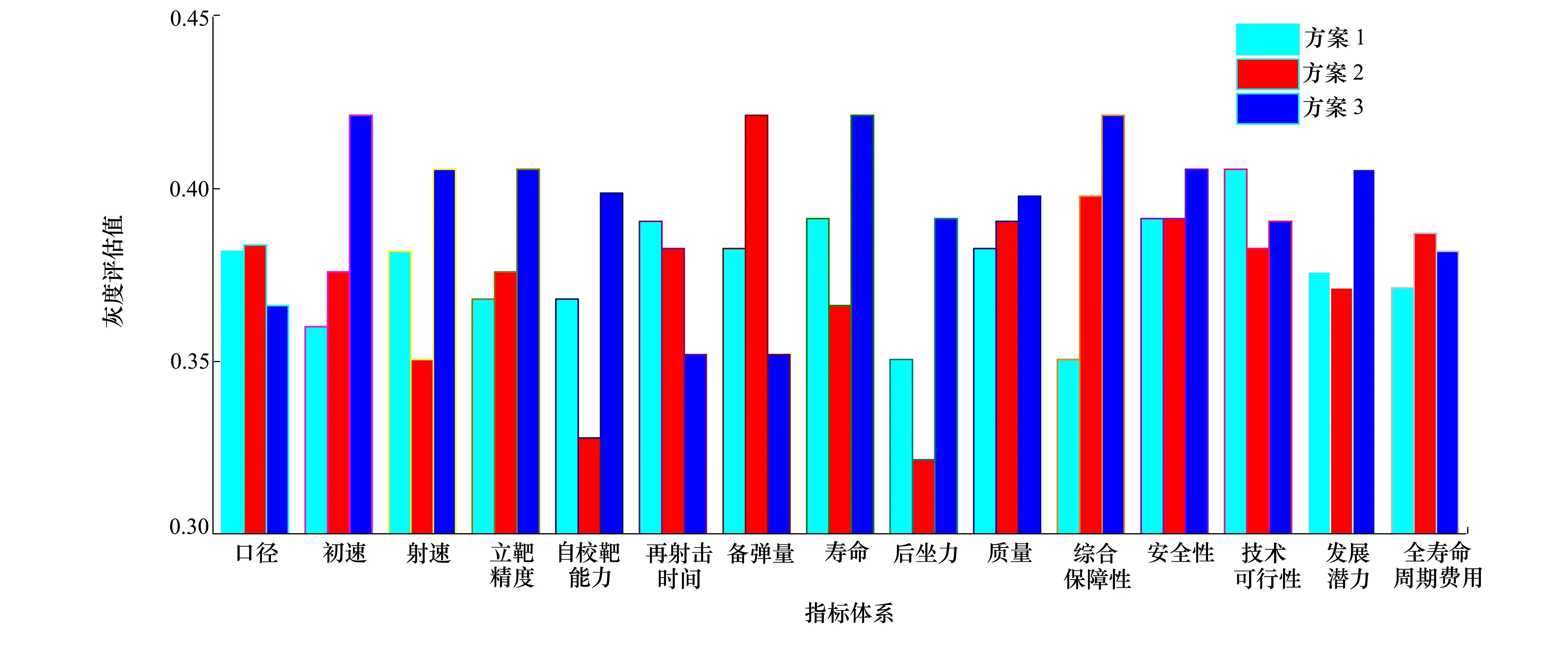
圖3 機載武器系統指標-灰度評估值

12) 綜合評價值W

按(19)式計算綜合評價值W

結果可知,方案3比方案1、方案2更加優異。

從圖3可知,在不計及指標權重的情況下,方案3初速(S6)、射速(S8)、立靶精度(S7)、后坐力(S12)等核心指標的灰度評估值明顯優于方案1和方案2,抓住了武器研制的核心指標;同時自校靶能力(S10)、壽命(S23)、重量(S17)、綜合保障性(S13)、安全性(S24)以及發展潛力(S20)也優方案1和方案2,其對指標的平衡性也是予以重點關注。從綜合評價值看,計及指標權重的情況下,方案3之所以獲勝,一是緊緊把握了關系武器系統成敗的關鍵指標予以突破；二是同步全面、均衡發展其他技術指標,確保綜合性能不僅局部最優,而且全域最優的設計思想。

3 結 論

基于ISM和GAHP的武器系統選型評價方法解決了武器裝備論證初期系統方案擇優的問題，可提高武器裝備論證的水平。特點如下：

1) 利用ISM方法，將復雜系統的多要素的關系進行結構化、層次化梳理，層次結構圖表征了參量之間的相互影響關系，揭示了構成武器系統的最底層要素；

2) 利用GAHP方法，定量描述了影響上一級要素，以及最上一級要素的要素之間的重要程度，給裝備研制全壽命周期過程控制、資源投入、性能驗證等工作指明了方向；

3) ISM和GAHP方法將定性描述轉化為定量描述過程中，引入多人專家組的打分系統，并對偏離中心的差異性得分進行了加權處理，避免了專家個人的主觀偏離對評價結果公正性的影響。