線性樹模型的Sporadic任務多核調度方法研究
黃姝娟, 李天森, 馬志昊, 肖鋒
(西安工業大學 計算機科學與工程學院, 陜西 西安 710021)
片上多核處理器任務調度方法中,研究者早期考慮的是基于由Liu 和Layland[1]提出的相互獨立的實時周期任務模型[2-10],隨著研究的深入,又開始研究執行時間可以隨著關鍵級別變化而變化的混合關鍵任務模型[11-13]和具有制約關系以及帶有周期性的DAG任務模型[14-19]。這些模型對應的調度算法大都是基于RM(rate-monotonous)算法和GEDF(global earliest deadline first)以及PEDF(partitioned earliest deadline first)算法。如文獻[2,4-5]和文獻[3,6-7]針對相互獨立的實時周期任務,分別對RM算法及GEDF算法進行分析并提出新的調度算法。文獻[8]針對PEDF中的劃分算法,提出一種改進的基于冪函數劃分的EDF算法。文獻[9-10]則是結合PEDF和GEDF各自優點,提出了旨在允許部分任務遷移的semi-partitioned調度算法。文獻[11]將PEDF改進的semi-partitioned算法應用在混合關鍵模型中。文獻[13]則是將周期性的DAG圖放在混合關鍵模型中討論。文獻[14-16]在GEDF算法下討論DAG圖的調度。文獻[17]則提出一種PEDF-omp的調度算法,旨在解決類似DAG圖模型的OpenMP并行執行。文獻[18]在big.LITTLE體系結構下研究不同類型周期任務的動態分區調度方法。文獻[19]則針對既考慮周期性又考慮依賴關系的實時周期性任務,提出基于可延遲時間越短越優先(PLTSF,probably lag time shortest first)的調度方法。
上述所有任務模型中都有一個前提假設,就是所有周期任務均為固定周期。而在實際情況中,有些任務的周期是可以進行調整的。因此本文則針對周期可變的Sporadic任務,提出相應的task模型、job模型以及fragment模型,將實時周期任務劃分為不同層數節點,根據每個節點的實時性、周期性以及節點之間的層次關系進行相應的線性樹模型轉化,并根據具有時間遷移特性的job以及可變周期的任務調整某些層節點的位置,使得盡可能多的節點成為處理器上能夠滿足時限的執行節點。實驗表明,上述調度方法與PEDF、GEDF、RMFF(RM first fit)算法比較起來,在延遲時間、系統利用率、上下文切換次數、系統搶占次數、時限丟失率方面都較優。
1 實時可變周期任務模型
1.1 task模型
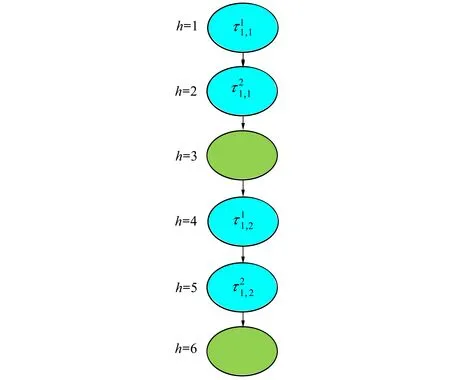
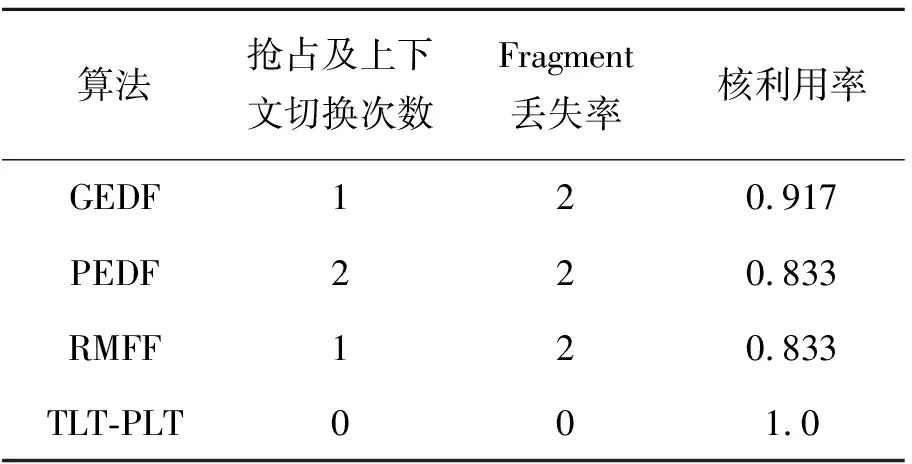
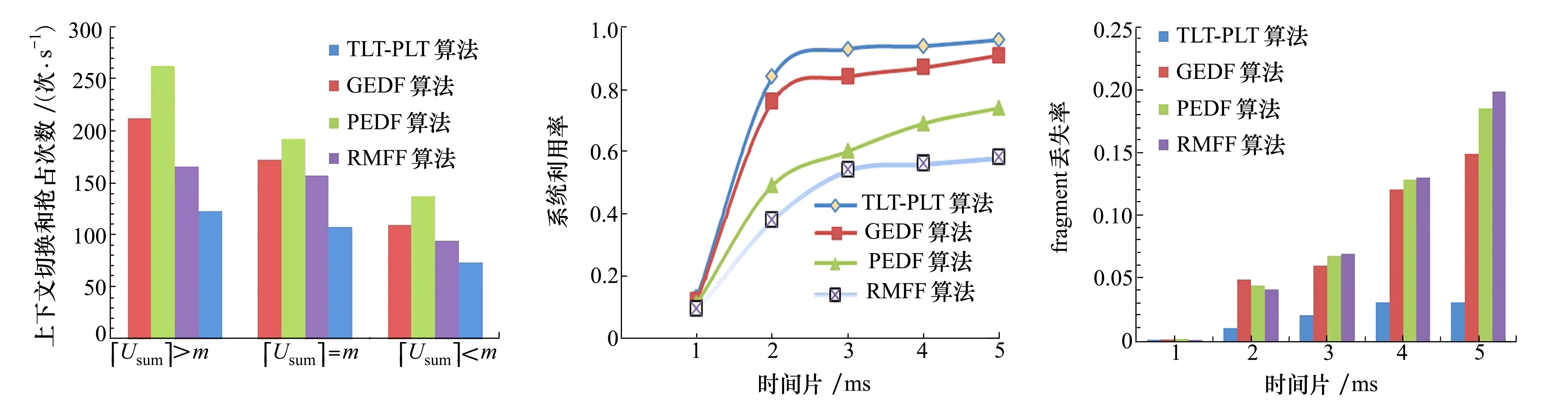
假設一個實時系統τ由n個實時周期性任務組成,記為τ={τ1,τ2,…τn}。每個實時周期任務都包含5個參數,即τi(ri,ei,pi,di,fi)(1≤i≤n)。其中ri表示發布時刻(release time),即處理器核可以執行該任務的時刻。ei表示任務τi最壞情況下的執行時間(worst-case execution time,WCET)。pi是τi的最長周期;di表示時限(deadline),要求ei≤di≤pi。如果di=pi,稱該系統為隱含時限的系統(implicit deadline system),將其任務稱為隱含時限任務。如果di 在一個實時周期任務系統中,所有任務在同一個時刻發布它們的第一個job,將其稱為同步系統,否則稱為異步系統。τi的第j(j≥1)次執行稱為第j個job,用τi,j(ri,j,ei,j,di,j,si,j)表示,其中ri,j為τi,j的最早可以開始執行的時間且ri,j=ri+(j-1)pi-si,j,di,j為τi,j的絕對時限且di,j=ri+(j-1)pi+di,如果di=pi則di,j=ri+j×pi;ei,j為τi,j的執行時間且ei,j=ei。si,j=fi(j)表示τi,j允許提前發布的時間片數量,如果si,j=0,則表示不可以提前發布。 根據樹定義Tree=(root,R),root為根節點,R為樹中各節點之間的層次關系,由樹的特性可以知道樹中的每個節點都有層次,根為第一層,根的孩子為第二層。若某個節點在第h層其孩子就在第h+1層,樹的深度為樹中節點的最大層次。樹T深度為H用layer(T)=H表示;節點Pi所處的層次為h用layer(Pi)=h來表示。 假定一棵樹型結構,除了葉子節點外,所有父節點都只有一個孩子節點,這種樹稱為線性樹LT(line tree)。 LT具有如下特征: 1) 樹中第h層的節點數用Number(h)來表示。顯然Number(h)=1。 2) 由于每層只有一個節點,則該線性樹上所有節點的個數等于該線性樹的層數。 3) 節點之間具有一定的時間順序關系。 線性樹滿足樹的基本特征即在任意一棵樹中: 1) 有且僅有一個特定的稱為根的節點; 2) 當n>1時,其余節點可分為n個互不相交的有限集合T1,T2,…,Tn,其中每一個集合本身又是一棵樹,并且稱為根的子樹。 定義1PLT(processor line tree)模型是由處理器核數M和所有任務周期的最小公倍數D決定的M棵線性樹組成的森林,記為F=(M,D)。其中M為線性樹的個數,D為其中任何一個線性樹的深度,可以看出這M個線性樹的深度都是D。 定義2TLT(task line tree)模型是由任務數量N和任務周期最小公倍數D決定的N棵線性樹組成的森林,記為F=(N,D)。其中N為線性樹的個數,D為其中任何一個線性樹的深度,可以看出這N個線性樹的深度都是D。 圖1 τ1(2,3,f1)在[0,6)時間段的TLT模型 可以看出,如果第一個job的τ1,1允許周期縮短,則縮短的時間片f1(1)≤3-2=1,即τ1,1與τ1,2之間的空節點層數。另外,空節點層以上的節點也可以下移至空節點層處,不影響該節點按時完成。 同樣,PLT模型中線性樹的節點也是處理器核上準備執行任務job的時間片段fragments,由于與TLT模型線性樹的數量不同,通常情況下,M 將2個公式聯立起來得 得證。 推論1任何一個時刻t都能唯一對應于TLT模型的某一層。 證明根據推論1,在TLT模型中,任何時刻都可以對應其中一個層,那么某個h層也可以對應其中某一個fragment的發布時刻,但由于該fragment所在的job提前發布至h′層,則該h層如果不為空節點層必然存在 h≤h′+ei-1 (3) 式中,k=1,根據定理及公式(3) 考慮一個任務系統Γ={τ1,τ2,…,τN}有N個任務要分配到M個處理器上,該系統具有TLT模型和PLT模型分別簡單記為TLTΓ={TLT1,TLT2,…,TLTN}和PLTΓ={PLT1,PLT2,…,PLTM}。所有任務的job被劃分為不同的fragment分布在TLTΓ的不同節點上,然后根據一定的指派算法被指派在PLTΓ這M棵PLT樹節點上。其中所有PLTp(1≤p≤M)均為一棵深度為D的樹,這里D為所有任務周期的最小公倍數,D=[p1,p2,…,pn](D>1),PLTΓ中的一棵PLT樹就對應一個處理器核調度的一個順序。 圖2 實例對應的TLT模型 以該實例來說明TLT模型與PLT模型之間的轉化方法,如圖3所示。 圖3 實例中TLT模型與PLT模型之間的轉化方法 得到PLT的結果如圖4所示。 圖4 轉化為PLT的最終結果 (x=1,…,k),如果系統在允許范圍內,則該節點為可提前發布時間節點。 定義4在指派算法S下,定義一個層次分配函數為hs(x),該函數表示fragmentsx被指派在哪個層,定義Is(x)表示指派在哪棵線性樹上。如果沒有被指派則這兩個函數值均為0。 在指派算法S下,如果一個任務Ti在公共周期內發布的所有τi,j的所有fragments都被指派到LT樹上,且都時限滿足,那么該任務在S下可調度,如果系統內所有任務都可調度,那么該系統在S下可調度。 本文根據PLT空節點層和TLT需要遷移的節點層的情況實現TLT向PLT的轉化算法。 算法:TLT-PLT轉化算法 Input: Enter TLT Set N: The number of tasks M: The number of processors Output: Header Pointer of PLT 1:i=1; 2: Whilei≤Mdo /*Select minimum quantity empty layer number of LT from TLT into PLT*/ 3:j=findMiniEmptyLayer(TLT); 4: Trans(j,TLT,PLT); 5:Delete(j,TLT);/*Delete the LT from TLT set*/ 6:i=i+1; 7: end While /*count the node layer number before every empty layer for every LT in TLT */ 8: Count(TLT, nodeLayerTLT); 9: Count-emptyLayer(PLT, emptyLayerPLT);/ *count the empty layer for every LT in PLT*/ 10: While TLT set is not NULL do /*Select the maximum number of the nodeLayerTLT equal or smaller than the number of emptyLayerPLT */ 11: flag=FindSame(nodeLayerTLT, emptyLayerPLT) 12: if(flag!=-1 && Layer is equal) /*move the node layer of LT in TLT into the empty layer of PLT*/ 13: Trans(flag, nodeLayerTLT, emptyLayerPLT, TLT, PLT); /*move the node layer of LT in PLT to the same empty Layer */ 14: else if (flag!=-1&&Layer is not equal) 15: Move(emptyLayerPLT, PLT); 16: Trans(flag, nodeLayerTLT, emptyLayerPLT, TLT, PLT) 17: else if(advancedPermitted(flag, function)) 18: Advance(flag, TLT);/*count the advanced function if the node is permitted advanced */ 19: else 20: FragmentMiss (flag, TLT);/*put the LT node into the fragment miss set*/ 21: end if 22: Delete(flag, TLT); 23: end While 上述算法核心思想如下: 首先,從TLT中找出M個空節點層數較少的LT轉移到PLT中,并從TLT中刪除這些節點。 其次,計算TLT中每個LT的空節點層數之前的連續節點數,計算PLT中連續空節點層數的數量。 最后,從大到小在TLT中找出連續節點層數與PLT中連續空節點數層數相同的PLT樹,如果匹配則直接將這些節點與對應的PLT中的空節點層進行交換,并刪除TLT中交換過的節點;如果沒有匹配的則將PLT中的節點進行層數下移至數量相同的空節點層,再進行交換并刪除TLT中交換過的節點;如果找不到對應的層數,或者TLT中無法再通過下移空節點層來匹配TLT中的節點層則將剩余節點放置到fragment丟失集合中。 下面就是利用TLT-PLT轉化算法的整體方案。 2.2節的實例在GEDF、PEDF、RMFF以及TLT-PLT 4種調度算法的處理器分配結果如表1~4所示,在6個時間片內的性能統計如表5所示。 表1 實例在GEDF調度算法下的運行結果 表2 實例在PEDF調度算法下的運行結果 表3 實例在RMFFF調度算法下的運行結果 表4 實例在TLT-PLT調度算法下的運行結果 表5 實例在6個時間片內4種算法下的性能比較 本文的仿真實驗平臺是在4核 Intel core(TM)2 Quad CPU 2.66 GHz內存為3.4G的硬件環境下運行Ubuntu Linux10.04 2.6.33-29實時內核,采用Codeblocks-v10.05 編寫仿真測試程序。在實驗設計時,選擇了處理器核數M與N個任務總利用率之間3種不同的關系:「Usum?>m,「Usum?=m,「Usum? 上下文切換和搶占次數。通過計算不同任務job之間上下文切換次數以及job的fragment被打斷情況的計數來統計搶占次數,說明不同算法的額外開銷。開銷太大則耗時多,任務響應時間長。 核利用率。 在算法分配過程中如果PLT模型中線性樹有空節點層,則說明核在該層處于空閑狀態,為了描述核利用情況定義核利用率為該核對應的線性樹的非空節點個數與樹深度的比值。該比值是PLT模型對核利用情況的一個反映。該值越大說明該模型和調度方法對核的利用越充分。 Fragment丟失率。由于PLT模型中的工作在調度過程中存在時限不滿足情況,為了考察時限不滿足嚴重程度定義fragment丟失率為fragment丟失時限節點的數量總和與所有fragments數量總和的比值。 根據以上的評價指標,對可并行執行的工作分別采用GEDF算法、PEDF算法、RMFF算法以及TLT-PLT 轉化算法進行調度,在500個時間片內對系統的上下文切換次數以及搶占次數、核利用率以及fragment丟失率進行了統計。 圖5展示了在3種情況下,每種情況隨機輸入10組數據得出的上下文切換次數和搶占次數的平均值。從圖5中可以看出在負載量較大情況下,TLT-PLT算法的上下文切換及搶占次數明顯小于GEDF、PEDF和RMFF算法,而在負載量小的情況下對比不是很明顯,因此本文僅針對負載量較大的情況,3種算法的核總利用率和fragment丟失率的情況分別如圖6和圖7所示。 核利用率效果如圖6所示。結果顯示出采用TLT-PLT算法的核利用率效果和GEDF基本接近且速度快,而比PEDF和RMFF要好得多。原因是GEDF是允許任務遷移且由最近時限來決定優先級,效率高遷移開銷大;而PEDF是不允許任務遷移利用率較低;RMFF通過利用率進行首次適應匹配,也不允許遷移,利用率也比較低。而TLT-PLT算法結合三者的優點,即允許部分任務遷移又利用LT的空閑節點進行節點空閑節點自適應匹配,且通過調整發布時間可以快速使得任務被調度,因此效率較高。 從圖7中可以看出任務的fragment丟失率隨著時間的持續而增長,但TLT-PLT增長的趨勢較低。分析原因發現由于GEDF算法和RMFF以及PEDF算法優先級是根據自身的參數(時限和利用率)來決定的,并沒有綜合考慮任務的實際執行情況,GEDF由于遷移頻繁而導致有些任務來不及執行就放棄了,PEDF和RMFF算法不能根據時間靈活遷移導致很多任務無法及時執行。而TLT-PLT算法從一開始就利用最小公倍數分時間段考慮任務在實際執行過程中出現的遷移情況以及fragment是否能滿足的問題,并通過調整發布時間使得fragment盡量減少丟失,所以得到最好的效果。 圖5 3種情況下上下文切換 圖6 4種算法核利用 圖7 固定時間片下4種算法 和搶占次數測試 率增長情況 的fragment丟失率 隨著多核技術在嵌入式領域的快速發展,圍繞片上多處理器實時調度問題進行了大量的研究工作,所提出的調度模型和調度算法大都只針對任務模型。本文從線性樹模型出發,根據Sporadic任務周期可變的情況,建立實時周期任務的task模型、job模型以及fragment模型,提出實時周期任務在多核處理器上的TLT模型和PLT模型和相應的轉化算法,不僅維持了系統利用率和減少時限丟失情況,而且還使得切換次數和搶占次數降到比較低的水平。文章首先描述了TLT任務模型和PLT模型,接著說明了該模型的相關性質和相關定理,隨后定義了延遲因子以及相應的轉化算法。仿真實驗表明所采用的TLT-PLT轉化算法不但比PEDF、GEDF、RMFF算法在核利用率以及時限丟失率方面都較優而且還減少了搶占次數和上下文切換次數。1.2 job模型
1.3 fragment模型
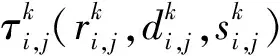
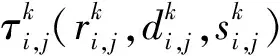
2 TLT和PLT模型
2.1 相關定義
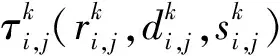
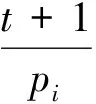
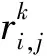
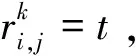
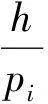
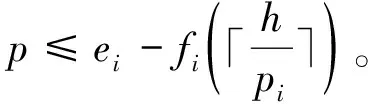
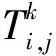
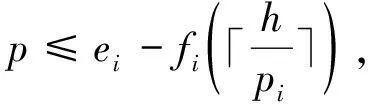
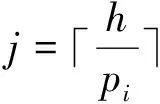
2.2 實時系統的TLT模型和PLT模型
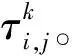
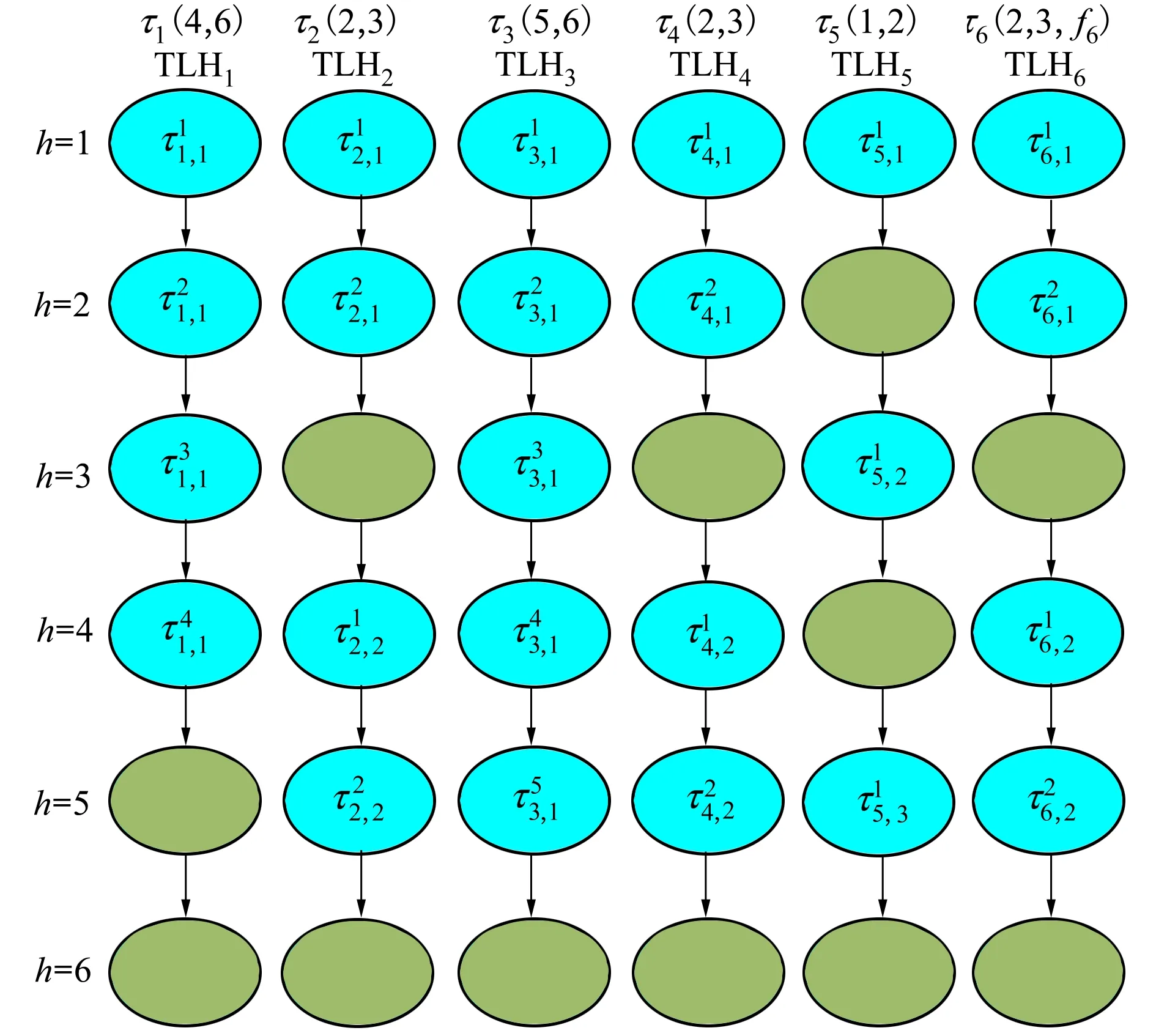
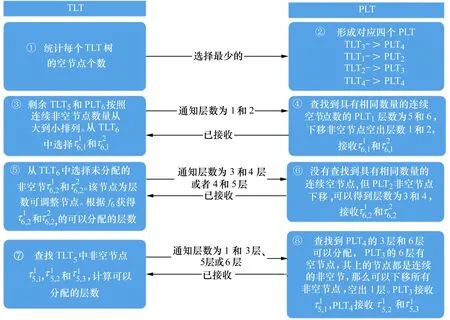
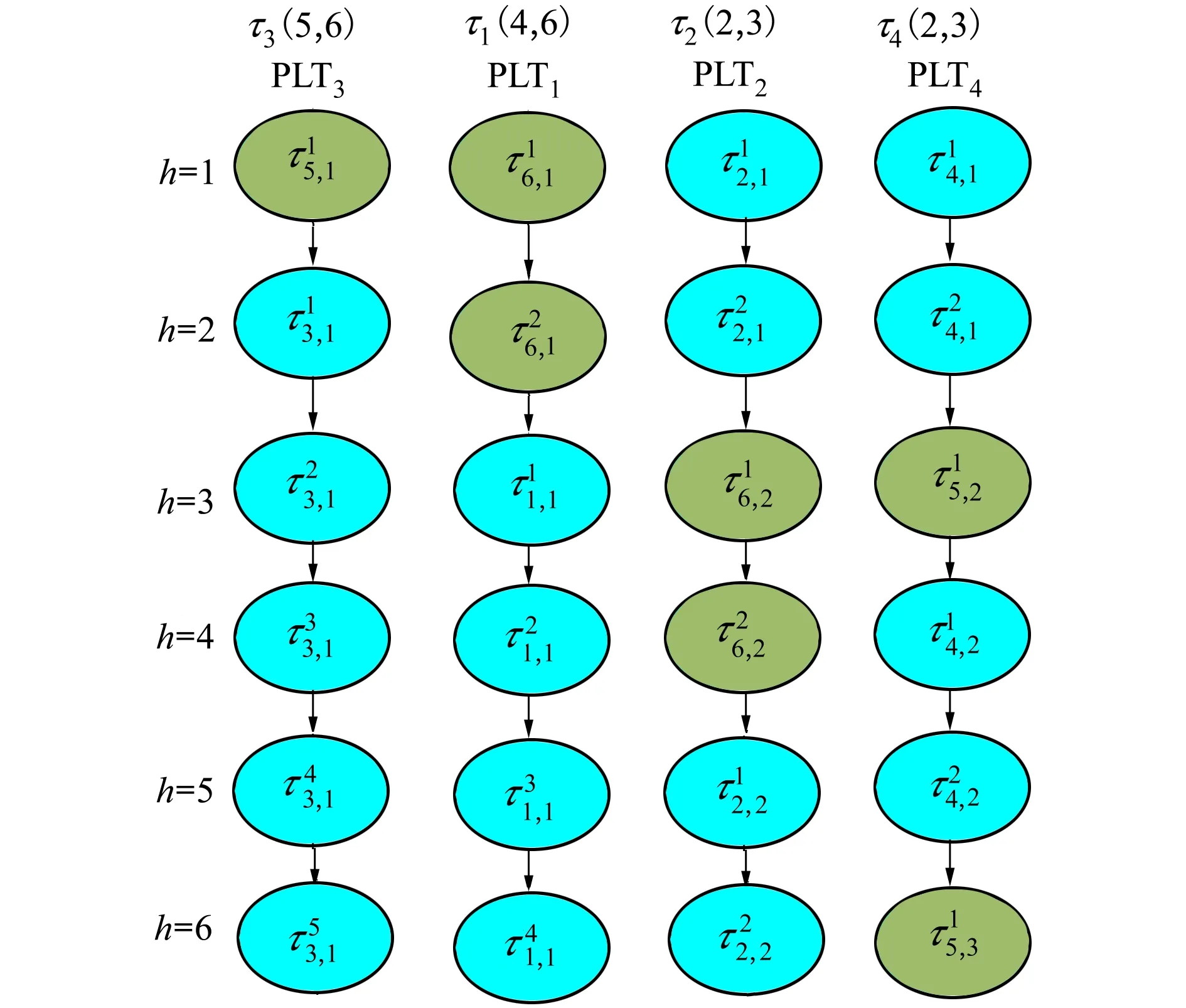
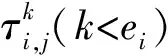
3 延遲因子及TLT-PLT轉化方法
3.1 延遲因子確定
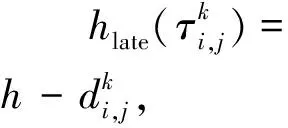
3.2 TLT-PLT轉化算法
3.3 處理器預分配算法
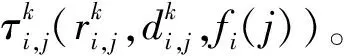
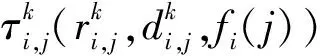
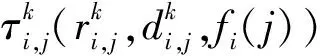
3.4 應用實例處理器分配結果

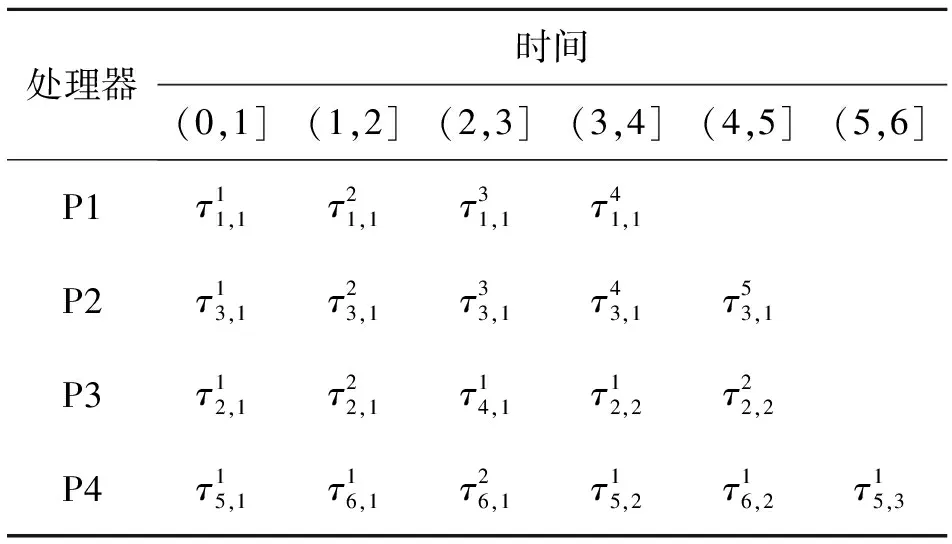
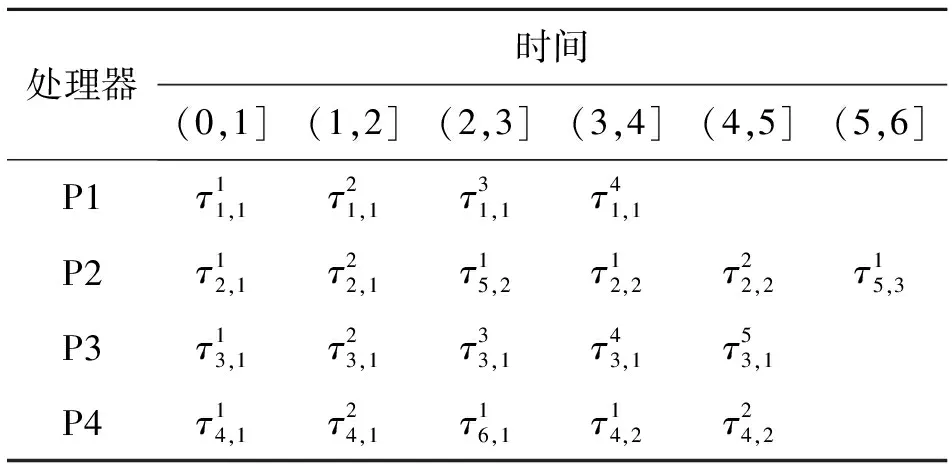
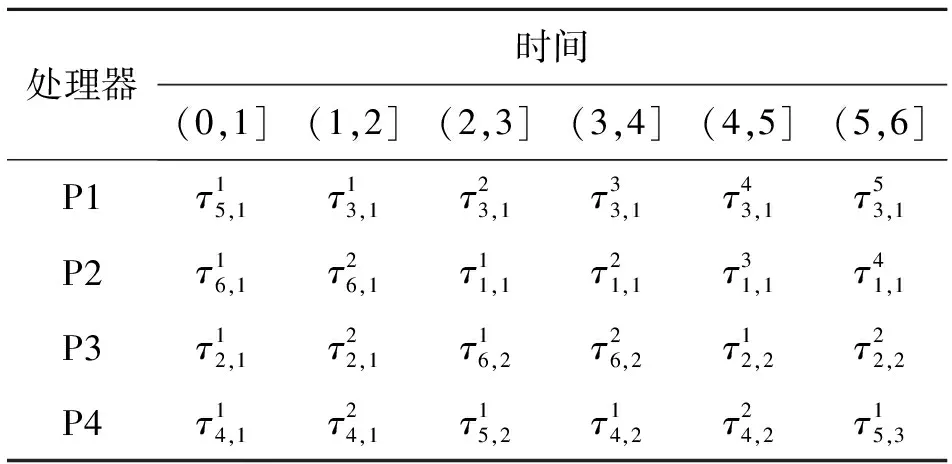
4 實驗及結果分析
5 結 論

