高精度室內融合定位算法研究

黃 健，楊國偉*，胡起立，畢美華，李 晶，李 娜

(1.杭州電子科技大學 通信工程學院，浙江 杭州 310018；2.杭州海關技術中心 環境與化學安全檢測研究所，浙江 杭州 311200；3.中國電子科技集團公司航天信息應用技術重點實驗室，河北 石家莊 050081)

0 引言

近年來，隨著無線通信技術的迅速發展，基于位置的服務在各個領域中都爆發出急速增長的需求，精確定位技術開始廣泛地應用于各個領域。室內定位作為導航定位的“最后一公里”，一直是研究機構和企業關注的熱點[1]。近十多年來，大量的新興技術如地磁、WiFi、藍牙、射頻識別、可見光[2-3]和超聲波等相繼應用于室內定位，但是這些技術都有各自的局限性，很難實現在實際復雜多變場景中的高精度定位。近年來，超寬帶(Ultra-Wideband，UWB)技術因具有很高的分辨率和很強的抗多徑能力能實現高精度測距而受到廣泛關注。

事實上，在非視距(Non-Line-of-Sight,NLOS)室內環境中，由于障礙物的遮擋會導致UWB定位精度急速下降，因此單一的室內定位方式仍然難以在復雜的室內環境中實現穩定且高精度的定位。慣性導航技術作為自主導航技術[4]，可以輔助UWB技術渡過NLOS的室內環境。又由于低成本的微機電系統(MEMS)慣性傳感器的精度難以匹配傳統慣性導航算法，所以需要采用行人航位推算(Pedestrian Dead Reckoning，PDR)算法來代替傳統的積分方法。但MEMS慣性傳感器的誤差隨著系統運行時間增加，會出現較大的誤差累積情況。為解決單一定位技術在室內定位時的不足，眾多學者提出采用融合定位方式完成室內定位。文獻[5]實現了WiFi與慣導結合的室內定位系統，但定位精度仍相對較低。文獻[6]將慣導定位與地圖結合實現手機端的室內定位，但是要求正常持握手機姿態，實用性不好。文獻[7]對WiFi和PDR室內組合定位進行了研究，通過無跡卡爾曼濾波算法融合二者定位數據,但定位精度仍受限于WiFi定位精度。文獻[8]使用擴展卡爾曼濾波融合UWB和PDR數據，但無法校準航向角誤差。

本文基于融合定位的思想，充分利用UWB和PDR各自的優勢，提出一種基于UWB與PDR的新型融合定位方法。在NLOS環境中，UWB定位產生了較大誤差甚至無法定位時，借助PDR減少因為NLOS而產生的定位誤差，同時可以借助UWB高精度的定位信息來消除PDR誤差累積。本文重點聚焦了二者融合定位過程中的主輔切換方法和補償方法，實驗證明本文方法的定位軌跡更加貼近真實軌跡，有效地降低了NLOS定位誤差，提高了室內定位的性能。

1 UWB定位模型

1.1 UWB測距原理

本文UWB測距采用簡單高效的TOA技術方案[9]。由于基于TOA的測距通常需要基站與標簽之間時間同步，而精確的時間同步實現難度大。UWB測距首先采用了單側雙向測距(SS-TWR)，該方法通過信號在標簽與基站之間的來回傳輸，避免了標簽與基站之間的時間同步問題，測距流程如圖1所示。

(1)

該SS-TWR方法沒有標簽與基站的時間同步問題。但是，由于標簽與基站之間存在微小的時鐘偏移，如果標簽和基站的時鐘偏移分別為eA和eB，則飛行時間誤差為：

(2)

由式(2)可以看出，飛行時間的誤差隨著Treply增加而增加，并且同設備的時鐘偏移也有關系。所以SS-TWR的精度也不夠高，因此提出了一種改進雙向測距法——雙邊雙向測距(ADS-TWR)[10]。

ADS-TWR方法是SS-TWR的升級改進版本，測距流程如圖2所示。

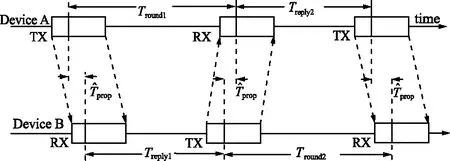
圖2 ADS-TWR測距流程Fig.2 ADS-TWR ranging process

(3)

誤差分析如下：

(4)

由式(4)可以看出，ADS-TWR的誤差與延遲時間Treply無關。同樣的時鐘差，ADS-TWR比SS-TWR的誤差小很多，可以得到更高的測距精度。獲得測距距離后，由于UWB模塊出廠時天線就存在接收信號延遲的問題，對UWB模塊進行測距修正，以提高實際使用中的測距精度。

1.2 UWB定位與天牛須搜索算法

在無線傳感器網絡定位算法中，全局搜索算法越來越受到關注。全局搜索算法將尋常三維定位的非線性方程組求解問題轉化為最優化問題，在很多領域得到成功應用[11]，本文嘗試將天牛須搜索(Beetle Antennae Search，BAS)算法應用到UWB定位算法中。

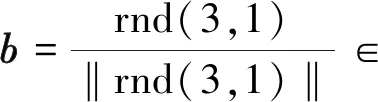
(5)

(6)

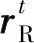
st=cδt，

(7)

δt=ηδt-1,

(8)

下標r，l表示右側和左側；上標t表示第t次迭代；δ為天牛的步長；c為質心到須的距離與步長之間的系數；η為步長衰減系數。天牛在t時刻的坐標為：

(9)

式中，sign(·)為符號函數。BAS算法的整體流程如下：

① 設置算法的迭代次數、初始步長和步長的衰減系數，并隨機生成天牛的初始位置。

② 隨機生成單位向量b，根據式(5)和式(6)計算天牛左須和右須的坐標和適應度函數，沿著較好方向前進，并更新下一次迭代使用的搜索范圍和步長。

③ 根據式(9)，經過迭代不斷更新天牛的空間坐標并更新最佳值。

④ 判斷是否達到最大迭代次數或全局最優解的適應值是否滿足最小界限，若未達到轉到步驟②。

將BAS算法應用到UWB定位的關鍵就是設置適應度函數(食物氣味強度)。f(x)為本文設計的適應度函數，表示為：

(10)

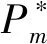
2 PDR模型

PDR算法是慣性導航的一種簡化算法，在慣性傳感器精度不高時，利用人走動產生周期性變化的特點，估計出人行走的步數和步長，再獲得每一步的航向角即可以求解出人行走前后的相對位置。PDR定位原理如圖3所示。

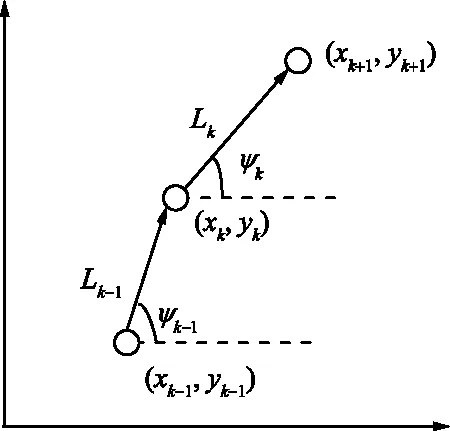
圖3 PDR定位原理Fig.3 PDR positioning principle

若(xk,yk)為人的當前位置，Lk為估計的步長，ψk為行走的航向角，則行人下一步的位置(xk+1,yk+1)可以通過下式求出：

(11)

PDR算法需要知道開始第一步的具體位置和方向，由此推算出后面行走的相對位置。所以步態檢測、步長估計和航向估計是PDR算法的3個核心步驟。

2.1 步態檢測

因為偽波峰的存在，傳統的基于閾值峰值檢測法會出現漏檢或誤檢的情況，本文采用了一種基于時間周期性的峰值檢測法作為步態檢測的方法[13]。當人在行走時，每一步都可以看成一個周期，并且每一步相隔的時間都應該差不多，所以可以利用該特點并結合峰值檢測法來進行步態檢測。

首先，通過傳統的波峰檢測法求得第1個波峰與第2個波峰相隔的時間，記為t1，根據加速度的周期性變化原理，第2個波峰與第3個波峰之間的相隔時間也大概為t1，因此可以在第2個波峰之后的t1時間附近尋找第3個波峰，找到第3個波峰之后更新相隔時間，以此類推找到所有波峰點。計算如下：

(12)

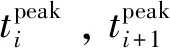
(13)

式中，δ為波動參數，可由實驗測試進行估計。為了保證每一步的周期具有強的相關性，每一步后要對Ti進行更新。最后，由于偽波峰的影響，經過篩選，在波動范圍內產生多個極值點，取這幾個極值點中波峰最大的點作為真正的波峰點。

2.2 步長估計

獲得步數后，要估計對應每一步的長度。因為每個人的生理狀況不一樣，步長也因人而異。當然，同一個人在行走過程中，每一步長度也有所不同，所以基于常數模型的步長估計很難適應實際情況。本文的自適應算法結合了基于加速度幅值變化非線性步長估計[14]和基于步頻的線性步長估計[15]，計算如下：

(14)

式中，α，β與人的生理因素有關，可由大量實驗得出，α取值在0.4～0.5，β取值在0～0.1；amax，amin分別表示該步周期內加速度的最大值和最小值；fk為對應的每一步的行走頻率；φ是一個常數。

由于噪聲的影響，加速度數據會引入噪聲誤差，所以要對采集的加速度數據進行濾波來消除噪聲，提高步態檢測的準確率。本文使用滑動平均濾波來降低噪聲信息。采用上述的步態檢測法和步長模型，并使用陀螺儀計算得到前進的航向角改變量，根據UWB前期準確定位的結果得到初始值，再通過式(11)就可以得到航位推算位置。

3 UWB和PDR融合定位

3.1 UWB NLOS定位場景判定和優化

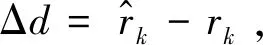
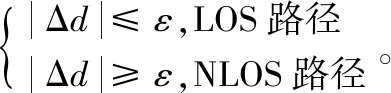
(15)

由于濾波器的遞推作用，受NLOS污染嚴重而偏差較大的坐標值不僅使當前時刻的坐標值估計發生較大偏差，并且由于卡爾曼濾波器的記憶性，使后續的坐標估計都受到嚴重影響，對于這些不準確的坐標點，應當舍棄。在被舍棄的點上，用狀態預測值代替狀態估計值，所以本文引入偏移卡爾曼濾波器消除NLOS誤差[17]。當濾波過程中沒有進入NLOS場景，卡爾曼濾波則正常迭代；若進入NLOS場景，通過把卡爾曼增益設為0來舍去這個測量值，并用狀態預測值來代替狀態估計值。x軸定位數據的卡爾曼濾波如圖4所示，當沿著y軸方向運動時，坐標x軸數據變化較小，門限值選取合理，該方法對x軸坐標NLOS誤差抑制明顯。

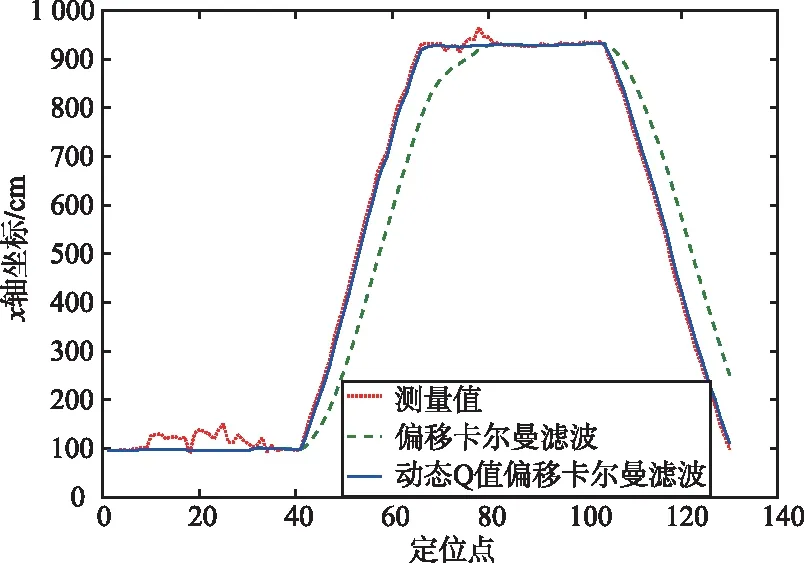
圖4 x軸定位數據的卡爾曼濾波Fig.4 Kalman filter of x-axis positioning data

但是當運動方向改變，沿著x軸方向運動時，濾波模型發生變化，若濾波器的參數保持不變，x軸數據變化過快時，將影響正常濾波，嚴重時甚至造成濾波發散，這時必須改變濾波器參數增強濾波收斂效果。數據急速變化時，可以通過增加過程噪聲Q值，Q值越大，代表越信任實際測量值，以提高此段的跟蹤能力，從而促使該段估計值能較快收斂，但Q值也不能太大，當Q值太大時濾波數據將基本與實際測量值相等，無法做殘差判斷。由圖4可以看出，改變了Q值的偏移卡爾曼濾波能更好地適應數據急速變化的情況。只通過x軸的殘差數據Δdx來判斷NLOS場景是不夠的，對y軸數據也做相同處理得到殘差數據Δdy，對二者做聯合判斷，2個殘差值只要有一個大于閾值ε就可以判定進入NLOS場景。

通過濾波器來更好地獲取運動方向的變化，其關鍵是需要實現動態地取Q值。可以利用PDR的航向角來輔助濾波器動態地取Q值。PDR定位是一種相對定位方法，開始定位時需要獲得PDR的初始坐標點和初始航向角。PDR的初始位置可由UWB定位的坐標獲得，PDR航向角初始值由初始時刻UWB的N個準確定位結果的位置共同決定。如果只選用UWB的2個定位結果獲得的初始航向角，初始航向角有時會因為定位的波動產生較大的誤差。因為UWB數據獲取頻率通常是大于PDR每一步的頻率，所以在PDR進行第一步定位前有N個UWB定位數據。對這N個數據做線性擬合[18]，得到的直線斜率作為PDR初始航向角，減少定位波動對初始航向角的影響。N的值由實際UWB的采樣頻率和實際場景決定，本文N值取4。獲得PDR的初始坐標和初始航向角后，就可以獲得PDR每一步的坐標和航向角，知道大概的運動方向。考慮x軸坐標為濾波對象，當PDR的航向角與x軸的夾角在90°附近時，數據變動較小，這時Q值可以取較小的值。當PDR的航向角與x軸的夾角在45°附近時，數據變動較平緩，這時Q值可以取適中的值；當PDR的航向角與x軸的夾角在0°附近時，數據變動較大，這時Q值可以取較大的值。當濾波對象為y軸坐標時，方法同上。所以，可以根據PDR的航向角值θ來動態地對Q賦值。本文通過給定的3個Q值：Q1，Q2和Q3，來覆蓋整個角度范圍(0°,360°)。Q1，Q2，Q3值根據實際數據和濾波情況來確定，本文設置的濾波器R=0.542，Q1=1，Q2=0.4，Q3=0.05，則有：

(16)

式中，QX為x軸坐標濾波器Q值；QY為y軸坐標濾波器Q值。

3.2 PDR誤差累積修正和融合定位

由于PDR定位存在累積誤差，特別是較大角度的拐彎會對PDR航向角造成較大的影響。UWB是一種絕對定位方式，可以通過UWB定位對PDR的航向角進行修正[19-20]。首先，設定航向角變化閾值H，當某一步相較于初始航向角的航向角變化超過閾值H時，認為PDR航向角累積誤差過大，對這一步的PDR定位進行UWB定位替代，用UWB估計的方向取代PDR的當前航向，用UWB定位坐標作為PDR的初始坐標。若UWB定位剛好處于NLOS場景，先不修正，等到UWB定位離開NLOS場景時，再對PDR定位進行修正。

獲得UWB優化后的定位數據、NLOS情況和誤差累積修正的PDR數據后，要對二者數據進行融合。在LOS場景，直接以UWB濾波優化后的定位數據作為定位結果；在NLOS場景，UWB定位數據會有較大的誤差，因此舍棄UWB定位數據，以誤差累積修正后的PDR的定位數據代替在NLOS場景中UWB的定位數據，將PDR定位數據作為NLOS場景中的定位結果。

4 實驗結果與分析

4.1 UWB定位測試

測試在2個場景進行：一個是杭州電子科技大學1教428教室，該場景無遮擋，不存在NLOS情況；另一個是杭州電子科技大學1教架空層，遮擋場景多，存在NLOS情況。測試設備包括4個UWB基站和1個自主設計的高精度定位系統，該系統包括用于UWB定位的DW1000模塊和用于PDR定位的MPU9250慣導模塊，實驗測試數據通過4G模塊上傳到云端。測試設備及測試環境如圖5所示。

(a) 定位裝置

(b) UWB基站

(c) 教室場景

(d) 架空層車庫場景

進行定位實驗前，首先對UWB模塊進行測距修正。在LOS環境下測距誤差可以通過調整UWB模塊的天線延時參數來降低。在LOS環境下，以0.6 m的間隔獲得各個點的測距值，再利用最小二乘法求得一個修正值,使各個點修正后的測距值與真實距離值的差值平方和最小，最后將該修正值除以光速轉換成天線延時參數輸入到UWB模塊中。測距修正前后數據如表1所示。測距修正前，平均測距誤差為21.19 cm；測距修正后，平均測距誤差約為3.9 cm。

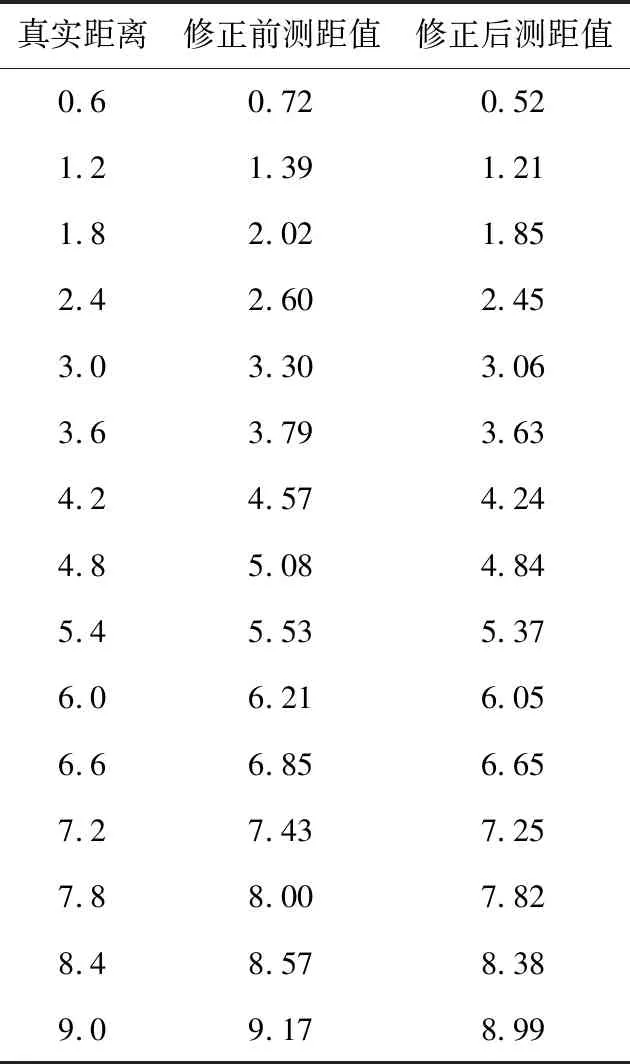
表1 UWB測距值

在教室場景中布置的4個UWB基站坐標分別為(0,0,2.4)，(9.25,0,2.4),(8.95,11.7,2.4)，(-0.1,11.5,2.4)，在車庫場景中布置的UWB基站坐標分別為(0,0,1.8)，(16.8,0,1.8)，(16.8,25.2,1.8)，(0,25.2,1.8)，接著選定幾個測試坐標進行自主設計定位系統的UWB定位測試，分別用測距未修正最小二乘法算法、測距修正最小二乘法算法和測距修正BAS算法進行定位并對結果進行比較。因為測距精度的限制，UWB定位的z軸定位誤差較大，所以通常UWB定位只關注x軸和y軸的定位精度，本實驗UWB定位也只考慮了x軸和y軸的二維平面定位精度，并以定位坐標與真實坐標的歐式距離來衡量定位精度，定位結果如圖6所示。

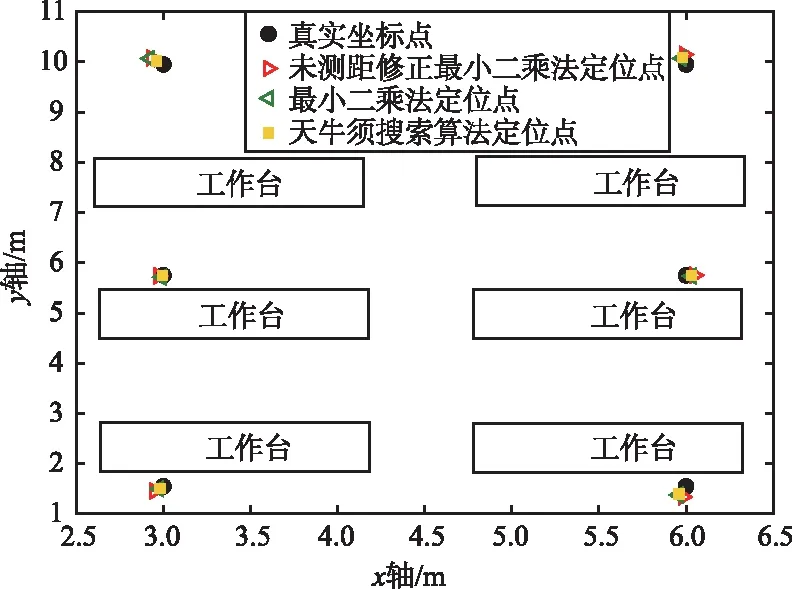
(a) 教室定位示例

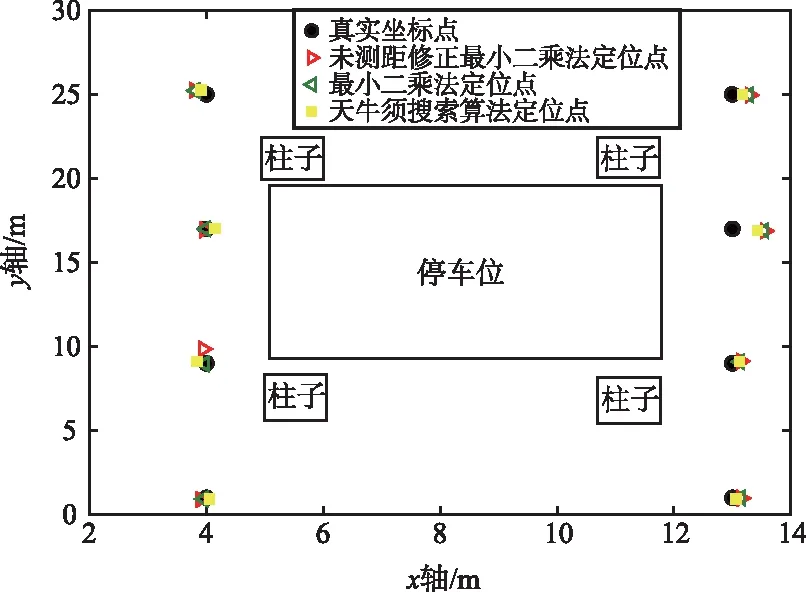
(b) 架空層定位示例

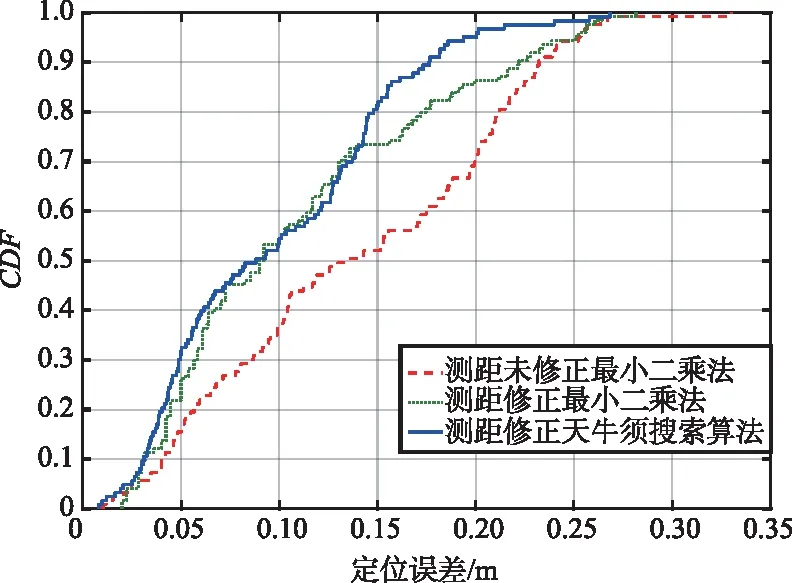
(c) 定位誤差累積分布函數(CDF)

在教室場景中，測距未修正最小二乘法的平均定位誤差約為13.79 cm，測距修正最小二乘法的平均定位誤差約為10.96 cm，而測距修正BAS算法的平均定位誤差約為9.65 cm。在地下車庫場景中，測距未修正最小二乘法的平均定位誤差約為22.05 cm，測距修正最小二乘法的平均定位誤差約為19.63 cm，而測距修正BAS算法的平均定位誤差約為16.65 cm。可見，在場景遮擋情況少、定位結果較好的情況下，BAS算法雖然也提升了定位精度，但是提升不大。而在場景遮擋情況嚴重、定位結果較差的情況下，該優化算法的提升效果較好。

4.2 PDR定位測試

首先對本文PDR算法的步態檢測和步長估計進行評估。進行步態檢測評估時，分別走了20，50，100步，再用基于閾值的峰值檢測法和基于時間周期性的峰值檢測法進行比較，實驗結果如圖7所示。由圖7可以看出，基于時間周期性的峰值檢測法相較于基于閾值的峰值檢測法精度更高，提升了約5%的精度。進行步長估計評估時，控制每一步的步長都保持在60 cm，再用本文的自適應步長估計算法同經典的基于加速度幅值變化非線性步長估計進行對比，實驗結果如圖7(d)所示，可以看出本文的自適應步長估計算法精度更高。

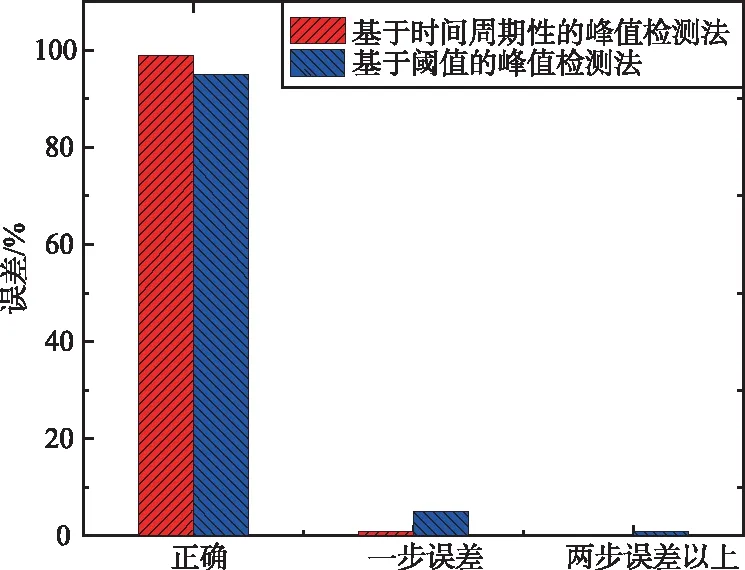
(a) 真實步數為20

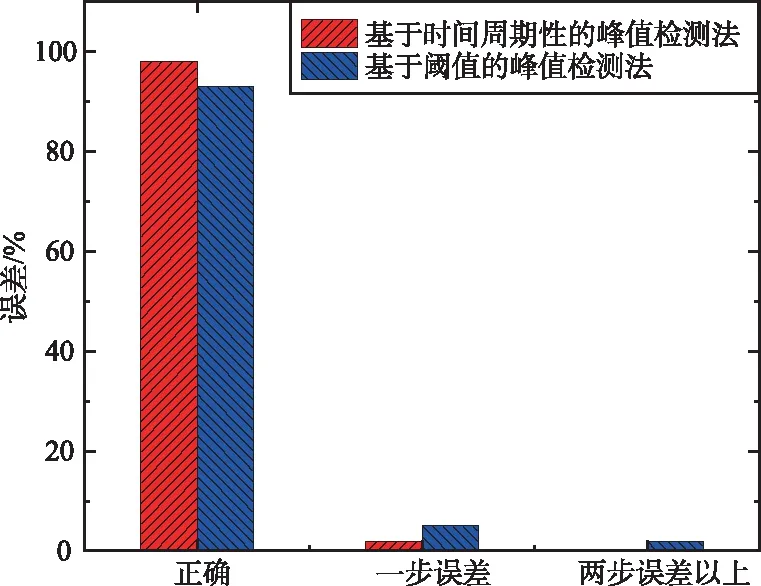
(b) 真實步數為50

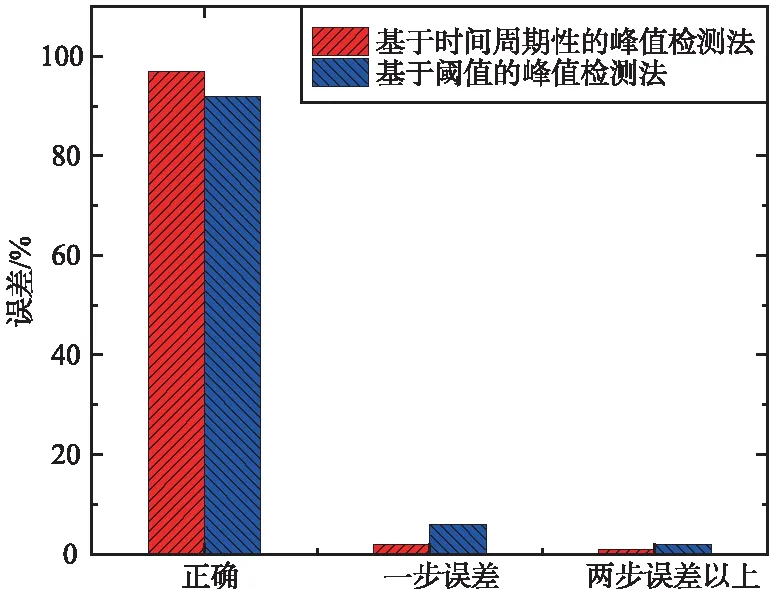
(c) 真實步數為100

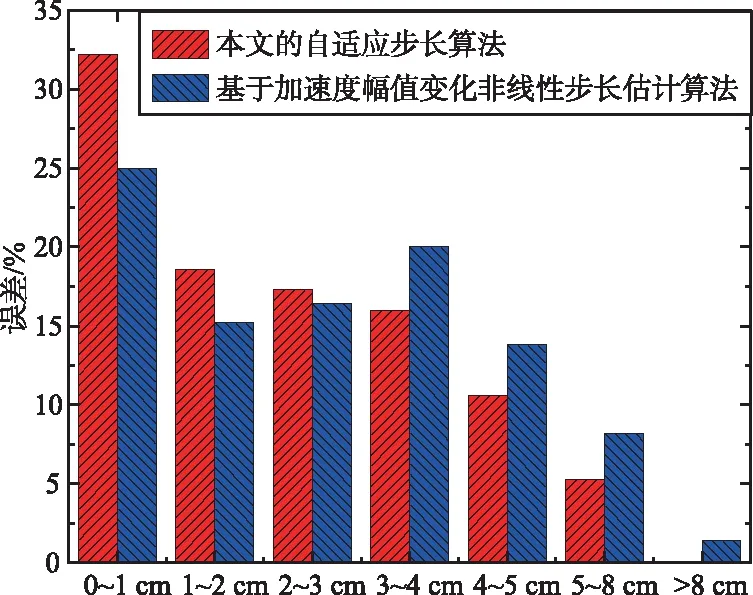
(d) 步長誤差分布

PDR實驗在杭州電子科技大學1教的架空層車庫進行測試，設定起點坐標為(0,0)，沿著(0,0)，(0,25.3)，(-8.3,25.5)，(-8.3,0)，(0,0)的路線行走，通過定位系統上慣性傳感器模塊的數據采集，對數據進行處理，再用本文的PDR算法進行軌跡計算，實驗結果如圖8所示。可以看出，在開始階段PDR定位能達到較高的精度，定位誤差能保持在20 cm以內。隨著時間的推移，由于誤差累積，特別是拐角的影響，定位誤差逐漸增大，最后的定位點與實際點的誤差達到74 cm，所以PDR單獨定位時適合短時間且拐彎較少的場景。

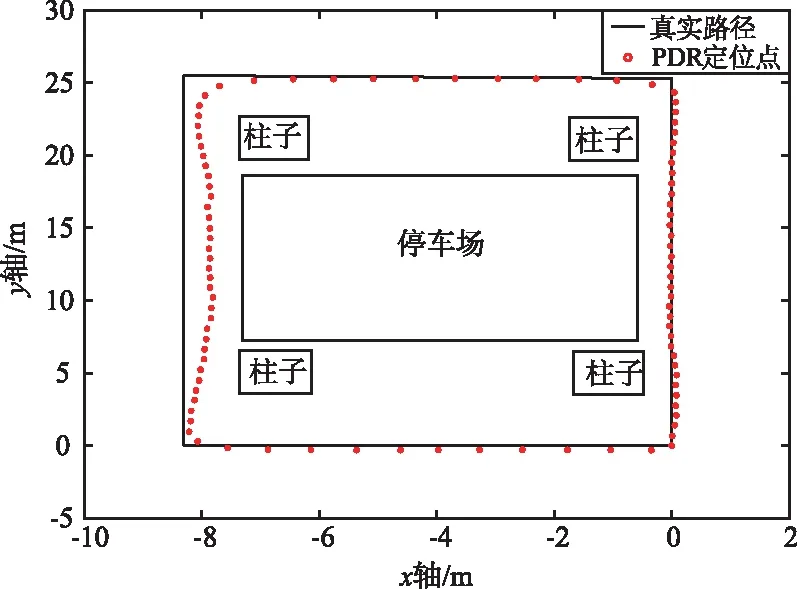
圖8 PDR定位實驗結果Fig.8 Diagram of PDR positioning test

4.3 UWB和PDR融合定位

融合定位實驗在杭州電子科技大學1教的架空層車庫進行測試。測試場景如圖9所示，中間有2根柱子作為遮擋來創造NLOS環境。

圖9 融合定位測試場景Fig.9 Environment of fusion positioning test

首先布置4個UWB基站，其坐標分別為(0,0,1.8)，(0.4,16.9,1.8)，(9.3,0.05,1.8)，(8,16.25,1.8)，并設定起點坐標為(1,1)。沿著(1,1)，(1,14)，(9.3,14)，(9.3,1)，(1,1)的路線行走，同時開啟UWB和PDR定位，UWB定位采用上述的BAS算法，PDR定位采用上述的PDR算法，并對二者的定位進行數據融合。本文的融合算法針對UWB NLOS區域，在LOS區域仍采用UWB定位，定位結果如圖10所示。由圖10可以看出，由于柱子遮擋的影響，UWB定位在2個NLOS處產生了較大的定位誤差，PDR定位在剛開始時誤差也較小，但是經過了2次90°拐彎，航向角產生了約5%的偏移，本文融合定位算法的定位軌跡誤差更小，也更接近實際真實軌跡。本文各種定位方式的誤差如下：在NLOS場景中，UWB的平均定位誤差為42.8 cm，PDR的平均定位誤差為17.2 cm，融合定位的誤差為13.7 cm。本文的融合算法較好地利用了2個系統各自的特點，有效地抑制了NLOS干擾，提高室內定位整體準確性和可靠性。

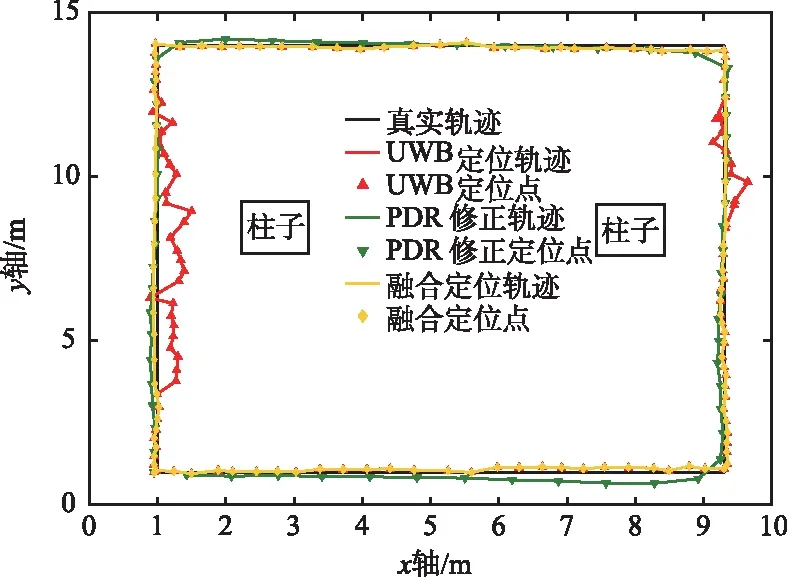
圖10 UWB和PDR融合定位實驗結果Fig.10 UWB and PDR fusion positioning experiment

5 結束語

本文對UWB和PDR室內定位算法進行獨立和融合的改進研究。首先將BAS算法應用到UWB定位中，在無遮擋和有遮擋情況下開展定位實驗測試，精度分別提升至9.65，16.65 cm。然后將基于時間的周期性的峰值檢測法和自適應步長估計應用到PDR定位算法中，實驗測試結果顯示，在最初30 m以內和一個拐彎的情況，精度在20 cm左右，但隨著距離增加和拐彎增多，精度下降較快。盡管上述2種改進方法都在一定情況下提升了各自定位精度，但仍無法解決UWB定位NLOS和PDR定位累計誤差的問題。針對這2個問題，提出了一種基于UWB和PDR技術的融合定位算法，根據基于PDR航向角動態改變過程噪聲Q值的偏移卡爾曼濾波法來判別NLOS情況，利用了UWB定位修正PDR累積誤差，同時利用了PDR定位修正UWB在NLOS下的定位誤差。實驗測試結果顯示，所提出的融合定位算法有效地降低了NLOS情況下UWB的定位誤差，平均定位誤差降至0.137 m，比單一UWB定位精度提升了約68%，對于地下停車場、倉庫和商場等大型室內場所的長時間、高精度定位具有一定的參考價值。