基于Wiener過程退化模型的高壓閥壽命預測

張子劍，趙佳琳，常增柱，唐 慶

（1.河北工業大學 經濟管理學院，天津 300401；2.天津航海儀器研究所，天津 300091；3.中國船舶工業綜合技術經濟研究院，北京 100081）

0 引言

高壓閥作為深海化作業的關鍵部件之一，廣泛應用于海軍裝備系統中，用來控制艦船載水倉與外界海水的交流。與常規環境條件相比，高壓閥在深海極限環境條件下，具有工作壓力大、密封要求高、材料抗腐蝕能力強等特點，其可靠性直接影響海軍裝備的性能發揮。因此，探索高壓閥的壽命預測對深海海軍裝備的發展意義重大。

目前，Wiener過程模型是基于性能退化數據可靠性評估模型中應用最廣的模型之一，可以更好地描述退化過程中存在的不確定因素。Tang 等[1]通過退化軌跡以及偽失效閾值，得到了退化模型的偽壽命數據，建立了Wiener過程退化模型，并提出一種改進的極大似然估計法來估計可靠度函數中的未知參數。Ye等[2]結合非線性退化數據，在原Wiener過程退化模型的基礎上，提出帶測量誤差的Wiener過程退化模型。王小林等[3]結合非單調退化數據，提出了分階段Wiener-Einstein退化模型。彭寶華[4]給出了一元和多元Wiener過程建模的可靠性評估模型，并采用貝葉斯法對模型中的未知參數進行評估。根據Wiener過程的首達時間服從逆高斯分布，王泰[5]建立了漂移參數和擴散參數均為恒定值的Wiener過程退化模型。楊斌[6]提出一種基于Wiener 過程考慮關鍵性能退化數據的評估模型。張云等[7]針對數控轉臺性能退化過程較為緩慢且存在波動的特點，采用Wiener過程進行數學建模。齊建軍等[8]基于Wiener過程，建立了以累積工作時間和備用時間為自變量模型，對加注泵進行了壽命預測。

傳統的壽命預測方法主要依賴于產品的壽命數據[9]，而高壓閥屬于高可靠、長壽命產品，往往很難在可行的時間內完成壽命試驗，獲得足夠的壽命數據信息。通過對高壓閥失效機理的分析得出，高壓閥在使用過程中性能是逐漸退化的，因此本文利用其退化數據建立退化模型進行壽命預測，考慮到數據的波動性以及個體間的差異性，將Wiener過程引入退化模型，可以較好地預測產品的真實退化過程。

1 Wiener 過程評估模型

1.1 一元Wiener 過程

一元Wiener過程的定義為

式中：x(t,μ,σ2)是t時刻退化量的測量值；μ是漂移系數，是用來描述性能退化率的參數；σ是擴散系數，用來描述退化過程中的波動性；B(t)是標準的布朗運動。

結合一元Wiener過程的定義可得，對于任意時刻t，退化量增量的均值和方差分別為

由式（2）和（3）可看出，退化量的均值和方差隨時間的增加而增大，其變異系數，變異系數隨時間的增加而減少，表明樣本的退化路徑是隨時間的增加越來越接近平均退化曲線。

1.2 建立評估模型

若產品的某性能退化指標的退化過程服從式（1）的Wiener過程，失效閾值確定為Df，產品壽命T表示退化量X第一次達到Df的時間，具體表達式如下：

式中，inf表示函數下界，結合Wiener過程模型所表現出的性質，T在實現了函數變化后服從的壽命分布屬于逆高斯分布。當式（1）中t=T時，即X(t)服從Wiener過程退化軌跡模型時，產品的壽命T服從逆高斯分布，即得到對應的失效函數和失效概率密度函數分別為

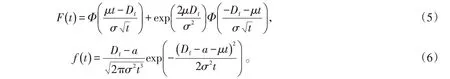
當Df＞a，即性能退化量逐漸增加時，產品的可靠度函數為[10]

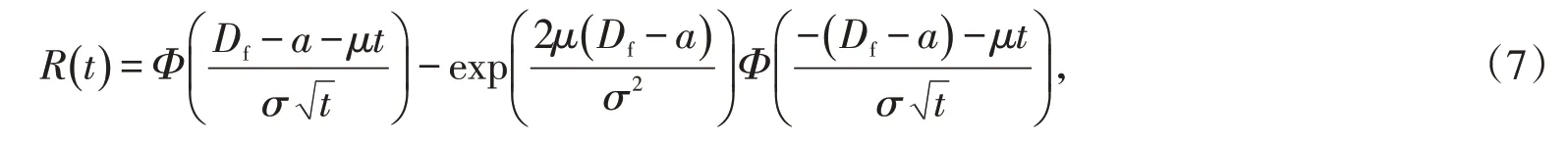
式中，Φ為正態分布函數。

2 Wiener 過程模型參數估計

2.1 模型參數估計

根據式（1）中Wiener過程模型得到

式中：Δxi=xi-xi-1,Δti=ti-ti-1,ΔΒi=Βi-Βi-1,i=1,2,…,N。由于ΔΒ(ti)～N(0,Δti)，則

由式（10）以及Wiener過程的退化增量具有的獨立性，得到其似然函數為

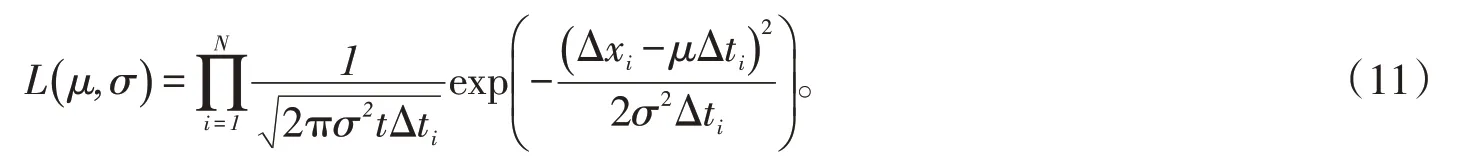
對式（11）取對數，得到

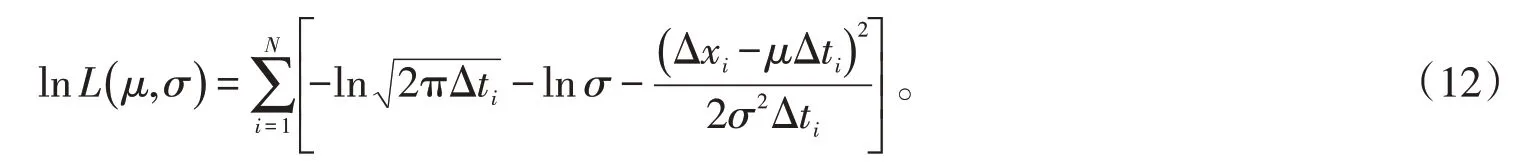
分別對μ和σ求偏導，得到

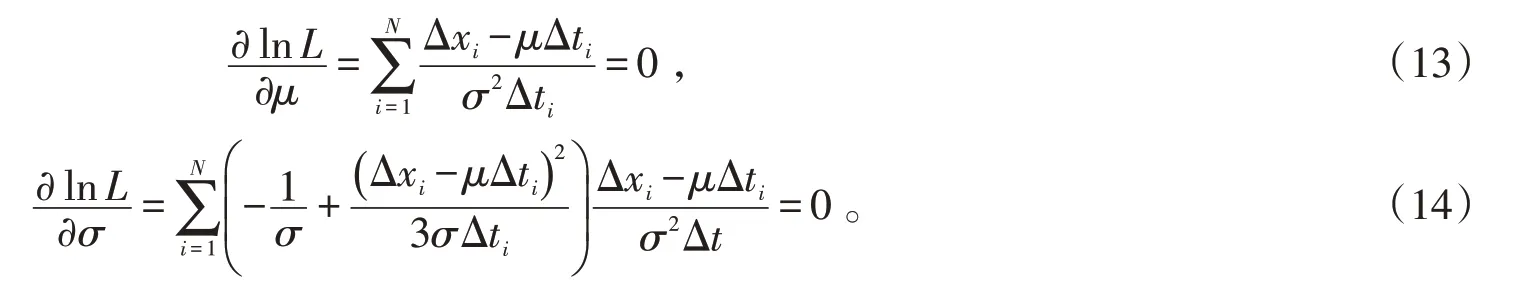
由此可知：

2.2 模型參數分布假設

在參數估計時，如果將Wiener過程模型中的未知參數都假設為恒定值，計算簡便，但是會忽略不同樣本間的差異性。如果假設每個參數的分布都為正態分布，求解會非常復雜。綜合考慮以上因素，根據各個參數之間的不同，將差異性、波動性較大的參數假設為正態分布，其余參數近似為常數[11]。

模型選取變異系數Cv()X作為確定各參數差異大小的定量指標。變異系數可以衡量參數的變化程度[12]。當比較2個或多個指標的變化程度時，如果計量單位與平均值相同，可以直接比較標準差；如果兩者不同，則需要計算變異系數以消除數據的絕對大小對變異程度的影響。樣本間數據差異越小，則變異系數越小。

概率密度函數為

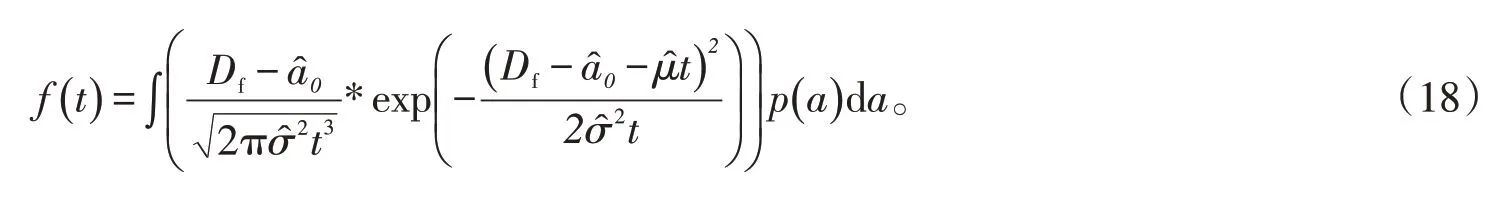
3 實例驗證

3.1 失效機理分析

J941H-64型“大、潛、深”電動截止閥主要有截止閥閥體及其電驅動頭、控制系統組成，可以按照控制系統指定的動作幅度和頻率，自動實現閥門啟閉工作，結構如圖1所示。

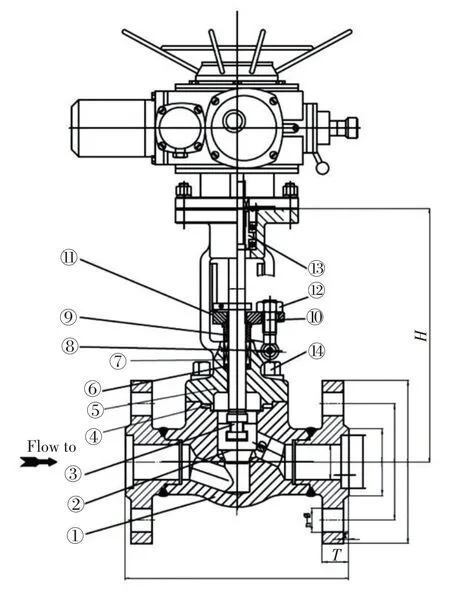
圖1 高壓閥結構圖Fig.1 High-pressure valve structure diagram

電動截止閥在海水中的作用是節流，通過對閥桿③施加一定的扭矩，沿軸的方向，向閥瓣②施加壓力，使得閥瓣密封面與閥座密封面④緊密貼合，阻止2個密封面之間的泄漏。

閥門失效的主要機理為由于閥瓣密封面與閥座密封面之間磨損，縫隙逐漸變大，導致失效[13]。高壓閥在使用過程中是一個逐漸退化的過程，數據存在波動性，個體間又存在差異性，因此為了描述退化過程中存在的這些不確定因素，將Wiener 過程引入退化模型。該模型可以較好地描述產品的真實磨損退化過程。

3.2 基于Wiener 過程的高壓閥的可靠性建模

3.2.1 建模步驟

基于Wiener過程的高壓閥的壽命預測步驟如下：

1）數據的預處理。整理得到需要的試驗數據，并進一步對采集到的高壓閥泄漏量的退化數據進行預處理；

2）利用極大似然估計法推導退化模型中漂移系數μ和擴散系數σ的參數估計表達式；

3）利用泄漏量退化的試驗數據，來求解漂移系數μ和擴散系數σ以及退化量初值a；

4）根據故障概率密度函數和可靠性函數表達式，代入確定的參數值，繪制失效概率密度曲線和可靠度曲線，并對高壓閥的剩余壽命進行評估[14]。

3.2.2 建模結果分析

對選取的電動截止閥進行可靠性壽命試驗，收集壽命試驗過程中的性能退化數據，包括閥門出入口壓力、閥桿力矩、應力應變以及泄漏量，當其中任何一項指標超出失效閾值時，表示閥門故障，此時記錄電動截止閥的失效時間為其實際壽命。選擇4 個閥門樣品，重復開展電動截止閥壽命試驗，收集壽命試驗數據。

實例選取泄漏量作為關鍵性能退化指標，受試樣本數為4，對4個試驗高壓閥每200 h測量一次泄漏量值。閥門啟閉周期內，泄漏量超過300 mL時，判定受試產品失效，此時終止試驗，該失效時間即為高壓閥壽命。終止試驗時4 個樣本的實際壽命如表1所示。

表1 高壓閥實際壽命Tab.1 Actual life of high-pressure valve

測量到的退化數據繪成退化軌跡如圖2所示。

從圖2 可以看出，隨著時間的增加，高壓閥的泄漏量呈現上升趨勢的同時伴有一定的波動性，符合性能逐漸退化的特點。因此，適合選用Wiener過程退化模型對其進行壽命預測。在泄漏量截止條件下，通過試驗數據測量方法獲得的退化數據量相對較大，不利于隨后的數據比較分析。因此取每個樣本試驗的前100 組數據來研究，利用這些測量數據對高壓閥進行評估，并與其實際壽命進行比較。

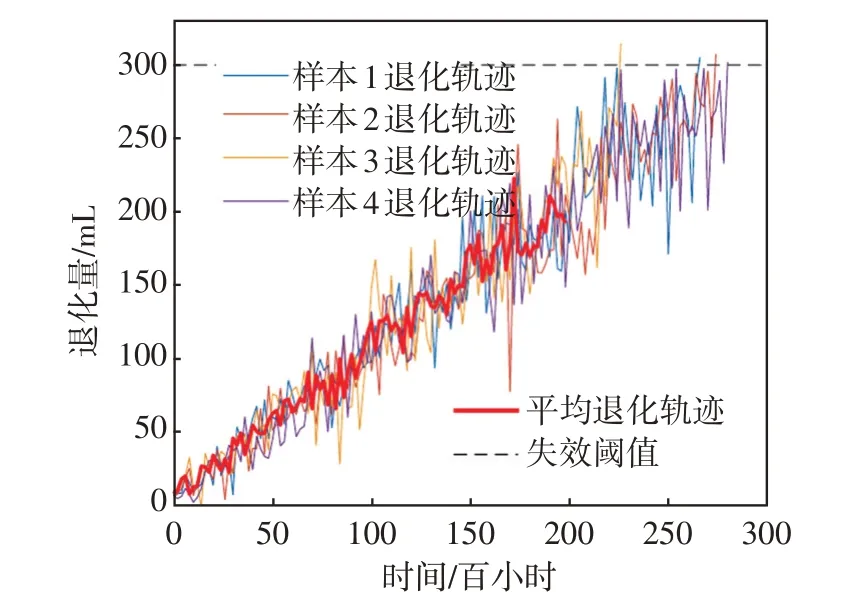
圖2 高壓閥泄漏量退化軌跡Fig.2 Degradation track of leakage volume of high-pressure valve

將前100 組數據代入式（15）、（16）中，計算出每個樣本出口壓力的見表2。根據表2 中4 個樣本的退化量初值、漂移系數、擴散系數，得到各參數的平均值，變異系數和標準差，見表3。

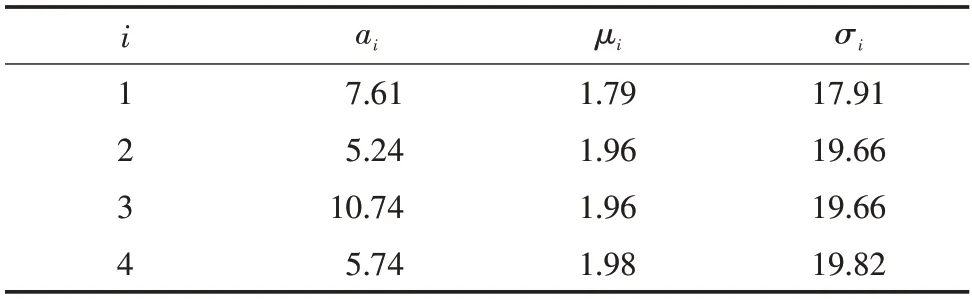
表2 退化量初值、漂移系數和擴散系數Tab.2 Initial value of degradation quantity,drift coefficient and diffusion coefficient

從表3可以看出，初值a的變異系數為0.58，初值的變異系數較大，因此假設初值a服從正態分布，漂移系數和擴散系數取其平均值。即則概率密度函數為

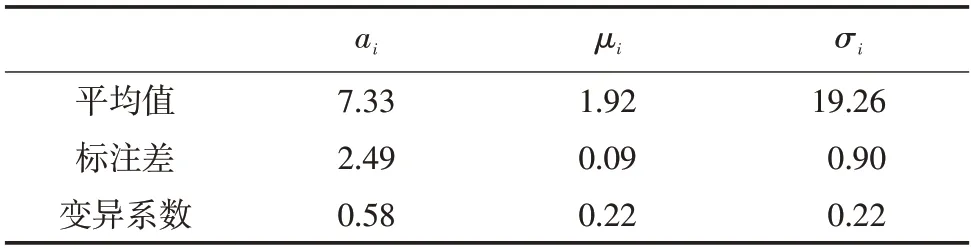
表3 參數的平均值、標準差和變異系數Tab.3 Mean value,standard deviation and variation coefficient of parameters

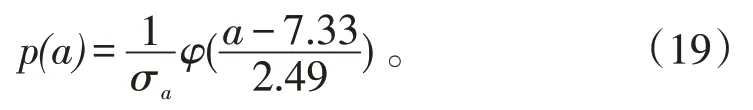
根據該型號高壓閥的技術要求，正常運行情況下，泄漏量不超過300 mL，即失效閾值Df=300 mL。將失效閾值和泄漏量的，代入式（17）可以得到高壓閥的可靠度函數為

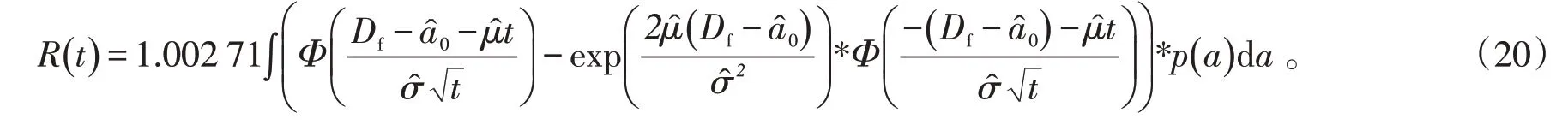
根據式（18）概率密度為

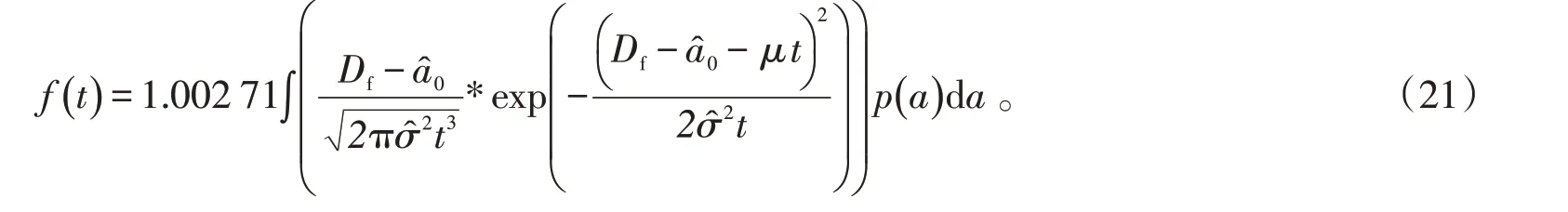
分別繪制可靠度函數和失效概率密度函數如圖3和圖4所示。

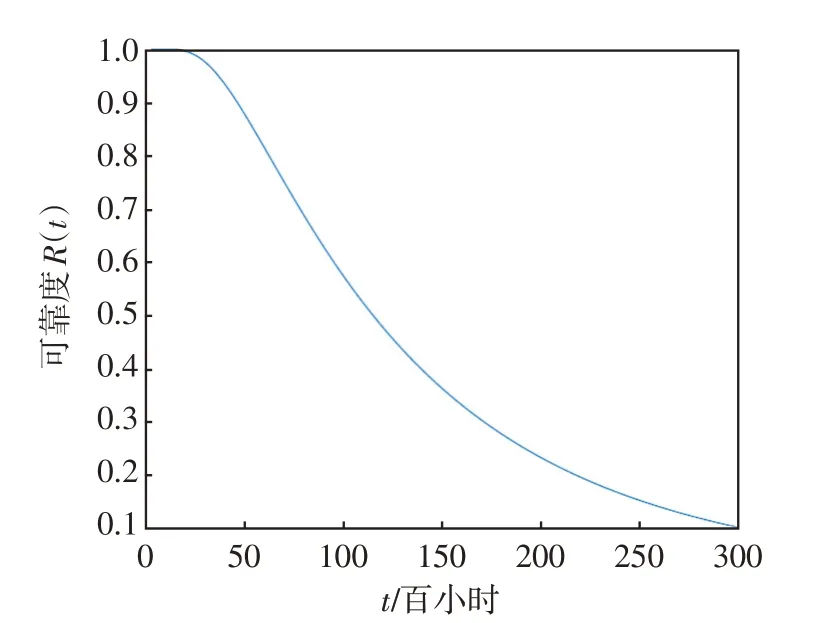
圖3 高壓閥可靠度曲線Fig.3 High-pressure valve reliability curve

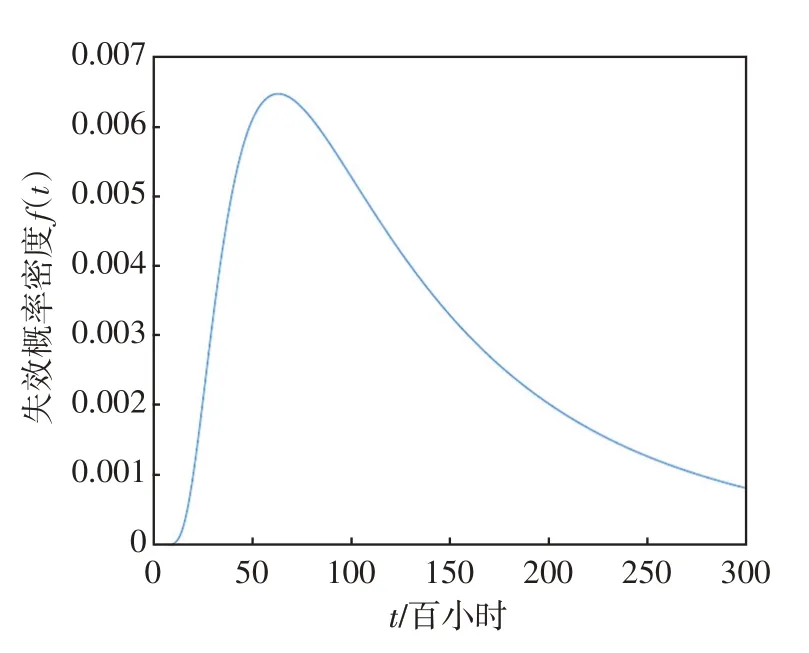
圖4 高壓閥失效概率密度曲線Fig.4 Probability density curve of high-pressure valve failure

從可靠度曲線和失效概率密度曲線可以看出，在最開始時，產品故障率非常低，到25 000小時基本失效，預測壽命值與4個樣本的實際平均壽命非常接近。因此，從預測結果來看，基于Wiener過程退化模型的預測符合實際情況。

3.4 壽命預測

為了說明本文提出基于Wiener 過程模型評估方法的準確性，下面將采用基于ARIMA 模型評估方法與之對比。

Wiener過程模型和ARIMA模型對壽命進行預測時，參數估計采用所有數據的整體效應，進而得到平均化的預測結果。在數據處理過程中，多次測量平均值可以減少誤差[15]。因此，在進行ARIMA模型預測時，將數據的平均退化軌跡進行預測、擬合，并與Wiener過程模型預測的結果以及產品實際壽命進行比較。

3.4.1 基于Wiener 過程模型的壽命預測

下面根據式（8），采用Wiener 過程模型對剩余壽命進行預測，為了減小預測誤差，選取4個樣本平均退化軌跡上的5 個時間點做剩余壽命分析，得到5個時間點的失效概率密度如圖5所示。

從圖5 中看出隨時間推移，剩余壽命不斷減少，到25 000 h基本失效，符合可靠度函數圖像，并且隨著預測數據的增多，失效概率密度越來越集中。計算出各個點的剩余壽命如表4所示。

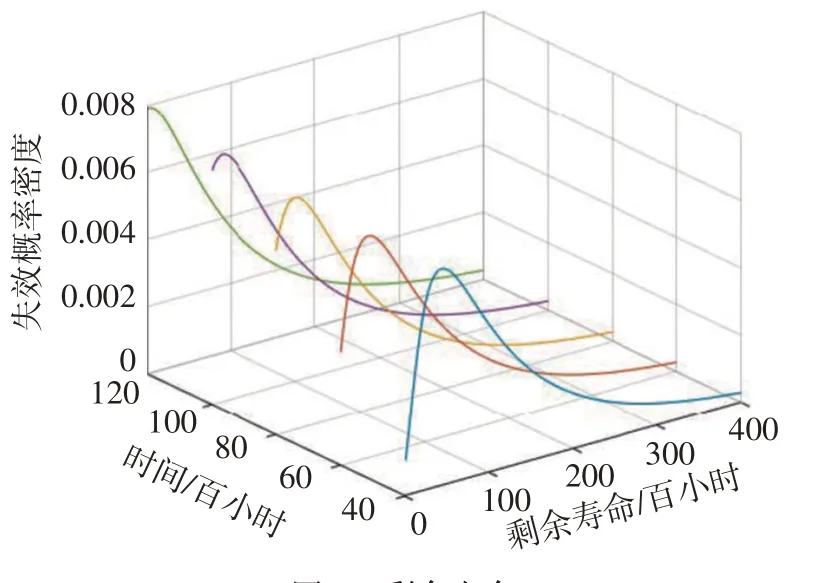
圖5 剩余壽命Fig.5 Residual life

從表4可以看出，隨著預測數據量的增加，預測誤差越來越小，到10 000 h以后，預測最準確，與4個樣本實際平均壽命26 350 h相比，壽命非常接近，誤差最小。表4 中的結果與圖3 中的可靠度時間25 000 h接近，因此可以看出Wiener 過程預測的穩定性和準確性。

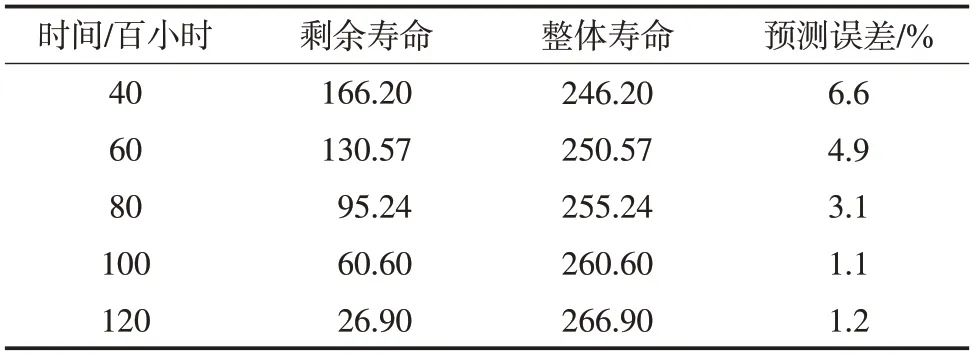
表4 基于Wiener 過程的壽命預測值Tab.4 Life prediction based on wiener process

為了進一步驗證方法的有效性，下面將Wiener過程剩余壽命所用的平均退化軌跡數據代入ARIMA模型對高壓閥的剩余壽命進行預測，對2個模型的壽命預測進行對比分析。

3.4.2 基于ARIMA 模型壽命預測

ARIMA 模型是一種針對非線性時間序列表現良好的預測方法[16]。高壓閥泄漏量退化數據具有動態、周期性、非線性特征，其退化機理復雜。ARIMA 模型只考慮單個變量，不以高壓閥復雜的失效機理作為依據，而是以高壓閥泄漏量的退化規律進行預測。

由圖2中高壓閥的平均退化軌跡可知，序列呈現出遞增趨勢并且存在較大波動性。為了讓序列不再表現出趨勢性，對退化量數據進行一階差分，詳見圖6。

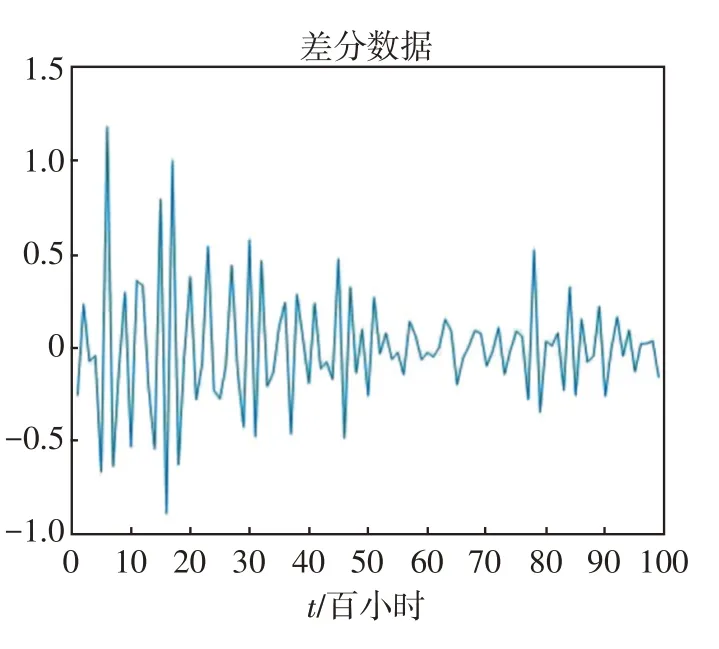
圖6 泄漏量的差分Fig.6 Difference in leakage

對退化量數據一階差分后，序列不再具備趨勢性，可考慮建立效應模型（p，d，q），由于實際建模時常用高階的ARIMA模型代替相應的移動平均模型MA和自回歸移動平均模型ARMA。樣本自相關系數和偏自相關系數顯然不為0，故p=q=1。因此，一階ARIMA模型為

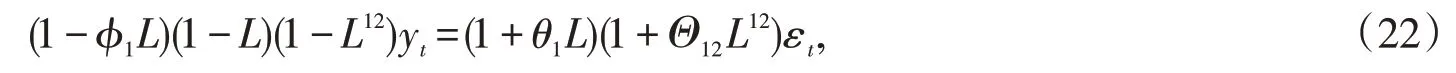
對所建立的模型進行擬合性檢驗，推斷殘差是否符合正態分布，如圖7所示。從圖7中可以看出，模型中的殘差滿足正態假設，說明ARIMA模型對高壓閥的剩余壽命擬合合適。

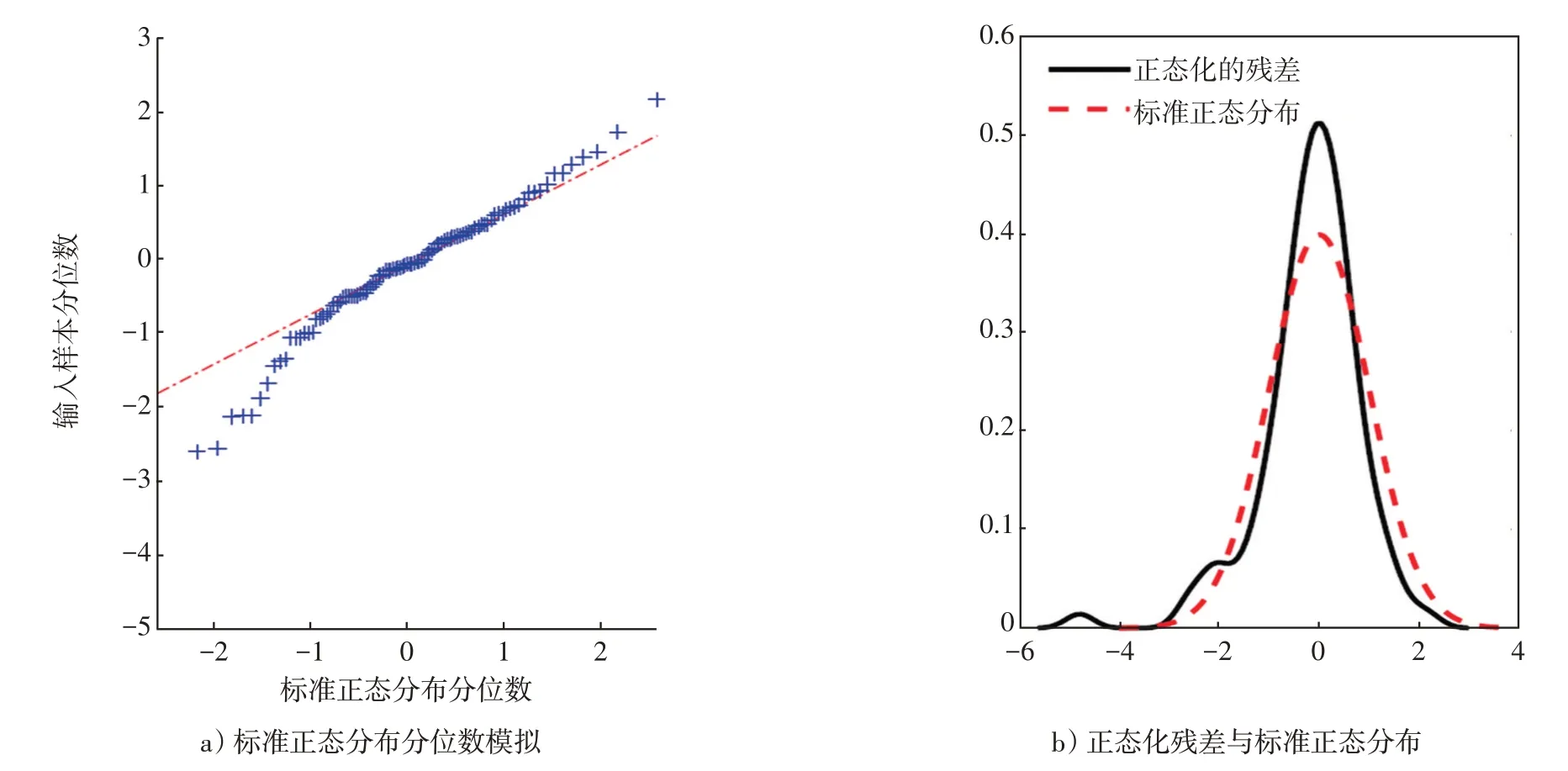
圖7 殘差的正態性檢驗Fig.7 Normality test of residuals

ARIMA時間序列模型所求得的剩余壽命如下表5所示，可以看出ARIMA模型不同數據量的壽命預測結果與實際平均壽命相比，誤差較大，預測不穩定。

根據表4 和表5，繪出Wiener 過程和時間序列的ARIMA 模型對高壓閥剩余壽命的預測值對比圖，如圖8 所示。從圖8 也可以看出，與試驗平均壽命相比，Wiener過程的預測結果更穩定，準確度更高。

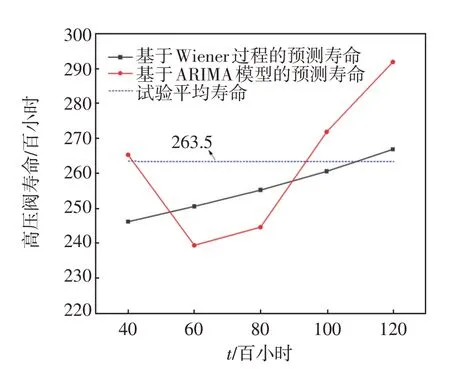
圖8 Wiener 過程和ARIMA 模型的預測壽命比較Fig.8 Comparison of the residual life of the wiener process and the time series method

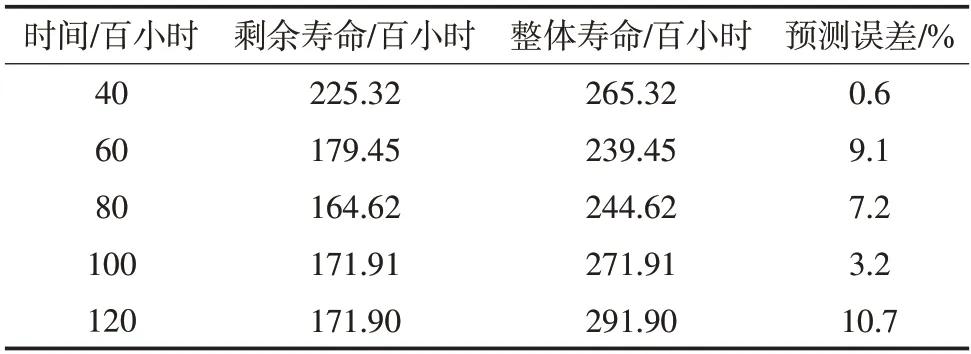
表5 基于ARIMA 模型的壽命預測值Tab.5 Life prediction based on ARIMA model

4 總結

本文結合高壓閥關鍵性能參數退化特點，提出了考慮個體差異的Wiener過程模型對泄漏量退化數據進行建模，用極大似然法對模型參數進行估計。該方法充分考慮了高壓閥由于一些外部原因產生的個體差異問題，可以提高壽命預測的精度。研究中選取了4 個高壓閥泄漏量的平均退化軌跡，求出失效概率密度函數、可靠度函數以及剩余壽命，采用ARIMA 模型根據平均退化軌跡進行剩余壽命預測分析的方法，驗證了基于個體差異的Wiener 退化模型預測的更加有效、準確。此模型可用來評估小樣本、高可靠、數據非線性、帶有波動性的產品，與ARIMA 模型預測結果相比，本模型預測更加準確。