基于解析初值的滑翔飛行器軌跡快速規劃方法

呂名添，周 祥，張洪波

(國防科技大學空天科學學院空天工程系，長沙 410073)

0 引言

小型滑翔飛行器是一種由飛機或助推器加速，在多種高度投放、進行亞/跨聲速飛行的無動力飛行器，具有體積小、發射時間短、使用靈活等特點。為保證小型滑翔飛行器能夠完成預定任務，快速生成一條滿足各類約束的參考軌跡至關重要。

根據是否對目標函數直接尋優，軌跡規劃方法分為直接法和間接法。由于直接法約束處理更靈活、問題適應性更強等優勢，近年來得到了廣泛研究和應用，其代表方法有偽譜法、凸優化等，本文主要關注偽譜法。偽譜法采用正交多項式的根作為離散點對狀態變量和控制變量同時離散，將軌跡優化問題轉化非線性規劃問題，再利用序列二次規劃(Sequential Quadratic Programming，SQP)等底層求解算法求解。SQP通過迭代求解一個二次規劃問題序列，使得迭代解逐步收斂至原問題的最優解。在首次構造迭代子問題時，必須借助初始軌跡近似處理約束和性能指標，以后的迭代則采用上一次的解構造新的子問題，直至滿足收斂條件。因此，初始軌跡會影響序列二次規劃算法的迭代子問題構造，進而影響偽譜法的收斂性和求解效率。

文獻中提出的初始軌跡生成方法包括線性假設法、智能算法等。周祥等提出利用線性假設法生成初始軌跡，對非凸的三維剖面規劃問題進行凸化處理，實現了序列凸化算法迭代求解原始非凸問題。孫志遠等針對火星進入軌跡規劃問題采用線性假設法生成初始軌跡，將其作為自適應偽譜法的輸入，實現了最優軌跡的快速生成。Kim等提出引導策略搜索方法，每次迭代采用序列凸規劃算法生成軌跡，再通過反饋控制律生成其他軌跡，所有軌跡共同用于更新神經網格策略，從而提高初始軌跡精度。Zhang等應用隨機快速搜索樹算法生成初始軌跡，減小隨機選擇點與預期點的距離，并將其作為高斯偽譜法的輸入從而得到最優軌跡。馬林設計了啟發式初始化策略，以基于低密度網格的軌跡優化問題最優解作為高密度網格軌跡規劃的初始軌跡，改進了非線性規劃問題的收斂性。Wu等提出了一種基于混合粒子群算法的初始軌跡生成方法，通過該算法在優化外循環中作用，生成有利于偽譜法收斂的初始軌跡。從已有結果來看，雖然線性假設法生成初始軌跡的效率較高，但存在精度較低、收斂性較差的問題；智能算法可以獲得接近最優解的初始軌跡，精度較高、收斂性好，但初始解生成的效率較低，從而降低了偽譜法的整體效率。因此，需要研究能在精度與效率間取得平衡、具備工程應用潛力的初始軌跡生成方法。

在一定的假設條件下，滑翔飛行器的運動方程存在解析解，能夠近似描述飛行器的運動特性。王肖等基于準平衡滑翔條件建立了航程與能量、傾側角的解析關系，從而得到航跡角和攻角解析解。曾亮基于一定假設，推導了速度、速度傾角、傾側角關于高度的解析解，有效提高了終端狀態的預測精度和效率。本文將解析解的研究思路拓展到軌跡規劃問題中，研究以飛行軌跡的近似解析解作為偽譜法迭代初值的方法，從而提高偽譜法的收斂速度和計算效率。

1 滑翔飛行器軌跡規劃問題建模

1.1 運動方程

考慮到小型滑翔飛行器的航程較短、高度跨度較小、速度較低等特點，提出以下幾點假設，作為運動學建模基礎：

1)假設地球為一圓球，半徑為其平均半徑；

2)略去地球自轉的影響，=0；

3)假設引力加速度受高度的影響可以忽略，設為常值=9.8 m/s；

4)飛行器以純空氣舵控制，認為飛行器的縱軸始終處于起滑點速度矢量與地心矢所在的平面內，側滑角=0。

結合上述假設，小型滑翔飛行器在半速度坐標系中的微分方程為

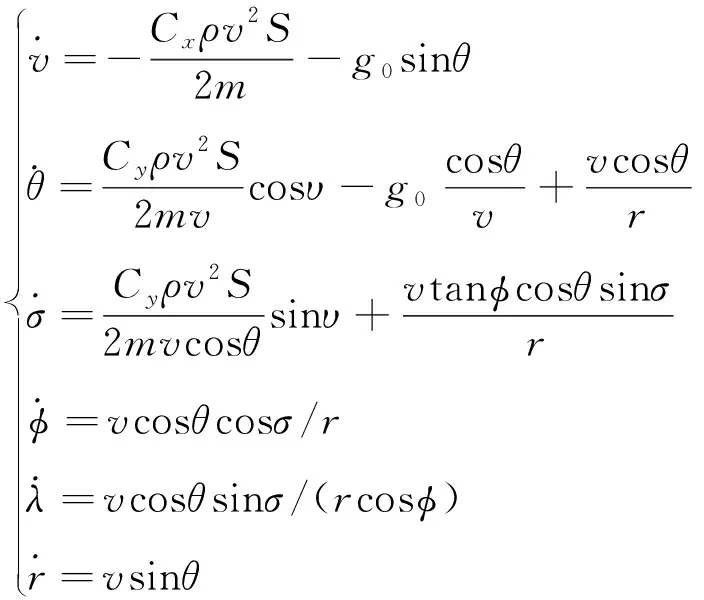
(1)

式中，為飛行器相對地球速度，為當地速度傾角，為航跡偏航角，規定順時針為正，為地心距，為經度，為緯度。為阻力系數，為升力系數，為氣動參考面積，為飛行器質量。

1.2 軌跡規劃問題描述

飛行器在半速度系的射程變化率為

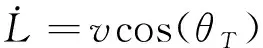
(2)

式中，為飛行過程中的速度傾角。

本文研究縱程最大，故構造目標函數為

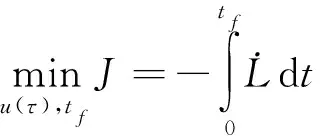
(3)

為滿足飛行器控制系統要求，考慮攻角、傾側角變化率約束，將原控制量擴維至狀態量中，在方程(1)的基礎上增加兩個微分方程

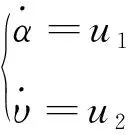
(4)

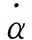
飛行器滑翔過程滿足動力學方程、邊界約束、過程約束等條件，以控制量、終端時間為優化變量，可將軌跡優化問題寫為以下形式

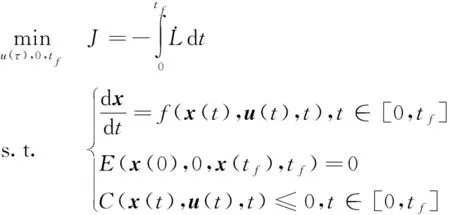
(5)

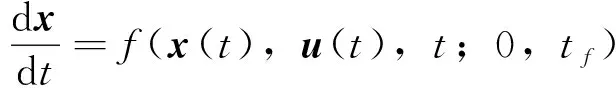
2 初始軌跡在偽譜法中的影響分析

偽譜法求解軌跡規劃問題的主要思路是將原問題轉化為非線性規劃問題，并通過序列二次規劃算法進行求解。初始軌跡主要用于首次構造二次規劃問題。

令={,}，={,，…,()}，，(=1,2，…,)分別為離散點處的狀態量和控制量，則非線性規劃問題可描述為

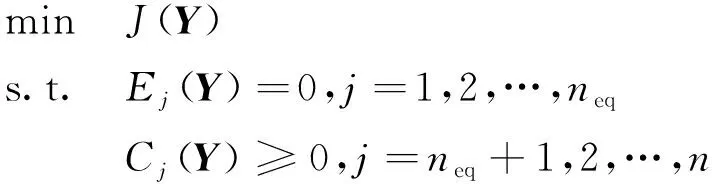
(6)

式中，為等式約束的個數，為所有約束個數。偽譜法處理原問題的過程可參考文獻[13-14]。

SQP算法是擬牛頓法解無約束問題的推廣，可用來求解上述非線性規劃問題，其基本思路是把式(6)所示的非線性問題轉為二次規劃(Quadratic Programming，QP)子問題，通過依次求解每個子問題得到下降方向，重復以上步驟直至滿足誤差容限，最終獲得規劃問題的最優解。

在每次迭代過程構造二次規劃問題

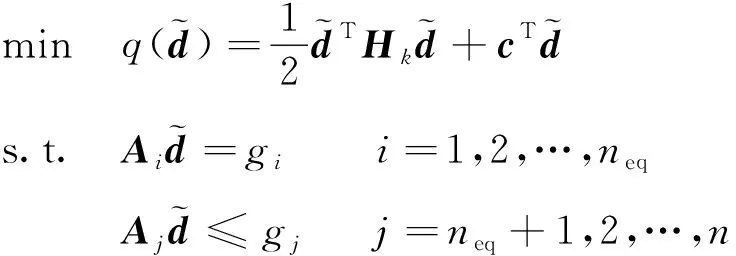
(7)

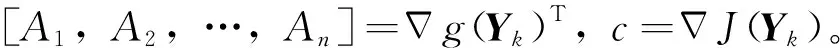
上述構造主要是將原始非線性動力學約束和過程約束在初始軌跡附近進行線性展開，得到式(7)所示的線性化矩陣。在完成首次QP問題構造后，求解該QP問題會得到一組新的迭代解，將該迭代解作為下一次迭代時求解矩陣的參考軌跡，從而啟動SQP算法。因此，初始軌跡對于后續序列二次規劃的收斂進程將產生影響，有必要研究一種能夠平衡精度與效率的初始軌跡生成方法。

初始軌跡在偽譜法求解軌跡規劃問題中的作用如圖1所示。

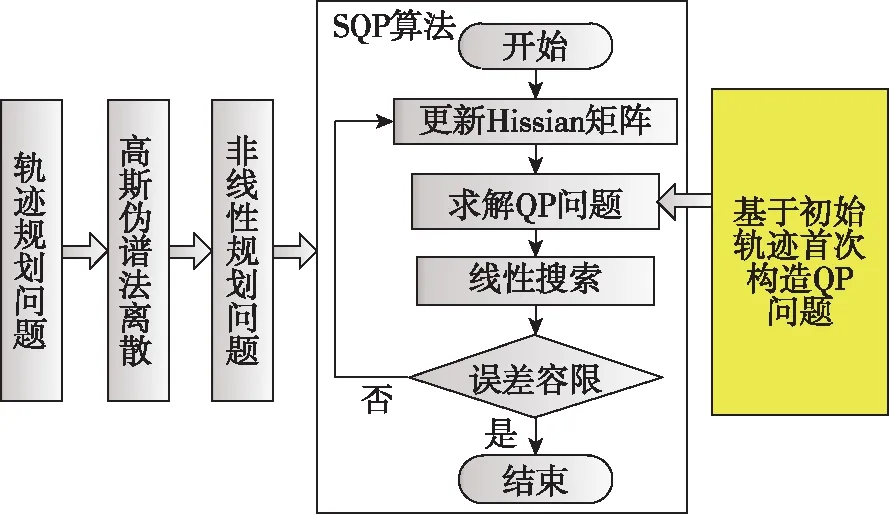
圖1 初始軌跡在軌跡規劃問題中的影響示意圖Fig.1 Schematic diagram of the influence of the initial trajectory in the trajectory planning problem

3 初始軌跡生成的解析解

小型滑翔飛行器動力學方程具有強非線性，控制量與狀態量相互耦合，直接推導解析解是非常困難的。本節在第1部分的微分方程基礎上做如下假設，推導用于生成初始軌跡的解析解：

1)準等溫大氣模型與實際大氣模型計算氣體參數比較接近，假設大氣密度模型為指數模型，即

()=-

(8)

式中，為標準大氣密度，為大氣密度參數,=1720 01 m；

2)采用常值攻角、傾側角剖面；

3)假設氣動模型在整個飛行過程為常值，不隨速度、攻角變化。

由圓球假設，地心距與高度的關系為

=+

(9)

由式(1)和式(9)得

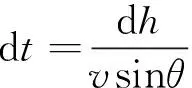
(10)

對當地速度傾角微分方程進行簡化

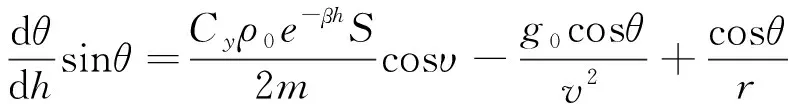
(11)

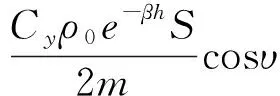
令=2，且設函數(,)為

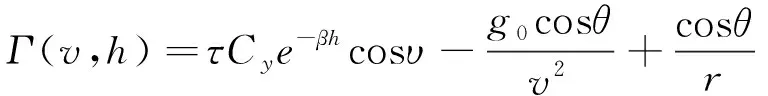
(12)

則式(11)等價于

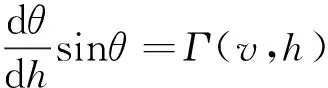
(13)

若(,)始終小于0，與呈正比，且釋放點處的當地速度傾角小于0，則整個滑翔過程的當地速度傾角都將小于0，從而保證飛行器高度單調下降。

方程(11)右端3項經過數值計算，發現氣動升力項遠大于引力項與附加力項，根據式(12)中氣動升力項的表達式，通過設計傾側角幅值，可構造函數(,)為

(,)=--

(14)

在上式構造的函數中，由于大氣密度參數與指數函數恒正，則參數的符號決定了函數(,)的正負。若參數取正值，則飛行器的高度在滑行飛行段將單調下降。

結合式(13)和(14)，可得到當地速度傾角的解析表達式為

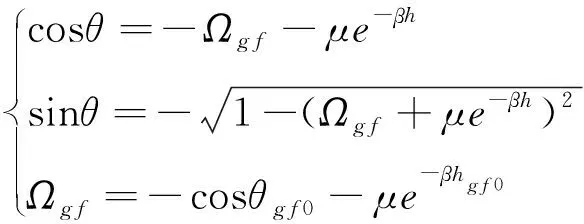
(15)

式中，為滿足初始狀態的積分常數，0和0分別為釋放點處的當地速度傾角和高度。

同理，推導速度關于高度的解析解，結合式(1)和式(10)，對速度微分方程簡化得到

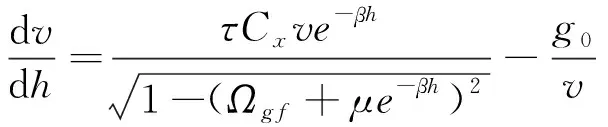
(16)

式(16)中由于引力項與氣動升力項量級相當，難以略去，因此速度大小不能獲得解析解，只能得到上述半解析解。

至此，利用上述解析解實現初始軌跡生成的流程如下：

1)根據初始高度和終端高度確定離散點個數，給出高度下降曲線；

2)利用式(15)計算速度傾角關于高度的解析變化曲線；

3)利用Runge-Kutta積分方法計算方程(16)，得到速度關于高度的變化規律；

4)假設其他狀態量及控制量為常值，得到完整的初始軌跡。

4 仿真分析

4.1 仿真條件

本節利用所提解析初值進行小型滑翔飛行器軌跡快速規劃，對解析方法的有效性進行仿真驗證。調用MATLAB平臺下的IPOPT求解器對軌跡規劃問題進行求解，相對誤差精度設為1×10。飛行器質量為200 kg，參考面積為0.1 m，升阻比為2左右。初始任務參數為：=3，=-1°，=90°，=25 km，=0°，=0°。

在初始高度與終端高度之間均勻確定250個離散點，根據所提解析方法獲得速度與速度傾角在每個高度處的大小，航跡偏航角、經緯度、傾側角均設為常值0°，攻角設為常值15°，至此可得到完整的初始軌跡，序列二次規劃算法可以啟動。

4.2 仿真結果

基于偽譜法軌跡規劃得到的控制量，以四階Runge-Kutta積分結果作為最優軌跡精確值，驗證所提解析方法的可行性。圖2～5給出了解析解作初始軌跡對應的狀態量變化曲線，藍色實線是偽譜法規劃結果，紅色短線是Runge-Kutta積分精確結果，綠色虛線為解析方法計算的初始軌跡。

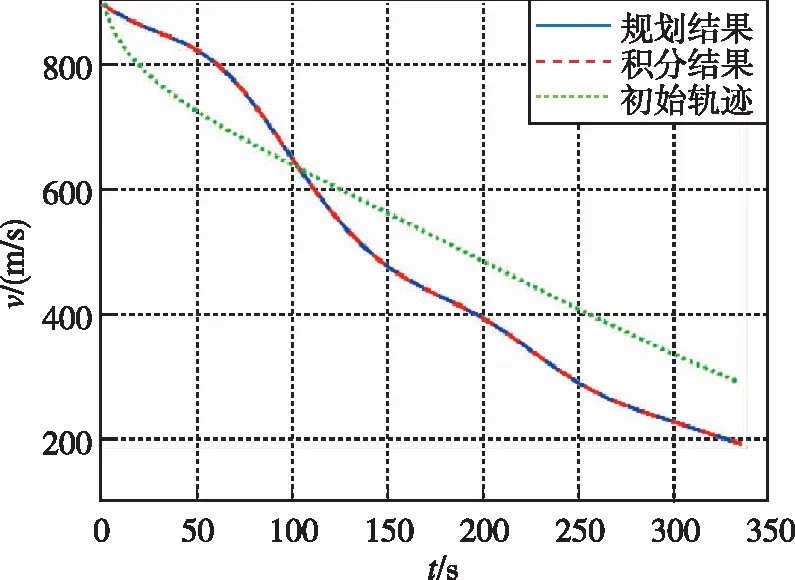
圖2 速度變化曲線Fig.2 Speed curve

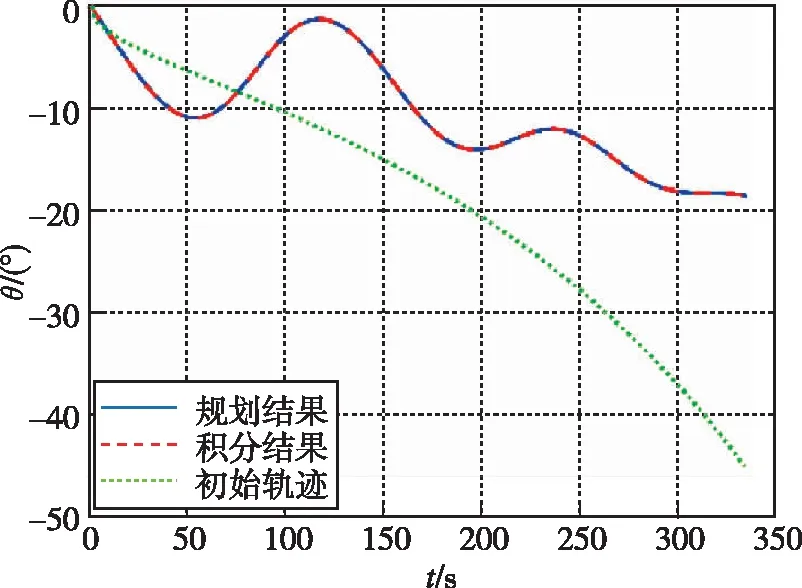
圖3 速度傾角變化曲線Fig.3 Velocity inclination curve

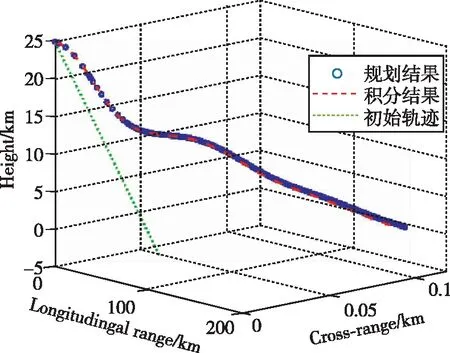
圖4 規劃與積分軌跡三維圖Fig.4 3D plot of planning and integrating trajectories

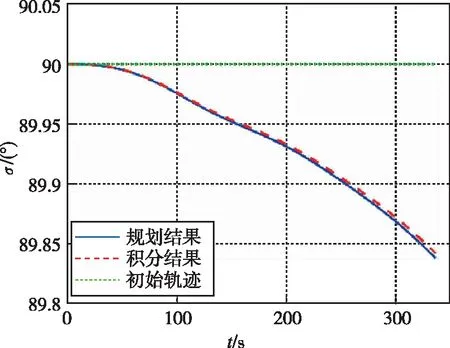
圖5 航跡偏航角變化曲線Fig.5 Track angle curve

由圖2～4中的規劃解與積分解可以看出，速度傾角全程小于0°，終端高度滿足邊界約束，速度、高度呈三段式持續減小，說明飛行前期、后期升力較小，不滿足平衡滑翔條件，而飛行中期，大氣密度、速度在一個合適范圍內，升力大于重力。圖4、圖5中，規劃解的航跡偏航角變化小于0.5°，飛行器側向機動范圍較小，軌跡整體沿正東方向從而得到初始飛行能力下的最大縱程。規劃結果與積分結果航程為166.48 km，終端狀態量偏差較小，說明優化解的狀態量與控制量基本滿足動力學約束，軌跡規劃方法是正確的。對比初始軌跡與規劃結果，雖然解析解與規劃軌跡相差較遠，但偽譜法仍能找到滿足迭代精度的可行解，說明偽譜法對初始軌跡具有較好的適應性，能夠確保方法自身收斂。

從圖6、圖7可以看出，控制量全程滿足幅值約束與角速率約束，對控制執行機構產生的壓力較小。

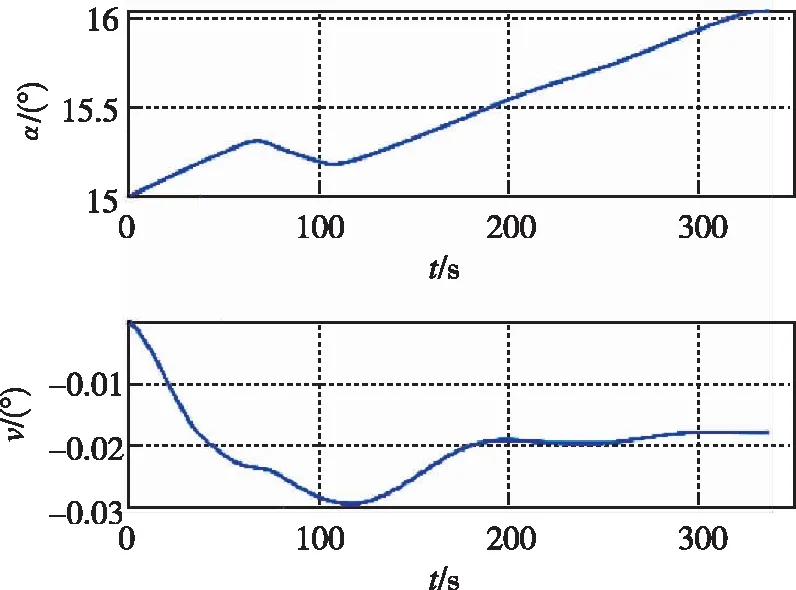
圖6 攻角和傾側角變化曲線Fig.6 Variation curve of attack angle and bank angle

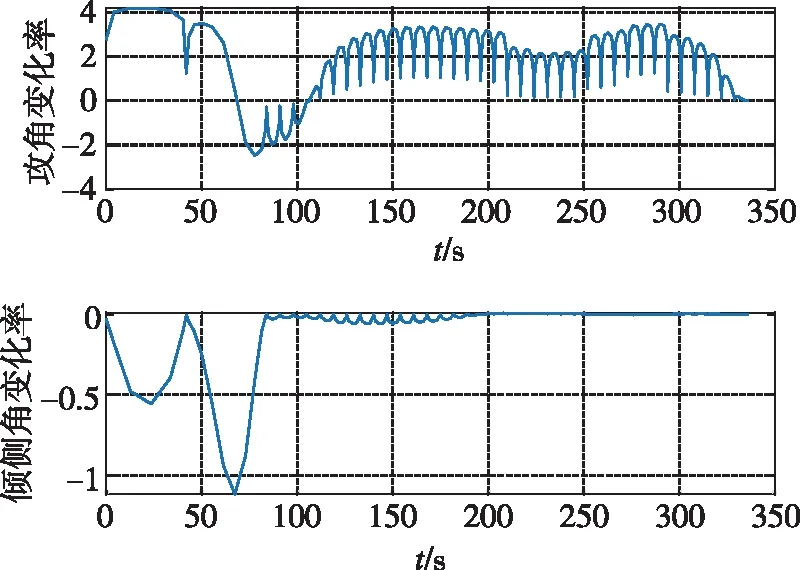
圖7 攻角和傾側角變化率曲線Fig.7 Variation rate curve of attack angle and bank angle

在偽譜法初始軌跡生成中，常用線性假設和簡化數值積分兩種方法，其中線性假設法是以初始狀態、終端狀態為端點的線性變化曲線作初始軌跡，簡化數值積分則是假定控制量為常值，通過數值積分得到初始軌跡。

表1給出了3種初始軌跡進行軌跡規劃所得收斂情況的對比結果。CPU時間是指調用IPOPT求解器所用時間，總規劃時間為初始軌跡生成時間與CPU時間之和，迭代次數是指相對誤差滿足網格細化精度的迭代次數，間隔數是指網格細化分段內的間隔數目。

由表1可以看出，3種方法實際計算精度均小于誤差容限1×10，得到精度較高的收斂解；解析方法與簡化數值積分法需要大約1.68 s，迭代21次得到最優軌跡；解析方法總規劃時間最短。

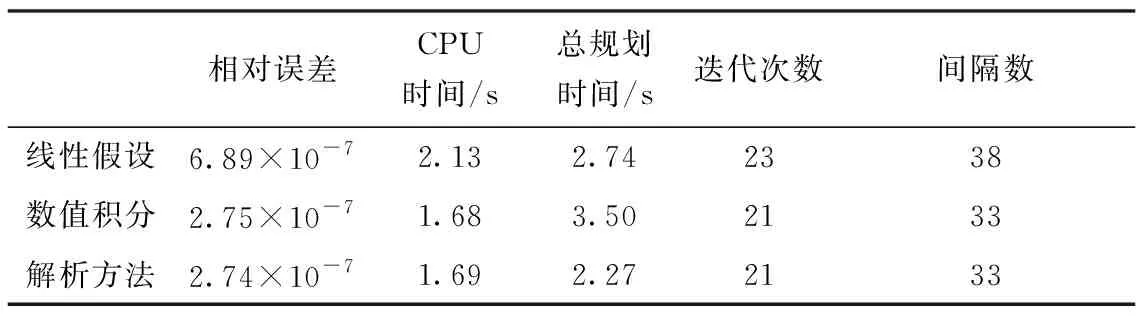
表1 不同初始軌跡生成方法對應的收斂結果Tab.1 Convergence results corresponding to different initial trajectory generation methods

分析表1所示結果，主要原因在于初始軌跡的精度和與最優解的距離。線性假設生成的初始軌跡不滿足動力學約束，精度較低，且與最優解距離較大，所以將其作為初始軌跡使得偽譜法迭代次數較多。簡化數值積分生成的初始軌跡嚴格滿足動力學約束，精度較高，解析方法生成的初始軌跡在簡化條件下滿足動力學約束，精度略低，因此這兩種方法的收斂迭代次數與CPU時間基本一致，計算精度、求解效率均優于線性假設法。

總規劃時間不同是因為生成初始軌跡的時間不同，簡化數值積分法需對8個狀態量數值積分才能獲得初始軌跡，而本文所提解析方法僅需對速度一項進行積分，速度傾角通過解析公式計算，其他量通過常值確定，所以計算量小于數值積分法。因此，可認為本文所提解析法是一種平衡了初始軌跡生成效率與求解精度的較好方法。

5 結論

本文針對傳統初始軌跡生成方法難以兼顧效率與精度的問題，以小型滑翔飛行器為對象，提出了一種基于解析初值的軌跡快速規劃方法。首先基于一定假設建立了簡化的運動學微分方程，其次分析了初始軌跡對偽譜法收斂性的影響過程，最后推導了速度傾角、速度關于高度的解析/半解析解。仿真中，相比線性假設法，解析方法能夠提升偽譜法的收斂迭代精度和計算效率；相比常值積分法，解析方法生成初始軌跡的計算量小且求解精度、效率與其相當。因此，解析初值平衡了初始軌跡生成效率與求解精度，基于該解析初值的軌跡規劃方法具備較強的工程適用潛力。