基于類內類間距離量級平衡的FCM聚類算法設計

江文奇, 牟華偉

(南京理工大學 經濟管理學院,江蘇 南京 210094)

0 引言

網絡環境下數據與數據處理能力已經成為互聯網企業的重要競爭力。近年來，第三方電子商務平臺收集并存儲了大量的客戶購物和評價信息，通過實施客戶聚類有效表征了不同類別客戶的特征偏好，為精準營銷提供了有力支撐。

聚類本質是將大量數據從空間上進行一種無監督無標號的劃分，目的是挖掘數據的內在聯系和潛在價值，已經廣泛應用于模式識別、機器學習等領域[1]。模糊C均值(Fuzzy C-means, FCM)算法是一種常見且廣泛應用的聚類算法，魯棒性好且收斂性強。其中，初始聚類中心點、每個數據點與聚類中心點的隸屬度、聚類模型設計等是FCM算法的核心內容[2]。

現有FCM聚類算法研究均突出了聚類穩定性特征。如文獻[3]引入多維數據的鄰域信息改進聚類算法，增加異常值和噪聲點的穩健性。文獻[4]根據數據之間互為K近鄰關系來確定數據中的自然簇，減少算法對聚類參數的依賴程度。文獻[5]提出基于全部最小連通支配集的聚類算法解決了算法易于陷入局部最小值的缺陷。多維大數據環境下，文獻[6]結合灰狼算法和最大熵理論刪減屬性；文獻[7]采用折線模糊數描述待聚類對象的指標信息并設計聚類算法；文獻[8]提出了一種自適應特征熵權的FCM算法分析屬性權重對聚類算法的影響程度；文獻[9]將偏好矢量相聚度作為鄰域相似度，構建啟發式聚類算法解決多屬性復雜大群體聚類與決策問題。

上述文獻注重FCM算法的穩定性問題，但忽視了FCM目標函數對于聚類績效的影響。通常，聚類模型與算法設計的有效性部分受制于目標函數，而目標函數中類內類間距離合成形式是關鍵點。于是，本文擬深入分析類內距離和類間距離之間的關系，基于兩類距離數值量級的差異性，設計兩類距離平衡方法，進而提出一種新的FCM聚類目標函數設計和聚類算法，提高多維大數據環境下FCM算法的聚類績效。

1 FCM聚類算法概述

FCM聚類算法是一種應用廣泛的聚類算法，其原理是基于數據屬性的相似性以及數據屬性的差異性，通過自動迭代算法實現對大量數據的聚類劃分。假定聚類數據量為n(X=(x1,x2,…,xn)∈RS)，數據集維度為s，聚類中心點數為c，vi為第個聚類中心點，uij為樣本點j對第i個類的隸屬度(隸屬度矩陣為U)，dij為樣本點j對第i個聚類中心點的距離，模糊加權數m∈[1,∞)。經典FCM算法的優化模型為:

(1)

運用Lagrange乘子法求解，有:

(2)

其中，1≤i≤c,1≤j≤n。

FCM算法具體步驟描述為:

首先：確定聚類中心點個數c，模糊權重值m，初始聚類中心點vi。給定判斷兩次目標函數值大小之差或者目標函數迭代終止閾值β。

其次：依據式(2)求隸屬度矩陣和新的聚類中心點，由式(1)求得目標函數值。

最后：計算前后兩次目標函數值之差與β的大小關系(或目標函數值與β的大小關系)。若兩次目標函數之值小于β值，則輸出聚類中心點和隸屬度矩陣，否則，重復步驟(2)。

2 FCM中類內與類間距離關系研究

針對經典的FCM聚類模型，以SFA和SFE跡表示類內和類間距離，有:

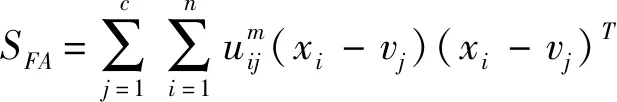
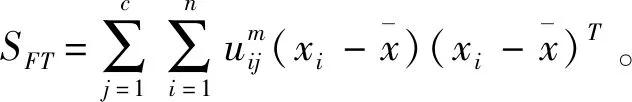
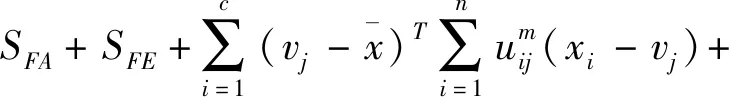
tr(SFT)=tr(SFA)+tr(SFE)

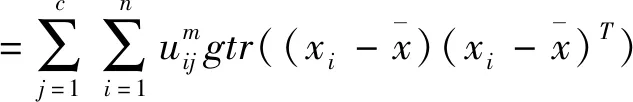
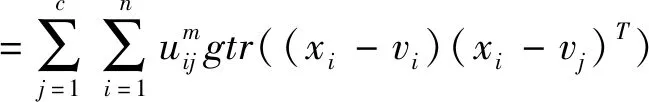
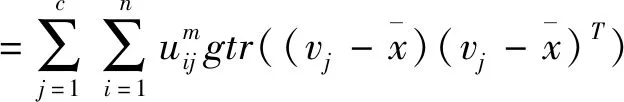
其中：tr(SFA)是經典FCM目標函數JFCM，tr(SFE)可作為具有隸屬度加權類間距離測度，tr(SFF)為僅依賴于隸屬度的不確定值。

為了平衡FCM聚類算法的類內類間距離，實現聚類過程中類內類間距離的有效融合，當前FCM聚類算法模型優化主要有以下幾種方式：(1)添加懲罰函數項，動態調整類內類間距離差距；(2)增加權重系數平衡類類內類間距離；(3)結合熵函數表征類間離散程度、(4)基于核函數改變類內類間距離度量方式。結合tr(SFT)表達式，分析FCM聚類目標函數的類內類間距離關系。

(1)文獻[10]結合競爭學習思想，在目標函數中添加懲罰函數項，目標函數表示為:

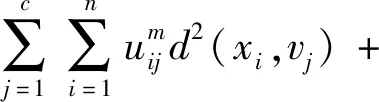
懲罰函數項為:

在tr(SFT)=tr(SFA)+tr(SFE)兩側添加加懲罰函數項可得:

等式右端為文獻[10]類內距離目標函數值和類間距離之和，左側值:

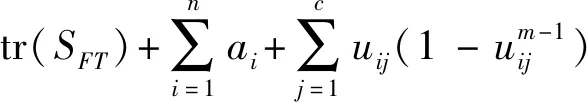
J(U,V)+tr(SFE)受到隸屬度函數以及ai影響，不能確定min(tr(SFA))與max(tr(SFE))變化的一致性，即在確定類內距離最小化的同時不能保證類間距離最大化。

(2)文獻[11]基于群體排斥思路添加懲罰項改進FCM聚類算法，目標函數為:

tr(SFT)=tr(SFA)+tr(SFE)左右加懲罰項，有:

等式右端為類內距離優化與類間分離度的和，左側值：

因此算法沒能有效實現類內距離最小化與類間距離最大化的融合。

文獻[10,11]設置隸屬度函數作為懲罰項，雖然降低了總體離差tr(SFT)對uij依賴程度，但沒有實現JFCM最小化時tr(SFE)最大化有效融合。

(3)文獻[12]基于高斯函數設置距離測度，并增加懲罰項以解決類內類間距離的融合問題。

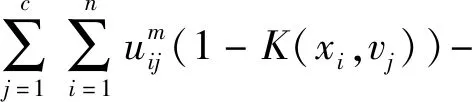
目標函數改進了tr(SFE)，對某樣本點有:

若保證0≤uij≤1，則必有:

使得類間距離收縮到(0,1)范圍內，在量級上與類內距離差距較大，不利于實現不同類的劃分。

(4)文獻[6]在兼顧類內距離與類間距離的基礎上，提出改進型距離測度，其目標函數為:

文獻[12,6]基于min(tr(SFA)-tr(SFE))思想，融合類內類間距離，理論上能夠實現類內緊湊度與類間分離度同步最優化，但不同量級的類內類間距離差異大，會導致聚類效果不佳。

(5)文獻[13]在目標函數中引入了聚類中心距離懲罰項，將類間距離分離度融合到目標函數，有:

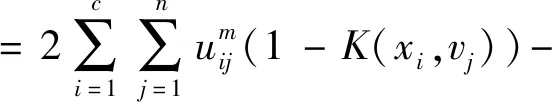
(6)文獻[14]在目標函數中增添了最大中心間隔項與縮放因子η，避免了聚類中心趨于一致性。

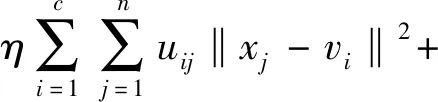
雖然文獻[13,14]在類內類間融合上提出了創新算法，但沒有有效解決類內類間距離的差異性對FCM聚類的影響。

上述類內與類間距離融合優化并不能有效實現類內距離最小化與類間距離最大化一致性變化，即聚類算法實現類內距離最小化的迭代過程，類間距離不能同步實現最大化。

3 FCM改進聚類算法設計

為了解決FCM聚類目標函數中類內距離和類間距離合成難的問題，實現類內距離最小化且類間距離最大化的聚類目標，本文將基于min(tr(SFA)-tr(SFE))的思想來設計FCM目標函數，借助高斯核函數距離測度改進目標函數相似性函數，統一類內類間距離的合成基礎。

類內距離和類間距離的差異可以表示為:

tr(SFA)-tr(SFE)=JFCM-tr(SFE)

采用高斯核函數將特征空間X映射到H來替代歐式距離，又K(x,x)=1，映射過程為:

d(x,y)=‖Φ(x)-Φ(y)‖2

=(K(x,x)+K(y,y)-2gK(x,y))

=2(1-K(x,y))

高斯核函數對類內類間距離進行改進:

為了更好體現類內距離與類間距離在目標函數中的影響，實現類內類間距離的有效比較，K(x,y)為exp(-‖x-y‖2)/σ2)，0≤K(x,y)≤1。基于高斯核函數的距離測度，d(xi,vj)∈(0,2)，d(vj,vk)∈(0,2)，保證了類內與類間距離在距離范圍上的一致性，提供了類內與類間距離融合的基礎。

對類內與類間距離融合作如下設計：

改進的類內類間融合公式保證了類內與類間距離非負性且值在區間(-2+2θ,2+2θ)內，θ∈(0,1)為調控因子，平衡了類內與類間距離的量級，確保了算法收斂性，區間上限提高了聚類算法的精確度。

令m控制分類的模糊程度，值越大表明模糊程度越高，σ2是給定數據方差。改進型FCM聚類模型表示為:

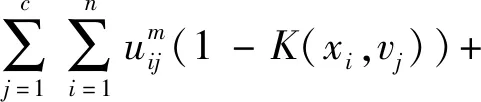
(3)

利用拉格朗日乘子法建立無約束優化目標函數:

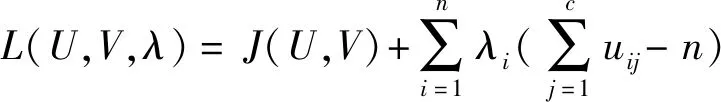
(4)

(5)

(6)

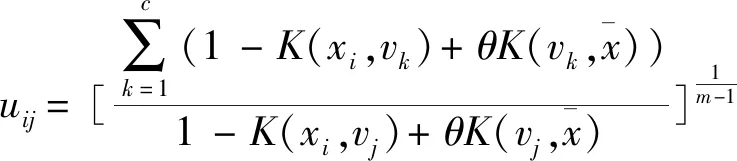
(7)

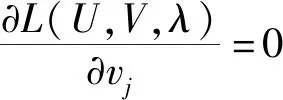
(8)

于是，改進的FCM聚類算法步驟表示為：

步驟1設定聚類個數、選取合適初始聚類中心點、模糊參數m、核函數參數σ、收斂精度ε、調控因子初始化為1/c、初始化迭代次數k=0；

步驟2依據式(5)計算各代表點隸屬度uij；

步驟3根據式(8)計算vj，令k=k+1；

步驟4若‖Uk+1-Uk‖≤ε，停止迭代，否則轉到步驟2；

步驟5輸出隸屬度矩陣U，聚類中心矩陣V。

4 算例研究

某企業為了設計針對學生人群的產品營銷計劃，選取了價格滿意度、服務水平、物流速度三個評價指標，隨機調查了南京地區600名學生客戶(通過問卷星發放并收集問卷，本文作者負責設計與分析問卷)，通過實施客戶聚類實現精準營銷。取m=2，θ=0.02，σ2=6，迭代終止條件cpsm=10-6。聚類中心點矩陣為:

圖1展示了本文提出的改進型FCM聚類算法的收斂過程，算法在5次迭代計算后開始收斂。圖2為算法收斂后所有樣本點的隸屬度值，表現了樣本數據點對每一類的歸屬程度。

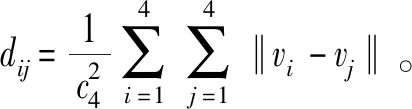
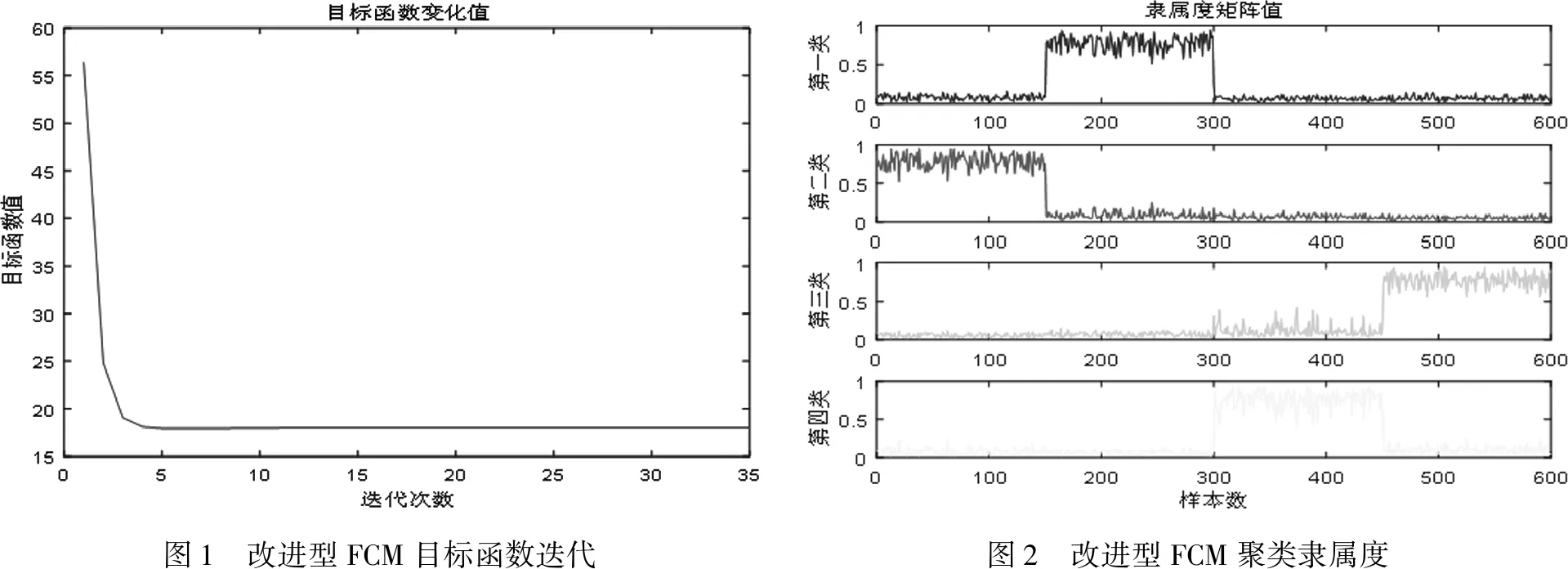
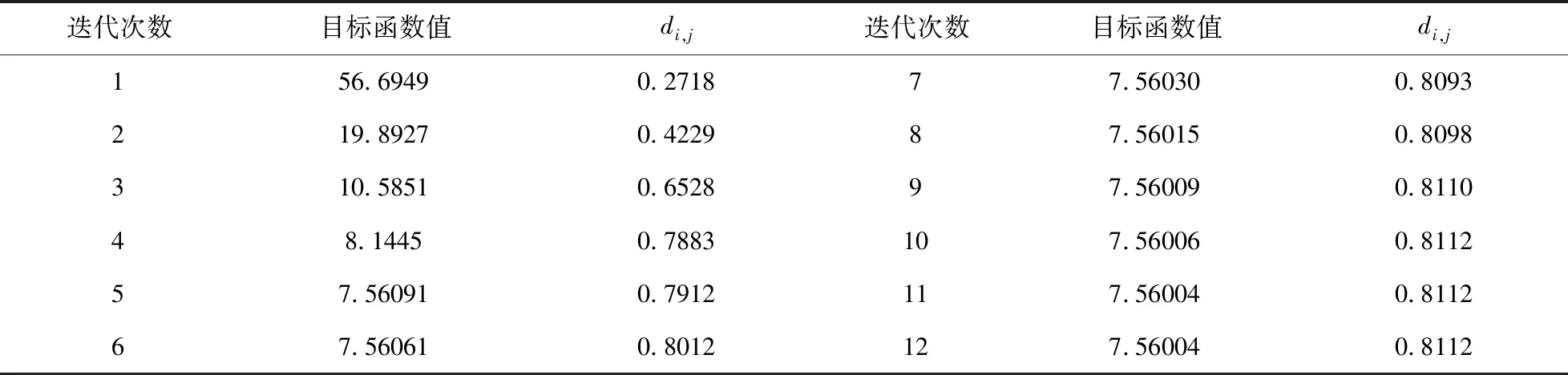
表1 改進型FCM類間距離變化

采用經典FCM算法進行樣本點聚類時，取模糊參數m=2，epsm=10-6，聚類中心點矩陣為:

經典FCM算法9次迭代后開始收斂，收斂曲線如圖3所示。圖4為經典算法迭代收斂后所有樣本點的隸屬度值。

經典FCM聚類目標函數與類間距離變化值如表2。

比較圖1和圖4收斂曲線：改進型FCM聚類算法5次迭代計算便開始收斂，經典的FCM算法在第8次迭代計算才開始收斂，改進型FCM算法能夠以更少的迭代次數實現算法的收斂，同時改進型FCM聚類算法的收斂曲線更加平滑，算法的穩定度更高。

通過對表1數據分析，隨著改進型FCM聚類算法目標函數值的減小，類間距離di,j不斷地增大，在目標函數值最小時類間距離達到最大。表2數據顯示，經典FCM聚類算法在前5次迭代過程中，類間距離di,j不斷增大，第5次迭代后，di,j隨著目標函數值的變小呈現出先增大后減小的趨勢，第8次迭代類間距離達到最大值，而目標函數值并未達到最小值，說明改進型聚類算法能夠有效的實現類內距離最小化與類間距離最大化的一致性變化。

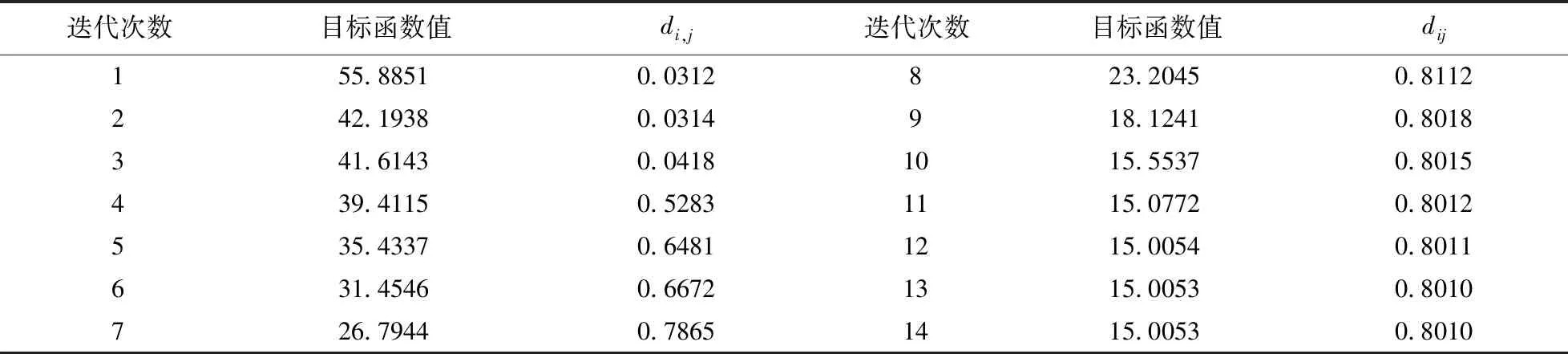
表2 經典FCM類間距離變化

為了進一步驗證本文提出的改進算法可行性和有效性，采用國際上的標準測試數據UCI標準數據集Iris、Wine、Glass樣本數據。

由表3可知，在維度方面Wine>Glass>Iris，分類方面則Glass>Wine=Iris。綜合分類以及量級差異性程度，Glass>Wine>Iris。

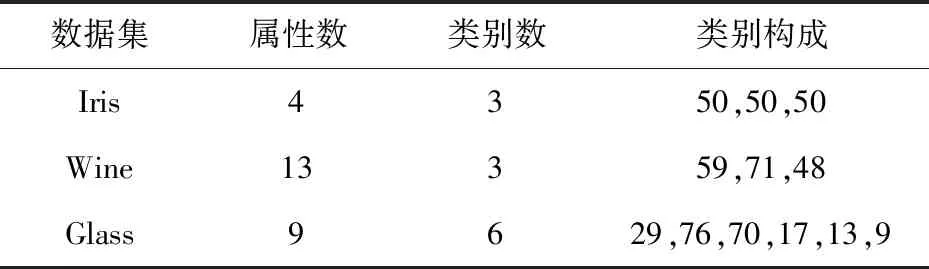
表3 實驗數據集

采用Windows7，Matlab編程環境，分別以經典FCM聚類算法、KFCM聚類算法、本文提出改進FCM算法流程對三類數據進行聚類效果統計。得到表4。

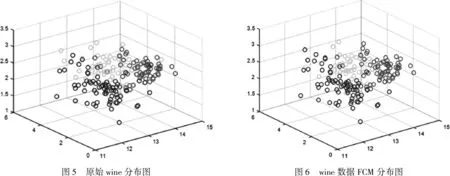
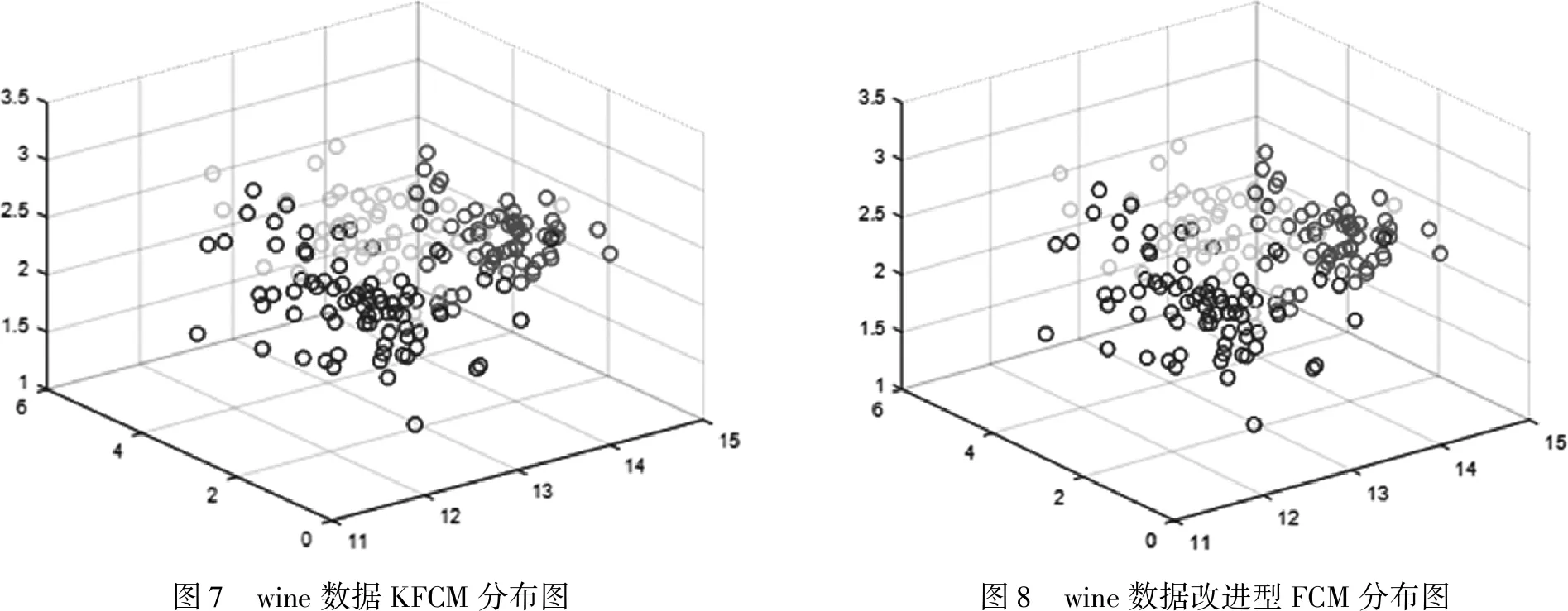
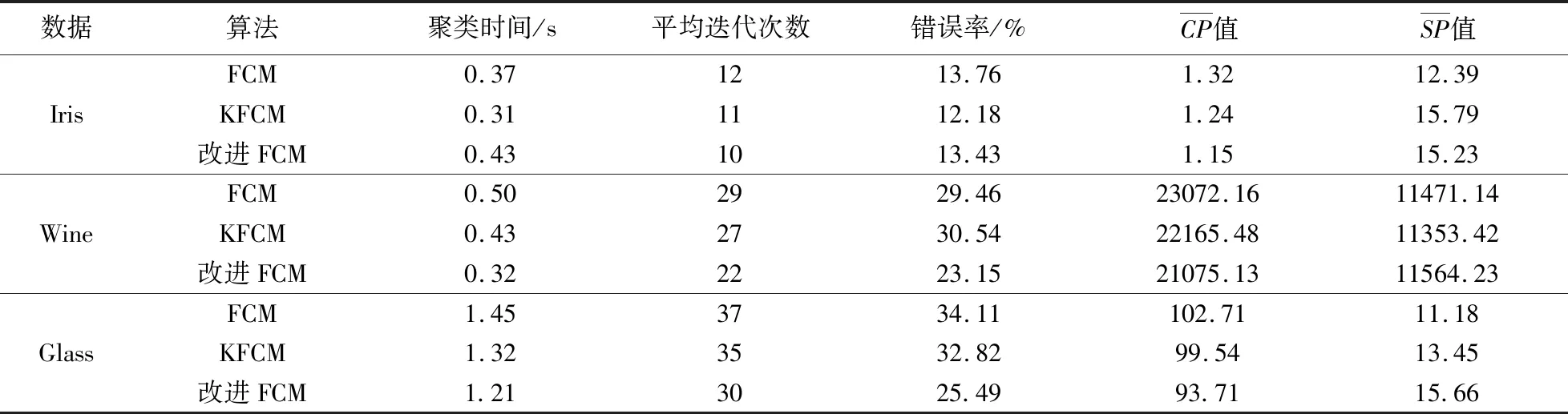
表4 聚類算法迭代效果

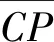
Compactness(緊密性)(CP):

Separation(間隔性)(SP)：

由上表可知在Iris數據集中，本文提出算法較其他算法處于平均水平，沒有較為明顯的優勢；分類數不變，量級出現偏差的高維數據集中，改進算法在除聚類時間外的聚類效果表現中有一定的優勢；而在量級差異較大且類簇更多的Glass數據總體來看，本文提出的改進算法平均迭代次數相比于其他的算法在逐漸減小，說明隨著數據量級的差異變大以及類內類間距離的差異性增加，本文改進算法能夠提高聚類效率。

算法計算時間方面，改進型聚類算法的時間復雜度為o(nkc)，與KFCM以及經典FCM算法相同。實際耗費時間上，對量級差異性不大的數據集，改進型FCM的算法復雜導致效率不高，耗時較長，但是對量級差異較大的數據集，改進行算法的迭代次數減少，時間降低。

結合改進型算法的聚類結果，類與類間的區別更為明顯，可將調查學生群體劃分為四類，即高消費人群、中等消費人群、服務主導型人群、普通型消費人群。針對不同的消費人群制定針對性的營銷策略，例如，可以對高消費人群推送奢侈商品廣告，對服務主導型人群可以推送服務型、提高生活質量的商品廣告。

5 結論

不同量級數據聚類中聚類數據點的數量巨大，易造成聚類過程類內與類間距離的影響差異較大的缺陷，從而導致FCM聚類算法不敏感。針對聚類過程中目標函數沒有有效地平衡類內與類間距離的問題，本文首先基于矩陣分解方式對類內與類間距離的關系進行分析，基于高斯核函數對類內與類間距離進行了融合，平衡類內與類間的影響。算例表明，改進的FCM聚類算法在處理大數據集的聚類過程中具有很好的收斂性以及魯棒性，但在處理小數據量以及類間距離效果不明顯，適用于處理類內與類間距離差較大的情況。