粘聲介質動態聚焦束逆時偏移

肖建恩, 白英哲, 李 博, 萬城程, 李仲庚

(1.中國石化 石油物探技術研究院，南京 211103;2.中國石化 河南油田分公司 勘探開發研究院，鄭州 450000;3.青島市海產博物館，青島 266000)

0 引言

地震偏移成像是地震勘探的關鍵環節之一，其主要目標是實現反射波的準確歸位和恢復反射界面的反射系數、振幅變化以及波場特征。大量研究表明，地下介質中粘滯性廣泛存在，采用各向同性成像算法來處理這些探區的數據，會導致成像位置不準確，成像振幅欠估計和分辨率降低等問題。因此，研究基于粘滯性的成像算法，對于獲得高精度地震剖面具有重要意義。

疊前成像算法依據理論不同可以分為：①射線類偏移;②波動方程類偏移。射線類偏移基于幾何射線理論來計算波場的走時、振幅等信息，進而實現波場延拓成像，靈活性和計算效率比較高。Krichhoff偏移是業界廣泛應用的射線類成像算法，主要通過波動方程積分解來進行波場的反向延拓和成像，不僅具有面向目標成像能力，而且對復雜觀測系統具有很好的適用性[1-3]。然而其依賴常規射線追蹤方法來求取旅行時，存在焦散區、陰影區和多次波至問題。作為積分類偏移算法的改進，高斯束偏移不僅能夠處理多次波至的問題，而且對低信噪比數據適用性更好。高斯束偏移算法采用彼此獨立的射線束來表征地震波場，不僅繼承了射線類偏移的靈活性和高效性，而且包含了波場的動力學信息，易于向各向異性、粘滯性和起伏地表等情況推廣[4-6]。

波動方程類偏移通過求解地震波場傳播過程中的傳播算子，進而采用遞歸算法來實現偏移成像，不僅能夠避免速度劇烈變化引起的焦散問題，而且能夠處理多值走時的情況。其依據方程不同主要分為：①單程波偏移;②逆時偏移。單程波偏移通過解耦之后的單程波方程來獲取延拓算子，并在此基礎上進行延拓，最后采用合適的成像條件進行成像[7-8]。相比射線類偏移，單程波偏移有更高的成像精度，然而其計算效率相對較低，不僅不能進行真振幅成像，而且無法處理陡傾構造成像問題。逆時偏移則是將地表接收到的地震記錄進行逆時延拓，進而和震源處正向傳播波場進行互相關來求取成像值，不受成像角度的限制，然而其不僅計算量巨大，而且對速度場的精確性要求較高，在實用化方面還有一定的局限性[9-11]。

在Kirchhoff積分的基礎上，Popov等[12]提出了采用高斯束加權積分來構建格林函數的逆時偏移算法，能夠面向目標成像；黃建平等[13]結合Popov的思想，采用高斯束表征的格林函數來實現地震波場正反向延拓，進而通過互相關成像條件來求取成像值，實現了格林函數高斯束逆時偏移方法。針對地下介質中廣泛存在的各向異性，張凱等[14]將彈性參數表征的各向異性射線追蹤算法應用于高斯束逆時偏移，實現了角度域各向異性高斯束逆時偏移方法，然而該方法不僅計算效率比較低，同時需要確定地下介質的彈性參數。針對上述問題，肖建恩等[15-16]研究了基于相速度的各向異性聲波和轉換波高斯束逆時偏移算法，進一步提升了算法的計算效率和適用性。

1 基本原理

各向異性動態聚焦束逆時偏移的實現與高斯束逆時偏移類似，主要包括動態聚焦束算子的構建、格林函數的加權表征、互相關成像以及粘滯性的校正等。

1.1 格林函數的動態聚焦束表征

圖1為二維中心射線坐標系，由初始點O(s0,0)到點R(sp,0)的傳播矩陣為式(1)。

(1)

由互易原理可知，從點R(sp,0)到初始點O(s0,0)的傳播矩陣可以表示為式(2)。

∏(sp,s0)=∏-1(s0,sp)=

(2)

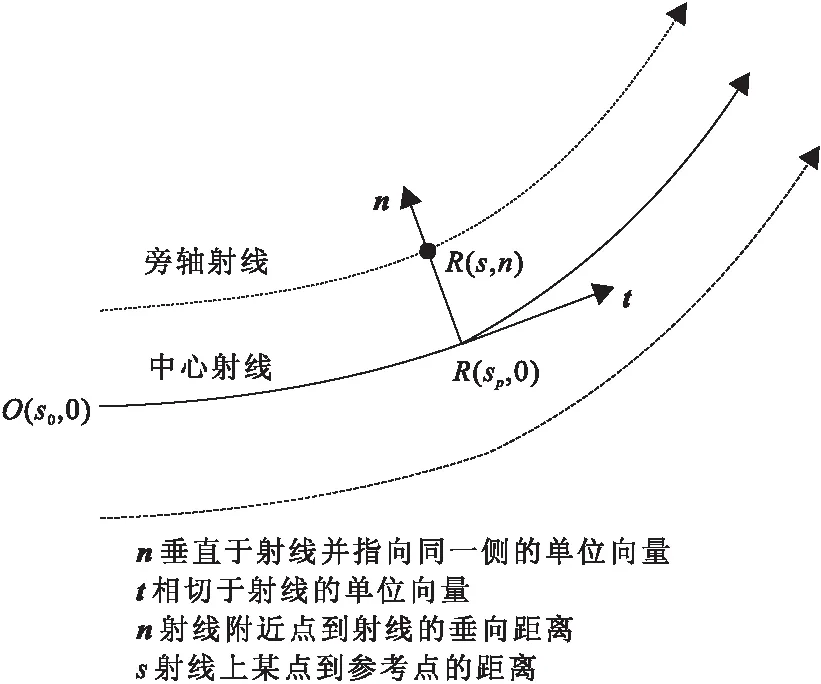
圖1 射線中心坐標系Fig.1 Central ray coordinate system

假定高斯射線束在P點聚焦，且寬度為l0，此時可以求得初始點位置處的動力學射線追蹤參數：

(3)

引入中間變量：

(4)

此時束參數為式(5)。

(5)

其中：s0為初始點到P點的距離；v0為初始點處速度。通常稱由式(5)決定束參數的高斯束為聚焦束。此時束參數的選取是靜態的，僅取決于聚焦位置，不隨射線路徑而變化，不能對整條射線束的能量進行約束。Nowack等[17]進一步修改了復值束參數，構建了動態聚焦束算子，對整條射線束進行約束：

(6)

其中:ωr為參考頻率；[p1(s),q1(s)]和[p2(s),q2(s)]分別為動力學射線追蹤方程的平面波解和球面波解。

對于動態聚焦束逆時偏移，格林函數可以由動態聚焦束的加權積分來表征：

(7)

其中:θ為出射角;Φ(θ)為權值系數;Uθ(s,n)為動態聚焦束：

(8)

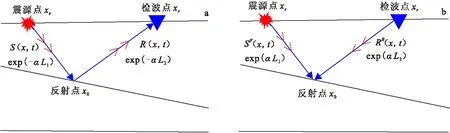
圖2 粘聲介質正演與偏移示意圖Fig.2 Schematic diagram of visco-acoustic media forward and migration(a)正演；(b)偏移

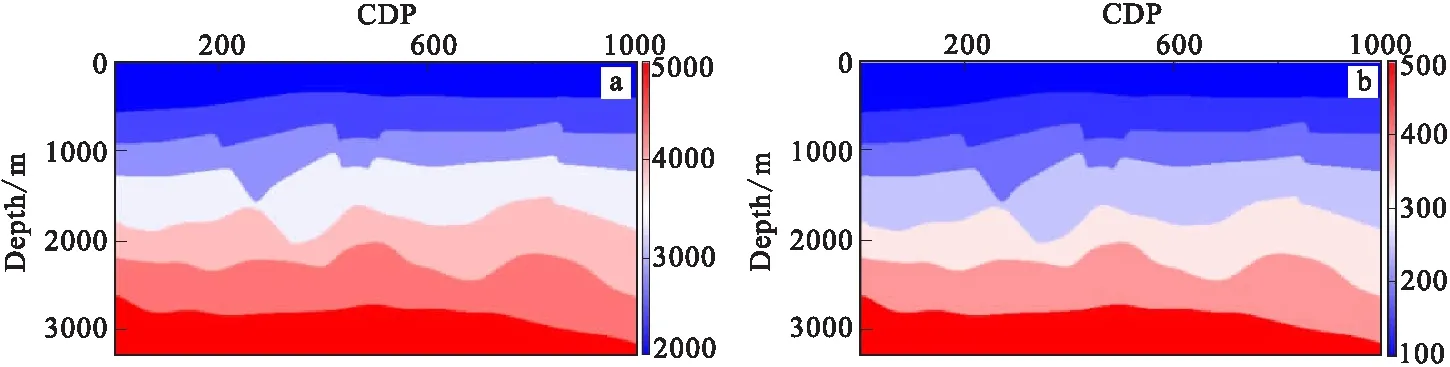
圖3 斷塊模型速度場和Q值場Fig.3 The velocity field and Q value field of fault block model(a)速度場；(b)Q值場

其中:p和q為復值動力學射線追蹤參數，具體可以表示為：

(9)

其中:ε為式(6)表征的復值束參數。動態聚焦束本質上是先給出兩組實初值來求解動力學射線追蹤方程組，然后將計算出的解通過復系數進行線性組合來獲取最終的動力學射線追蹤參數。

1.2 動態聚焦束逆時偏移

記地表在0≤t≤T時刻內接收到地震波場為U0(x,t)，通過Kirchhoff積分可以求得地下偏移域內任一點x0在t0時刻的反向延拓波場：

(10)

其中:xs為震源點；?Ω為閉合區間Ω邊界；?/?nx為外法線方向導數；nx為閉合區間Ω的外法線；G為格林函數。采用動態聚焦束加權積分表征的格林函數(滿足Kirchhoff近似：GGB(x,t;x0,t0)|z=0=0)替代式(10)中的格林函數，可以將反向延拓波場進一步簡化為式(11)。

(11)

震源處正向傳播波場也可以由動態聚焦束表征的格林函數來構建：

(12)

其中:fF(ω)為地震子波的傅里葉變換。

構建完正反向延拓波場，可以依據反射波成像準則，通過兩者的互相關來獲取成像結果，成像公式為式(13)。

(13)

1.3 粘滯性校正

圖2為粘聲介質中正演和偏移示意圖，exp(-αL1)和exp(-αL2)分別為震源處到反射界面和反射界面到接收點的衰減項，S和R分別為震源處和檢波點處的波場，有如下關系：

圖4 斷塊模型試算結果Fig.4 The imaging results of the fault block model(a)聲波動態聚焦束逆時偏移；(b)粘聲高斯束逆時偏移；(c)本文方法

R(x,t)=S(x,t)exp(-αL1)exp(-αL2)

(14)

其中:α為衰減系數；L1和L2分別為震源點到反射界面和反射界面到檢波點的路徑。為了得到準確的成像值，需要通過補償因子exp(αL1)和exp(αL2)對兩個波場進行補償。

地震波在粘滯性介質中傳播，傳播速度為復值，有如下形式：

(15)

其中:Q為品質因子；v0(x)為聲波速度，其實部表征速度頻散特性，虛部則體現衰減效應。對于式(15)中一階項，當1/Q?1時，射線傳播路徑保持不變，吸收衰減效應主要由與頻率有關的復值旅行時體現：

(16)

其中:t(x)為聲波旅行時;t*(x)為沿射線旅行時，具體可以表示為式(17)。

(17)

在粘聲動態聚焦束逆時偏移算法中，采用式(16)所示的復值旅行時替換射線追蹤的旅行時，并對t*(x)有關項取反號，即可實現粘滯性的校正。

1.4 算法流程

粘聲介質動態聚焦束逆時偏移主要分為以下五步：

1)讀入速度場、Q值場和炮記錄。

2)通過運動學和動力學射線追蹤方程，計算中心射線的旅行時、路徑和振幅等信息。

3)根據式(6)構建動態聚焦束算子，構建格林函數，進而實現正反向波場的延拓 (式(11)、式(12))。

4)求取正反向延拓波場的互相關，得到單炮成像結果，并根據式(16)進行粘滯性校正。

5)將所有炮成像結果進行疊加，得到最終的成像結果。

2 模型試算

2.1 斷塊模型

首先采用斷塊模型對算法有效性進行驗證。模型速度場和Q值場如圖3所示，橫縱向網格分別為1 000和550，間距分別為10 m和6 m。正演地震記錄通過有限差分算法獲得，共200炮，采用全接收的方式，炮間隔和道間隔分別為50 m和10 m，時間采樣點為2 000，間隔為1 ms。

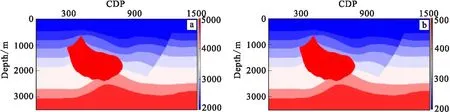
圖5 Hess模型速度場和Q值場Fig.5 The velocity field and Q value field of Hess model(a)速度場；(b)Q值場

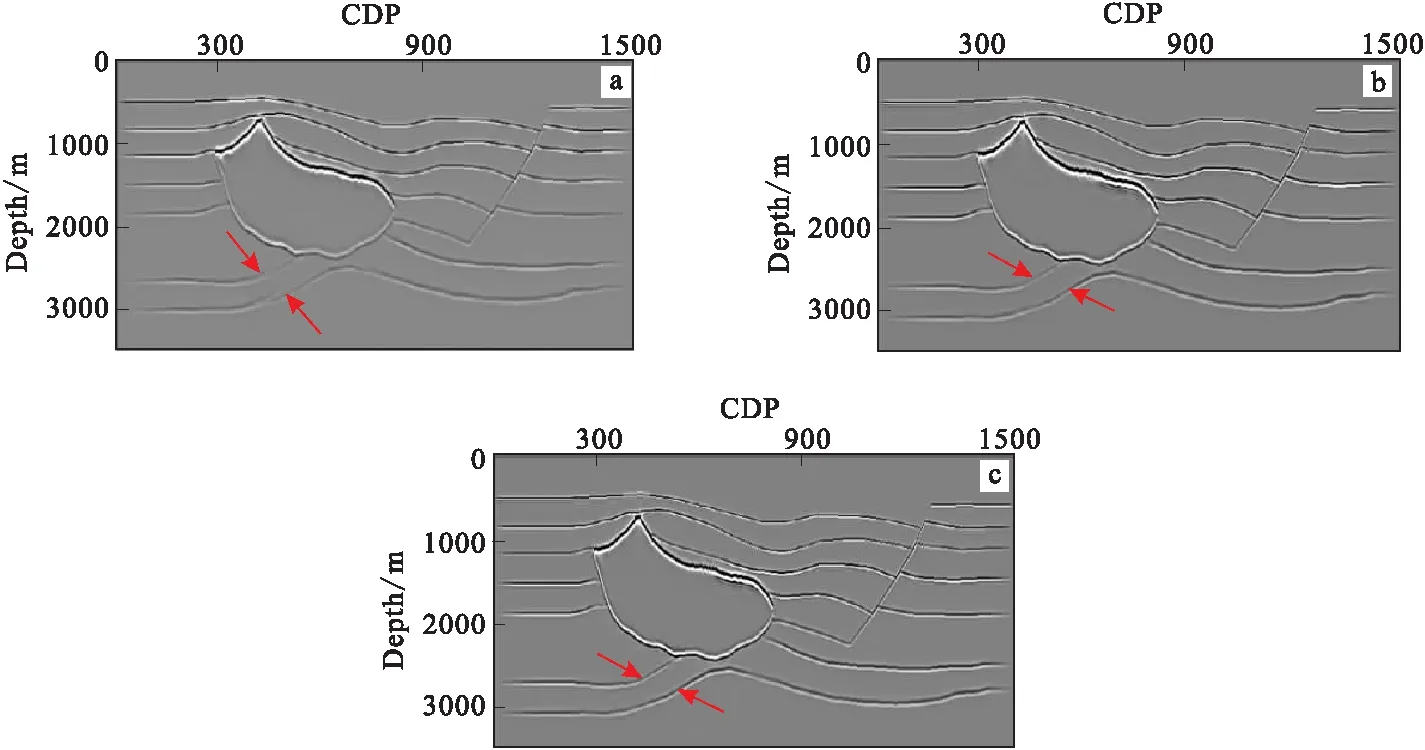
圖6 Hess模型試算結果Fig.6 The imaging results of Hess model(a)聲波動態聚焦束逆時偏移；(b)粘聲高斯束逆時偏移；(c)本文方法

模型試算結果如圖4所示。通過對比可以看出，由于忽略了粘滯性因素，在聲波動態聚焦束逆時偏移結果中，深層能量較弱，同相軸聚焦性也比較差(如圖4(a)中紅色剪頭所示)。而在粘聲高斯束逆時偏移(圖4(b))和動態聚焦束逆時偏移(圖4(c))結果中，深層能量得到了比較好地恢復，同相軸也更加聚焦和連續。相比于粘聲高斯束逆時偏移，本文方法結果中同相軸的能量分布更為均勻，中深層構造成像質量得到了有效提高，反射界面的刻畫也更為清晰，驗證了方法的有效性。

2.2 Hess模型

通過Hess模型驗證算法的適用性。圖5為模型的速度場和Q值場，橫向寬度和縱向深度分別為15 km和3.5 km，網格間距均為10 m。合成地震數據共251炮，每炮1501道接收，炮間隔和道間隔分別為60 m和10 m。地震記錄時間采樣長度為3.0 s，間隔為1 ms。

模型試算結果如圖6所示。可以看出在聲波聚焦束逆時偏移結果中，由于粘滯性的影響，導致深層能量較弱，高速巖丘下方反射層的同相軸連續性和聚焦性也比較差(如圖6(a)紅色箭頭所示)。在粘聲高斯束逆時偏移(圖6(b))和本文方法(圖6(c))的結果中，深層能量得到了有效的恢復，同相軸的連續性和聚焦性也得到了提升。但相比于粘聲高斯束逆時偏移，本文方法結果中同相軸更加聚焦和連續，能量分步也更為均勻，中深層構造的能量聚焦性更為理想，整體剖面更為清晰(如圖6(b)和圖6(c)中紅色箭頭所示)。

3 結論

高斯束逆時偏移是一種兼具計算效率和成像精度的深度域成像算法，具有面向目標成像的能力。筆者首先通過構建動態聚焦束算子，并將其應用在高斯束積分中，表征出動態聚焦束，進而計算出動態聚焦束表征的地震波場，解決了高斯射線束寬度隨傳播距離增加而快速發散的問題；隨后引入與頻率有關的復值旅行時，分別對炮點和檢波點波場的吸收衰減效應進行補償。模型試算表明,本文算法不僅可以將地震波能量約束在一定范圍內，有效提高中深層構造成像質量,而且可以對地層的吸收衰減效應進行有效補償，對反射界面進行更為清晰的刻畫。下一步擬將該方法推廣至各向異性介質。