巖石迭代損傷與膨脹演化規律研究

喬建永，劉冬橋，郭允朋

(1.中國礦業大學(北京)深部巖土力學與地下工程國家重點實驗室，北京 100083；2.北京郵電大學理學院，北京 100876)

0 引 言

自21世紀以來，隨著我國在能源、交通、國防等領域重大基礎設施建設的大規模推進，涌現出一批典型巖石工程，如三峽水電站、葛洲壩水電站、錦屏水電站等大型水電水利工程，青藏鐵路、川藏鐵路等鐵路工程[1]。深入研究各類巖石非線性變形力學特性對這些巖體工程的災害預測及防控起到至關重要的作用，而巖石本構關系不僅是描述各類巖石非線性變形特征的關鍵，也是巖石力學與工程的基石。

巖石本構關系從早期的線性本構關系研究開始，即假定巖石應力-應變關系為一條或幾條理想的直線段，線性本構關系主要包括線彈性模型[2]、雙線性模型[3-6]、三線性模型[7-8]、四線性模型[9-11]和五線性模型[12]等，如圖1所示，其中雙線性模型包括脆性跌落[3](AB段)、應變軟化[4](AC段)、理想塑性[5](AD段)或應變硬化[6](AE段)，三線性模型包括理想彈脆塑性[7](ABD段)或非理想彈脆塑性[8](ACD段)，四線性模型包括線彈性-雙線性軟化-殘余理想塑性[9]、雙線彈性-線性軟化-殘余理想塑性[10](BDE段)或雙線彈性-脆性跌落-殘余理想塑性[11](BCE段)。這些模型針對不同試驗結果具有較好的適用性，且線性本構關系形式簡單，求解方便，但也存在諸多局限，這些模型假定的理想應力-應變曲線具有較大主觀性，它們多將巖石應力-應變曲線劃分為多個階段，分別研究其各階段變形力學機制和本構關系，而忽略了巖石壓縮變形破壞是一個完整過程，故分段式線性本構關系不能實現對應力-應變全過程簡單而統一的描述。實際上，由于巖石自身非連續、非均質、各向異性等特征導致其變形力學行為表現出強烈的非線性特征，這也促進豐富了巖石非線性本構關系的研究，主要成果有雙曲線模型[13]、Loland模型[14]、Mazars模型[15]、Sidoroff模型[16]、Weibull分布模型[17]以及其他分段式曲線模型[18-20]等，如圖2所示。非線性本構關系相對線性本構關系能夠較準確地描述巖石材料受荷過程中的變形響應，但依然多采用分段方式進行描述，無法對巖石變形全過程實現統一完整描述，基于損傷統計的本構模型雖然能夠實現全過程的統一，但不能解釋線彈性現象，且巖石微元強度為何服從Weibull分布也并不清楚。此外，這些模型大都參數較多、形式復雜，給后續推廣或工程應用帶來了極大不便。

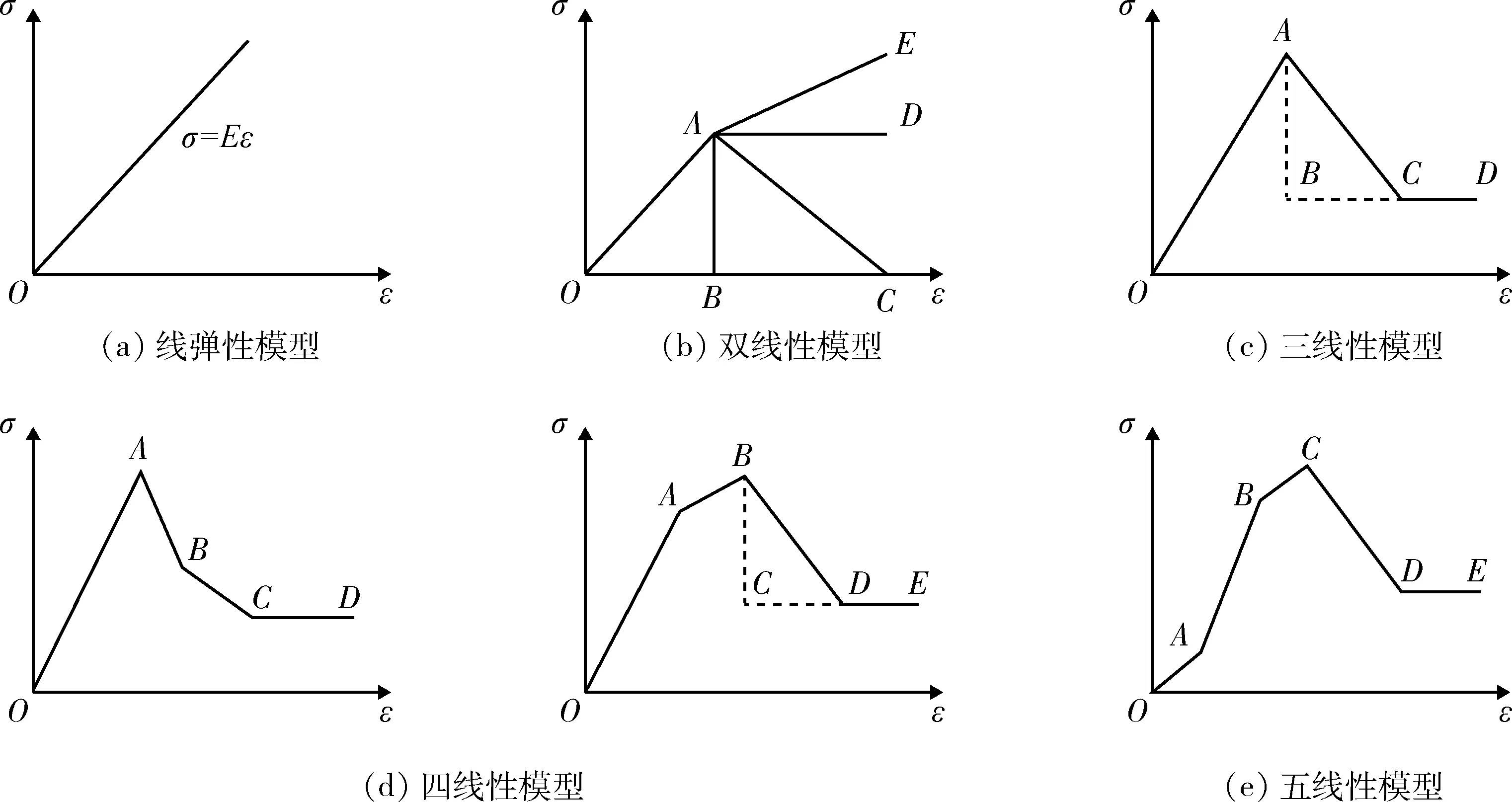
圖1 線性本構關系Fig.1 Linear stress-strain relations

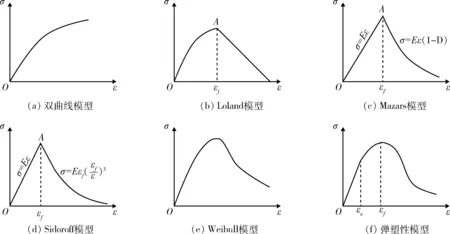
圖2 非線性本構關系Fig.2 Nonlinear stress-strain relations

巖石作為一種天然地質材料，內部隨機分布著大量多尺度初始裂紋、孔隙，其在荷載作用下的變形破壞是一個具有明顯非線性特征的復雜動態過程。究其原因，巖石在外荷載作用下的變形過程是前一時刻狀態向后一時刻狀態的轉變，或者說后一時刻狀態與前一時刻狀態存在某種關系，而該過程可視為一個不斷迭代的過程。因此，從迭代角度出發，建立能夠描述巖石壓縮變形全過程的損傷演化模型及其本構關系，將有助于解釋巖石破壞過程中會出現混沌現象的原因。此外，近年來基于掃描電鏡的巖石力學實驗研究也取得一系列積極進展，觀察到各種巖石的大量微觀結構[21-24]。本文以此為基礎，借助統計力學理論，建立解釋巖石尤其是軟巖迭代膨脹的力學模型，深入研究其物理化學效應引起的膨脹現象。

1 巖石損傷本構模型

巖石由于其復雜的成巖過程，內部都含有或多或少的天然原生缺陷或微裂紋，這些初始缺陷對巖石力學性能產生了強烈的影響，如應力-應變曲線初始非線性變形、峰值強度及有效彈性模量降低、各向異性性質增強等[25]。巖石在外荷載(如靜載或動載)和環境(如溫度、風化作用、水巖作用等)的耦合作用下力學性能逐漸劣化，損傷不可逆累積。受力變形的過程中，初始缺陷或張開性微裂紋首先被壓縮閉合，隨荷載增加新的微裂紋開始萌生發育并擴展演化形成宏觀裂縫直至巖石完全破壞，因此，從損傷演變的角度研究巖石受力變形規律更符合客觀實際。

利用損傷理論研究巖石變形破壞過程的前提是合理定義損傷變量，在此基礎上建立損傷本構方程，并探討損傷演化規律。任建喜等[26]、張全勝等[27]較早地借助CT檢測技術實時監測巖石受荷損傷過程，并基于CT數建立了損傷變量，對應力-應變全過程進行分段，分別給出了本構關系。不少學者考慮到巖石本身存在的微缺陷具有隨機性的特征，假定巖石由無數個微單元組成，并假設這些微單元物理性能服從某種分布函數，如Weibull分布[28-30]、對數正態分布[31]和正態分布[32]等，進而建立了損傷演化模型及適用于不同條件的損傷統計本構模型。還有通過巖石宏觀力學試驗，選取試驗過程中某種宏觀易獲取的動態參量如變形模量衰減[33]、波速變化[34]、裂紋體積應變[35-36]、AE特征參數[37]和能量耗散[38-39]等來定義損傷變量，這其中基于Lemaitre應變等效性假說[40]的彈性模量法應用最為廣泛，也是研究巖石材料損傷演化規律的重要理論基礎。

1.1 損傷變量

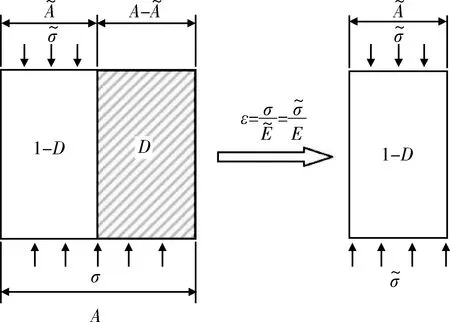
圖3 應變等效性假設示意圖Fig.3 Illustration of strain equivalence hypothesis

對于一維問題，可表示為式(1)。

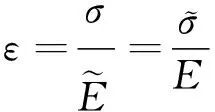
(1)

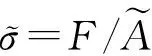
根據損傷變量D以及有效應力的定義[41-42]，可得到式(2)。

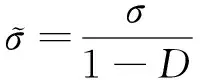
(2)

將式(2)代入式(1)，得到基于應變等效性假說的一維受損材料的本構方程，見式(3)。

σ=(1-D)Eε

(3)

由式(3)可知，得到巖石材料本構方程的關鍵是獲得其損傷變量演化過程的表達式，巖石損傷變量表達式的建立過程如下所述。

1.2 巖石迭代損傷演化模型及本構方程

基于唯象的宏觀統計損傷力學，按照單元破壞、無損的二元假設，把宏觀破壞現象看作是許多微觀單元破壞的平均效應，不均質的微細觀破壞用正態分布或Weibull分布來描述，從宏觀的唯象角度出發定義損傷變量，建立了能夠反映單軸壓縮、三軸壓縮下的巖石損傷統計本構模型[29-32]，但定義的損傷變量沒有與損傷的物理機制相聯系。所以，本節在破壞、無損的二元假設基礎上，建立了一種新的損傷演化模型，引入如下假設。

1) 假設巖石由無數單元組成，單元總數為k(k→+∞)，且單元僅包括無損單元和破壞單元2種類型，如圖4所示。白色部分表示無損單元，記其數量為u，陰影部分表示破壞單元，記其數量為v，則k=u+v。

圖4 巖石微單元結構示意圖Fig.4 Structure diagram of rock micro units

2) 破壞單元不能承受荷載，無損單元在一定條件下都可以轉化為破壞單元，破壞單元不可以轉化為無損單元。

3) 無損單元和破壞單元的面積相等，記為A0。

4) 無損單元為彈性體，滿足胡克定律，彈性模量相等，記為E0。

5) 巖石受載破壞過程滿足應變等效性假說。

6) 不考慮時間效應，即無損單元向破壞單元轉化的過程是瞬間完成的。

根據RABOTNOV[42]提出的損傷變量定義，則損傷變量可表示為式(4)。

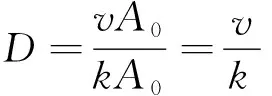
(4)

式中，0≤v≤k，所以損傷變量D∈[0，1]。

已有研究表明，巖石變形破壞是一個從局部開始、漸進演化的過程，最弱處首先產生缺陷，并不斷衍生新缺陷,最終導致巖石破壞[26]，也就是說新缺陷由已存在缺陷和外界條件共同作用產生。因此，可以將巖石變形破壞的損傷演化過程看作是無損單元不斷向破壞單元轉換的過程。結合上述假設及分析，可以將破壞單元看成生物學中的某個單種種群，而巖石變形破壞的損傷演化過程相當于該種群(破壞單元)的增長過程。假設破壞單元增長是無界的，即破壞單元在無限的環境中增長，巖石變形發展不受空間環境等條件的限制，則破壞單元的增長值將和上一時刻的基數成正比[43]，設比值為p，即vn+1-vn=pvn，也就是說巖石內部第n+1時刻的損傷狀態(破壞單元數量)與第n時刻的損傷狀態存在某一函數關系，見式(5)和式(6)。

Dn+1=f(Dn)=(1+p)Dn

(5)

Dn=D0(1+p)n

(6)

式中：Dn=vn/k；p為破壞單元的增長率。式(5)和式(6)表示的缺陷增長形式是呈幾何級數式增長或指數式增長，增長率p與巖石內部破壞單元密度無關。

如果把巖石變形過程中的應變值抽象為該種群(破壞單元)增長模型中的時間，外加荷載抽象為該種群(破壞單元)增長所需的食物，巖石微單元總數量即為該種群(破壞單元)的環境容納量。將巖石變形破壞的損傷演化過程看作無損單元不斷轉化為破壞單元的過程，如果每隔應變間隔Δε測量一次破壞單元的數量，用vn表示第n次的破壞單元數量，則可得式(7)。

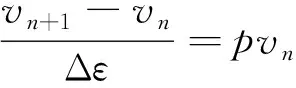
(7)

然而自然界中巖石內部微缺陷受環境空間因素制約，不可能無限制地增長，即破壞單元總數量v不會超過最大環境容納量k，且隨著破壞單元數量不斷增加到接近最大環境容納量k時，破壞單元的增長速度由于環境容量等限制因素將逐漸減緩，直至停止增長，因此破壞單元增長率p不再為常數，而是與破壞單元總數量v和剩余可供轉化為破壞單元的無損單元總數量(k-v)呈某一函數關系。借助生物學一種簡單的、隨種群大小而變化的連續增長模型，即邏輯斯蒂模型(Logistic model)，也稱為阻滯增長模型[44]，可知破壞單元數量隨著應變增加的關系見式(8)。

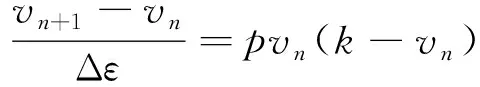
(8)

式(8)轉化為連續變量的形式見式(9)。

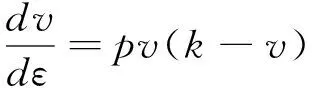
(9)

結合損傷變量的定義(式(4))，式(9)可進一步轉化為式(10)。

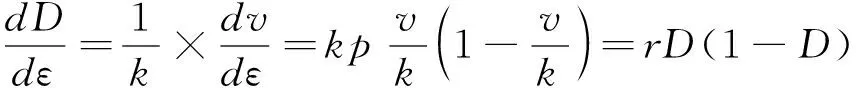
(10)

式中，r=kp為損傷變量的內稟增長率。

對式(10)進行積分，可得到損傷變量的表達式，見式(11)。

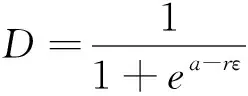
(11)

式中：a=ln(k/v0-1)反映了初始損傷程度；v0為初始時刻破壞單元的數量。

式(11)即為基于Logistic方程建立的巖石迭代損傷演化模型。根據上述假定及描述，破壞單元在有限環境空間下的增長呈現為“S”型，如圖5所示。“S”型增長曲線具備兩個特點[44]：①“S”型曲線有一個上漸近線，即“S”增長曲線最終會漸近于k值，但不會超過最大值水平；②“S”型曲線呈逐漸、平滑的變化趨勢，從曲線斜率來看，起初增長速率較慢，隨后逐漸加快，到曲線中心處存在一拐點，此時增長速率最快，以后又逐漸變慢，直至最終停止增長。

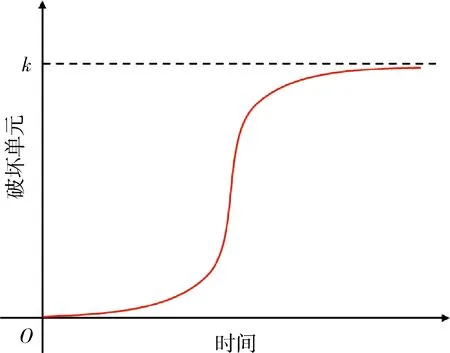
圖5 Logistic增長模型Fig.5 Growth model of Logistic

進一步將損傷變量表達式(式(11))代入一維受損材料的本構方程(式(3))中，即可得到巖石迭代損傷本構方程表達式，見式(12)。

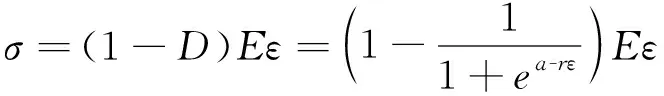
(12)

1.3 模型驗證

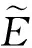
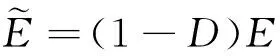
(13)

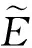
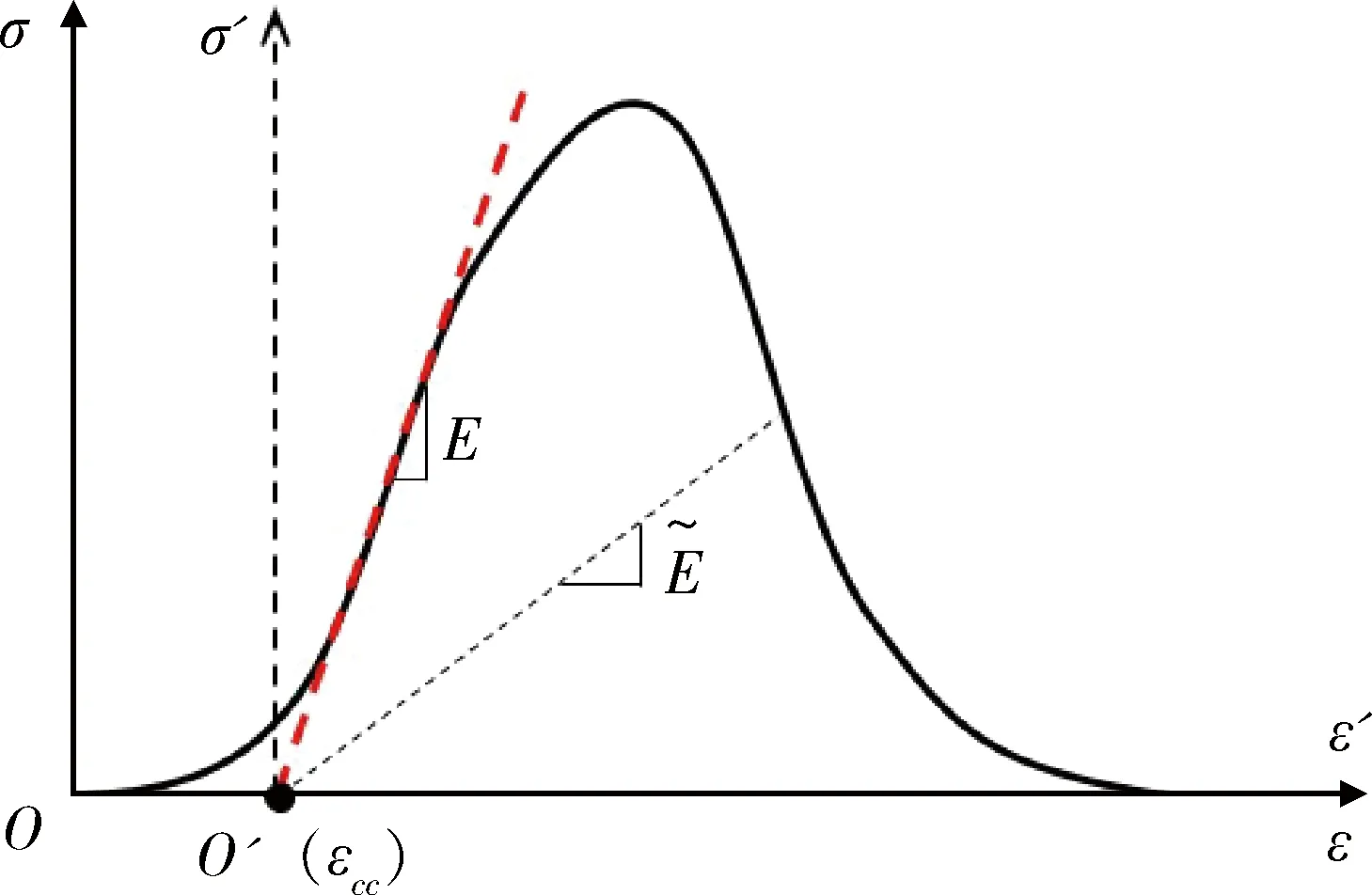
圖6 新坐標系下應力-應變曲線Fig.6 Stress-strain curve in a new coordinate system

根據圖6并結合上述分析可知，新坐標系下巖石迭代損傷本構方程表達式(式(12))可變化為式(14)。

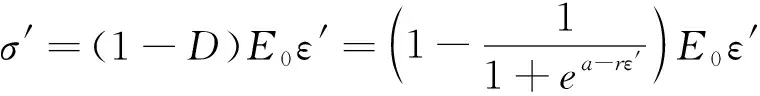
(14)

式中，E0為基準彈性模量，可根據應力-應變曲線彈性段斜率確定。

新坐標系與原坐標系之間存在關系見式(15)，將式(15)代入式(14)，可進一步得到巖石在原坐標系下的迭代損傷本構方程表達式為式(16)。

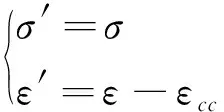
(15)

σ=(1-D)E0(ε-εcc)=

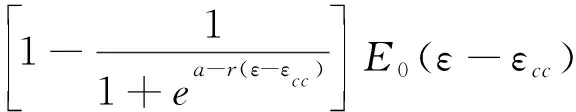
(16)

至此完全建立了巖石單軸壓縮迭代損傷本構方程。 損傷本構方程中各參數確定方法與步驟如下所述。

1) 根據應力-應變曲線彈性段斜率確定基準彈性模量E0。

2) 將線性段反向延長至與應變軸相交(圖6)，交點即為巖石裂紋閉合應變εcc。

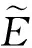
5) 將式(11)進行對數變換可得ln(1/D-1)=a-rε，按該式進行線性擬合即可得到參數a和r的值。

6) 將各參數值代入式(16)，即可得到基于應變等效性假說和Logistic函數的迭代損傷本構方程。

根據砂巖單軸壓縮試驗結果[45]，按照上述步驟計算得到所有參數值為：E0=28.41 GPa，裂紋閉合應變εcc=0.09%，參數a和r分別為12.15和17.92，進而得到砂巖迭代損傷演化模型及其迭代損傷本構方程見式(17)和式(18)。

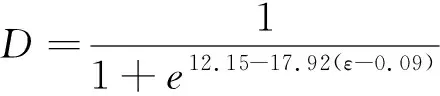
(17)

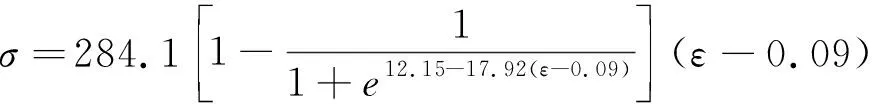
(18)

根據式(17)和式(18)計算得到理論損傷演化曲線、本構關系曲線與試驗數據對比結果如圖7所示。從圖7(a)可以看出，本文所建迭代損傷演化模型與基于變形模量衰減法計算得到的試驗結果吻合良好，且根據該模型可以較清晰地將巖石損傷演化過程劃分為損傷保持、損傷開始、損傷加速、損傷減緩及損傷終止5個階段，這與以往研究結果相符。從圖7(b)可以看出，本文建立的迭代損傷本構方程與試驗數據吻合良好，應力-應變曲線峰前和峰后兩部分都得到了較好的描述，特別是峰前的非線性特征和峰后的應力突降現象，都通過本模型較好地體現了出來。唯一的不足是還不能很好地描述巖石單軸壓縮條件下初始壓密階段的非線性變形特征。但對于工程實際來說，工程巖體大多已經被壓密，所以在研究巖石單軸壓縮條件下變形特性時，很少考慮巖石壓密階段部分。因此，本文建立的巖石損傷迭代本構模型合理，可以用于描述巖石單軸壓縮條件下的應力-應變關系。

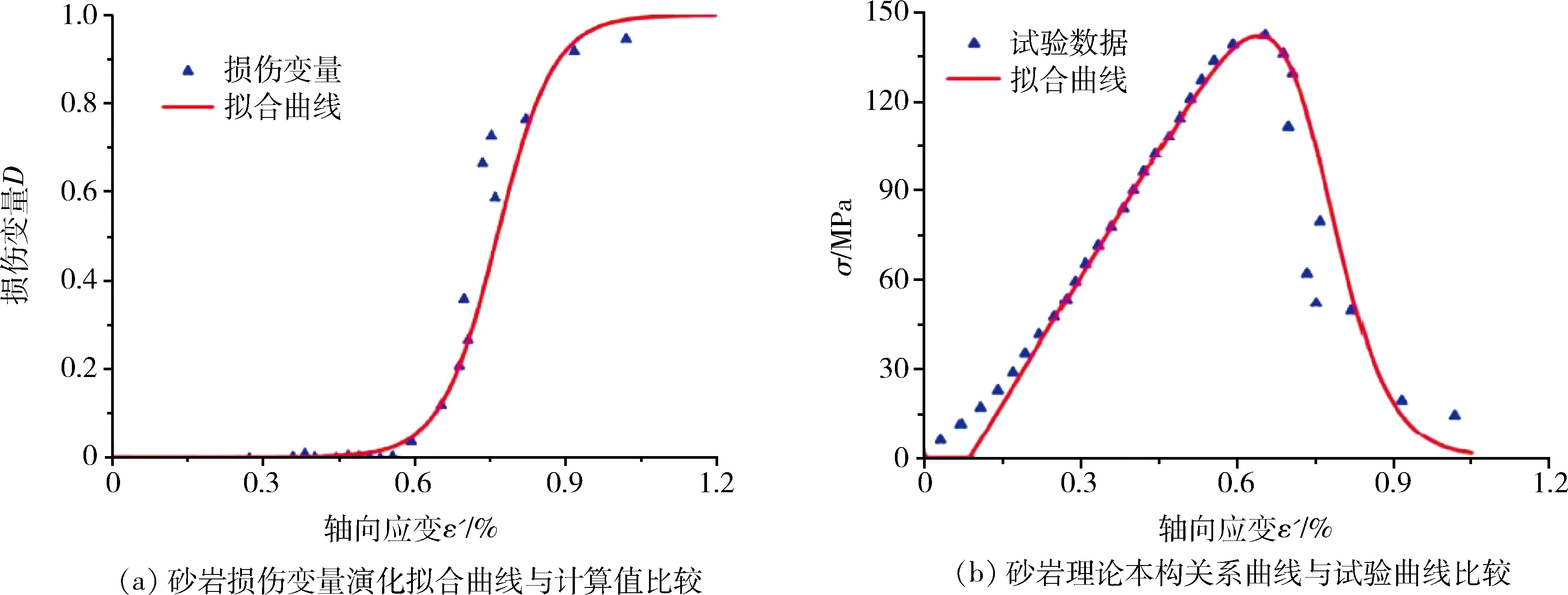
圖7 試驗數據與擬合曲線比較Fig.7 Comparison between test data and fitting curves

2 損傷演化模型的混沌特征

巖石的變形破壞與其內部微裂紋的萌生和演化存在密切聯系，具有顯著的復雜性、模糊性、非線性和不確定性等特征，而混沌理論為研究巖石力學行為的非線性特征提供了新的方法和思路。鄭穎人等[46]通過研究也認為巖石的變形、損傷和破壞是一類非平衡、非線性的動態演化過程，其破壞結果對初始損傷及結構分布具有敏感依賴性，從細觀上講，建立非線性動力學演化模型來描述損傷演化導致失穩破壞的過程才能反映該過程的本質特征。因此，從損傷角度對巖石變形破壞過程的混沌特征進行研究具有合理性。

2.1 損傷演化離散模型

倍周期分岔可用來判別混沌現象，倍周期分岔是指隨著控制參數的增加，將依次經歷1-周期點、2-周期點、4-周期點……的周期加倍的分岔現象，也稱為倍周期分支。1978年，FEIGENBAUM[47-48]發現了由倍周期分岔進入混沌的途徑，而某些條件下的Logistic方程具有典型的倍周期分岔現象[49]，如圖8所示。

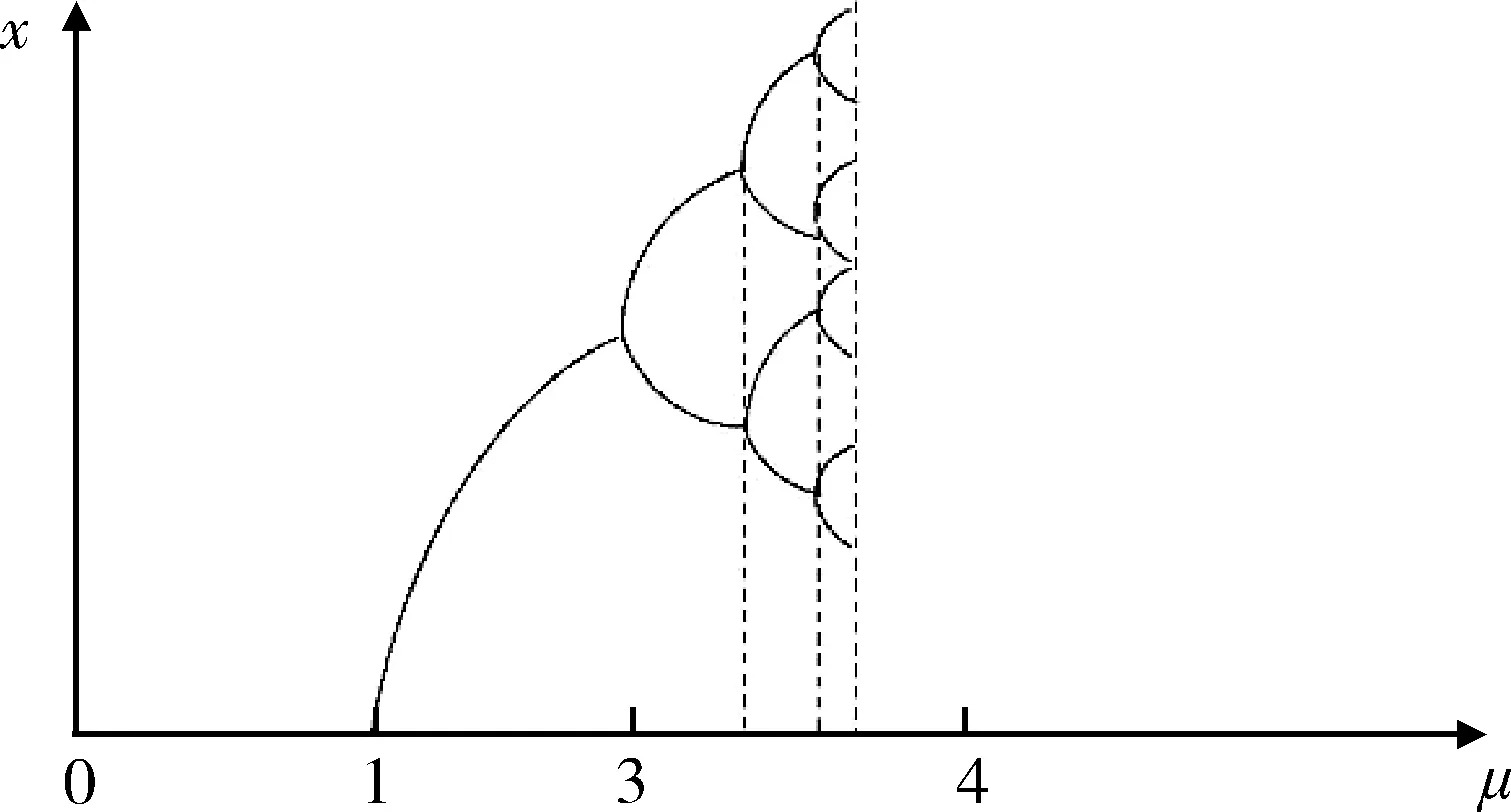
圖8 Logistic方程倍周期分岔現象Fig.8 Periodic bifurcation of Logistic equation

標準的Logistic離散方程見式(19)。

xn+1=Fμ(xn)=μxn(1-xn)

(19)

對于區間I=[0，1]，μ>0，當xn∈I時，隨著μ的增加，Logistic離散方程的解將經歷倍周期分岔進入混沌。此時，從任一點鄰域，都可以找到這樣的點，它的軌道能進入其他任一點鄰域。在I=[0，1]中有這樣的不可數點集，其中任意兩點在映射Fμ的作用下，可以一再地任意靠近，又一再地拉開距離，出現類似于隨機過程的狀態。

對損傷變量演化方程(式(11))進行離散化處理，可以得到單位應變下損傷變量演化的離散模型，見式(20)。

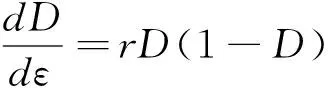
(20)

若每隔應變間隔Δε測量D值一次，用Dn表示第n次的D值，則原來的連續變量D(ε)和ε就變為離散變量(D0，D1，D2，…)和(n=0，1，2，…)，連續微分方程(式(20))就相應地變為式(21)所示的離散差分方程。

(21)

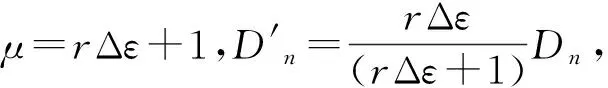
(22)

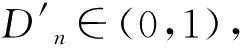
2.2 損傷演化混沌過程

以1.3節中砂巖單軸壓縮變形破壞過程為例，詳細描述巖石損傷演化的混沌特征，其損傷演化方程見式(23)。

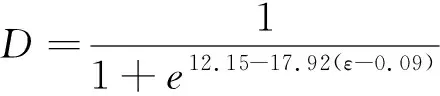
(23)

進一步求導，可得損傷演化方程的微分形式，見式(24)。

(24)

由式(21)可知損傷演化微分方程的離散差分方程為式(25)。

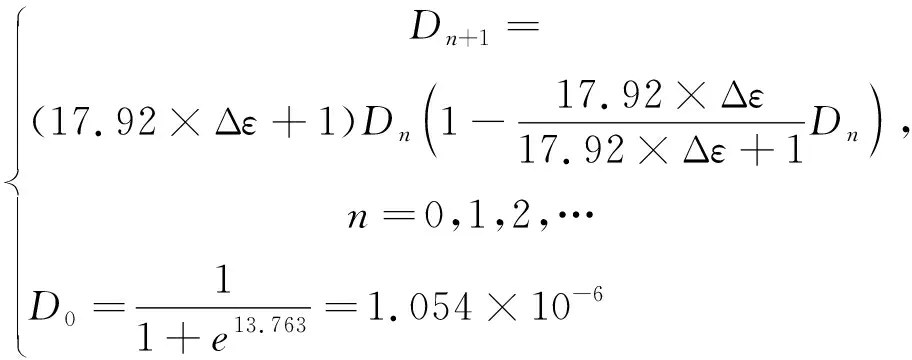
(25)

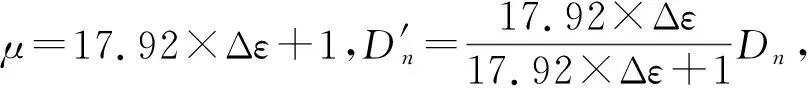
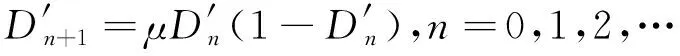
(26)

1) 當0<Δε<0.111 6時，有1<μ<3，其廣義損傷演化過程如圖9所示，其損傷演化終值都將趨于0.5，并保持穩定。

圖9 廣義損傷演化過程(Δε=0.055 8)Fig.9 The generalized damage evolution process(Δε=0.055 8)

2) 當0.111 6≤Δε≤0.143 4時，有3≤μ<3.569 9，其廣義損傷演化過程將隨著Δε的增大出現倍周期分岔現象，圖10(a)和圖10(b)分別為2-周期和4-周期分岔現象。

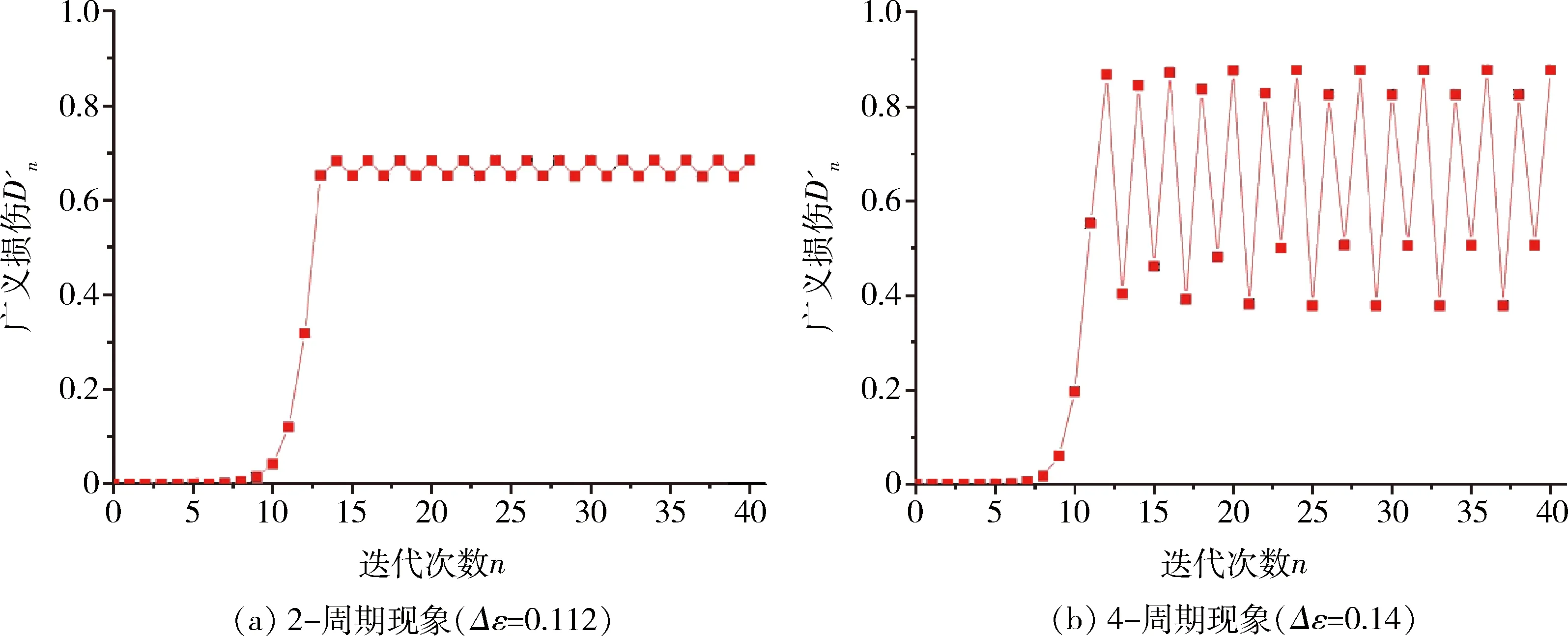
圖10 廣義損傷演化過程(0.111 6≤Δε≤0.143 4)Fig.10 The generalized damage evolution process(0.111 6≤Δε≤0.143 4)

3) 當0.143 4≤Δε<0.167 4時，有3.569 9≤μ<4，其廣義損傷演化混沌過程如圖11所示，隨著迭代的進行，廣義損傷變量可以跑遍區間(0，1)之間的所有狀態，看似隨機實則有序。

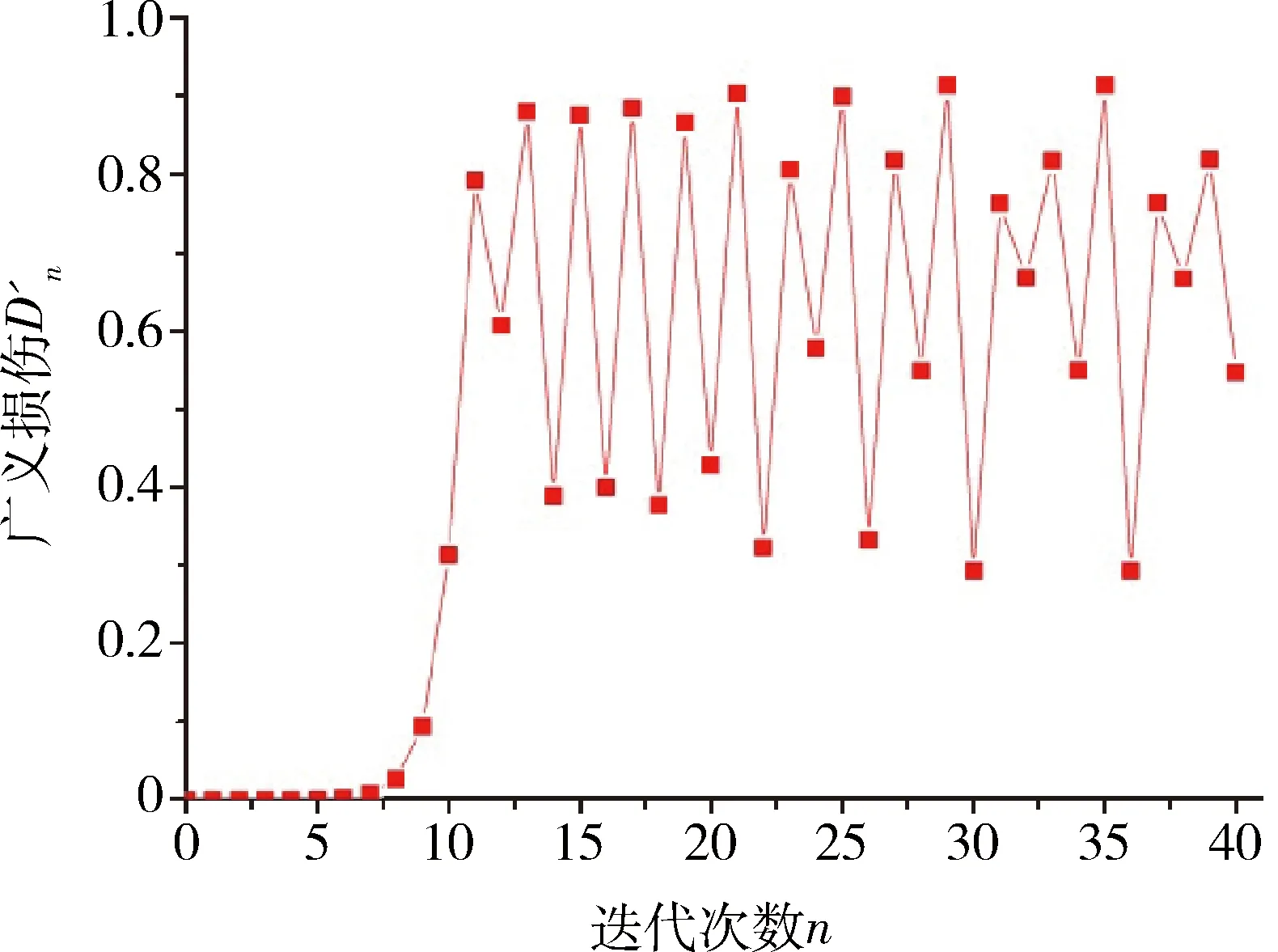
圖11 廣義損傷演化過程(Δε=0.15)Fig.11 The generalized damage evolution process(Δε=0.15)

3 巖石損傷膨脹迭代模型

巖石壓縮變形過程中，損傷不斷增加，其體積呈現先壓縮后膨脹的特性，該膨脹過程也可視為迭代演化的過程。巖石是由不同礦物顆粒組成的非均質連續體，不同礦物顆粒具有不同的膨脹系數，因此，礦物顆粒會產生不協調變形形成局部應力集中，導致巖石體積發生膨脹，當這種膨脹應力超過或者達到礦物顆粒之間黏結強度時，就會破壞掉礦物顆粒之間的連接，進而形成微裂紋。因此，巖石的膨脹特性對于理解巖石破壞有著重要意義。如軟巖膨脹機理被認為是世界性難題[50]，雖然近幾十年圍繞巖石膨脹研究比較豐富，但一直缺少同實驗觀察吻合的有效理論模型。掃描電鏡觀察到的軟巖微觀結構組合元件包括粉砂質顆粒元件和黏土礦物層元件，粉砂質顆粒元件起骨架作用，黏土礦物層元件起膠結的作用，這一微觀結構具有明顯的自相似性，是一種層級結構[21-24]。在研究其膨脹效應時，作為統計力學系統，這種結構同下述金剛石型等級晶格等效。

3.1 金剛石型等級晶格模型及迭代動力系統

金剛石型等級晶格[51]由下述規則迭代生成：首先，設有1個由2個點和1條棱構成的晶格，稱為1-級結構；然后，用每個分支含有2條棱的2個分支的結構取代上面的1-級結構，從而形成2-級結構；接著，用2-級結構代替這一結構中的每一條棱，得到3-級結構。重復上述迭代構造過程，直至無窮多次，最終形成金剛石型等級晶格，如圖12所示。在軟巖微觀結構中，點代表粉砂質顆粒的位置，棱代表黏土礦物的位置。

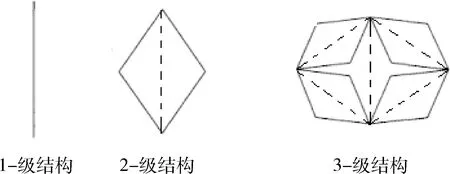
圖12 金剛石型等級晶格Fig.12 The diamond hierarchical lattice

對于上述金剛石型等級晶格體每個格點放置一個粒子σi，每個粒子具有λ種狀態，σi可取1，2，…，λ。將其配分函數記為Z，便得到統計力學中的Potts模型。在軟巖微觀動力學研究中，λ是粉砂質顆粒σi的膨脹、收縮等可能狀態，不同的狀態通過黏土礦物的膠結而產生相互作用。

在統計力學中，通常相變問題的主要任務是研究配分函數零點的分布問題，這往往十分困難。按照楊振寧和李政道的相變理論[52-53]，把exp(J/kT)記為自變量z(其中，J是相互作用常數，k是Boltzmann常數，T是溫度)，如果把z開拓到復數域，則配分函數自然解析開拓為一個復變函數，它在復數域上的零點稱為Yang-Lee零點，配分函數零點的極限集與實軸的交點即為相變點的考察對象。

為了深入分析粒子之間的相互作用和統計平均效應，統計力學提出把多粒子問題轉化為少粒子問題的研究思想，即重整化群方法的“粗粒化”思想，其關鍵是尋找一個稱為重整化變換[49]的映照，使這一過程實現。在二維情況，重整化變換往往是有理映照或整函數映照。20世紀80年代初，物理學家們發現[49,54]，重整化變換的復動力系統的混沌集(Julia集)對應上述物理模型中Yang-Lee零點的極限集。

復動力系統理論考慮復解析映照R的迭代序列的收斂性問題。記R的k次迭代為Rk。為了使得迭代能夠延續下去，要求R的定義域和值域是一致的。粗略而言，如果序列{Rk}在某一點z的局部鄰域內的收斂一致性比較好，則稱這個點z為穩定點，全體穩定點組成的集合F(R)稱為Fatou集，其余集J(R)稱為Julia集。F(R)為開集，J(R)為閉集。進一步把Fatou集的每個連通分支稱為Fatou分支，從而把R的定義域按序列{Rk}收斂的穩定性進行了二元劃分：Fatou集和Julia集。Fatou集稱為穩定集，Julia集總是非空集；Fatou集是完全不變集，即F(R)在R映照下的前像和后像仍然是F(R)，這是設計計算機程序繪制Julia集圖像的基本依據。淹沒點是指Julia集上那些不在任一Fatou分支邊界上的點，由此可見，淹沒點的存在性反映出是Julia集的拓撲結構的復雜性[55]。 另外，{Rk}在J(R)上具有周期點的稠密性、拓撲傳遞性、對初始值的敏感依賴性，這三條性質說明R的迭代動力系統在J(R)上呈現混沌狀態[49]，故Julia集稱為動力系統的混沌集。

3.2 淹沒點、玻璃態轉變和軟巖膨脹

2020年，JIANG等[56]構建了長程作用下的廣義金剛石型等級晶格上的Potts模型，這是一種鐵磁作用和反鐵磁作用競爭的金剛石Potts模型。具體構造過程：在上述金剛石型等級晶格的構造過程中，每一次總是“去除”一條棱，而“替代”為金剛石型結構，這次保留原來的棱(如圖12所示用虛線表示的棱)，在上述Potts模型的基礎上，在保留的棱(虛線)上加一個長程作用τ，這個模型的重整化變換U為一個帶雙參數τ和λ的四次有理映照族[56](其中參數τ代表長程作用)。

通過這族重整化變換迭代動力學的研究，可以發現：在鐵磁作用和反鐵磁作用競爭的廣義金剛石Potts模型中，形成鐵磁鏈和反鐵磁鏈的逐級競爭，該族重整化變換的Julia集里，存在實參數τ以及某個自然數參數λ，使得Julia集上有淹沒點位于正實軸上的情況出現。從Yang-Lee零點的物理意義可見，這種淹沒點的出現對應玻璃態轉變現象。玻璃態轉變是物理學和材料科學中的前沿科學難題，它是2005年國際期刊《Science》公布的125個人類面臨的最具挑戰性的科學前沿問題的第47個問題。

近年來，玻璃態轉變的研究一直在不斷發展。從20世紀50年代出現的自由體積理論到現在還在不斷完善的模態耦合理論以及其他眾多理論，都只能解釋玻璃態轉變中的一部分現象，完備的玻璃態轉變理論遠未建立。在眾多玻璃態轉變的理論模型中，幾乎沒有同基礎數學具體前沿成果緊密相關的模型[56]。本文的模型建立了上述軟巖Potts模型、玻璃態轉變與復動力系統的淹沒點概念之間的聯系。

綜合以上討論，取λ=2，即軟巖微觀顆粒取膨脹和收縮兩種狀態，就可以給出軟巖自由膨脹的相變分類：有限次相變、無窮次相變以及玻璃態轉變[57]。圖13所描繪的Julia集就是在不同長程作用下(對應于不同的τ值)，上述軟巖Potts模型Yang-Lee零點的極限集。

圖13 不同參數τ對應的重整化變換U的Julia集Fig.13 The Julia sets for different parameters

上述分類說明，軟巖膨脹的物理化學效應既可能引起有限次物理相變，也可能引起無窮次物理相變，甚至使軟巖體進入異常復雜的玻璃態轉變狀態，這同軟巖膨脹機理的復雜性高度契合。

4 結 論

本文基于應變等效性假說的變形模量損傷衰減理論，通過分析巖石壓縮變形過程中迭代的演化特征，得出了巖石損傷演化規律，并從迭代角度建立了模擬該損傷演化規律的方法，在此基礎上推導了一種新的巖石損傷本構模型，進而分析了損傷演化過程的混沌特征；基于掃描電鏡觀察到的軟巖微觀結構，建立了統計力學模型，分析了軟巖膨脹的物理化學效應，主要得出以下結論。

1) 基于微缺陷迭代生長提出的損傷演化模型，實現了對巖石壓縮變形全過程損傷演化規律統一、完整的描述，且損傷表達式清楚、物理意義明確。

2) 借助應變等效理論，從損傷迭代的角度，得到了巖石應變軟化的本構方程表達形式，該本構方程僅用一個簡單函數就描述了巖石壓縮應力-應變全過程曲線，通過與試驗數據對比，模擬結果吻合度高。

3) 對提出的損傷演化模型進行適當變換后，廣義損傷可以表示為離散的方程，分析了其分岔及混沌特征，表明巖石在外載荷作用下的變形破壞過程是一個具有混沌特征的損傷演化過程，從而解釋了巖石變形破壞過程具有混沌特征的原因。

4) 軟巖膨脹的物理化學效應既可能引起有限次物理相變，也可能引起無窮次物理相變，甚至使軟巖體進入異常復雜的玻璃態轉變狀態，這同軟巖膨脹機理的復雜性高度契合。