基于人工魚群算法的二輥液壓軋機輥縫PID控制器優化

羅彩玉，劉明

（1.阿克蘇職業技術學院機電工程學院，新疆 溫宿 843100；2.華北理工大學電氣工程學院，河北 唐山 063210）

當前，軋機已經成為鋼鐵制造領域的一個必不可少的設備，軋帶產品質量受到輥縫控制效果的顯著影響［1-2］。為進一步提高軋帶尺寸控制精度，需對輥縫進行精確控制并增強抗干擾能力［3-4］。

樊立萍等［5］綜合運用PID方法與模糊邏輯控制方法建立了一種模糊自適應PID控制技術，并對輥縫進行了控制測試，結果顯示采用該控制方法表現出了比傳統PID方法更優的控制效果。崔佳梅等［6］在測試二輥液壓軋機輥縫控制性能的過程中依次對神經網絡、PID方法與無模型自適應方法進行了比較分析，結果顯示，采用無模型自適應方法能夠滿足快速收斂的要求，并且大幅減小了穩態誤差，使模型獲得了更強抗擾動能力。李波等［7］主要對二輥液壓軋機輥縫控制運行過程的非線性特性進行了研究，并分析了引起控制參數與輸入不穩定性的各項因素，設計得到一種高效的自適應反步滑模控制技術，根據仿真結果可知，自適應反步滑模控制器能夠實現高精度跟蹤的效果，并且實現了良好的魯棒性能。王憲等［8］針對二輥液壓軋機輥縫控制引起參數波動，以及在外界因素作用下引起軋輥不能達到準確壓下位置的過程開展了研究，通過模糊輸出反饋的方式來滿足同步控制輥縫伺服系統運動過程的要求，根據仿真結果可知，在系統中加入模糊輸出反饋條件后除了可以縮短同步時間以外，還能顯著降低跟隨誤差。李建雄等［9］設計了一種利用Anti-Windup抗飽和魯棒性來實現的動態輸出反饋控制算法，將該算法應用到了規格為650 mm的輥縫系統中，結果顯示該算法能夠滿足有效性要求。劉希等［10］將魯棒H∞控制器應用于二輥液壓軋機輥縫控制中，以此實現參數攝動等情況的仿真測試，結果顯示該H∞控制器達到了優異跟蹤性能并實現了參數攝動的良好魯棒性。彭珍瑞等［11］為數控機床進給伺服系統構建了一個仿真模型，設計了一種以人工魚群算法（artificial fish swarm optimization，AFSO）進行優化的PID控制器，并將其跟傳統Ziegler-Nichols方法實施了對比分析.通過仿真測試發現，采用人工魚群PID控制方法獲得了比傳統形式PID控制方法更優的控制效果，達到了更快的動態響應速率并提升了穩定性。徐秀芬［12］深入分析了對電液比例系統進行PID控制時的參數整定過程，建立一種通過蟻群算法（ant clony optimization，ACO）實現的PID參數優化方案，同時確定了具體控制步驟，結果發現VACA-PID控制器同時獲得了優異靜、動態性能，充分滿足了電液比例系統的調控需求。

綜上所述，現階段關于二輥液壓軋機輥縫控制方面的研究基本都是關于系統階躍響應方面的內容，并且工況條件也比較單一，并不能實現對復雜工況下的軋機系統控制要求。針對以上情況，本文對二輥液壓軋機輥縫控制進行了研究，并為系統控制過程構建了開環傳遞函數，同時運用ACO與AFSO優化了PID控制器的各項參數，最后利用Simulink對比了優化處理后的系統響應速率與抗干擾性。

1 二輥液壓軋機輥縫控制方案

1.1 二輥液壓軋機輥縫控制原理

軋機工作輥的執行機構控制如圖1所示，有2個液壓缸，能實現對工作輥垂向運動過程的控制功能。液壓缸位移通過測厚儀將信號傳輸至計算機，其運動過程通過調節伺服閥閥芯位置來實現，由此獲得精確的輥縫［13］。對輥縫進行控制的結構原理如圖2所示。

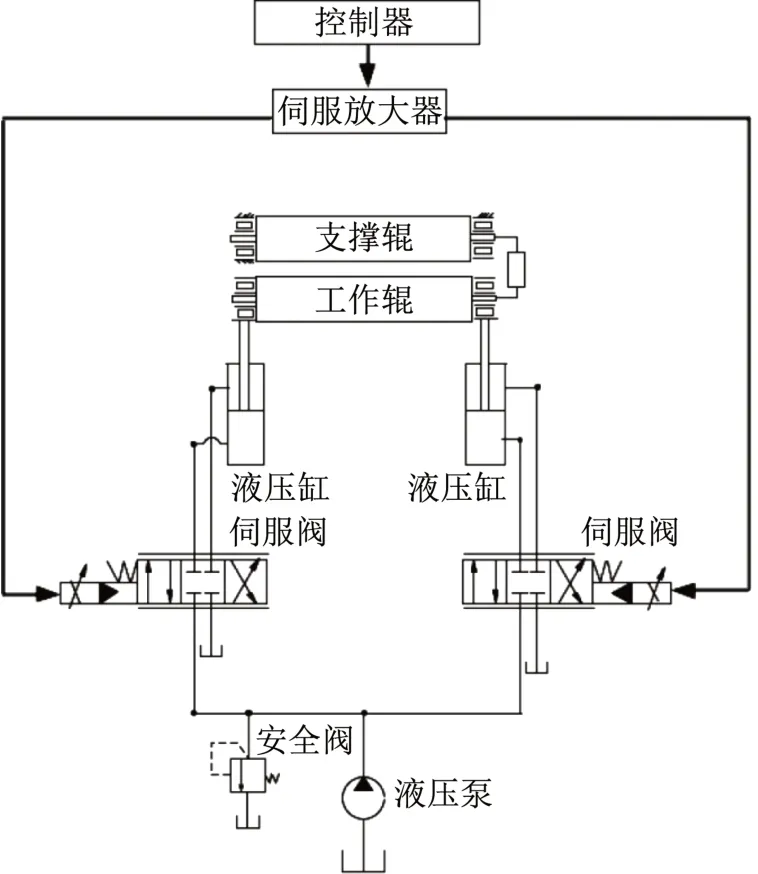
圖1 二輥液壓軋機輥縫控制原理Fig.1 Roll gap of two high hydraulic mill control schematic diagram

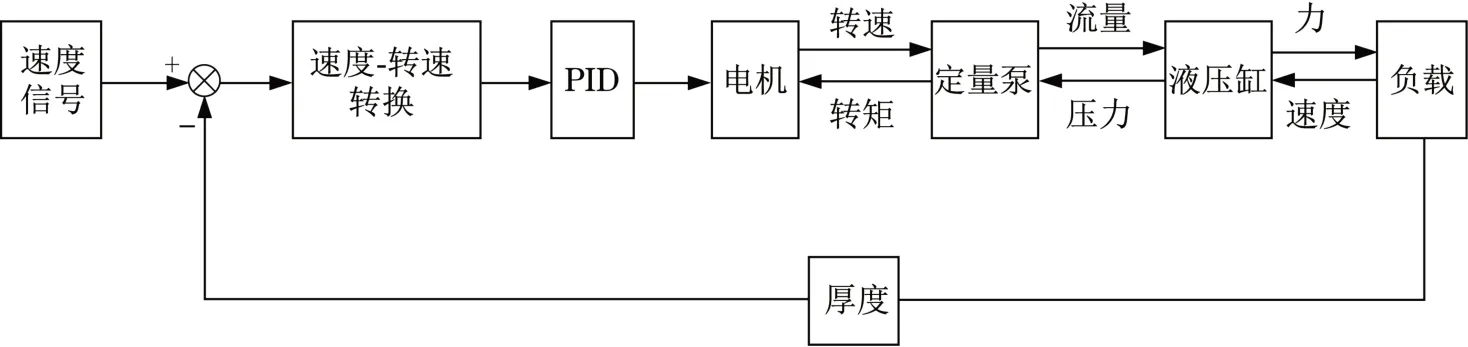
圖2 二輥液壓軋機輥縫控制方案Fig.2 Roll gap of two high hydraulic mill control scheme

按照以下條件設置系統各項參數：選擇原液壓缸作為本系統液壓缸，半徑為39 mm；流量系數介于0.60～0.62之間，本實驗采用0.62。主要參數具體見表1。

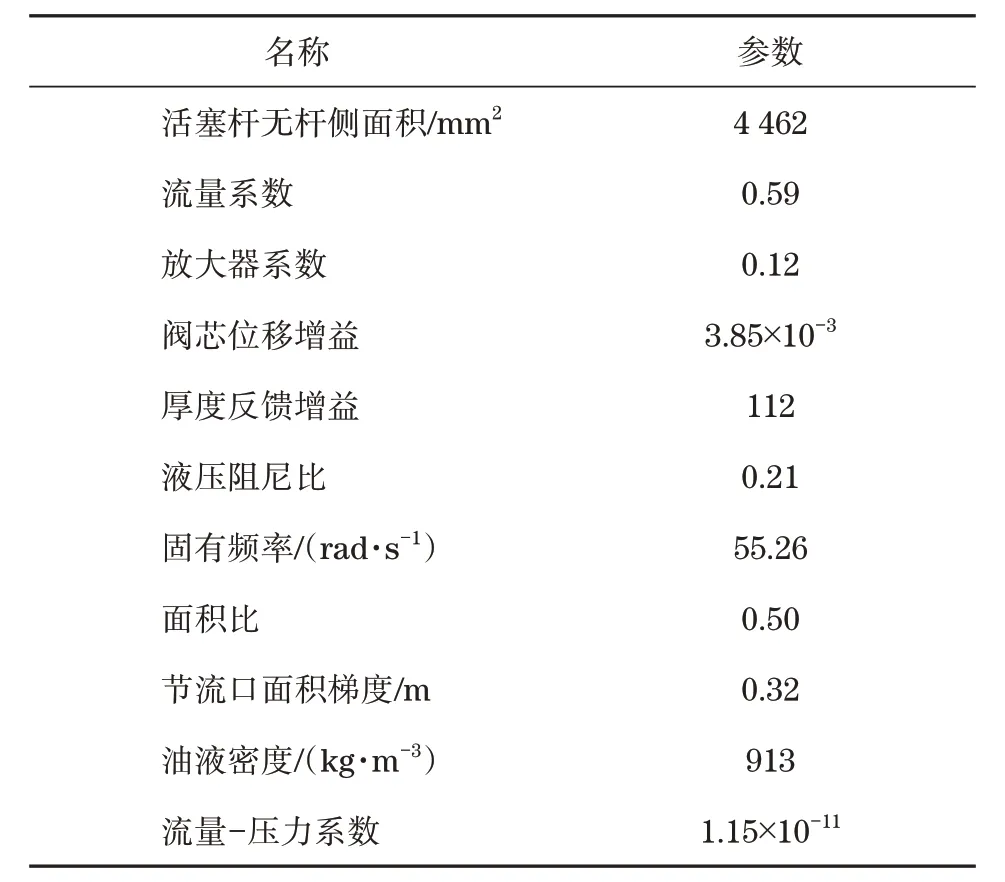
表1 系統主要參數Tab.1 Main system parameters

1.5 控制器設計

通過模仿螞蟻行為建立ACO，不同螞蟻間根據各自釋放的外激素物質來實現信息傳輸過程，當螞蟻沿運動路徑產生的信息素不斷積累后，便可以實現蟻群集體行為的正反饋效果［14］。采用ACO優化PID的具體框圖如圖3所示，優化參數取值見表2。

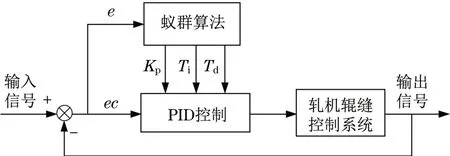
圖3 ACO優化PID結構Fig.3 Block diagram of ACO optimized PID parameters

表2 ACO優化參數Tab.2 ACO optimization parameters

利用AFSO對PID的各參數進行了優化。AFSO則是針對魚群容易聚集到營養豐富的區域進行模仿得到的一種最優解計算方法。AFSO可以實現全局快速收斂的功能，與ACO相比能夠有效避免發生局部最優的情況［15］。采用AFSO對PID參數進行優化的具體過程如圖4所示。

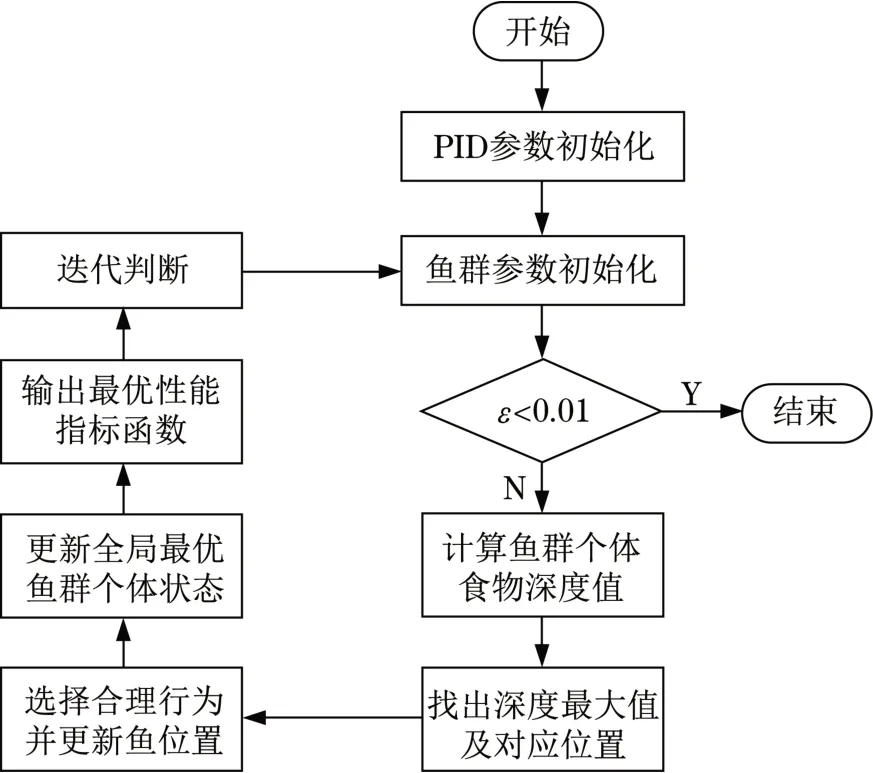
圖4 AFSO優化PID流程Fig.4 AFSO optimization PID process

2 仿真分析

根據二輥液壓軋機輥縫控制傳遞函數，利用Simulink構建如圖5所示的仿真模型。本研究在系統中加入了階躍信號與特定頻率的隨機信號，之后對2種算法進行系統響應與抗干擾性優化的效果進行了分析。

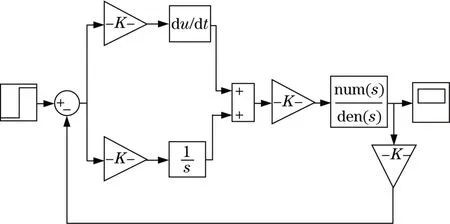
圖5 仿真模型Fig.5 Simulation model

2.1 階躍信號分析

首先將優化后的PID參數加入模型中，再對系統設置階躍信號，通過仿真獲得分別以2種算法進行優化后的系統階躍響應狀態。通過超調量、穩態誤差、調整時間來評價階躍信號的響應性能，未施加干擾力下階躍響應結果見表3。由表3可見，AFSO獲得了比ACO更低的超調量，降低幅度達到13.61%，同時縮短了21.00%的調整時間，并且穩態誤差也減小近30.00%，以上結果表明，采用AFSO可以達到比ACO更優的響應性能。

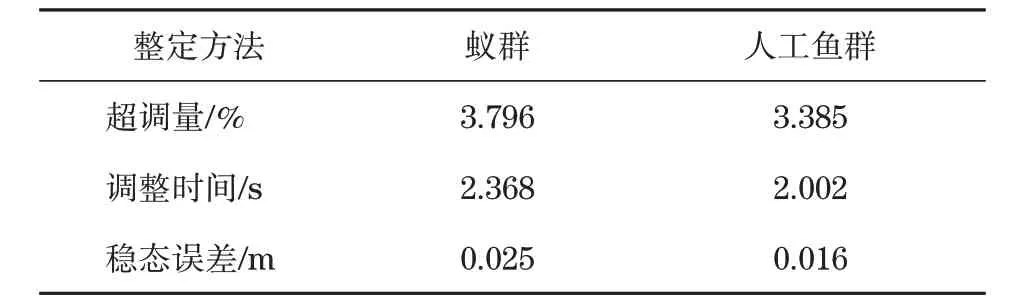
表3 未施加干擾力下階躍響應結果Tab.3 Step response results without interfering force applied

同時在系統中加入階躍信號與干擾力信號，對比了2種算法優化后的系統抗干擾效果。對2種算法優化后的系統受到干擾力作用情況下產生的響應差異性結果見表4。經對比發現，受到干擾力作用后，采用AFSO優化的系統，響應曲線超調量下降了12.58%，調整時間縮短了14.58%，穩態誤差降低了25.00%。

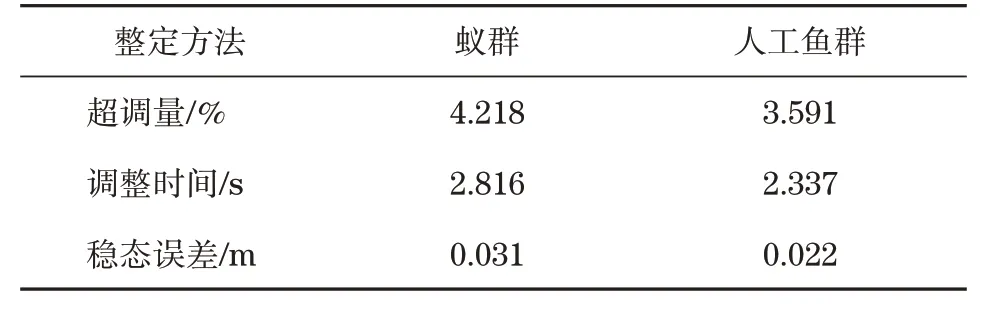
表4 未施加干擾力下階躍響應結果Tab.4 Step response results with interfering force applied

2.2 隨機信號分析

選擇Random Number模塊在系統中加入不同頻率的隨機信號。通過仿真獲得如圖6所示的系統響應曲線。

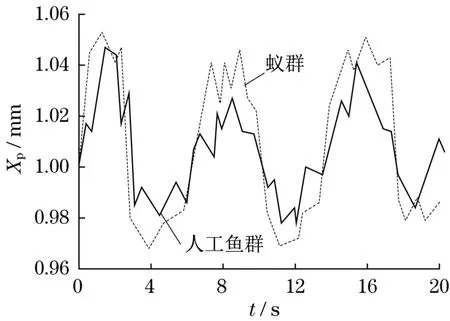
圖6 隨機信號下系統響應結果Fig.6 System response results under random signal

響應波動范圍算法對比結果見表5，給出了對各頻率隨機信號下形成的系統響應波動情況。由表5可知，逐漸提高隨機信號頻率后，2種算法獲得的響應曲線都發生了波動性降低的變化趨勢；在所有頻率條件下，AFSO都比ACO表現出了更低的隨機信號響應曲線波動范圍，表明AFSO具備比ACO更優的響應控制效果。

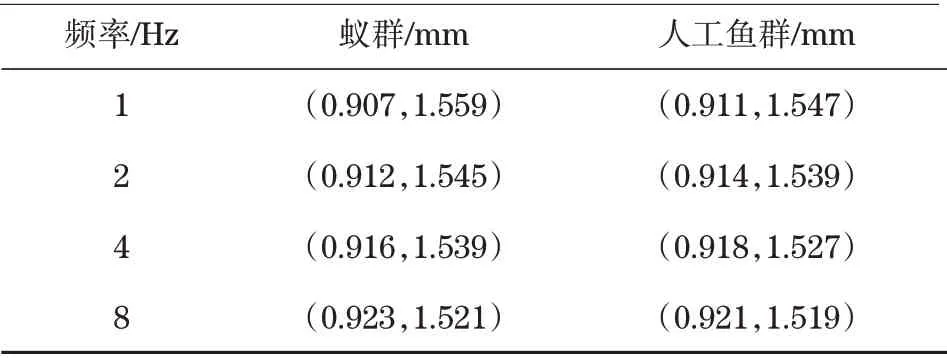
表5 響應波動范圍結果統計Tab.5 Statistics of response fluctuation range results

3 結論

（1）階躍信號未施加干擾力下，AFSO獲得了比ACO更低的超調量，降低幅度達到13.61%，同時縮短了21.00%的調整時間，并且穩態誤差也減小近30.00%，表明采用AFSO可以達到比ACO更優的響應性能。

（2）階躍信號施加干擾力下，采用AFSO優化的系統，響應曲線超調量下降了12.58%，調整時間縮短了14.58%，穩態誤差降低了25.00%。

（3）逐漸提高隨機信號頻率后，AFSO都比ACO表現出了更低的隨機信號響應曲線波動范圍，表明AFSO具備比ACO更優的響應控制效果。