定向滲流誘導的非均質凍結壁力學特性分析

王彬，榮傳新，程樺，蔡海兵

（1.安徽理工大學土木建筑學院，安徽 淮南 232001；2.安徽理工大學深部煤礦采動響應與災害防控國家重點實驗室，安徽 淮南 232001；3.安徽理工大學安全科學與工程博士后科研流動站，安徽 淮南 232001；4.中煤礦山建設集團有限責任公司博士后科研工作站，安徽 合肥 230091）

0 引言

凍結壁作為擬開挖土體周圍的臨時支護結構其受力特性分析一直是人工地層凍結法研究領域的重要問題。在該問題的研究初期，凍結壁被視為均質材料，其力學分析過程被簡化為厚壁圓筒的受力問題［1］，該分析方法較為簡單，因此被工程上廣為應用［2-3］。然而由于受凍結管熱傳導距離的影響，凍結壁內部的溫度并不相等，而是隨著與凍結管的距離的變化而變化［4-5］，這導致凍結壁內部的強度是不均勻的，因此將凍結壁視為均質材料進行計算存在一定誤差。胡向東等［6-7］首次提出將凍結壁視為功能梯度材料，并基于摩爾-庫倫強度準則推導了單排管以及雙排管凍結壁的應力計算公式；王彬等［8-9］根據該思路并基于D-P強度準則也對單排管以及雙排管凍結壁的應力公式進行了推導，并首次提出了三排管非均質凍結壁的應力計算公式［10］；曹雪葉等［11-12］基于雙剪統一強度準則推導得出了材料性質呈拋物線變化的FGM凍結壁的應力計算公式。由于凍結壁并不是單獨存在于土體中的，因此凍結壁周圍的未凍土體與凍結壁之間存在相互作用，并且凍結壁內部土體開挖會對凍結壁的受力狀態產生一定的影響，楊維好等［13-15］推導得出了考慮與圍巖相互作用的凍結壁彈性、彈塑性以及塑性應力解；胡向東等［16-18］推導得出了考慮開挖卸載作用的凍結壁承載力的計算公式；王彬等［19］基于上述理論，推導得出了考慮卸載作用以及與周圍未凍土體相互作用的非均質凍結壁的應力計算公式。

流動的地下水作用下人工凍結溫度場的分布規律與無流速時相比存在較大差異［20-25］，其中位于上游區域的凍結壁厚度明顯小于下游區域，凍結壁不再是一個規則的厚壁圓筒，傳統的“厚壁圓筒”分析方法不再適用；并且凍結壁內部的溫度分布規律也發生了較大變化，位于凍結管布置圈上游以及下游的溫度場存在明顯差異［20-22］，因此現有的溫度曲線等效方法［6-7］也不再適用。同時，現有文獻中關于凍結壁彈塑性分析的研究，通常只采用一種屈服準則進行推導與計算［6-10］，不能全面地反映出凍結壁的力學特性。針對上述問題，本文將基于定向滲流誘導的非均質凍結壁溫度場的分布規律，考慮不同的凍土強度準則，對定向滲流誘導的非均質凍結壁的應力計算公式進行推導，并結合工程算例對不同流速作用下的凍結壁的力學特性進行計算分析。

1 定向滲流誘導的非均質凍結壁溫度場分布規律

在流動的地下水作用下，位于上游位置的凍結壁最遲交圈，對應相同的凍結時間，該位置的凍結壁厚度最小，且同時受到地層壓力以及水壓的作用，因此該位置是整個凍結壁“最危險位置”，該位置凍結壁的強度決定了整個凍結壁的穩定性。已有研究成果表明，在無流速時，凍結壁截面的溫度最低點位于凍結管布置圈上；而定向滲流誘導的非均質凍結壁“危險截面”的溫度最低點位于凍結管布置圈下游位置處［23］；同時，二次函數可以較好地反映相鄰凍結管中間區域截面的溫度場分布規律［6-11］。因此，為了便于采用數理方程描述“危險截面”的溫度分布規律，以凍結溫度場最低溫度點所在位置作為凍結壁分區界線，分別用兩段二次函數曲線近似替代溫度場的分布曲線［6-11］。

不同流速的地下水作用下凍結壁“危險截面”的溫度曲線計算模型如圖1所示。將凍結壁的內徑用R0表示，擬開挖邊界的半徑用R1表示，凍結壁的外徑用RH表示，凍結壁截面上任一點的半徑用R表示。為了便于公式的推導，用相對半徑r=R/R0表示凍結壁截面內的任一點。

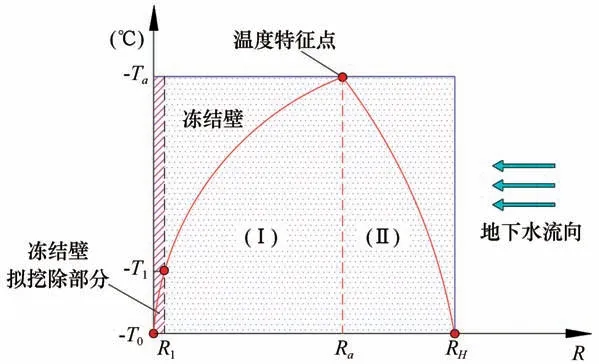
圖1 不同流速的地下水作用下凍結壁溫度分布模型Fig.1 Temperature distribution of the"dangerous section"of the frozen wall under the action

在凍結壁內徑處：R0/R0=1；

在凍結壁擬開挖邊界處：R1/R0=r1；

在凍結壁外徑處：RH/R0=rH；

假設凍結壁“危險截面”的溫度分布規律滿足以下二次函數表達式：

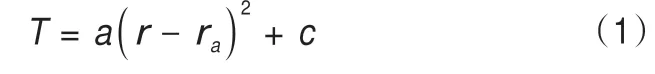
式中：ra為截面溫度最低點所在位置；a、c為待定常數。

溫度場的邊界條件為：

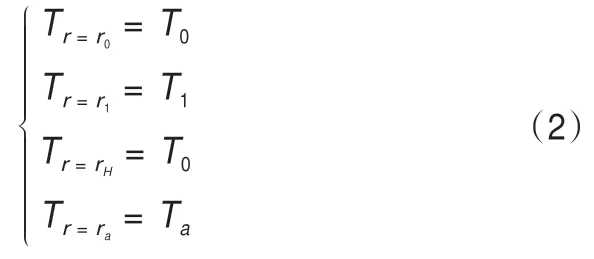
式中：T0（℃）為土體的凍結溫度，即凍結鋒面處凍土的溫度；T1為凍結壁擬開挖邊界的控制溫度，該溫度一般為-3℃；Ta（℃）為凍結壁截面的最低溫度，Ta與地層中水流速度V相關。

將邊界條件（2）代入（1）可得凍結溫度場的曲線函數為：

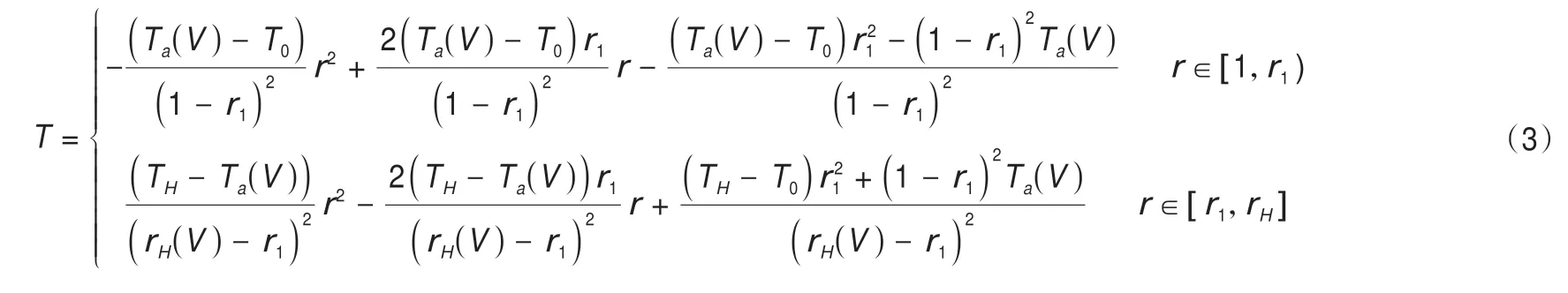
2 凍土力學特性

2.1 凍土強度參數

已有研究成果表明，不同土性凍土的彈性模量E、黏聚力c與溫度存在近似的一次函數關系［19］。

結合凍結壁“危險截面”溫度場的分布規律，將凍結壁的彈性模量以及黏聚力用二次函數［6-11］表示：

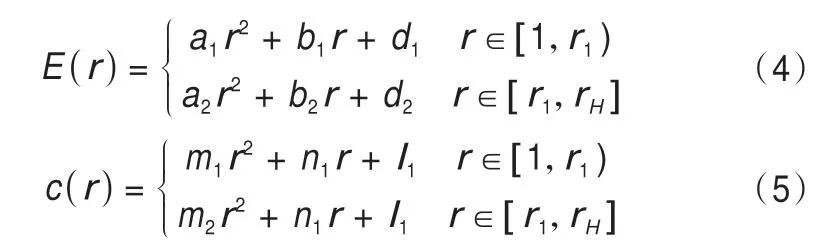
式中：a1，a2，b1，b2，d1，d2以及m1，m2，n1，n2，l1，l2分別是與溫度分布曲線相關的參數，且上述參數都是與地下水流速V相關的參數。

假設凍結前后土體的泊松比μ與內摩擦角φ保持不變［6-8-19］。

2.2 凍土強度準則

認為凍結壁進入塑性后體積不可壓縮，對于軸對稱平面應變問題有［13-15］：

因此幾種常用的強度準則經推導后可以用下式表示［14-15］：

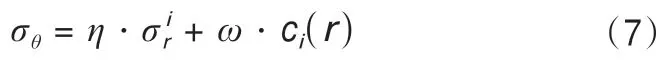
式中：η以及ω的表達式如表1所示。

表1 不同屈服準則中η以及ω的表達式Table 1 Expressions ofηandωin different strength criteria

3 凍結壁應力計算公式

3.1 地下水作用下凍結壁力學模型

為了便于計算，將受流動的地下水影響形成的不規則的凍結壁簡化成厚度與“危險截面”相等的厚壁圓筒。凍結壁“危險截面”的力學模型如圖2所示。

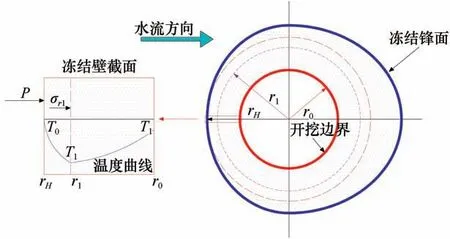
圖2 地下水作用下凍結壁“危險截面”力學模型Fig.2 Mechanical model of"dangerous section"of frozen wall under groundwater

考慮開挖卸載作用后，無窮遠處未凍土體的等效應力［16-18］為：

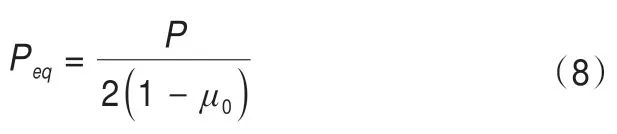
式中：P為土體的原始水平應力；μ0為土體的泊松比。

在力學模型中，凍結壁的應力場邊界條件為：

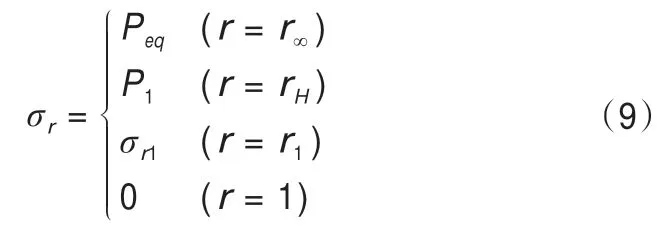
3.2 凍結壁彈性應力計算公式

當凍結壁處于彈性平面應變狀態時，滿足以下基本方程：

平衡方程［26］：

幾何方程［26］：

平面應變狀態下的物理方程［26］：

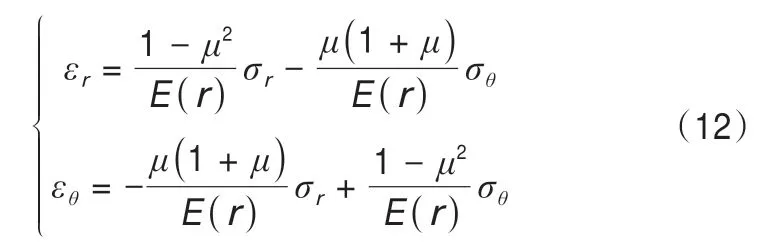
引入應力函數ψ，將σr，σθ通過ψ表示［6-9］：

結合式（10）～（13）可得：

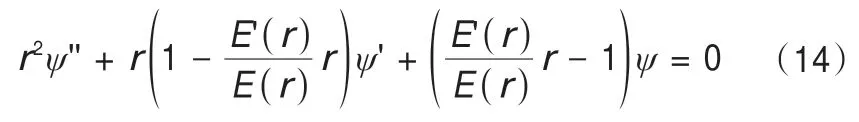
將凍結壁周圍未凍土體視為均勻、彈性介質，則周圍土體的彈性應力計算公式［26］為：

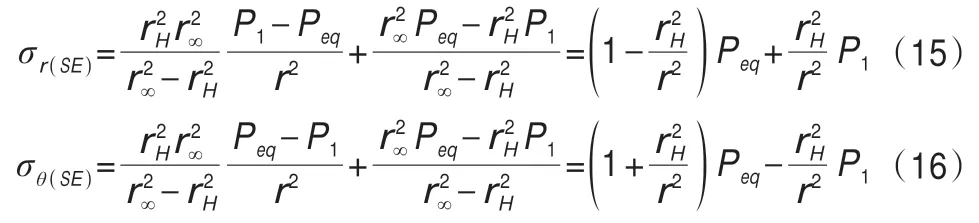
由（4）可知，凍結壁的彈性模量隨著r變化，將彈性模量E（r）表達式代入（14）可得：

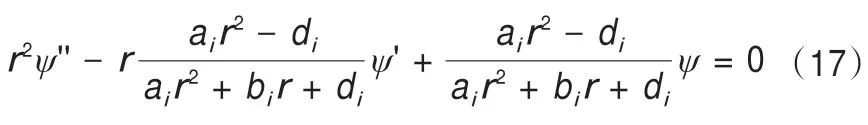
通過求解可以得出（17）的通解為：

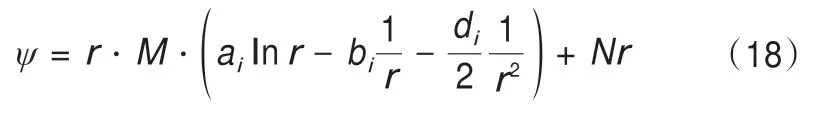
式中：i=1，2分別表示靠近開挖邊界一側以及靠近未凍土體一側。

將應力邊界條件帶入（18）可以得到靠近開挖邊界一側的凍結壁彈性應力計算公式為：

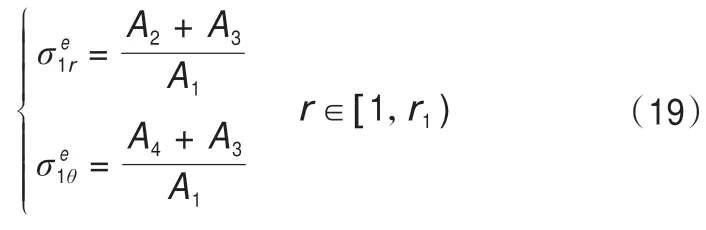
同理，可以得到靠近未凍土體一側的凍結壁彈性應力計算公式為：

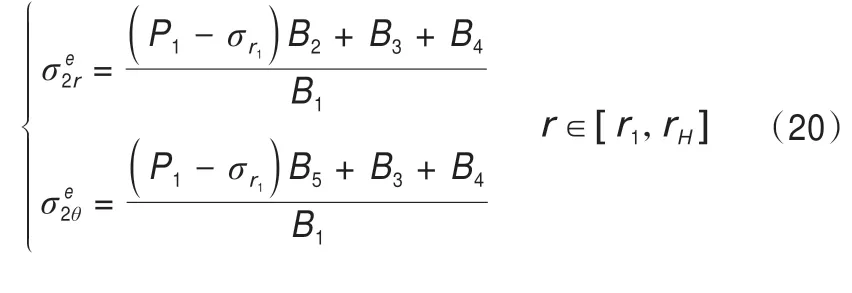
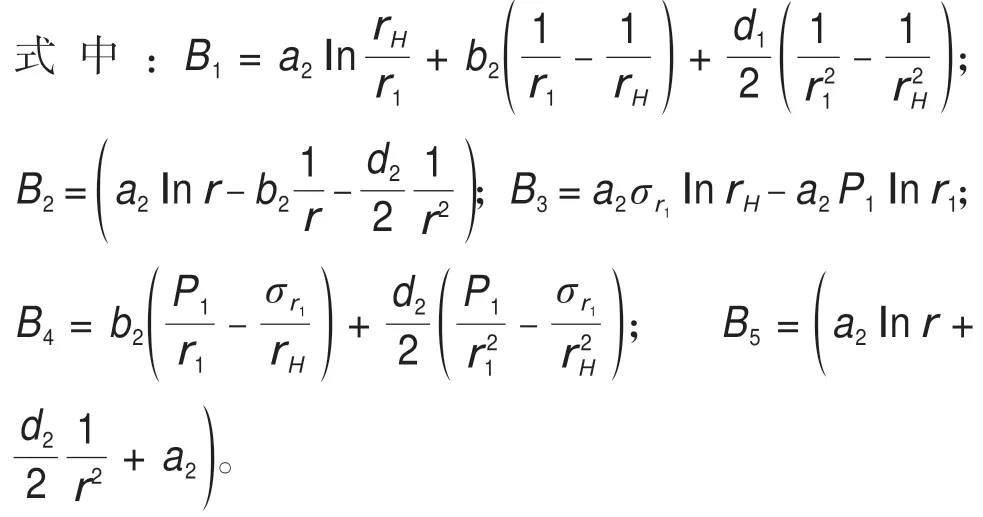
凍結壁rH以及r1處的位移連續條件為：

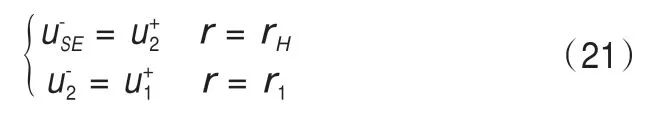
在平面軸對稱問題中有：

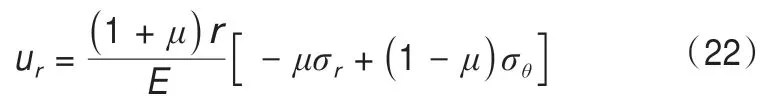
因此可以得出下式：

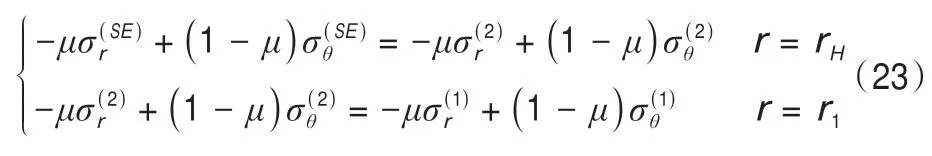
由方程（23）可以求得P1以及σr1。

3.3 凍結壁彈塑性應力計算公式

當凍結壁的外荷載大于凍結壁的彈性極限承載力時，凍結壁進入彈塑性狀態，沿著凍結壁“危險截面”由內向外依次分為塑性區以及彈性區。

塑性區應力平衡方程為［27］：

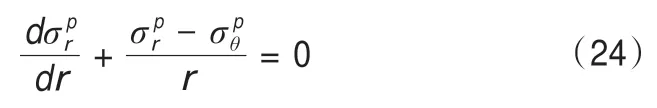
將強度準則代入（24）得：

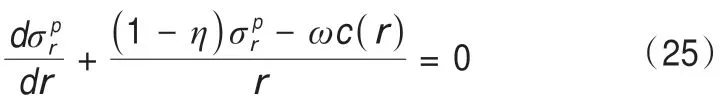
通過求解可以得出凍結壁塑性區徑向應力的通解為：

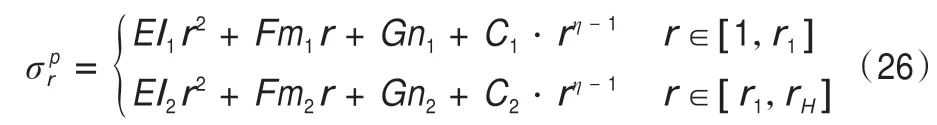
根據r=1以及r=r1處的應力邊界條件可以求得Ci的值為：

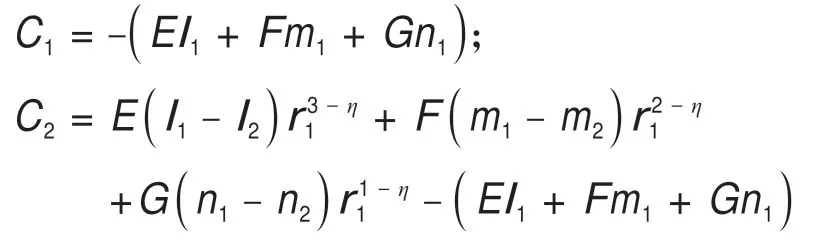
凍結壁塑性區的環向應力可以通過下式求得：

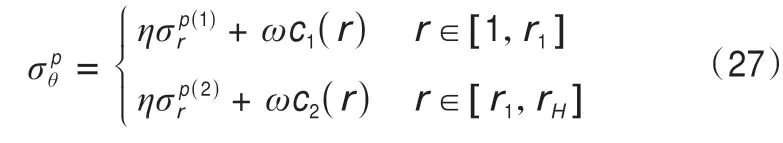
假設凍結壁塑性區半徑為ρ。當ρ∈[1，r1)時，在區間[1，ρ)上，凍結壁處于塑性狀態；在區間[ρ，rH]上，凍結壁處于彈性狀態。凍結壁的應力計算公式為：

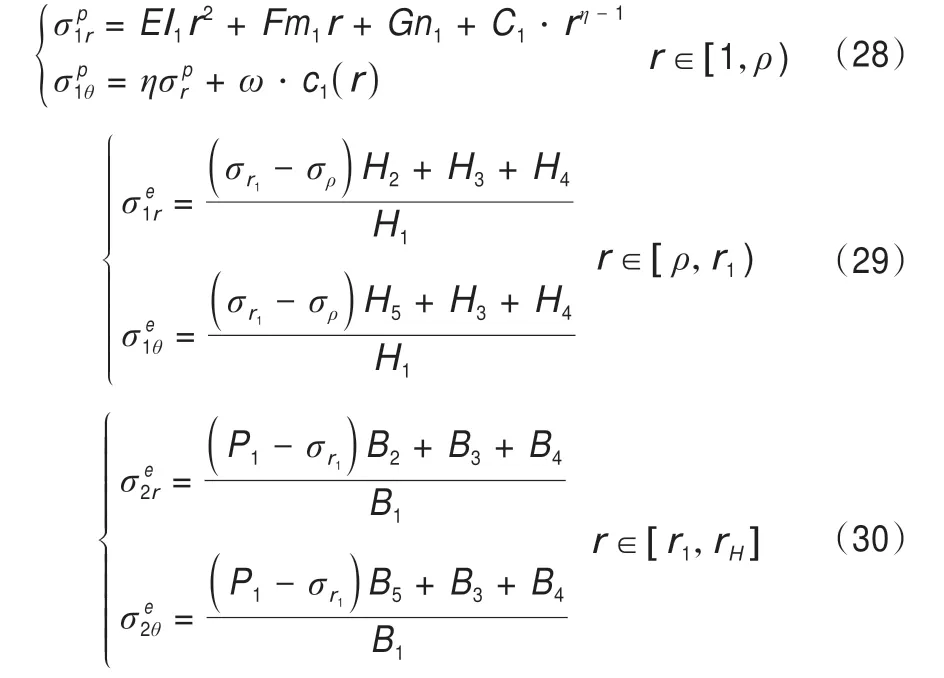
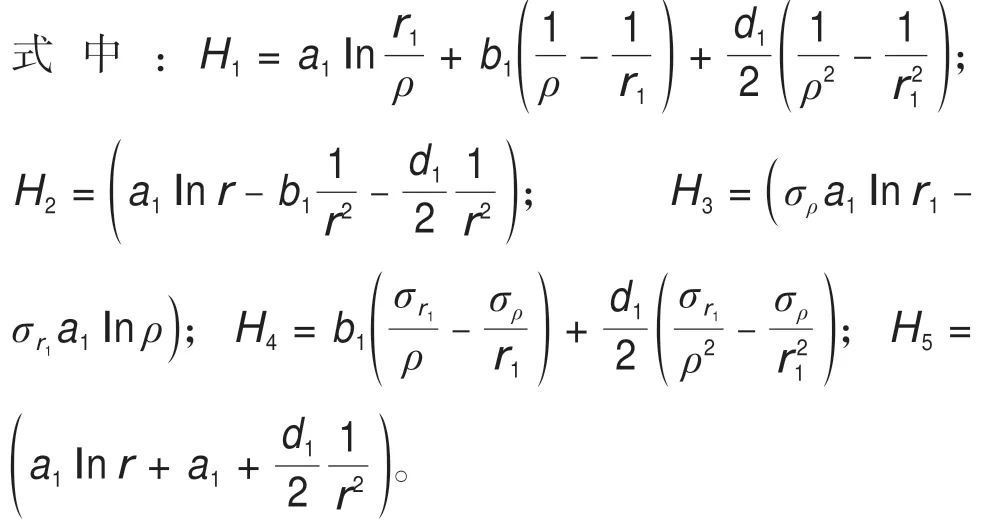
當ρ∈[r1，rH]時，在區間[1，ρ)上，凍結壁處于塑性狀態；在區間[ρ，rH]上，凍結壁處于彈性狀態。凍結壁的應力計算公式為：

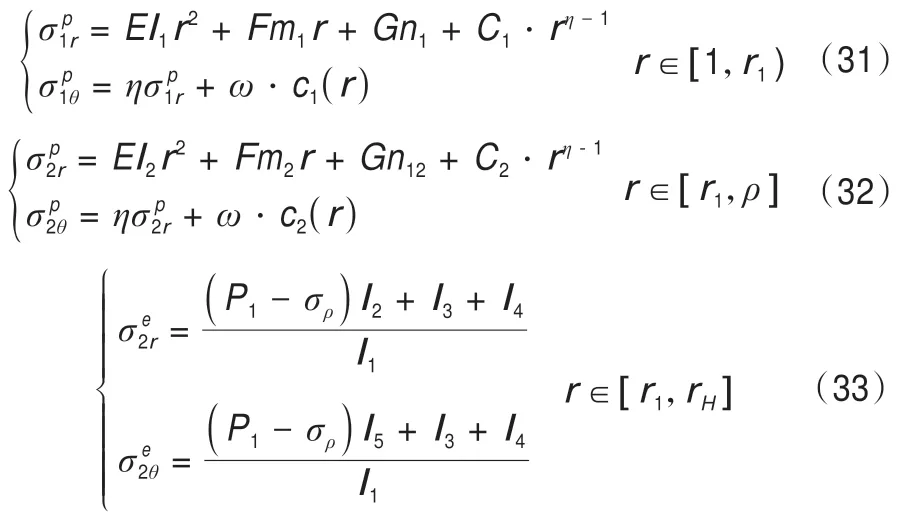
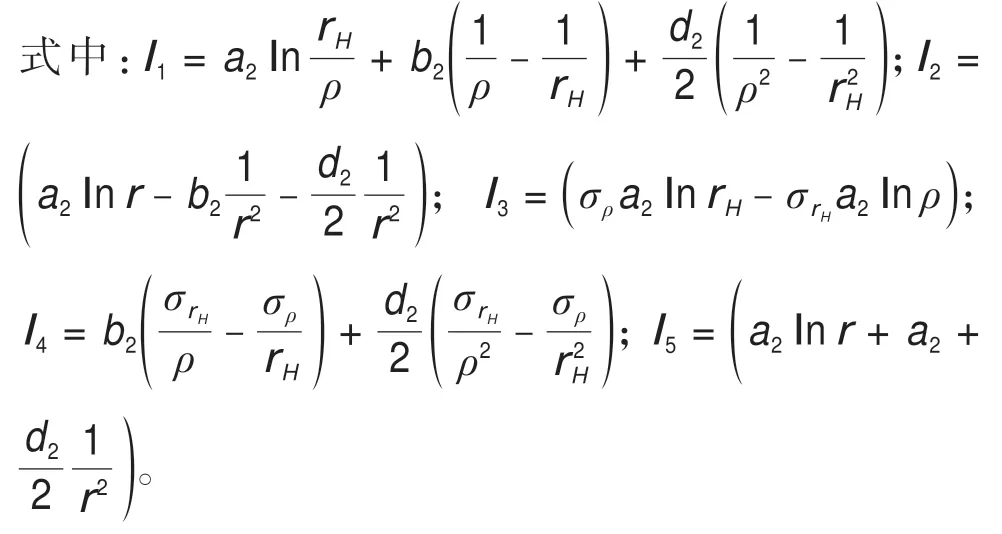
由上述公式可知，當塑性區半徑ρ=1以及ρ=rH時，對應的凍結壁外荷載分別是凍結壁的彈性極限承載力以及塑性極限承載力。

3.4 凍結壁塑性區半徑求解

在r=ρ處，凍結壁應力滿足應力連續條件，即

塑性區半徑可由式（35）、（36）分別聯立（35）求得。

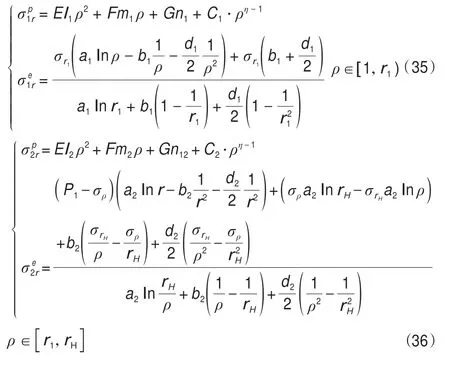
4 工程算例分析

淮南礦區潘一礦中央風井的凍結孔布置方案以及凍土力學參數分別如表2～3所示［25］。

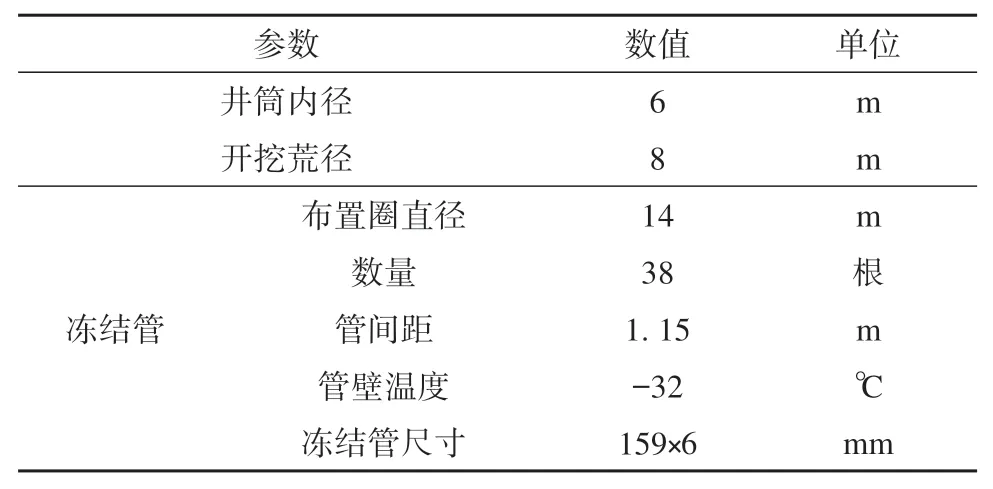
表2 潘一礦中央風井凍結孔設計參數Table 2 Freezing parameters of central wind shaft in Panyi Mine

基于上述參數，通過水熱耦合數值計算模型（該計算模型的合理性已經得到文獻［25］的驗證），采用COMSOL Multiphys數值計算軟件對不同流速條件下凍結壁危險截面的溫度分布規律進行計算，計算結果如圖3所示。

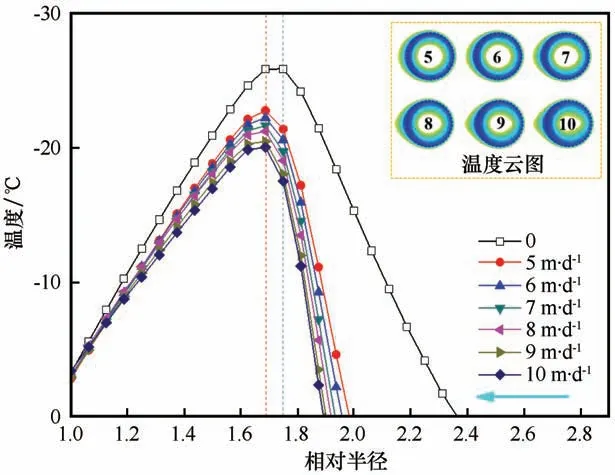
圖3 地下水作用下凍結壁“危險截面”的溫度分布規律Fig.3 The temperature distribution law of the"dangerous section"of the frozen wall under the action of groundwater at different flow rates

對開挖前凍結壁的厚度隨流速的變化規律進行擬合，如圖4所示。

圖4 凍結壁厚度隨地下水流速變化規律的擬合曲線Fig.4 Fitting curve of freezing wall thickness with the change of groundwater velocity

由擬合結果得出凍結壁厚度L與地下水流速V的關系式為：

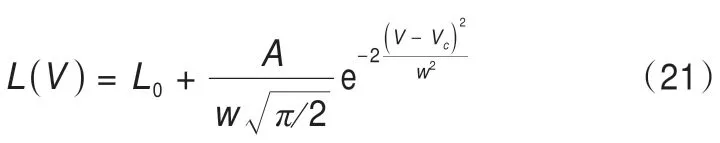
式中：L0、A、w以及Vc為擬合參數。

凍結壁的厚度也可以表示為：

通過數值計算得出凍結壁“危險截面”上溫度曲線的計算參數如表4所示。

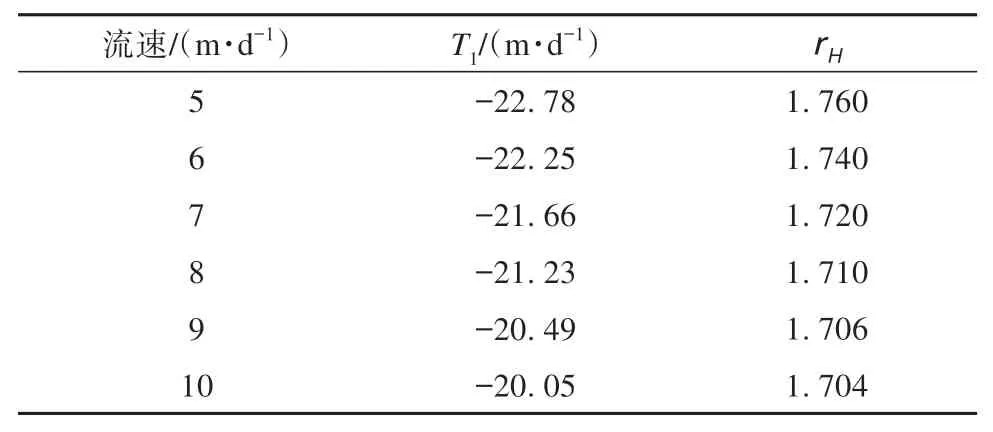
表4 凍結溫度場計算參數Table 4 Calculation parameters of freezing temperature field

將溫度場的計算參數帶入公式（3）可得出不同流速條件下凍結壁危險截面上溫度場計算公式，隨后根據表3中凍土力學參數與溫度的關系，得出凍結壁“危險截面”上彈性模量以及黏聚力隨半徑的變化規律。將彈性模量以及黏聚力帶入對應的應力計算公式，即可得出凍結壁應力計算公式。

表3 凍土力學參數Table 3 Mechanical parameters of frozen soil

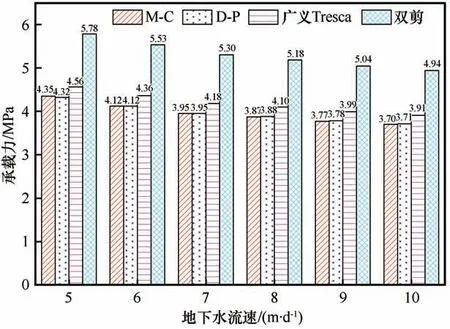
圖6 凍結壁塑性極限承載力計算結果Fig.6 Calculation results of plastic ultimate bearing capacity of frozen wall

不同流速的地下水作用下凍結壁的彈性極限承載力以及塑性極限承載力的計算結果如圖5～6。通過分析可以發現：基于不同屈服準則的凍結壁的承載力的計算結果存在一定的差異，其中基于M-C準則以及D-P準則的計算結果基本一致，基于廣義Tresca準則的結果略大于M-C準則以及D-P準則的計算結果，而基于雙剪強度準則的計算結果則明顯偏大。凍結壁的承載力隨著水流速度的增大而減小，當地下水流速為5 m·d-1時，基于M-C準則、D-P準則、廣義Tresca準則、雙剪準則計算得出的彈性極限承載力以及塑性極限承載力分別為2.480、2.462、2.741、3.202 MPa以及4.349、4.318、4.561、5.779 MPa，當地下水流速增加至10 m·d-1時，對應的彈性極限承載力以及塑性極限承載力降低至2.087、2.085、2.203、2.784 MPa以及3.700、3.707、3.908、4.939 MPa。

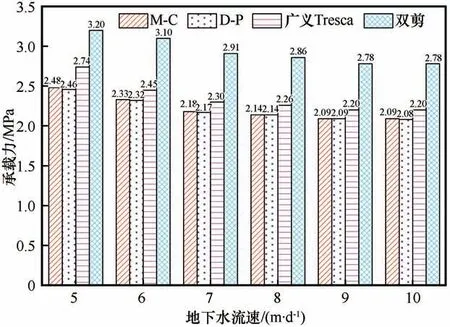
圖5 凍結壁彈性極限承載力計算結果Fig.5 Calculation results of elastic ultimate bearing capacity of frozen wall

彈性極限狀態以及塑性極限狀態下凍結壁的應力分布曲線如圖7～8所示。由于位于凍結壁分區界線（r=1.685）兩側的凍土力學參數存在較大差異，因此位于分界線兩側的凍結壁的應力分布規律也存在較大差異。當凍結壁處于彈性極限狀態時，凍結壁的徑向應力隨著相對半徑r的增大而增大，而環向應力的分布則具有明顯的區域差異性。當r＜1.685時，環向應力曲線呈拋物線形狀，曲線隨相對半徑r的變化較為緩慢；當r＞1.685時，由于地下水的影響該區域凍結壁的厚度較小，溫度變化梯度較大，因此該區域凍結壁的環向應力隨著相對半徑的增加而急劇降低；彈性極限狀態下，凍結壁的環向應力的最大值出現在靠近凍結壁中間的位置。當凍結壁處于塑性極限狀態時，凍結壁的徑向應力隨著相對半徑r的增大而增大，環向應力的分布具有明顯的區域性。當r＜1.685時，環向應力隨著相對半徑r的增大而增大；當r＞1.685時，凍結壁的環向應力隨著相對半徑的增加而急劇降低；塑性極限狀態下，凍結壁的環向應力的最大值出現在凍結壁的分區界線r=1.685處。

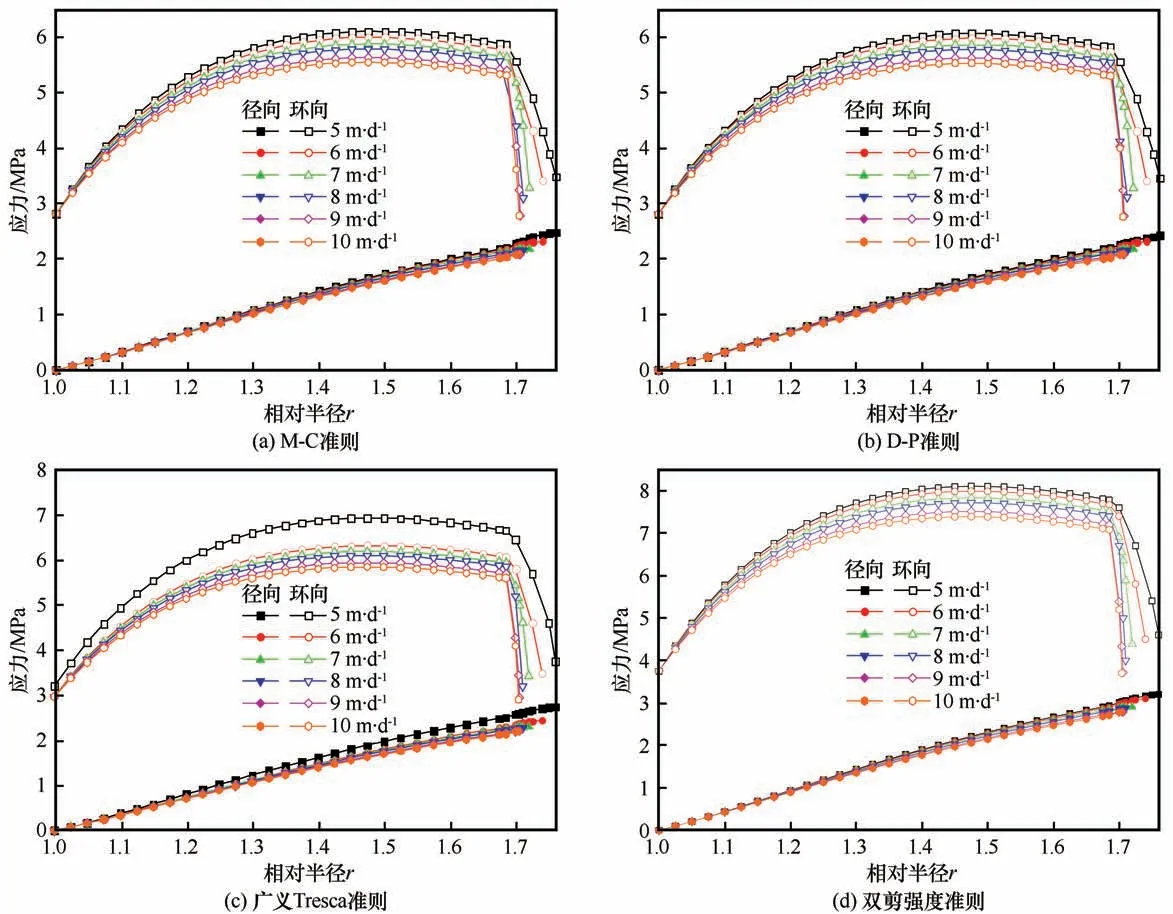
圖7 彈性極限狀態下凍結壁應力分布曲線圖Fig.7 Stress distribution curve of frozen wall under elastic limit state

5 結論與討論

（1）將大流速滲透地層中凍結壁最遲交圈的位置視為“危險截面”，通過分段等效的方法結合溫度特征點，得出該截面的溫度曲線表達式；根據凍土力學參數與凍結溫度的線性關系，將凍結壁視為隨溫度函數變化的非均質材料；分別基于M-C準則、D-P準則、廣義Tresca準則及雙剪強度準則，推導得出滲流場作用下單排管非均質凍結壁應力計算公式。

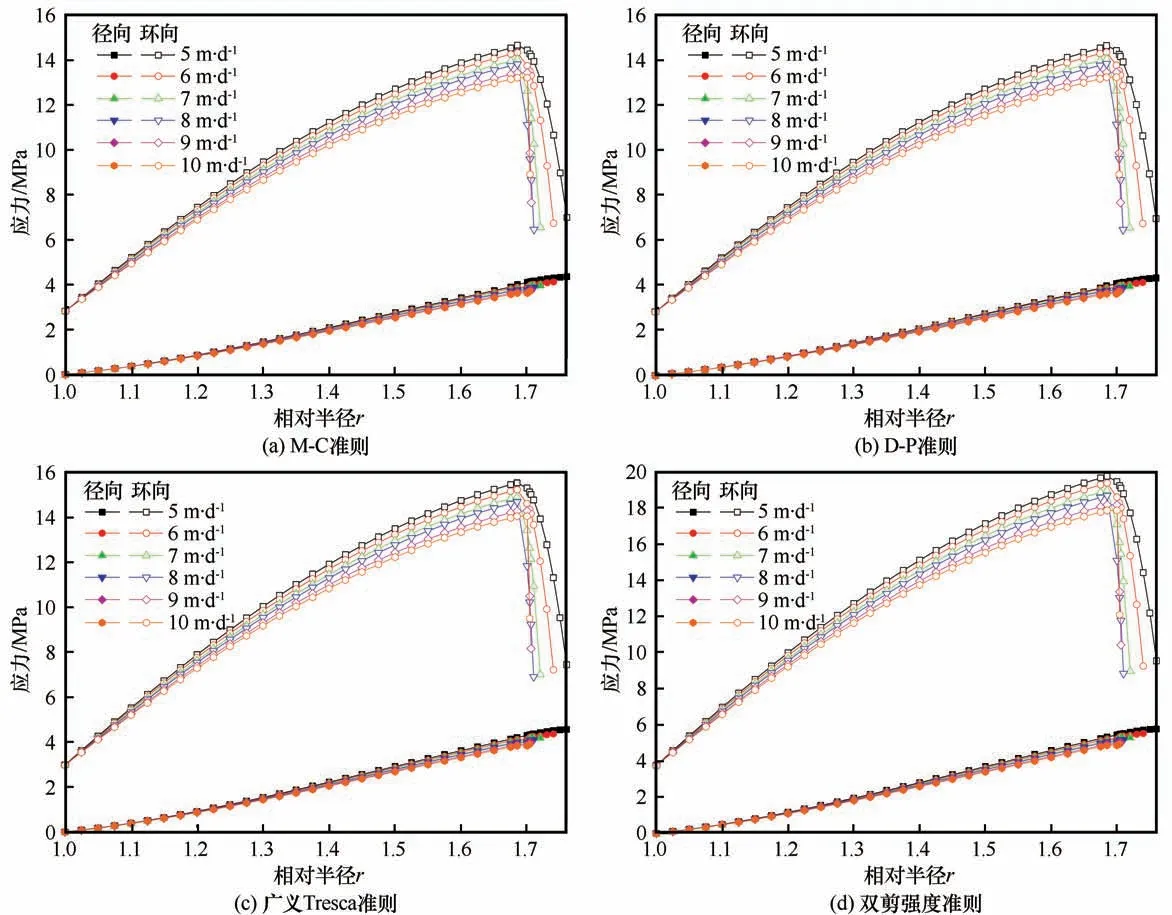
圖8 塑性極限狀態下凍結壁應力分布曲線圖Fig.8 Stress distribution curve of frozen wall under plastic limit state

（2）基于不同屈服準則的凍結壁承載力的計算結果存在一定的差異，其中基于M-C準則以及D-P準則的計算結果基本一致，基于廣義Tresca準則的結果略大于M-C準則以及D-P準則的計算結果，而基于雙剪強度準則的計算結果則明顯偏大。

（3）凍結壁的承載力隨著水流速度的增大而減小，當地下水流速為5 m·d-1時，基于M-C準則、D-P準則、廣義Tresca準則、雙剪準則計算得出的彈性極限承載力以及塑性極限承載力分別為2.480、2.462、2.741、3.202 MPa以及4.349、4.318、4.561、5.779 MPa，當地下水流速增加至10 m·d-1時，對應的彈性極限承載力以及塑性極限承載力降低至2.087、2.085、2.203、2.784 MPa以及3.700、3.707、3.908、4.939 MPa。

（4）當凍結壁處于彈性極限狀態時，凍結壁的徑向應力隨著相對半徑r的增大而增大，環向應力的分布具有明顯的區域差異性。當r＜1.685時，環向應力曲線呈拋物線形狀，應力曲線隨著相對半徑r的變化較為緩慢；當r＞1.685時，由于地下水的影響該區域凍結壁的厚度較小，溫度變化梯度較大，因此該區域凍結壁的環向應力隨著相對半徑的增加而急劇降低；彈性極限狀態下，凍結壁的環向應力的最大值出現在靠近凍結壁中間的位置。

（5）當凍結壁處于塑性極限狀態時，凍結壁的徑向應力隨著相對半徑r的增大而增大，環向應力的分布具有明顯的區域差異性。當r＜1.685時，環向應力隨著相對半徑r的增大而增大；當r＞1.685時，凍結壁的環向應力隨著相對半徑的增加而急劇降低；塑性極限狀態下，凍結壁的環向應力的最大值出現在凍結壁的分區界線r=1.685處。

（6）本研究將定向滲流誘導的非均質凍結壁簡化為受均布荷載、厚度與危險截面處凍結壁相等的“厚壁圓筒”，并基于四種凍土強度準則對不同流速條件下凍結壁的力學特性進行了計算分析，所得出的結果反映了凍結壁最危險狀態下的力學特性，能夠為大流速滲透地層凍結壁的設計提供一定的參考。但是，受理論解析方法的限制，該模型僅能反映進入穩態的凍結壁的力學特性，沒有考慮水-熱-力耦合作用，我們將在后續的研究中采用數值計算的方法對該問題展開進一步深入的探索。