采煤機(jī)滾筒調(diào)高智能化控制系統(tǒng)優(yōu)化設(shè)計(jì)
范四立
(東莞職業(yè)技術(shù)學(xué)院機(jī)電工程學(xué)院,廣東東莞 523808)
0 前言
采煤機(jī)是煤礦井下綜采工作面重要設(shè)備之一,其智能化水平是衡量綜采工作面智能化水平的重要參考,而采煤機(jī)滾筒智能調(diào)高是完成采煤機(jī)智能化的重要決策。采煤機(jī)滾筒精確、平穩(wěn)、快速智能調(diào)高是目前國內(nèi)外學(xué)者關(guān)注的熱議話題。耿秀明通過傳遞函數(shù)求解了調(diào)高系統(tǒng)狀態(tài)空間方程,并在該系統(tǒng)控制器設(shè)計(jì)中引入了滑模變結(jié)構(gòu)控制。劉芳璇等基于AFSA-ACA自適應(yīng)模糊滑模對滾筒液壓調(diào)高進(jìn)行了精確控制。李雪梅利用滑模變結(jié)構(gòu)控制理論對采煤機(jī)滾筒系統(tǒng)控制器進(jìn)行了設(shè)計(jì)與研究,給出了變速趨近律的滑模變結(jié)構(gòu)控制方法優(yōu)勢。
目前,螢火蟲控制算法大多被用于解決連續(xù)型最優(yōu)化問題,具有較優(yōu)性能。杜鵬楨等研究出一種基于改進(jìn)螢火蟲算法的路徑規(guī)劃方法,并利用大量仿真試驗(yàn)及實(shí)際試驗(yàn)驗(yàn)證其可行性和有效性。毛君等人基于新型螢火蟲算法對機(jī)尾PID控制策略進(jìn)行了優(yōu)化設(shè)計(jì),對標(biāo)準(zhǔn)螢火蟲算法的動(dòng)態(tài)決策域更新系數(shù)進(jìn)行了改進(jìn)。左仲亮等設(shè)計(jì)了改進(jìn)的動(dòng)態(tài)步長螢火蟲優(yōu)化算法,該算法在尋優(yōu)初期以相對較大的步長進(jìn)行搜索,其全局尋優(yōu)能力較強(qiáng)。
采煤機(jī)工作環(huán)境惡劣且復(fù)雜,而目前針對采煤機(jī)滾筒調(diào)高的研究主要為系統(tǒng)響應(yīng)性能研究,對系統(tǒng)抗干擾性能的研究較少。針對采煤機(jī)滾筒調(diào)高智能化要求,本文作者對螢火蟲算法進(jìn)行改進(jìn)設(shè)計(jì)。對采煤機(jī)滾筒調(diào)高智能化控制系統(tǒng)進(jìn)行數(shù)學(xué)建模,采用改進(jìn)的螢火蟲算法對調(diào)高系統(tǒng)PID控制器參數(shù)進(jìn)行尋優(yōu)設(shè)計(jì),并建立滾筒調(diào)高智能化控制系統(tǒng)Simulink仿真模型,給出改進(jìn)和基本螢火蟲算法的滾筒調(diào)高系統(tǒng)優(yōu)化效果對比曲線。
1 螢火蟲算法改進(jìn)
圖1所示為基本螢火蟲算法控制邏輯,采用的是固定步長的方式。由于固定步長會(huì)使算法陷入局部最優(yōu),不便于在全局內(nèi)搜索最優(yōu)解,故文中通過模糊算法將固定步長設(shè)計(jì)為自適應(yīng)步長,以提高全局搜索能力。

圖1 基本螢火蟲算法控制邏輯
表1所示為模糊控制規(guī)則。模糊控制器輸入變量分別為算法當(dāng)次尋優(yōu)結(jié)果與上次尋優(yōu)結(jié)果誤差及其偏差變化率;輸出變量為自適應(yīng)步長變化量Δ。表1中:NB為負(fù)大、NM為負(fù)中、NS為負(fù)小、ZO為零、PS為正小、PM為正中、PB為正大。
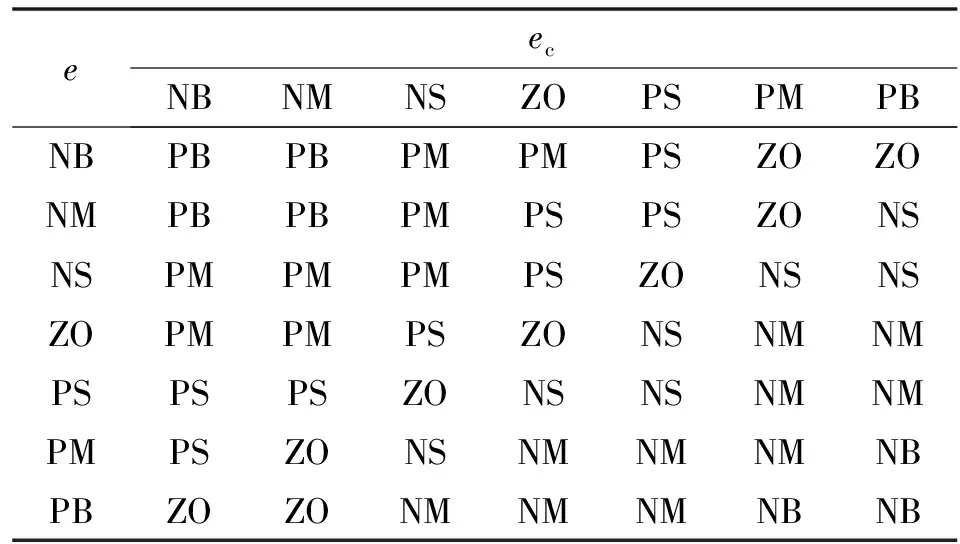
表1 Δs模糊控制規(guī)則
為增加算法優(yōu)化初期收斂速度,采取擴(kuò)大螢火蟲的動(dòng)態(tài)決策半徑方法,通過重新定義決策域更新系數(shù),如方程(1)所示:
=·
(1)
式中:為指數(shù)分布。
2 滾筒調(diào)高智能化控制系統(tǒng)優(yōu)化
2.1 調(diào)高智能化控制系統(tǒng)數(shù)學(xué)建模
圖2所示為采煤機(jī)滾筒調(diào)高智能化控制系統(tǒng)原理簡圖。系統(tǒng)主要元件有齒輪泵、控制換向閥、液壓缸及控制器。其工作原理可簡述為:位移傳感器采集液壓缸活塞桿實(shí)時(shí)位移信號(hào)并傳輸給上位機(jī),上位機(jī)對誤差信號(hào)進(jìn)行處理以進(jìn)一步輸出控制信號(hào),控制信號(hào)經(jīng)放大器放大后調(diào)節(jié)比例電磁鐵動(dòng)作,進(jìn)而控制換向閥主閥芯動(dòng)作,實(shí)時(shí)調(diào)整活塞桿位移,從而實(shí)現(xiàn)滾筒高度智能化調(diào)整。
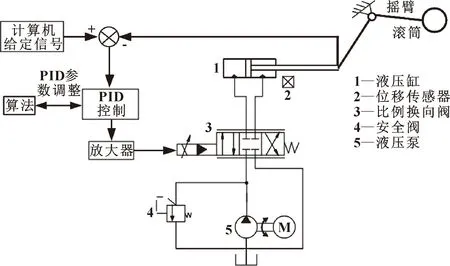
圖2 采煤機(jī)滾筒調(diào)高智能化控制系統(tǒng)
由系統(tǒng)工作原理可以看出,該系統(tǒng)為閥控缸系統(tǒng),閥控缸系統(tǒng)數(shù)學(xué)模型由3個(gè)初始方程組成。
控制換向閥的線性負(fù)載流量數(shù)學(xué)模型用式(2)表示:
==-
(2)
式中:為流量增益,m/s;為閥芯位移,m;為流量壓力系數(shù),m·Pa/s;為液壓缸壓力,Pa。
調(diào)高缸輸入輸出流量連續(xù)性方程用式(3)表示:

(3)
式中:為活塞有效工作面積,m;為有效體積彈性模量,N/m;為活塞位移,m;為液壓缸總泄漏系數(shù),m·Pa/s;為進(jìn)油腔容積,m。
力平衡方程可由式(4)表示:
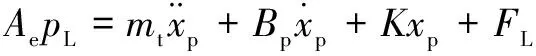
(4)
式中:為活塞及負(fù)載折算到活塞上的總質(zhì)量,kg;為活塞及負(fù)載的黏性阻尼系數(shù),kg/s;為干擾負(fù)載,N;為負(fù)載彈簧剛度,N/m。
對方程(2)、(3)和(4)進(jìn)行拉氏變換,基于采煤機(jī)滾筒實(shí)際工況獲得液壓缸活塞桿輸出位移如下:

(5)
通過方程(5)進(jìn)一步可獲得活塞桿位移對閥芯位移的傳遞函數(shù),如方程(6)所示:

(6)
式中:為液壓固有頻率,rad/s;為液壓阻尼比;為總流量-壓力系數(shù)。
因此,可得到調(diào)高缸活塞位移(負(fù)載)的方程為
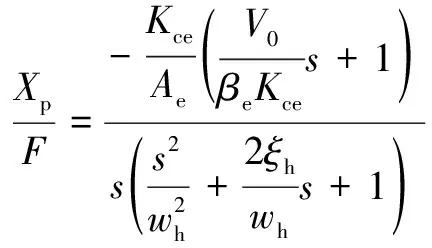
(7)
比例換向閥數(shù)學(xué)模型為

(8)
式中:為閥芯位移,m;為閥芯位移與電流增益系數(shù),L/(min·A)。
2.2 調(diào)高智能化控制器優(yōu)化
采煤機(jī)滾筒調(diào)高智能化控制系統(tǒng)采用增量式PID控制器,便于實(shí)現(xiàn)PLC控制。其參數(shù)調(diào)整只和最近3次采樣有關(guān),更適合控制液壓系統(tǒng)。
增量式PID控制器輸出如下:
()=(-1)+Δ()
(9)
Δ()=[()-(-1)]+()+
[()-2(-1)+(-2)]
(10)
式中:、和分別為PID的3個(gè)參數(shù);Δ()為控制器第次的輸出量的增量;()和(-1)分別為第次和第-1次PID控制器的輸出;()、(-1)和(-2)分別為第次、-1次和-2次的活塞桿位移差。
圖3所示為改進(jìn)的螢火蟲算法優(yōu)化的PID控制器結(jié)構(gòu)框圖。

圖3 改進(jìn)的螢火蟲算法優(yōu)化的PID控制器
圖4所示為改進(jìn)的螢火蟲算法優(yōu)化PID控制器的流程圖。采用ITAE作為評價(jià)指標(biāo)函數(shù),如式(11)所示:

圖4 改進(jìn)的螢火蟲算法優(yōu)化PID控制器的流程
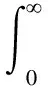
(11)
在MATLAB中進(jìn)行程序編寫,部分程序步驟如下:
步驟(1),初始化螢火蟲算法參數(shù);
步驟(2),計(jì)算各螢火蟲的亮度并排序得到亮度最大的螢火蟲位置;
步驟(3),判斷迭代是否結(jié)束;達(dá)到最大迭代次數(shù),則進(jìn)行步驟(4),否則進(jìn)行步驟(5);
步驟(4),輸出亮度最大的螢火蟲位置及其亮度;
步驟(5),根據(jù)式(3)更新螢火蟲的位置,對處在最佳位置的螢火蟲進(jìn)行隨機(jī)擾動(dòng),搜索次數(shù)增加1,執(zhí)行步驟(2),進(jìn)行下一次搜索。
參數(shù)設(shè)置如下:設(shè)置螢火蟲種群規(guī)模為30,初始熒光素為5,熒光素濃度揮發(fā)速度系數(shù)為0.4,螢火蟲個(gè)體更新速度系數(shù)為0.6,決策域范圍更新系數(shù)初始值為0.08,螢火蟲的初始步長(0)為0.03,最大迭代次數(shù)為100,最小移動(dòng)步長0.000 1,最大移動(dòng)步長為1。
通過螢火蟲算法改進(jìn)尋優(yōu)后的PID控制器參數(shù)為=24.308 1、=0.915 7和=1.480 3。
3 系統(tǒng)仿真結(jié)果及分析
圖5所示為利用Simulink搭建的采煤機(jī)滾筒調(diào)高智能化控制系統(tǒng)仿真模型,系統(tǒng)仿真參數(shù)設(shè)置如表2所示。
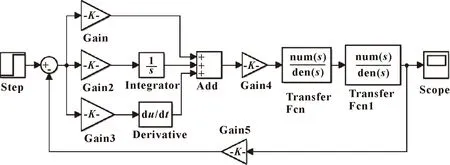
圖5 滾筒調(diào)高智能化控制系統(tǒng)Simulink仿真模型

表2 仿真參數(shù)
仿真對比改進(jìn)和基本螢火蟲算法優(yōu)化的PID控制器,給系統(tǒng)分別施加階躍和斜坡信號(hào),幅值為1 m,得到改進(jìn)和基本螢火蟲算法仿真結(jié)果對比如圖6—圖7所示。

圖6 階躍響應(yīng)曲線對比(局部) 圖7 斜坡響應(yīng)曲線對比(局部)
由圖6可得:階躍響應(yīng)下,與基本螢火蟲算法相比,改進(jìn)螢火蟲算法優(yōu)化的PID控制器使調(diào)高系統(tǒng)超調(diào)量減小了21.6%,調(diào)整時(shí)間下降了18.1%,穩(wěn)態(tài)誤差降低了9.7%。
由圖7可得:斜坡響應(yīng)下,與基本螢火蟲算法相比,改進(jìn)螢火蟲算法優(yōu)化的PID控制器使調(diào)高系統(tǒng)超調(diào)量減小了38.4%,調(diào)整時(shí)間下降了22.8%,穩(wěn)態(tài)誤差降低了4.6%。
為驗(yàn)證加入改進(jìn)螢火蟲算法優(yōu)化的PID控制器的系統(tǒng)魯棒性能是否得到提高,對穩(wěn)態(tài)系統(tǒng)施加各種干擾,查看系統(tǒng)對干擾的抗干擾能力和抑制力度。
選取3種類型的信號(hào)干擾:脈沖信號(hào)干擾、階躍信號(hào)干擾和隨機(jī)信號(hào)干擾,系統(tǒng)抗干擾能力仿真曲線如圖8—圖10所示。
圖8所示為系統(tǒng)穩(wěn)態(tài)時(shí)對系統(tǒng)加入幅值為0.1 m、周期為1 s的脈沖干擾信號(hào)的局部響應(yīng)對比曲線。可知:與基本螢火蟲算法相比,改進(jìn)螢火蟲算法優(yōu)化后的PID控制系統(tǒng)的響應(yīng)峰值減小了21.9%,調(diào)整時(shí)間下降了10.7%。
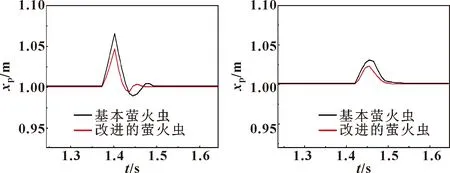
圖8 脈沖干擾響應(yīng)曲線(局部) 圖9 階躍干擾響應(yīng)曲線(局部)
圖9所示為系統(tǒng)穩(wěn)態(tài)時(shí)對系統(tǒng)加入幅值為0.05 m的階躍干擾信號(hào)的響應(yīng)對比曲線。可知:與基本螢火蟲算法相比,改進(jìn)螢火蟲算法優(yōu)化的PID控制器系統(tǒng)的超調(diào)量減小了33.2%,調(diào)整時(shí)間下降了15.07%。
圖10所示為系統(tǒng)穩(wěn)態(tài)時(shí)對系統(tǒng)加入幅值為0.01 m、頻率為10 Hz的隨機(jī)干擾信號(hào)的響應(yīng)對比曲線。可知:與基本螢火蟲算法相比,改進(jìn)螢火蟲算法優(yōu)化的PID控制系統(tǒng)的系統(tǒng)響應(yīng)曲線波蕩范圍減小了40.1%。

圖10 隨機(jī)干擾響應(yīng)對比曲線(局部)
由此可得:對滾筒調(diào)高智能化系統(tǒng)施加階躍、斜坡、不同類型干擾信號(hào)時(shí),當(dāng)加入改進(jìn)螢火蟲算法優(yōu)化的PID控制器后,其響應(yīng)性能和抗干擾性能得到大幅度提高,研究結(jié)果可在一定程度上為采煤機(jī)滾筒智能化發(fā)展提供參考。
4 結(jié)論
為提高采煤機(jī)滾筒調(diào)高智能化控制精度,對基本螢火蟲算法進(jìn)行改進(jìn)。對采煤機(jī)滾筒調(diào)高智能化控制系統(tǒng)進(jìn)行數(shù)學(xué)建模,利用改進(jìn)的螢火蟲算法對滾筒控制系統(tǒng)PID參數(shù)進(jìn)行尋優(yōu),并搭建了滾筒調(diào)高智能化控制系統(tǒng)仿真模型。對改進(jìn)和基本螢火蟲算法系統(tǒng)的效果進(jìn)行對比分析。對滾筒調(diào)高控制系統(tǒng)加入改進(jìn)螢火蟲算法優(yōu)化的PID控制器后,系統(tǒng)響應(yīng)性能和抗干擾性能得到較大改善和提高,主要得到以下結(jié)論:
(1)階躍信號(hào)下,優(yōu)化后的系統(tǒng)超調(diào)量、調(diào)整時(shí)間和穩(wěn)態(tài)誤差分別減小21.6%、18.1%和9.7%;
(2)斜坡信號(hào)下,優(yōu)化后的系統(tǒng)超調(diào)量、調(diào)整時(shí)間和穩(wěn)態(tài)誤差分別減小38.4%、22.8%和4.6%;
(3)脈沖干擾信號(hào)下,優(yōu)化后的系統(tǒng)超調(diào)量和調(diào)整時(shí)間分別減小21.9%和10.7%;
(4)階躍干擾信號(hào)下,優(yōu)化后的系統(tǒng)超調(diào)量和調(diào)整時(shí)間分別減小33.2%和15.07%;
(5)隨機(jī)干擾信號(hào)下,優(yōu)化后的系統(tǒng)響應(yīng)曲線波蕩范圍減小40.1%。

