數學思想、數學活動與小學數學教學研究

周安艷 江蘇省泗洪姜堰實驗學校

課程標準作為指導義務教育階段教育實踐工作的綱領性文件，始終根據社會、國家發展需要及人才成長需要調整教育工作目標。從最新的課程改革成果來看，針對小學階段數學學科的教育，要求繼承“雙基”發展學生“四基”，從而使小學數學在培養學生分析與解決問題能力的基礎上，關注學生發現與提出問題能力的發展。因而在教學過程中數學思想、數學活動及教學實踐活動均需做出適時的調整。本文中，通過對小學數學思想及數學活動的分析，探究實現數學思想、數學活動與數學教學實踐相結合的策略。

一、數學思想與數學活動分析

新課標中強調，學生綜合素質的培養是教學的主要目標。數學活動的意義是將學生的實際生活與教學目標結合，在提高數學學習趣味性的同時，培養學生的自主能力，激發學生主動學習的意向，讓他們可以靈活地掌握與使用自己學習到的知識。可以說，在小學數學教學中運用數學活動，不僅能夠提高小學生的學習效果、培養綜合素質，也是提高小學數學教學水平與質量的重要方式。

數學是一門具有較強邏輯性的學科，小學是奠定學生數學基礎的階段，順利進行課堂教學需要教師針對教學內容與學生發展需要展開科學設計，通過教學過程將數學思想傳遞。因此，數學思想即通過反復的數學實踐總結出來的能夠對學生在解決數學問題的過程中分析問題、思考問題、判斷問題、推理問題有所幫助的思想，而從其對學生的作用來看，其本質上也屬于一種能力，該項能力強調學生學習的自主性與獨立性。目前，在小學階段，滲透的數學思想主要有化歸思想、分類思想、總結思想、類比思想、數形結合思想、單位思想、符號化思想。

與數學思想相比，對數學活動的理解則更為簡單，從字面則可明確數學活動是數學教學活動，數學教學過程中，以發生環境劃分主要有兩種形式，分別為課內活動與課外活動，但兩種形式的活動均具有相同的目的與價值，即通過數學活動引導學生學習知識、了解知識、掌握數學技能、構建完善的知識體系。因此，數學活動是構建學生與問題之間關鍵的橋梁，是學生探索數學世界的契機。

二、數學思想、數學活動與數學教學結合的策略

（一）明確數學思想、深入滲透數學思想

數學思想的形成需經過反復的數學實踐，其本身是數學領域的精華，是對數學知識的高度總結與概括。為發展學生的數學思維與意識，應將數學思想的滲透貫穿數學教學始終。在展開課堂教學活動時，教師應有目的性地分析教材，總結各部分知識涉及的數學思想，提煉數學思想的具體特征，在數學教學中重點講解，使數學思想在學生解決數學問題時切實發揮作用。具體來講，則要求教師在課前準備環節，深入展開教材內容歸納、分析，總結數學思想內容，結合教學內容、例題選擇，以便于學生接受與理解的方式滲透數學思想，并搭配例題對思想的具體運用展開分析，要求既能概括所學知識，又能夠讓學生理解知識重點。同時，數學教學中，多數教師均喜歡通過題海戰術幫助學生鞏固知識，但反復的機械式訓練并不利于學生理解數學思想，建議始終將數學思想融合到教學實踐活動中，如探究環節，指導學生利用數學思想思考出探究方法，從而解決實際問題。

例如，動物園中舉行跳躍比賽，狐貍、黃鼠狼報名參加，其中狐貍每次跳躍米、黃鼠狼每次跳躍米，每秒鐘完成一次跳躍，但跳躍過程中在米處設置陷阱，問：狐貍與黃鼠狼誰先遇到陷阱？未掉入陷阱者總共跳躍多少米？很多學生在遇到問題時，因題中存在分數、計算難度大而產生困惑，但通過分析發現，掉入陷阱者，其跳躍距離是每次跳躍的距離的整數倍，也是米的整數倍，即可以說是的最小公倍數或的最小公倍數。因此，分別計算出兩種動物跳躍了幾次，則可確定誰掉進陷阱與跳躍的距離。該問題的思考中，是將實際問題通過轉化按照數學中最小公倍數的知識進行解決，其中涉及化歸思想，實現正確的轉化則可直接找到解決問題的突破口。

（二）綜合數學思想與數學活動實踐

課堂教學不僅是傳遞知識的活動，也是鍛煉學生能力的活動，從上述內容可知，學會數學思想的靈活運用本身也是對學生能力的考查，因此，在教學過程中，實現數學思想與數學活動實踐的綜合，不僅可以讓學生理解數學思想的實際應用價值，也是通過數學活動鍛煉學生的數學思想運用能力的重要契機。因此，在這個過程中，教師需要適當地給予學生學習主動權，如通過自主探究、自主構建知識體系等方式，使學生更深刻地理解數學思想，真正地感受到數學活動的樂趣與意義所在。但需要注意，考慮到小學階段學生的年齡與認知水平特性，建議在高段數學教學中綜合數學思想與數學活動實踐，避免過早給學生學習增加難度，影響學生的信心。

例如，在數列知識教學過程中，數列是強化小學生數學思維訓練的類型題，小學階段常見的數列多為等差數列、等比數列，數列計算有直接公式，如數列和公式為］、項 目 公 式 為，很多學生將公式熟記于心，但實際應用時，無法準確確定首項、末項、公差等，這就表明學生所掌握的數學思想與數學活動實踐脫節。在例題中，與單獨正整數數列（如圖1 所示）求和存在差異，其分子與分母之間有著特殊的關系，需要經過轉化，尋找規律，合理套入數列公式，經過轉化發現分母的規律：2=1×2，6=2×3，12=3×4，20=4×5，…，380=19×20，通過拆分可將數列轉化成的形式，從而得到式子：。整個計算過程中，需要學生靈活運用符號思想、集合思想、對應思想等，這樣的方式可將數學思想與數學活動實踐結合起來，幫助學生利用實踐理解數學思想的運用。

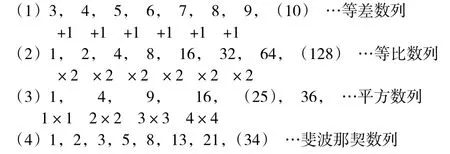
圖1 常見正整數數列

（三）重視數學思想與活動經驗總結

在完成課堂教學后，教師需要對課堂中教授的知識進行歸納總結。新課標要求教師在歸納總結課堂教學的同時，要引導學生對學習的知識進行總結，在這個過程中發現學生的問題并及時糾正，引導學生采用正確的思路，為靈活學習打好基礎。若在教學過程中真正地通過實踐活動培養學生的數學思想，有必要在活動后總結思想與經驗，對思想運用過程中涉及的重點進行歸納，提煉出涉及的數學思想，進一步強調，幫助學生理解，以期實現解決問題中的靈活運用。

三、結束語

綜上所述，數學思想、數學活動與數學教育之間的有機結合是實現新課標關于發展小學生數學核心素養目標的必經路徑，其滿足新課標對教學實踐的指導與要求，在提升與發展學生綜合能力上有著無可比擬的優越性。因此，小學數學教師應重視教學過程中結合數學活動滲透數學思想，在實踐中幫助學生深刻理解數學思想的內涵、運用的方式，從而形成數學思想、發展數學核心素養。