基于并聯機構的船舶運動模擬控制器設計與仿真

姚濤，張鰻，王志華，高琳

(1.河北工業大學機械工程學院,天津 300401；2.國家技術創新方法與實施工具工程技術研究中心,天津 300401；3.河北工業大學電氣工程學院，天津 300130)

0 前言

近年來，隨著海洋與軍事工程的發展，船舶的動態問題及船用設備的可靠性問題引起國內外學者的關注。為了降低海試成本，國內外相關公司和研究機構設計了不同結構的船舶運動模擬器，以便模擬不同海況下船體的運動情況，測試船用儀器設備的可靠性，同時可用于研究人體對船舶運動的反應情況。荷蘭國家應用科學研究院采用液壓驅動方式設計了一種三自由度運動模擬器，用于人體運動病理研究，該模擬器垂蕩幅值可達1 m，縱搖運動最大偏角為40°，橫搖運動最大偏角為30°。美國海軍Carderock作戰中心研制了電液混合驅動的兩自由度(橫搖和縱搖)運動模擬器，可模擬7級海況。美國August公司基于六自由度并聯機構研制了一種運動模擬平臺，該平臺主要由伺服液壓系統、運動參數檢測傳感器、信號分析和處理系統、計算機系統等組成，用于海上作業人員的訓練和船舶儀器的測試。加拿大船舶運動模擬中心研制了六自由度船舶運動模擬器，用于測試船員的暈船癥狀。

基于并聯機構的運動模擬器能較好地體現船舶在波浪中的運動特性。在國內，韓俊偉和姜洪洲研究了用于航海模擬的六自由度并聯機器人，并且實現了機器人的自主操縱功能。陳曉江提出了將Bayes診斷法應用于六自由度艦船模擬搖擺平臺，完成了位姿誤差診斷實驗，并采用誤差放大因子法進行相關的誤差分析。邢繼峰等以六自由度潛艇操縱模擬器為例，分析了運動平臺在各種作動器下的位移、速度和加速度。楊鵬針對船舶六自由度運動模擬臺的特點，提出了采用同步控制與關節控制相結合的復合控制策略，以達到消除負載擾動，提高多通道執行機構的同步性，獲得良好的運動性能和跟蹤目標等目的。王崇建立了船舶在波浪作用下的橫搖和縱搖運動虛擬樣機模型，應用模糊控制器對船舶的姿態進行了有效控制。2009年，臺灣船舶設計開發中心自行研制了基于六自由度機械運動平臺的微機版船舶操縱模擬器。呂鋒、李盈采用模塊化的Stewart機構與基于EMC2控制器的開放式控制系統相結合的方法實現運動平臺仿真，并設計了六自由度并聯船舶運動模擬器的EMC2和ADRC控制器，基于三維立體圖形分析法整定了參數。黨嬰龍、魏世偉和宋維斌均針對波浪運動模擬器進行了建模與控制策略研究。夏雨、楊軍宏針對船舶運動模擬器進行了動力學建模與動感模擬算法研究。

1 機構運動逆解算法及仿真模型

1.1 位置逆解

典型的Stewart并聯機構主要由動平臺(上平臺)、靜平臺(下平臺)、液壓驅動支鏈、連接鉸組成，如圖1所示。在驅動支鏈的主動力作用下，動平臺可實現空間內6個自由度的運動，其位姿狀態可用來描述船舶在波浪中的運動狀態。圖2所示為Stewart并聯機構原理簡圖，靜坐標系-固定在靜平臺中，動坐標系′-′′′固定在動平臺中心處。靜坐標系原點與靜平臺的質心重合，動坐標系原點與動平臺的質心重合。、、…、、、、…、表示連接動靜平臺鉸點。6條支鏈伸縮桿分別表示為、、、、、。靜坐標系的鉸鏈連接半徑為0.28 m，動靜平臺相鄰支鏈最小夾角均為30°。處于最小夾角的相鄰兩個鉸鏈為一組，每組間隔120°均布于動靜平臺上。

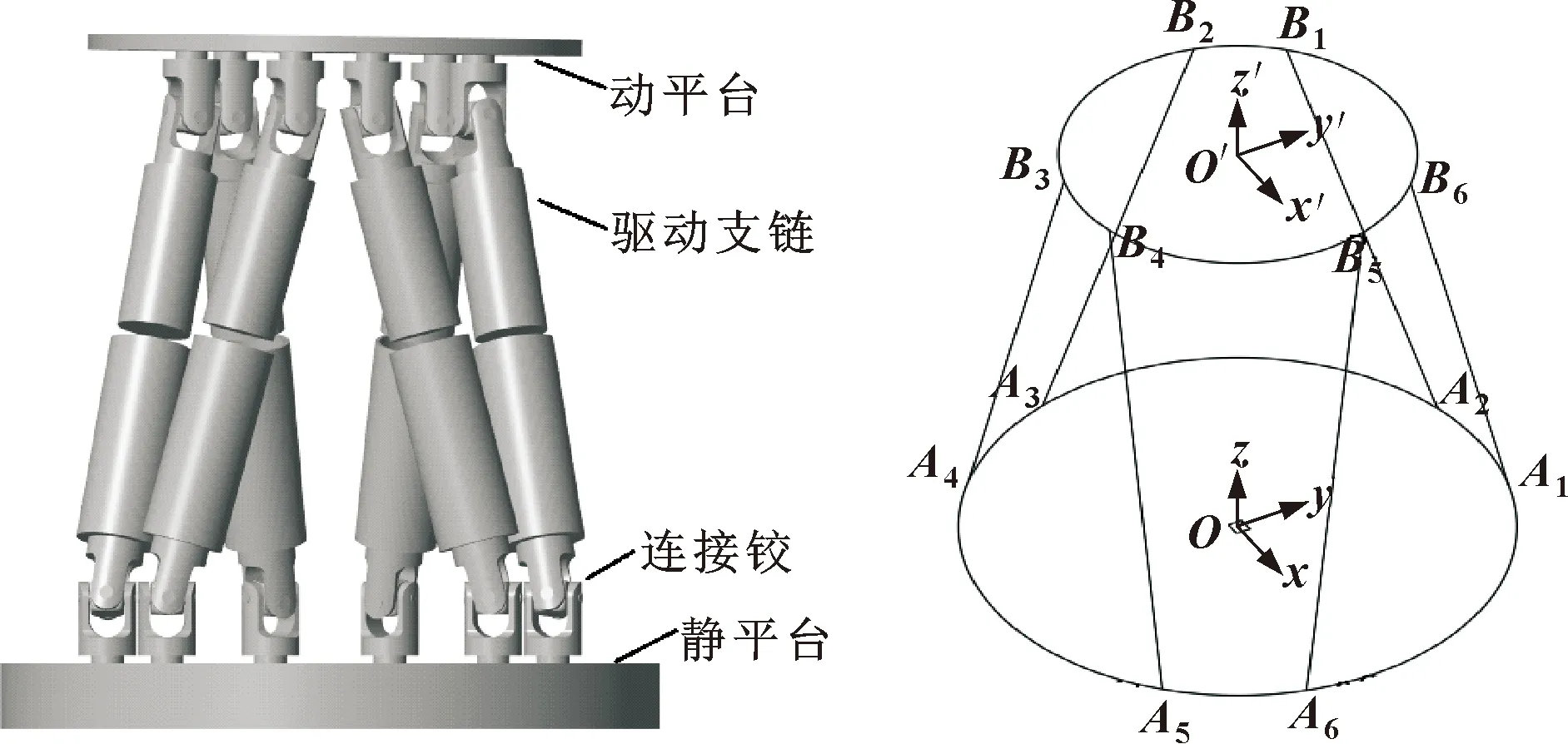
圖1 Stewart并聯機構物理模型 圖2 Stewart并聯機構原理

由空間矢量關系可得各支鏈桿長表達式：

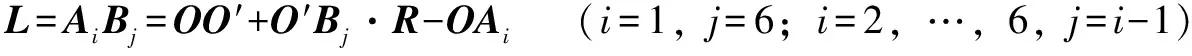
(1)

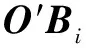
現假定機構初始幾何參數：==π/12，=0.633 61 m，=0.28 m，=0.18 m。其中:為靜平臺鉸接點與軸的初始夾角，為動平臺鉸接點與′′的初始夾角。支鏈初始位置定義為下平臺、、鉸接點的分布角；定義為靜平臺、、鉸接點的分布角。靜平臺各分布角的表達式為

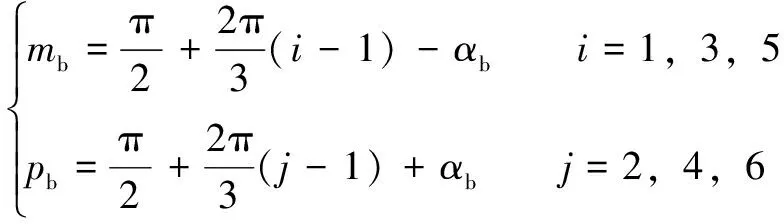
(2)

連接靜平臺各鉸接點在靜坐標系中的坐標值為

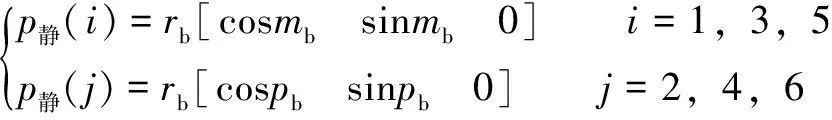
(3)

定義為動平臺、、鉸接點的分布角，定義為動平臺、、鉸接點的分布角，則：

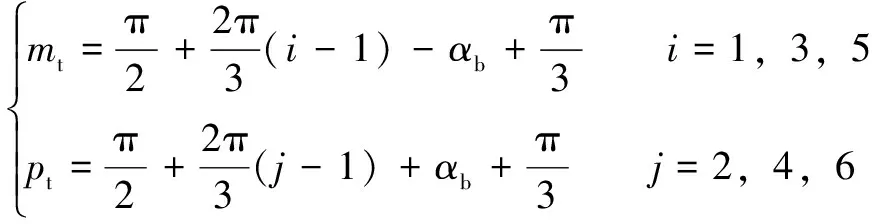
(4)

動平臺各鉸接點相對于靜坐標系的坐標值為

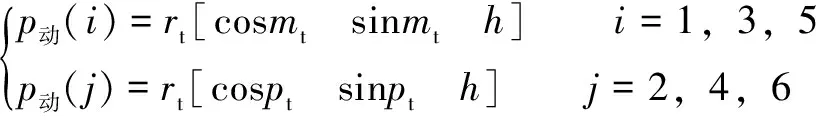
(5)

動坐標系中的任意向量′，均可以通過坐標轉換變換為相對于靜坐標系的向量，轉換關系表達式表示為

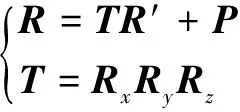
(6)

=[]

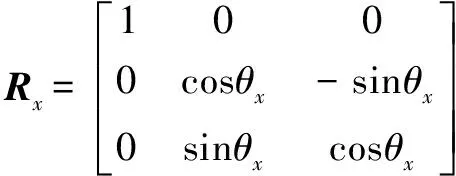
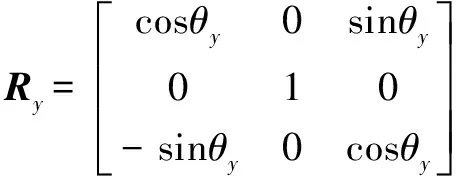
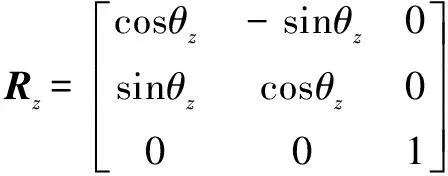
(7)

由依次繞、、軸旋轉定義的旋轉矩陣、、相乘得到。其中，、、分別表示動平臺翻滾角、俯仰角和偏轉角；為動平臺原點相對于靜坐標系中的位置矢量。基于空間矢量關系可獲得動靜平臺鉸接點、(=1,2,3,4,5,6)相對于靜坐標系的坐標值。每2個鉸鏈與中心連線的夾角為30°，6個鉸鏈分為3組按120°分布，即、2個矩陣，2個矩陣均為6×3階矩陣，每一行表示相應行數的鉸鏈連接點的坐標值。各個支鏈的長度為

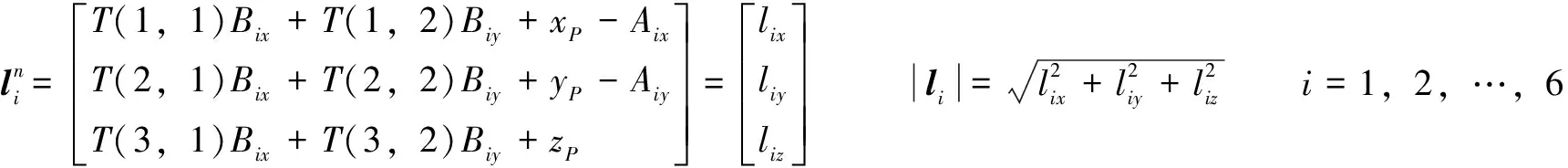
(8)

通過式(8)可以得到動平臺相應位姿以及各個支鏈的長度，計算出各支鏈的伸縮量。將伸縮量作為桿的驅動裝置的主動輸入信號，可實現驅動系統獲得動平臺所期望的位姿。

1.2 系統仿真模型

基于上述算法，應用MATLAB/Simulink仿真平臺建立運動學逆解模型，輸入動平臺期望位姿信號[,,,,,]，可以獲得對應驅動支鏈的運動位移、速度等運動學相關參數。其中，、、表示動平臺的期望姿態角，、、表示動平臺的期望位置。

圖3所示為基于MATLAB/SimMechanics建立的并聯機構模型。其中，S-PS子模塊是將Simulink中的信號轉換為實體所需要的PS信號；PS-S模塊是將實體的PS信號轉換為Simulink所需的信號格式；in模塊將外部的信號輸入進來作為模型的輸入驅動模型進行運動，右端的pos和vel將支鏈的位移和速度計算輸出。

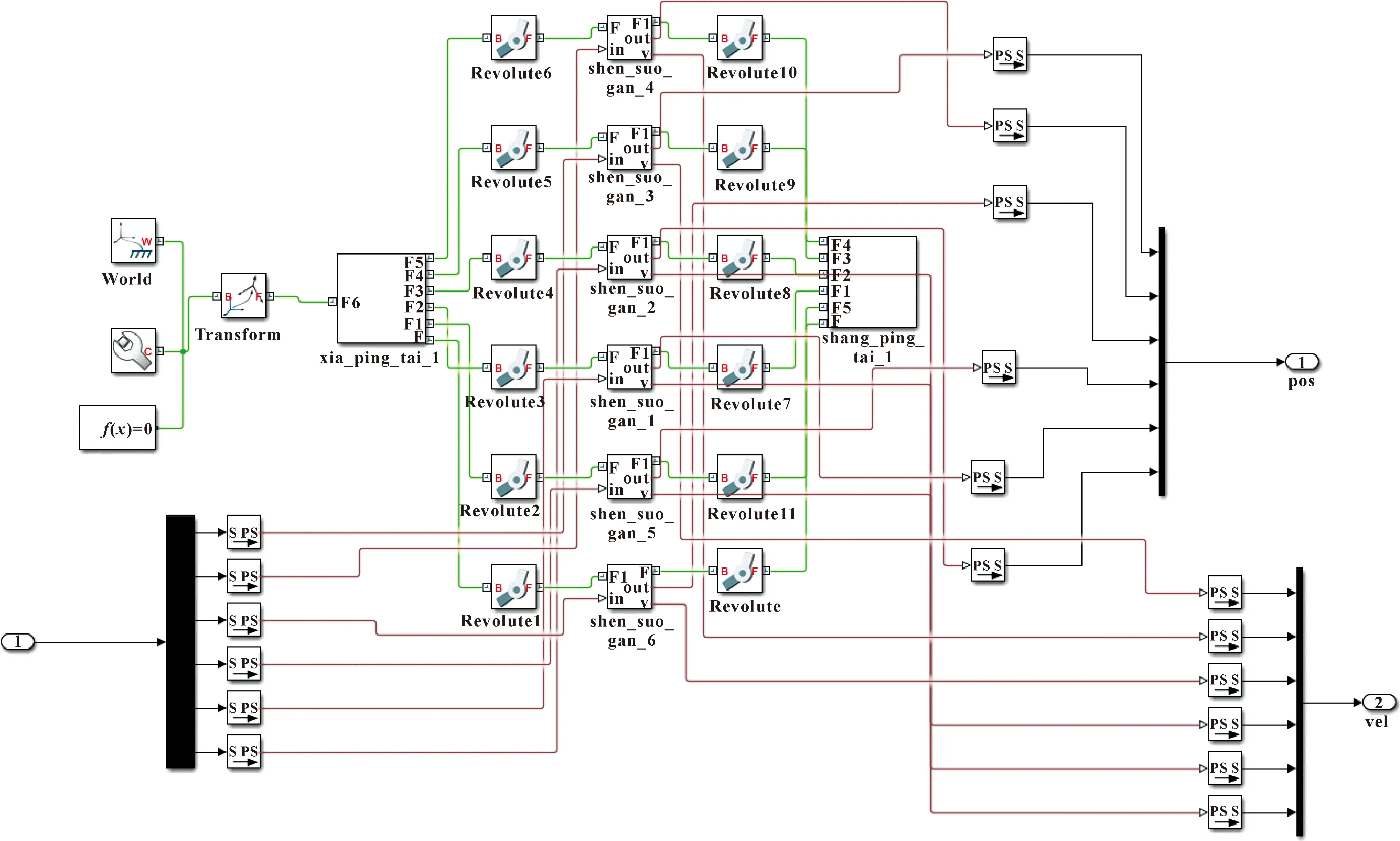
圖3 基于SimMechanics的船舶運動模擬平臺樣機模型

2 船舶運動學響應

2.1 船舶運動響應描述

船舶運動響應可看作是多個自由度的復合運動。在不同的海況下，運動響應與船舶自身航速以及相對于波浪的航向、浮體型線、質量和重心等有關。運動參數的選擇應該滿足船舶響應特性。依據5級海況下船體的運動響應程序，六自由度復合運動系統的空間姿態參數為：橫搖±30°；縱搖±7°；艏搖±5°；橫蕩±0.05 m；縱蕩±0.07 m；垂蕩±0.1 m。單自由度極限參數為：橫搖或縱搖±30°；艏搖±5°；橫蕩±0.05 m；縱蕩±0.05 m；垂蕩±0.35 m。運動周期為5 s。考慮船舶最普遍的垂蕩和縱搖耦合運動狀態，波浪周期為4 s，波幅為0.1 m，縱搖最大擺角為π/12，在MATLAB中，編寫并聯機構逆解程序，對動平臺中心輸入運動姿態表達式：

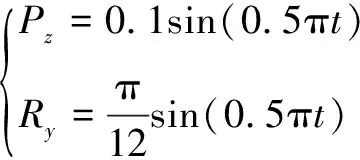
(9)

2.2 機構位姿逆解仿真結果

將動平臺期望位姿表達式輸入到上述所建立的動平臺位姿逆解計算模型中，獲得船舶模擬平臺6條支鏈伸縮位移以及伸縮速度隨時間的變化，如圖4、圖5所示。初始時刻，在動平臺自重作用下，支鏈位置略有下降。隨后，各支鏈伸縮位移和速度均呈現正弦變化規律。

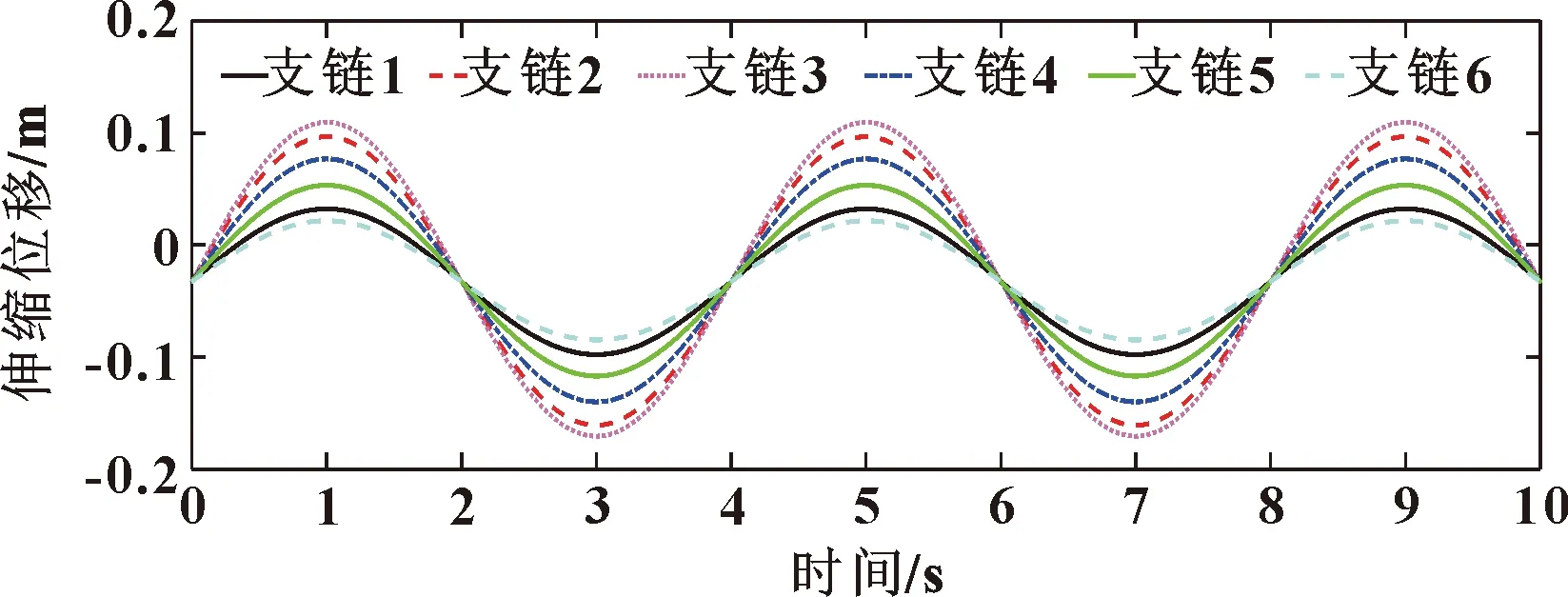
圖4 支鏈伸縮位移

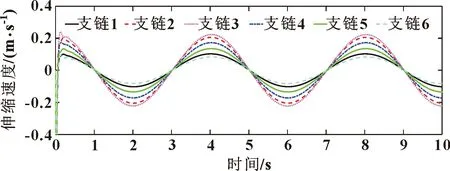
圖5 支鏈伸縮速度

圖6所示為運動模擬平臺動平臺在4個不同時刻的輸出位姿。可知：在第1、3 s時，模擬仿真動平臺呈現了較好的繞坐標軸的縱搖和垂蕩耦合運動狀態；在第2、4 s時，呈現了典型的垂蕩運動狀態。

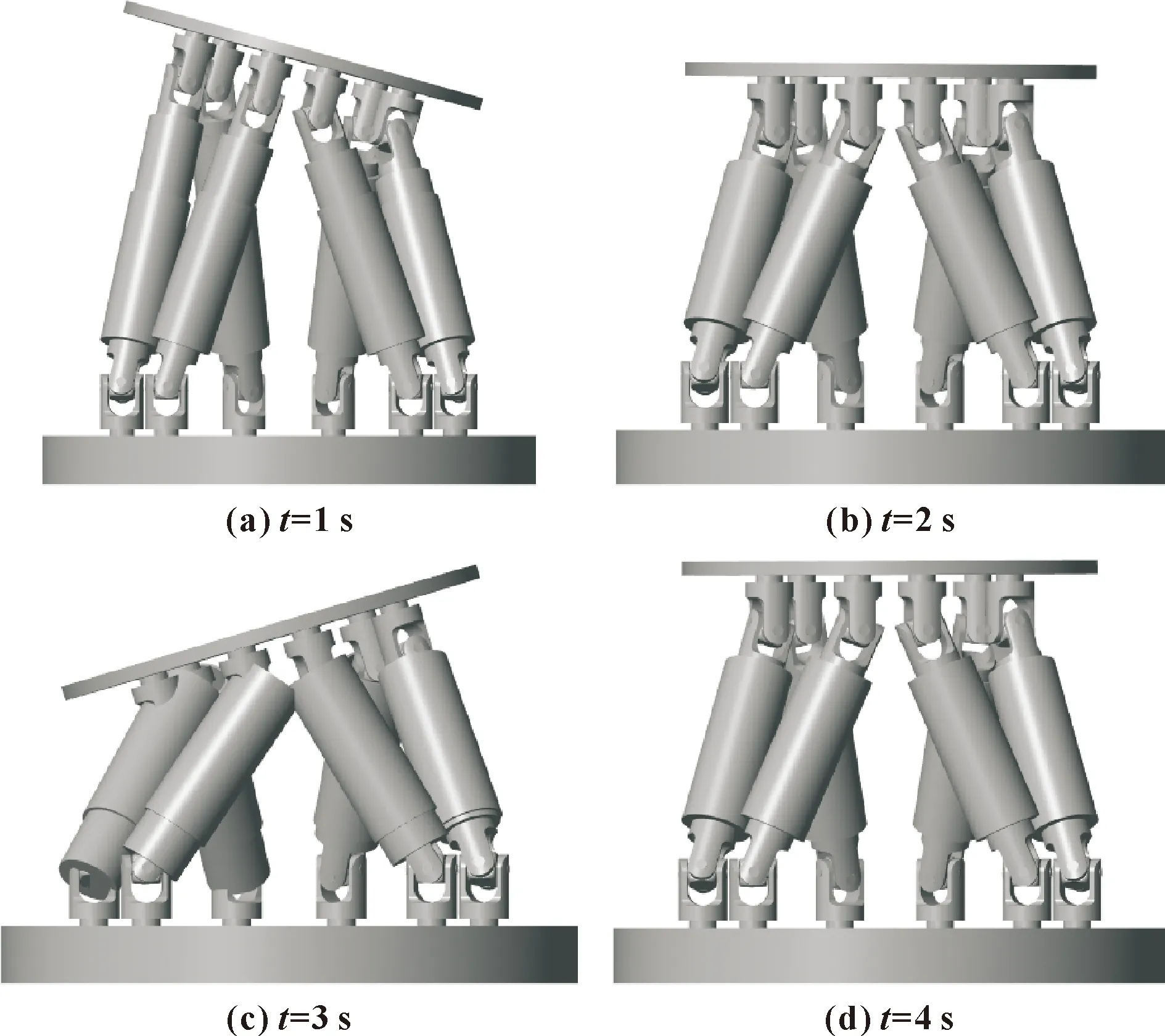
圖6 不同時刻機構位姿

3 船舶運動模擬模糊PID控制器設計與仿真

3.1 模糊PID控制原理

由于各支鏈伸縮量誤差始終在一個范圍內波動，為降低控制系統的誤差值，對PID系統的參數進行調整。模糊PID系統可以根據系統的變化自適應對PID參數進行調整，從而達到減小誤差的目的。模糊控制是一種基于規則的控制方法，利用模糊規則以及模糊條件語句來進行描述，因而不需要確定系統的精確數學模型。模糊控制器結構組成如圖7所示。

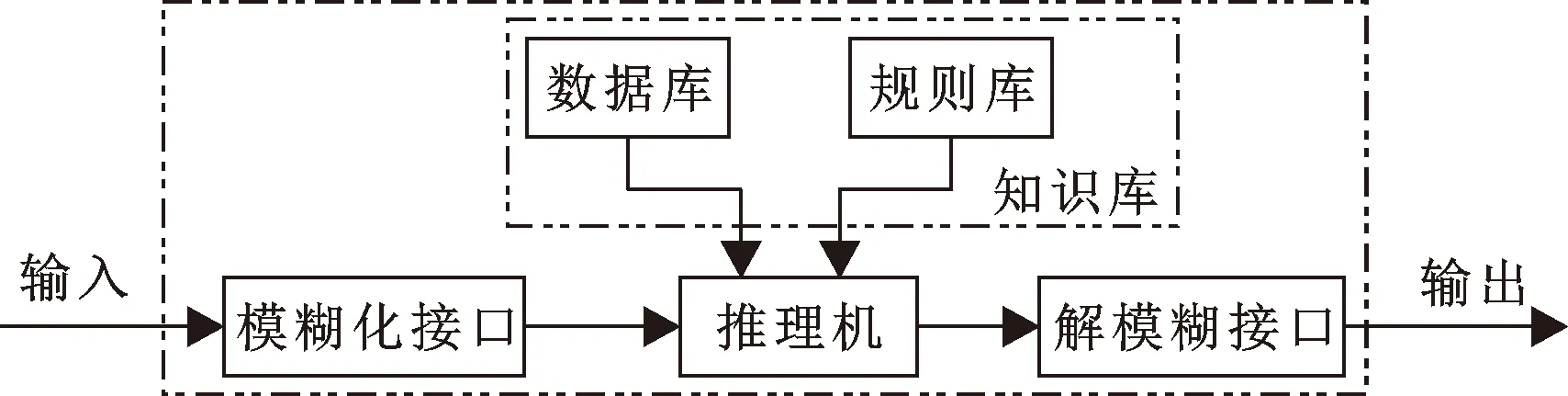
圖7 模糊控制器組成框圖

模糊PID控制器的模糊控制規則以控制誤差和誤差變化率為前提，控制規則表示為

If()=and()=

Then=(Δ,Δ,Δ)

(10)

式中：、分別為()和()的隸屬度函數；(Δ,Δ,Δ)為輸出的參數變化量，通過反模糊化求得。將式(10)輸出的參數變化量轉換成基本論域，可得PID控制器的自整定參數，有：

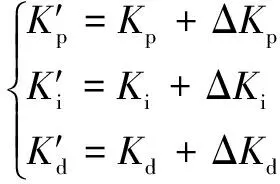
(11)

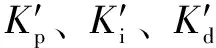
3.2 模糊PID控制系統建模

由于Stewart并聯機構模型具有旋轉對稱性，各支鏈采用相同的驅動方式和控制方式，在不考慮耦合的前提下，各支鏈自身是一個獨立的閉環控制系統。所建立的船舶模擬仿真平臺模糊PID控制系統如圖8所示。

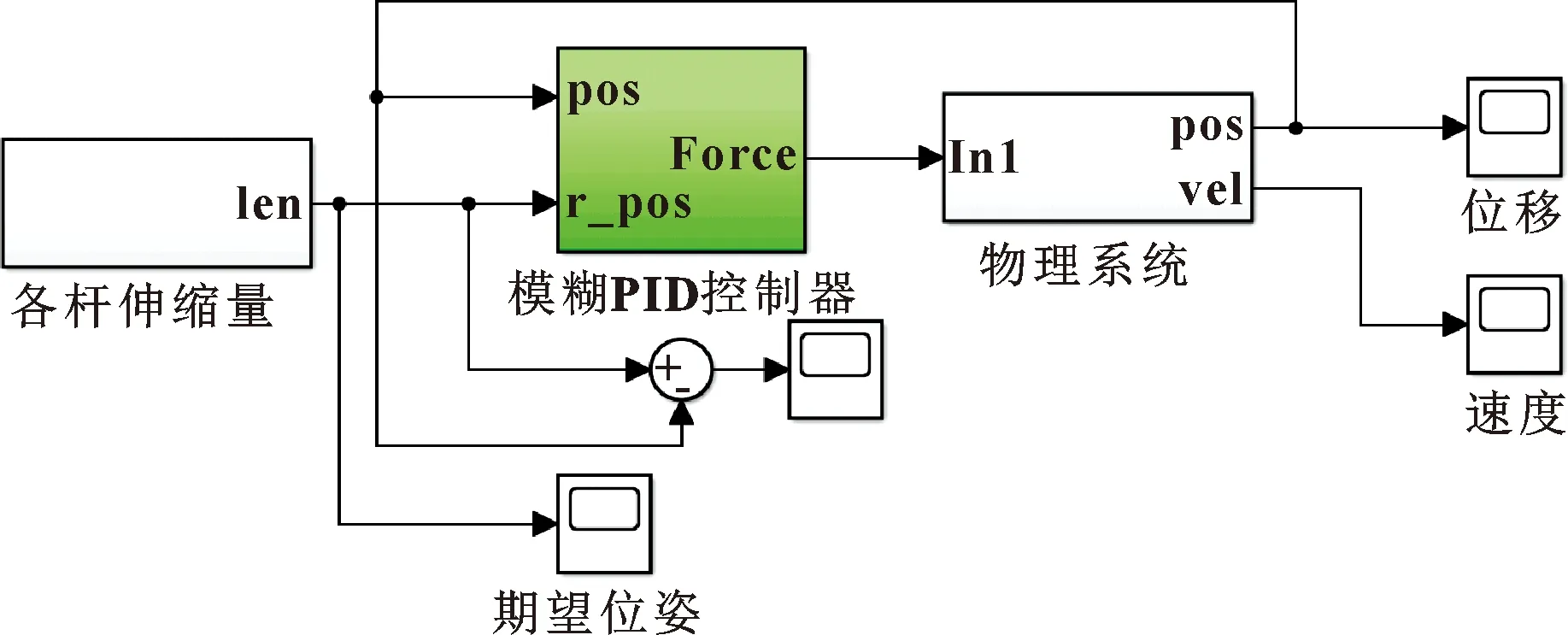
圖8 船舶運動模擬平臺仿真模型

3.3 模糊規則和隸屬度函數的確定

將=75 000、=35 000、=1 500作為模糊PID控制系統的初始值，控制系統圍繞這3個參數做自適應調整。由傳統PID控制得到各支鏈伸縮量誤差在-0.01～0.01 m之間，為使適應范圍合適，選擇其范圍為-0.03～0.03 m；模糊化模塊輸入為誤差以及誤差變化率，輸出為PID參數、和。和的模糊集為{NB, NM, NS, Z, PS, PM, PN}，和的變化范圍定義為模糊集上的論域{-0.03,0.03}。其中，NB為負數最大，NM為負數中等，NS為負數最小，Z為0值，PS為正數最小，PM為正數中間值，PB為正數最大。

根據前面的論域和模糊子集，建立、、規則，如表1—表3所示。對所有參數均采用模糊規則，則對于每一個參數都可以得到相應的模糊規則，將變量名稱和模糊規則進行一一編程。從表1—表3可以看出：當、取不同值時，、和會相應地變化，實現參數數值的自適應。

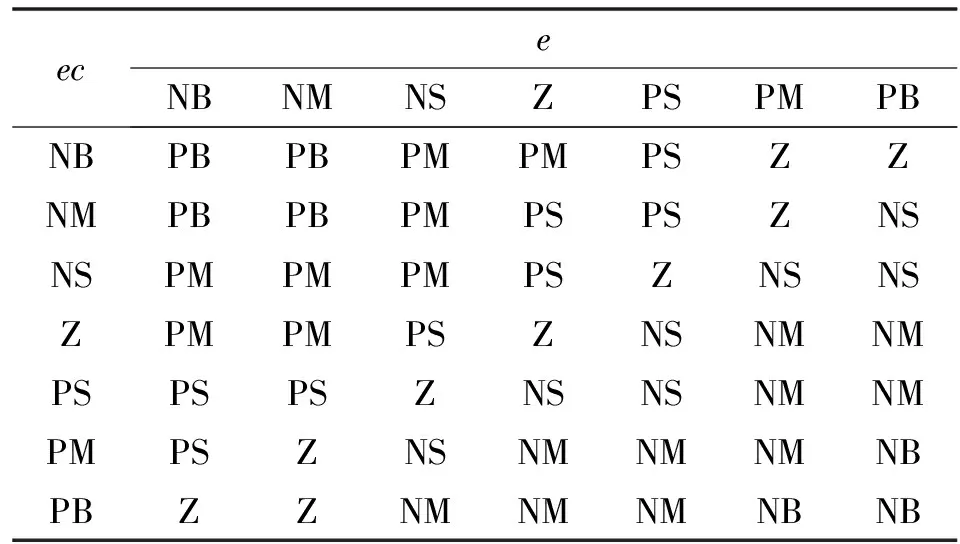
表1 Ki模糊規則

表2 Kp模糊規則

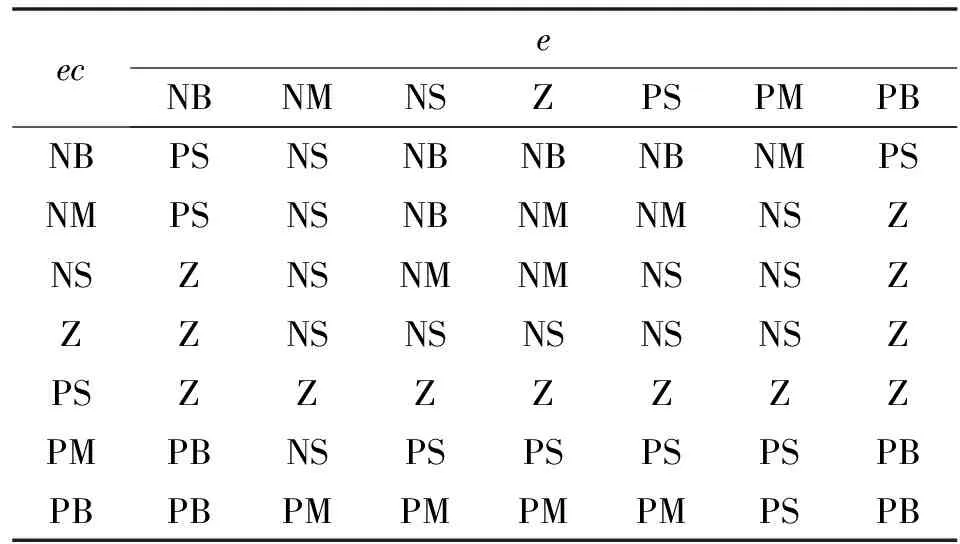
表3 Kd模糊規則

模糊化是將輸入和輸出值轉換為隸屬度函數的過程。隸屬度函數是指一個事物和某一類事物的相似程度。隸屬度函數主觀性較強，可以通過實驗得出。模糊化的結果體現了不同模糊變量中不同值的隸屬度。去模糊化是為了把得到的模糊解清晰化處理。文中將最大隸屬度函數輸出最大隸屬度值作為去模糊化方法，確定輸出參數。

系統分別采用經典PID系統與模糊PID控制算法。其中，參數設置為=75 000，=35 000，=1 500。兩個對照組的控制對象均設置如式(12)標準二階系統傳遞函數：

(12)

傳統PID與模糊PID控制誤差頻率響應對比如圖9所示。傳統PID系統超調量大，進入穩定的時間長，響應曲線不斷地穿越穩定值，達到穩定時間長，從而使誤差變大；模糊PID系統響應超調量小，響應曲線以逐漸逼近穩定值的形式達到穩定狀態，減少了振蕩誤差，從而使系統總體誤差較小。

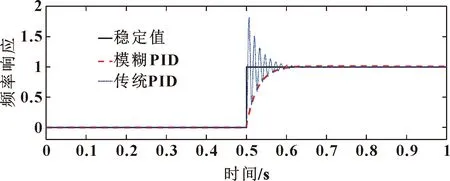
圖9 傳統PID與模糊PID控制誤差頻率響應對比

圖10所示為基于模糊PID控制算法所求解的模擬控制平臺支鏈伸縮位移。圖11所示為通過實時控制模塊，聯合SimMechanics仿真平臺獲得的物理樣機所需的支鏈驅動力。圖12、圖13所示分別為采用經典PID控制算法和采用模糊PID控制算法驅動支鏈伸縮位移與所期望達到的理論位姿的誤差曲線。結果表明：采用經典PID控制算法，初始時刻最大誤差為0.008 m，系統穩定后的最大誤差為0.005 m;而采用模糊PID控制方法，驅動支鏈在起始時刻誤差最大，最大誤差為0.003 m，之后在第2 s時誤差達到穩定狀態，誤差峰值低于0.001 m，實時快速地提升了船舶模擬平臺運動控制精度。

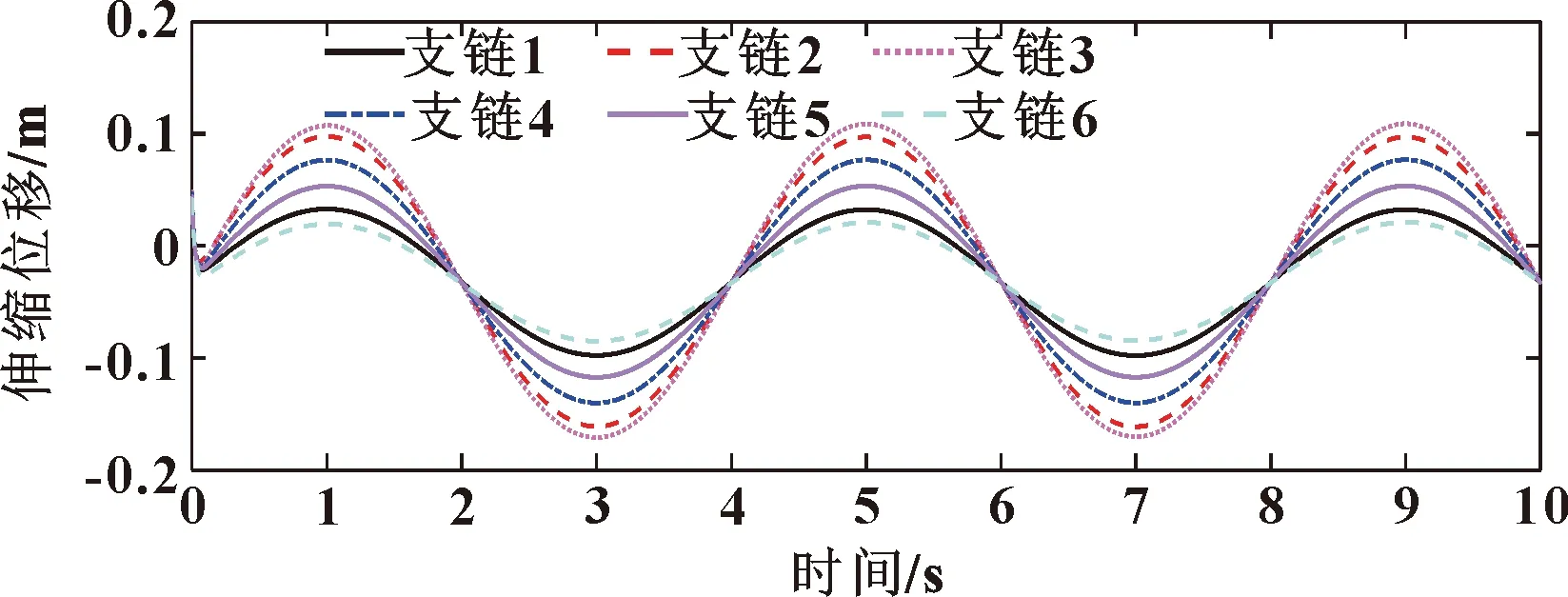
圖10 模糊PID控制輸出的位姿曲線

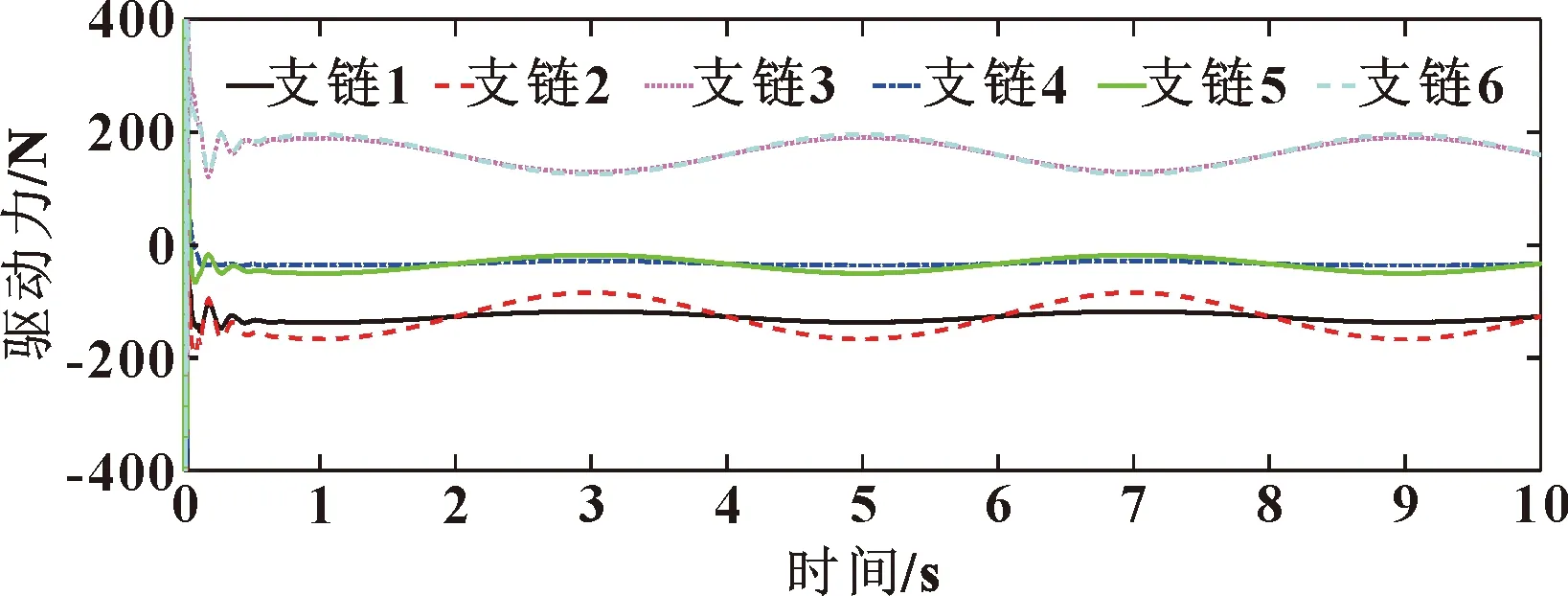
圖11 模糊PID控制輸出支鏈驅動力

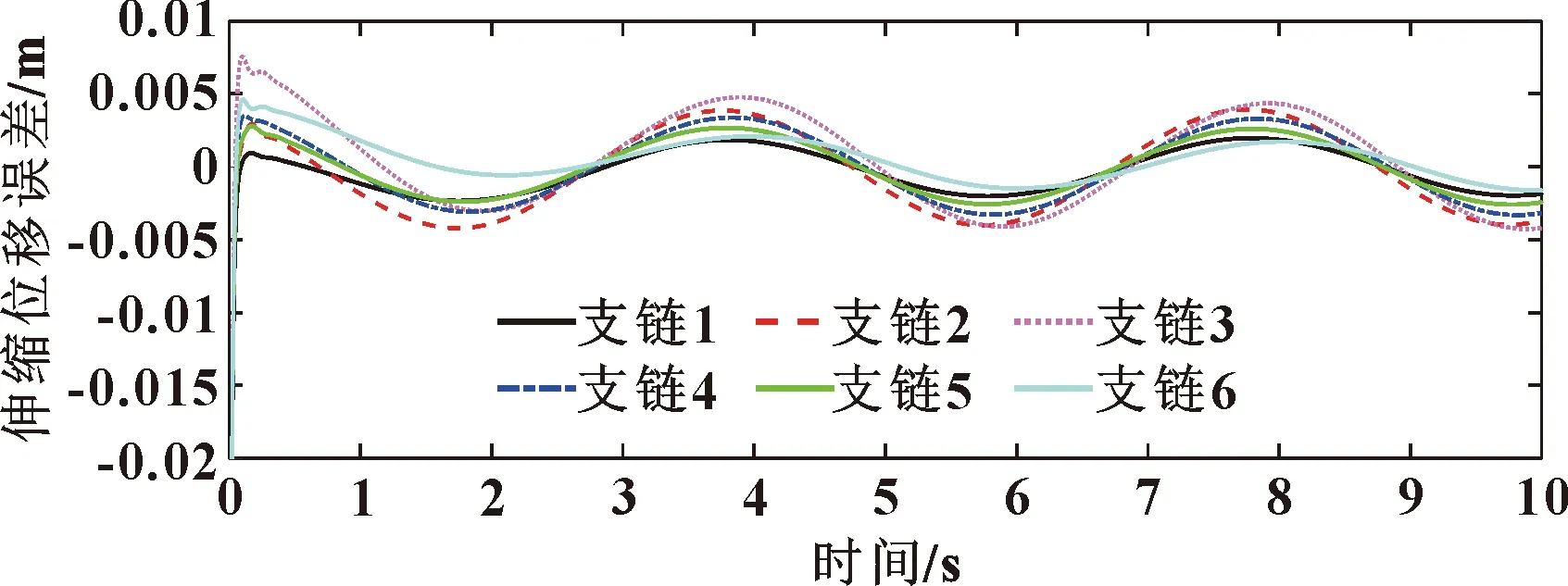
圖12 驅動支鏈伸縮位移經典PID誤差分析

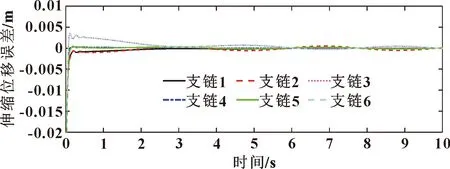
圖13 驅動支鏈伸縮位移模糊PID誤差分析

4 結論

本文作者基于Stewart并聯機構設計了六自由度船舶運動模擬仿真平臺。基于MATLAB/Simulation建立了動平臺位姿逆解模型。基于SimMechanics建立了機構虛擬樣機模型，并求解獲得樣機支鏈輸出位移。推導支鏈驅動力過程中，引入了模糊PID控制器，根據輸入的偏差和偏差變化率實時調節控制參數，實現PID參數的在線整定。結果表明：相比于傳統PID控制算法，模糊PID控制算法能夠減少系統超調量，有效提升船舶運動模擬平臺的控制精確度。