深入本質 立足建模 提升思維
——“用一元一次方程解決利潤問題”的教學與思考

付小飛

(江蘇省蘇州市第十六中學校 215003)

《義務教育數學課程標準(2022年版)》在核心素養的主要表現及其內涵中明確指出：“初步感知數學建模的基本過程，從現實生活或具體情境中抽象出數學問題，用數學符號建立方程、不等式、函數等表示數學問題中的數量關系和變化規律”．方程的本質是描述現實世界中的等量關系，更形象地說，用等號連接兩種不同的表示方法表達相同或相等的量，用方程解決問題在初中階段對培養學生數學建模能力起著至關重要的作用．但是在實際的教學過程中，有些教師習慣于將方程的應用根據題目的實際背景分成不同類型，先分析類型特征、歸納常用等量關系，再通過例題示范、變式訓練來教學．新課的教學不知不覺就變成了習題課，大量的變式題排山倒海而來，這種教學方式不僅沒有抓住方程的本質，還會多出大量的所謂解題的“套路”，一旦遇到“非標準”的類型時，學生就會束手無策，長此以往不利于學生思維水平的提升．帶著這些問題，筆者對蘇科版七年級上冊“用一元一次方程解決利潤問題”作了全新的教學設計，并在全市上了一節示范課，得到了與會專家和教師的高度評價．現對其主要的教學環節進行介紹，并且給出各環節的教學分析以及教學建議，以供同行參考．

1 創設情境，引入新知

活動1 在剛剛過去的“雙11”購物節中，小明以每個20元的價格進了一批玩具，貼上每個30元的標簽，為了吸引顧客，打出“大酬賓，九折優惠”的廣告，則進價是

元，標價是

元，售價是

元，利潤是

元，利潤率是

．

問題1：你能列舉打折促銷中的哪些常用量?

問題2：說出商家從進貨到銷售的過程中涉及哪些量?你能寫出各個量之間的關系嗎？

問題3：售價有幾種表示方式呢?

教學分析與建議

在課前可以讓學生做一次社會調查，體會商品銷售問題中的現實情境，收集各種打折銷售的活動方式．有了真實的體驗，可進一步幫助學生更深刻地理解相關術語．然后再通過問題情境，通過具體的數字，利用銷售流程(圖1)和柱狀圖(圖2)理清銷售問題各個量之間的關系，并且歸納出售價的兩種不同表示方法．這種設計從學生已有的知識經驗出發，通過創設實際的生活情境，將學生所學的數學知識與生活實際相聯系，從而激發學生的求知欲望．

圖1 圖2

2 數形探究，分析問題

活動2 商店將進價為140元的商品按標價的8折銷售，仍可獲利28元，問商品的標價為多少元？

師：如果設標價為

x

元，有幾種列式的方法？生1：0

.

8

x

=140+28．

師：請解釋一下方程兩邊所表示的意義．

生1：左邊的式子表示售價，右邊的式子也表示售價．

師：有沒有列方程的其他方法？

生2：0

.

8

x

-28=140，左邊的式子表示進價，右邊的式子也表示進價．生3：0

.

8

x

-140=28，左邊的式子表示利潤，右邊的式子也表示利潤．生4：我用的是小學學的算式的方法，(140+28)÷0

.

8．師：如果左邊用

x

表示，則可以得到

x

=(140+28)÷0

.

8，實際上這也是一個方程．

生4：左邊表示的是標價，右邊也是標價．

師：上面列出幾種不同的方程，方程的兩邊都是表示同一個量，因此我們在列方程解應用題時，可以利用題目中某些量的兩種不同表示方法來列方程．

圖3

學生討論過程中教師巡視，借助銷售條形圖(圖3)引導學生列出不同的方程．

教學分析與建議

在初中階段用方程解決實際問題時學生“最大的痛點”就是無法將實際問題中各個量用代數語言描述并構建方程．如果教師僅僅告訴學生要通過審題，找出等量關系，再列出方程，那么對于學生來說是比較含糊的，容易使學生望而生畏．因此在教學時教師要給學生指出一個明確的方向，告訴學生列方程實質上就是用兩種方式表示相同或相等的量．例如活動2中，可從以下幾個方向思考：思考1 以兩種方式表達進價，即0

.

8

x

-28=140 ①；思考2 以兩種方式表達利潤，即0

.

8

x

-140=28 ②；

思考3 以兩種方式表達8折，即③；

思考4 以兩種方式表示售價，即0

.

8

x

=140+28 ④；思考5 以兩種方式表示標價，即

x

=(140+28)÷0

.

8 ⑤

.

通過以上幾個方程的列出過程，我們可以發現題目中給出的任何一個量都可以用兩種不同方式來表示，要得到方程就是“信手拈來”，這樣為學生用方程解決實際問題指明了方向．同時利用圖表的示意作用讓思維可視化，解除了學生的畏難心理．

尤其對于方程⑤，如果把右端的

x

抹去，就是小學時的算術解法．而當學生提出用算術的方法時，如果教師直接告訴學生算術解法不如列方程來得簡潔，這時學生就會產生疑惑．初一的學生正面臨從算術思維向代數思維過渡，我們可以通過比較算術方法和方程方法的優劣性，讓學生體會從算術到方程的通性，學生自然就可以從小學的算術思想過渡到方程思想．

3 典例示范，內化新知

活動3 一件夾克衫先按成本提高50%標價，再以8折出售，結果獲利28元，這件夾克衫的成本價是多少元?

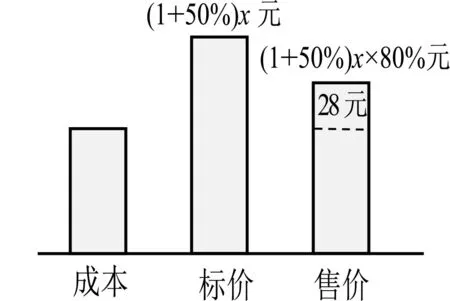
圖4

師：銷售這件夾克衫涉及哪些價格？

生1：成本、標價、售價．

師：說得很好！如果設這件夾克衫的成本是

x

元，我們可以從中找出的等量關系是什么？(生討論發言)

師：在實際操作中，我們可以畫線性示意圖或畫柱狀示意圖．

師：獲利28元是從哪里來的？(生討論發言)

師：從柱狀示意圖(圖4)中，可以得到的相等關系是什么?

生：發現售價有兩種不同的表示方法，這兩個代數式相等，即為等量關系．

(學生做，教師用多媒體演示)

師：請大家做完后想一想，還有沒有其它的量可以用不同方法表示，從而得到方程？如果有，哪一個列式方法相對簡單?

教學分析與建議

本活動的重點是借助柱狀示意圖尋找各個量之間的數量關系，嘗試多種方法列方程后，引導學生合理選擇要表達的量作為列方程的依據，突破“找等量關系”這個難點．在實際教學中，在給學生充分時間思考后，學生給出了多達8種不同的列方程的方法，通過分析比較，讓學生理解為什么在這個問題中以售價作為要表達的量最為簡捷．這就好比A要從甲地(題中的已知)送物品給乙城的B(題中設為

x

的未知量)，最為節省時間的方法就是A，B約定同時到兩地之間某個地點來交換物品．而售價就好比A，B兩人相約的地點．相當于列方程時我們思考的工作量被分成了兩段，就是分別用進價和標價來表示售價，然后用等號連接就得到方程．而小學算術解法中的算式，就相當于是A到乙城直接送交到B手中，思維上要求就更高一點．所以快速準確地找到最合適的表達量來列方程，可大大減少思考的難度．

4 自主學習，類比理解

活動4 請以下列方程各編寫一道關于商品利潤的應用題：(1)140(1+

x

)=210×80%，(2)140+28=210

x

．(學生合作交流)

生：商店將進價為140元的商品標價為210元，打八折銷售后，利潤率是多少？

生：商店將進價為140元的商品標價為210元，問商品打幾折銷售后可獲得28元的利潤？

師：你能說出方程兩邊表示的實際意義嗎？

生：方程(1)和(2)左右兩邊都是表示售價，左邊是用進價表示，右邊是用標價表示．

教學分析與建議

通過分小組討論，自編題目，互評互檢，并引導學生說出方程兩邊分別表達的量的意義，強化用兩種方式表達同一個量來列方程的解題思路．讓學生從多個方向、多個層次進行思考，

從而提升思維水平．同時，讓學生自己設計習題，也能更好地鍛煉學生的建模能力，當學生面對自己“創造”出的習題更感興趣時，練習也就更投入了．

5 合作探究，提高技能

活動5 某件商品因換季準備打折出售，如果按標價的七五折出售將賠25元；而按標價的九折出售將賺20元，問這件商品的標價是多少？

圖5

師生活動：讓學生獨立思考后，通過以下問題串，引導學生選擇用合適的量作為目標來建立相等關系列方程：

(1)題目中涉及到幾種價格？

(2)你能否準確設出未知數?

(3)你能否畫出本題中的柱狀示意圖?

(4)你能否用不同的方式來表達這個量?

(5)你認為選哪一個量作為列方程的依據最為簡單?

教學分析與建議

通過活動5，讓學生進一步學習如何合理選擇要表達的量．在教學時可類比盈不足問題選取不變的量．比如：“某工廠計劃做一批“中國結”，如果每人做5個，那么比計劃多做了9個；如果每人做4個，那么比計劃少做了15個，問：該小組共有多少名成員?他們計劃做多少個中國結?”我們可以選擇原計劃制作的中國結總數的兩種不同表示來列方程，如果設小組成員有

x

名，則可列方程：5

x

-9=4

x

+15．也可以選擇小組總成員數的兩種不同表示來列方程，設計劃做

x

個中國結，可列方程：通過這樣的類比練習，進一步培養學生的建模能力，提升思維水平．

列方程解決實際問題的學習對學生以后學習分式方程、不等式以及函數都有一定的啟發作用，所以學生學習本章的結果將直接影響學生對后續內容的理解與掌握．《義務教學數學課程標準(2022年版)》要求“應當讓學生經歷對現實問題中量的分析，借助用字母表達的未知數，建立兩個量之間關系的過程，知道方程或不等式是現實問題中含有未知數的等量關系或不等關系的數學表達；體會算術與代數的差異．”基于這些原因，在教學設計的過程中，務必力求做到從學生已有知識經驗出發，注重新舊知識的聯系，恰當地使用信息技術，做到一題多解，重視展示思維過程，讓學生通過比較來感悟方程解決問題的優越性，從中了解和體會數學地研究問題的思路與方法．