極限思想在高中數學中的運用
——以圓錐曲線為例

姚 婷 吳如光

(南京師范大學附屬中學秦淮科技高中 210003)

1 背景分析

極限對于學生來說并不陌生，小學階段對于無窮大的數的感悟，初中階段對于反比例函數圖象的探究，高中階段對于加速度概念的理解，無一不滲透著極限思想．章建躍博士在文[1]中指出：“在中學階段,掌握一些微積分的初步知識,對發展學生的理性思維、增強數學應用能力等都是非常有用的．”極限思想是一種重要的數學思想，雖然高中數學教材中沒有明確極限的概念，但極限思想卻始終貫穿著高中數學的學習，以導數為典型，解析幾何、立體幾何、數列、三角函數等內容的學習過程中也繞不開極限．雖然高等數學中用“

ε

-

δ

”語言表述的極限定義對于中學生來講難以接受，但是極限思想卻是可以在學習中不斷滲透的．利用極限思想，往往可以引導解題方向、規避復雜運算、突破解題難點．本文將結合圓錐曲線談談極限思想在高中數學中的運用．

2 引例分析

近日，筆者在教學中遇到這樣一道解析幾何綜合題：已知點是橢圓上一點，

F

，

F

分別是橢圓的左、右焦點，

PF

+

PF

=4．設直線

l

不經過點

P

且與橢圓

C

相交于

A

，

B

兩點．若直線

PA

與直線

PB

的斜率之和為1，問直線

l

是否過定點？證明你的結論．易得橢圓方程為可設直線

l

的方程

y

=

kx

+

m

，

A

(

x

，

y

)，

B

(

x

，

y

)，運用方程思想將直線方程與橢圓方程聯立，通過韋達定理得

x

+

x

再由直線

PA

與直線

PB

的斜率之和為1得整理得化簡得2

m

-3

m

+8

k

+12

k

-10

km

=0，因式分解得(

m

-4

k

)(2

m

-2

k

-3)=0，從而確定直線

l

：

y

=

k

(

x

+4)過定點(-4，0)．在高三一輪復習過程中，筆者發現，學生能熟練運用方程思想聯立方程組，并通過韋達定理得

A

，

B

兩點坐標之間的關系，解題的難點在于，轉化條件

k

+

k

=1后得到的關于

k

，

m

的二次式該如何處置？有經驗的學生知道要因式分解，但不知如何分解

.

如果能順利分解因式，問題就迎刃而解．教學中教師如果僅僅告知學生，這一步需要因式分解，即便教會學生“雙十字相乘”因式分解法，學生對于相似的題型仍然是茫然的．解題教學不應當局限于這一道題的解法，更應引導學生厘清問題的本質．筆者認為，有幾個問題是必須要搞清楚的： ①為什么直線

l

過定點？②為什么需要因式分解？③因式分解后得到的因式之一恰好過點

P

，這是偶然還是必然？④最后求得的定點在

x

軸上，這又是偶然還是必然？首先關于問題①②，直線

l

的方程為

y

=

kx

+

m

，由于

k

+

k

=1，直線

l

中的參數

k

，

m

必然有著確定的關系，故直線

l

有可能過定點或定斜率；反之，若直線

l

過定點，則必存在

k

與

m

的線性關系，故得到關于

k

，

m

的二次式后需要想辦法進行因式分解．其次，要解決問題③④，就需要搞清楚直線

l

是如何變化的

.

教學中可用幾何畫板或GGB等作圖軟件來動態演示直線

l

的變化規律

.

由于

k

+

k

=1，那么

k

確定，

k

隨之確定，故只需通過運動點

A

來探究變化規律．當點

A

沿橢圓無限趨近于點

P

時，

k

就無限接近橢圓在點

P

處的切線的斜率，由橢圓上任一點(

x

，

y

)處的切線斜率為可知，

k

無限接近而此時，由于

k

+

k

=1，點

B

也在沿橢圓無限趨近于點

P

，故

k

也無限接近直線

l

在無限逼近點

P

處的切線

l

．另一方面，當直線

PA

的斜率無限增大，趨向于 +∞時，直線

PB

的斜率無限減小，趨向于-∞，此時，直線

l

無限逼近點處的切線

l

．

l

與

l

斜率顯然不等，故直線

l

不可能定斜率，可能過定點，

l

與

l

關于

x

軸對稱，則所經過的定點必在

x

軸上，即為

l

與

l

的交點(-4，0)．

3 極限思想的運用

3

.

1 尋找極限位置，確定定點

事實上，對于引例，我們可以作更深層次的思考，若改變題設條件，將“

k

+

k

=1”改為“

k

+

k

=2”，其余條件、問題不變，探究直線

l

的變化規律．不妨考慮某些特殊位置，當

k

=

k

=1時，直線

l

的極限位置是橢圓在點處的切線

l

；當直線

PA

的斜率無限增大，趨近于 +∞時，直線

PB

的斜率無限減小，趨近于-∞時，直線

l

的極限位置就是橢圓在處的切線

l

，顯然，

l

與

l

斜率不等，故直線

l

過定點即為

l

與

l

的交點．更一般地，已知

P

(

x

，

y

)為曲線上一點，設直線

l

不經過點

P

且與橢圓

C

相交于

A

，

B

兩點．若直線

PA

與直線

PB

的斜率之和為

λ

，則直線

l

過定點而且，由于證明過程是可逆的，反之也成立．順勢而為，教學時還可以引導學生探究：若

k

k

=1，直線

l

是否過定點？推廣到一般，已知

P

(

x

，

y

)為曲線上一點，設直線

l

不經過點

P

且與橢圓

C

相交于

A

，

B

兩點．若直線

PA

與直線

PB

的斜率之積為則直線

l

過定點探究動直線的變化規律，尋找極限位置，能快速確定定點位置．

3

.

2 利用極限位置，計算定值

例1

已知橢圓的離心率為橢圓

C

的下頂點和上頂點分別為

B

，

B

，且

B

B

=2,過點

P

(0，2)且斜率為

k

的直線

l

與橢圓

C

交于

M

，

N

兩點．求證：直線

B

M

與直線

B

N

的交點

T

的縱坐標為定值．

解析

易得橢圓的標準方程為+

y

=1，設

M

(

x

,

y

)，

N

(

x

,

y

)，設直線

l

的方程并和橢圓進行聯立，得設

T

(

m

，

n

)，再由

B

，

T

，

M

在同一條直線上，得在同一條直線上，得化簡得故交點

T

的縱坐標為定值點評 換個角度來思考該問題，直線

l

在變化過程中，極限位置是與橢圓相切，此時直線

B

M

與直線

B

N

交于一點，該點即為直線

l

與橢圓相切的切點，該點的縱坐標即為所求．利用極限思想，可以快速確定定值．

3

.

3 運用極限思想，求解范圍

例2

設雙曲線的左、右焦點分別為

F

，

F

．若點

P

在雙曲線上，且△

F

PF

為銳角三角形，則

PF

+

PF

的取值范圍是

．

解析

由已知得則設

P

(

x

，

y

)是雙曲線上任一點，由對稱性不妨設

P

在雙曲線的右支上，則1<

x

<2，

PF

=2

x

+1，

PF

=2

x

-1，∠

F

PF

為銳角，則即(2

x

+1)+(2

x

-1)>42，解得所以則點評 利用極限思想，不妨考慮極限位置(由于雙曲線的對稱性，可將點

P

置于第一象限來考慮)，當△

F

PF

為直角三角形時，有兩種情況：若∠

F

PF

為直角，

PF

+

PF

=2；若∠

PF

F

為直角，

PF

+

PF

=8

.

由圖形上點

P

的運動規律可知，△

F

PF

為銳角三角形時，對于填空題，利用極限思想解決范圍問題，省時省力；對于解答題，先探究動點的運動軌跡，可以幫助確定變量

.

如該題中，

PF

+

PF

的變化源于點

P

，點

P

在第一象限的變化可由橫坐標這一單一變量控制，于是只需用點

P

的橫坐標來表示目標．引導學生利用極限思想來求解范圍，從運動的觀點來解決問題，有利于發展學生的理性思維．

4 幾點教學建議

4

.

1 分析極限狀態，明辨解題思路

例3

已知直線

y

=2

x

與橢圓

E

：

x

+2

y

=1交于

A

，

B

兩點(點

A

在第一象限)，點

P

(-4

t

，

t

)在橢圓

E

內部，射線

AP

，

BP

與橢圓

E

的另一交點分別為

C

，

D

．求證：直線

CD

的斜率為定值．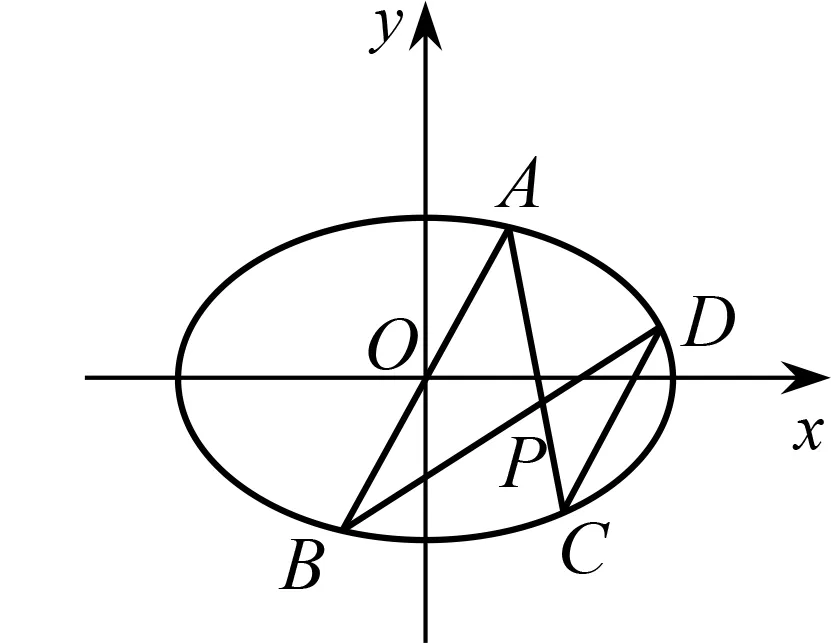

圖2

解析

對于該題，易想到的思路是求出

A

，

B

兩點，聯立直線

AP

與橢圓方程得

C

點坐標，聯立直線

BP

與橢圓方程得

D

點坐標，再求直線

CD

的斜率．但是，該思路計算量很大，求解困難．不妨利用極限思想重新審視該題，點

P

在定直線上運動，顯然直線與橢圓有兩個交點，當點

P

無限接近這其中一個交點時，直線

CD

的極限位置就是在該交點處的切線，那么直線

CD

的斜率即為該切線的斜率，易得斜率為2．還可以考慮另一個極限位置，當點

P

無限接近坐標原點時，直線

CD

的極限位置就是直線

AB

，故直線

CD

的斜率為2．預知直線

CD

的斜率為2，那么該題的證明思路就更加清晰了，即需證明

AB

∥

CD

，聯想到向量，即證

λ

=

λ

．解析幾何的解題思路非常重要，因為計算量大，往往“沒有回頭路”，教學中一定要引導學生先分析解題思路，理清楚解題步驟，預估計算量，計算時多想兩步，才能簡化計算，高效解題．利用極限思想判斷出直線

CD

的斜率為2，為后續的證明打開了思路，抓住了變化中的不變量，解題方向更加清晰．

證明

設

P

(

x

，

y

)，

A

(

x

，

y

)，

B

(

x

，

y

)，

C

(

x

，

y

)，

D

(

x

，

y

)，則又設其中

λ

，

λ

∈

R

，則代入橢圓

x

+2

y

=1并整理得從而有①

同理可得，②

結合

x

=-4

t

，

y

=

t

，

A

，

B

兩點均在直線

y

=2

x

上

.

由①-②，得因為所以

λ

=

λ

．從而

AB

∥

CD

，故

CD

的斜率為定值．

4

.

2 妙用極限思想，優化解題過程

例4

已知拋物線

C

：

y

=8

x

，在

x

軸的正半軸上，是否存在某個確定的點

M

，過該點的動直線

l

與拋物線

C

交于

A

，

B

兩點，使得為定值？如果存在，求出點

M

的坐標；如果不存在，請說明理由．

解析

假設存在滿足條件的點

M

(

m

，0)(

m

>0)，設直線

l

：

x

=

ty

+

m

，與拋物線方程聯立，有設

A

(

x

，

y

)，

B

(

x

，

y

)，有

y

+

y

=8

t

，

y

y

=-8

m.

當

m

=4時，為定值，所以

M

(4，0)．點評 假設存在點

M

滿足條件，因為過點

M

的任意一條弦為定值，那么對于垂直于

x

軸的弦

AB

也滿足．當直線

AB

垂直于

x

軸時，設

M

(

x

，0)，

A

(

x

，

y

)，

B

(

x

，-

y

)，則對于這一特殊位置，還不能確定定點和定值，不妨考慮另一個極限位置．當點

A

無限接近原點

O

時，點

B

沿

x

軸無限延伸，橫坐標趨向于趨向于趨向于令可得

x

=4，故預判出定點為(4,0)，那么后續只需證明點過的任一弦

AB

均有提前預判出定點和定值，那么解題過程中就不需要設2個參量，只需引入直線的斜率這一個參量即可，這就大大簡化了計算，優化了解題過程，這對于計算能力薄弱的學生是非常必要的．

在上述例題中，動直線的極限狀態往往是切線或過已知點狀態，若動直線過定點，則極限狀態也過定點，所以兩種極限狀態下同時滿足的定點通常可以預判，這樣也給我們后面的解答指引了目標，即便用常規方式計算也會因此由漫無目的變得有的放矢．例如雙二次的因式分解因為定點已知，從而分解更加容易．

4

.

3 活用極限思想，提升核心素養

面對新高考，我們總在強調“思維能力的培養”，這不僅是一句口號，而是需要一線教師在教學過程中不斷摸索的

.

過去，我們在課堂中常會幫助學生總結解決問題的一般方法并歸納分類，這對于應試是能起到一定作用的，但題目是千變萬化的，如何能讓學生在面對各種問題時，自我分析，自我探究，自我解決，是需要教師不斷引導的

.

雖說極限思想不能直接用來求解圓錐曲線綜合題，但是對于引導學生學會自我探究起到了積極的作用

.

上述例題中，利用極限思想來解決的過程，均是抓住了題目中的動點和動直線，尋找變化規律，這對于學生來說，是提升理性思維、抽象能力的絕佳時機

.

解題教學時，唯有多想一點，才能少算一點，多反思才能不斷優化解題過程，多總結歸納才能以不變應萬變，多復盤才能不斷提升．數學教育的本質是傳授數學思想，教學生學會思考

.

極限思想在高中數學中的運用，不僅能提升學生的解題能力，還能提升核心素養，讓學生站在更高的角度去思考、理解問題，知其然并知其所以然，更為今后高等數學的學習奠定基礎．