PZT尺寸與位置對傳感器導納的影響

張耀文，趙 晶，何 穎，霍林生

(1.大連交通大學 材料科學與工程學院,遼寧 大連116028; 2.大連科技學院 交通運輸學院,遼寧 大連 116052; 3.大連理工大學 建設工程學部,遼寧 大連 116024)

0 引言

壓電阻抗法在結構健康監測中已有廣泛應用。韓芳等[1]應用壓電阻抗法對木梁的損傷進行了識別研究。Liu等[2]應用壓電阻抗法對混凝土的損傷進行識別診斷。Tawie等[3]使用壓電阻抗法監測混凝土的強度變化。Cheng等[4]把壓電阻抗法用于螺栓松動的檢測。

壓電阻抗法通常使用鋯鈦酸鉛壓電陶瓷(PZT)片作為傳感器。當被測結構出現損傷時，粘貼于結構表面或嵌入到結構內部PZT片的導納會發生變化，對比損傷前后PZT的導納曲線，即可識別出損傷。壓電阻抗法的有效性依賴于對檢測頻率、PZT尺寸、膠層影響、敏感范圍、基體材料與尺寸及環境溫度等因素的合理選擇和把握[5]。Baptista等[6]研究了PZT尺寸對壓電阻抗法敏感度的影響，以機械阻抗概念的理論為基礎研究得出，1塊200 mm×500 mm×2 mm的鋁板需要1個72.4 mm×72.4 mm×0.264 mm的PZT片才能滿足檢測的靈敏度要求，與實際應用不符。Hire等[7]以Giurgiutiu等[8]的理論模型為依據，使用動剛度比(假定與頻率無關)分析了PZT尺寸與壓電阻抗法敏感度的關系，得出小尺寸PZT片的傳感范圍相對較大的結論，與實際應用也不符。Naidu等[9]通過有限元分析研究了PZT片粘貼在一個細小金屬懸臂梁上不同位置時其導納曲線的變化，結果發現，粘貼位置對導納曲線影響很大，但并未開展相應的實驗研究，且未研究結果是否適用于尺寸相對較大的結構。在這些研究中，關于PZT尺寸及粘貼位置對PZT導納特性的影響機理尚不明確。因此，難以形成可以用于指導實際應用的原則或方法。

本文首先分析了粘貼條件下PZT圓片導納模型和測量原理，然后通過設計對比實驗，對其影響機理進行了研究，為PZT尺寸的選擇及粘貼位置的確定提供了參考依據。

1 PZT圓片粘貼條件的導納模型與測量

圖1為PZT圓片粘貼與約束示意圖。圖中PZT圓片因直徑遠大于厚度，當施加的電壓信號頻率較低時，主要沿徑向振動。粘貼前，徑向無約束條件，振動為自由振動。當把PZT粘貼到被測結構表面或嵌入被測結構內部時，其力學邊界條件發生了變化，并導致諧振頻率也會發生變化。因此，粘貼或嵌入被測結構后，PZT傳感器的導納曲線會因約束而發生改變。

如圖1所示，將圓形PZT薄片粘貼到結構表面，若把粘貼帶來的約束簡化為結構的動剛度kstr(ω)[10]，即:

Na=-kstr(ω)ua

(1)

式中：a為PZT片的半徑；Na為PZT圓片在r=a處的邊界力；ω為圓頻率；ua為r=a處PZT圓片的位移。

PZT片徑向振動的電導納為

(2)

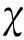
(3)

(4)

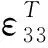
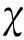
PZT的導納通常使用阻抗分析儀來測量。首先設定測量的起止頻率和檢測點數，隨后阻抗分析儀會對PZT依次施加各個頻率的單頻正弦交變電壓信號。阻抗分析儀基于自動平衡電橋測量導納，針對每個待測量的頻率，施加多周期的電壓信號，從檢測電壓信號中提取一段較穩定的信號計算導納。因此，在測量導納時，PZT持續激發出超聲波(聲波)，若超聲波遇到結構邊界或損傷后反射回到PZT的粘貼位置，且依然有足夠強的能量時，將影響PZT的力學邊界條件，進而影響PZT的振動情況，導致測量的導納值發生變化。不同頻率的超聲波因波長不同，在結構中的傳播路徑及對PZT的力學邊界條件也不同，故用動剛度來表達粘貼帶來的約束時，需用頻率的函數來表示。

通過以上分析可知，動剛度雖然只表示PZT圓片周向的邊界約束，但因導納測量過程中結構中存在超聲波，動剛度的值會隨頻率而變化。因此，壓電阻抗法能識別結構損傷等變化的前提是變化能對動剛度產生有效影響，這依賴于兩個條件：

1) 結構變化會對超聲波傳播產生有效影響，如改變傳播路徑，造成能量衰減等。

2) 受影響的超聲波返回到PZT粘貼位置時，能量足夠大，對PZT的邊界產生有效影響。

當同時存在損傷及溫度變化等多種結構變化因素時，壓電阻抗法的有效性還依賴于各因素對動剛度的影響不互相抵消，這種抵消現象在Campos等[11]的研究中已有發現。

滿足上述兩個條件，對PZT尺寸及粘貼位置還有要求。尺寸過小，激發的超聲波能量在被測結構中傳播后，就不足以對PZT的邊界產生有效影響。尺寸過大，不僅造成浪費，還會有經濟性差及易損壞等問題，而粘貼位置涉及檢測范圍等問題。因此，掌握了尺寸與粘貼位置對PZT導納的影響規律，能有效地指導壓電阻抗法的應用。以下通過對比實驗來研究PZT的尺寸和粘貼位置對其導納曲線的影響規律。

2 實驗設計

實驗選擇了相同厚度(1 mm)、不同直徑(?10 mm、?16 mm、?25 mm)的3種PZT-5H圓片，每種2片，分別標為C10、E10、C16、E16、C25、E25。測量導納的設備為E4990A阻抗分析儀，測量頻段為1 kHz～1 MHz。因該阻抗分析儀每次測量的頻率點數最多為1 601，為獲得更多頻率點的導納值，把整個測量頻段分為10段，1～100 kHz，100～200 kHz，200～300 kHz，…，900 kHz～1 MHz。每段的檢測頻率點數設置為1 600。其中，1～100 kHz頻段采用對數掃描，其他頻段采用線性掃描。

為盡可能地符合圓片徑向自由振動的邊界條件，采用自制的測量夾具(見圖2)，僅夾持PZT圓片的圓心進行測量6個PZT圓片的自由狀態導納。圖2中夾具的基體經3D打印制作，探針使用商用的探針改造而成。

圖2 PZT圓片自由狀態導納測量夾具

把6個PZT圓片(C10、E10、C16、E16、C25、E25)分兩組粘貼在直徑?470 mm、厚5 mm的圓形鋼板上，如圖3所示。用超聲波振動專用膠水(科美達KMD-398)粘貼后，使用1 kg的鋼塊進行按壓固化24 h，盡量減少粘膠差別對實驗的影響。待固化后，給每個PZT片焊接導線后依次進行導納測量。測量過程中，鋼板使用泡沫板支撐。

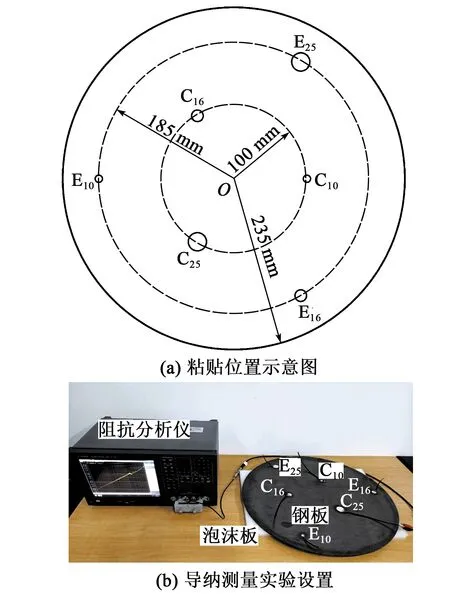
圖3 PZT片的粘貼位置與導納測量實驗設置示意圖

3 實驗結果與分析

3.1 自由狀態與粘貼狀態導納對比

不同直徑PZT圓片的自由狀態導納曲線和粘貼后的導納曲線如圖4所示。圖中各個子圖曲線為導納曲線局部放大圖，突出顯示了各階諧振頻率所在的頻段；各子圖中小窗口內的曲線為整個檢測頻段的導納曲線。由圖4可看出，與自由狀態相比，PZT片粘貼后，導納曲線變化較大，諧振頻率增大(右移)，諧振處導納幅值減小，導納曲線布滿局部密集峰。諧振頻率的偏移表明動剛度會改變PZT的諧振頻率。局部密集峰的出現表明動剛度隨頻率而變化。結合第2節中的分析，動剛度的改變意味著結構信息在導納曲線上的有效體現。因此，與平滑頻段相比，局部密集峰中包含有更多的結構信息。由圖4還可發現，強度較大的密集峰主要分布于諧振頻段。

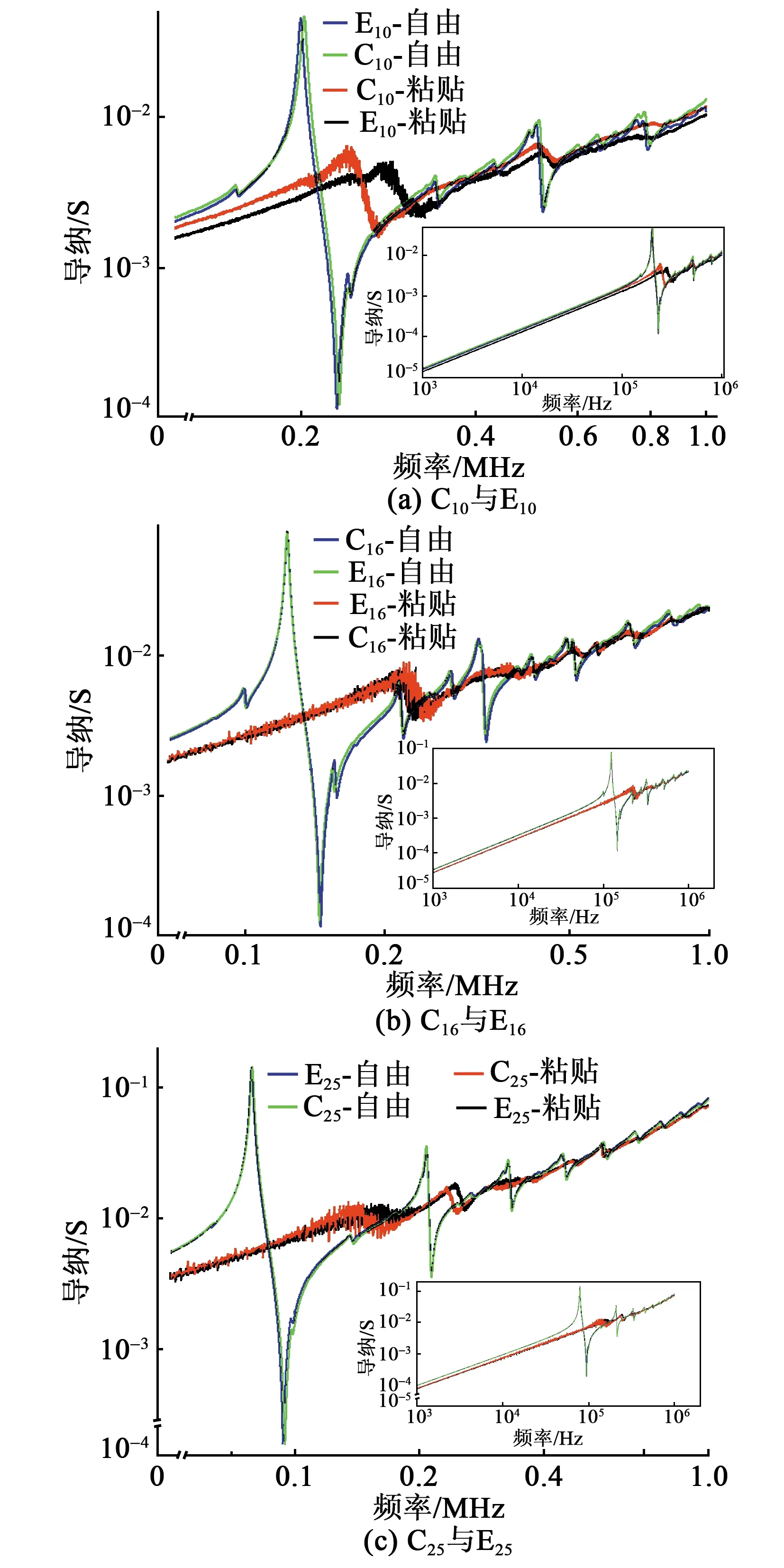
圖4 不同直徑圓片粘貼前后導納測量結果

3.2 局部峰提取與分析

為了對比局部密集峰，采用非對稱最小二乘平滑算法對粘貼后的PZT導納曲線創建基線，進而把導納的主體部分和局部密集峰進行分離。創建基線時參數設置如表1所示。基線創建及局部密集峰分離的結果如圖5所示。

表1 非對稱最小二乘平滑模式創建基線的參數設置

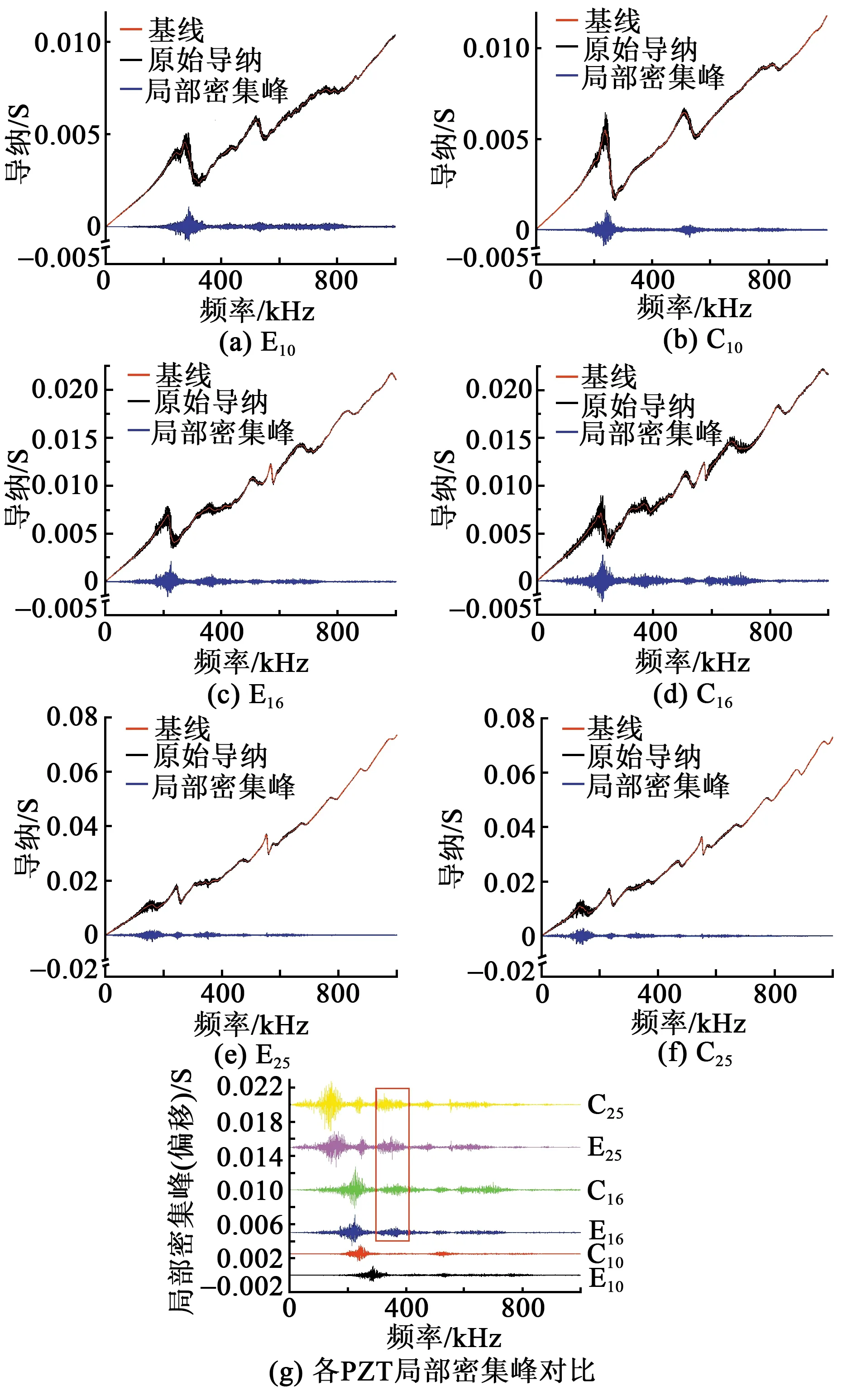
圖5 導納曲線基線創建及局部密集峰分離結果對比

3種不同直徑的PZT片的導納曲線差別較大，由圖5(a)～(f)可知各導納值不同。由圖5 (g)可知，局部密集峰的數據是分別做了不同的整體偏移所得，從下到上導納偏移量依次為0、0.002 5 S、0.005 S、0.01 S、0.015 S、0.02 S。

由圖5可看出，在每個PZT片的諧振頻段局部密集峰的強度較大，其他頻段相對較小；對于同一個PZT片，局部密集峰強度在基頻諧振頻段處最大，二、三階諧振頻率依次減小，在更高階的諧振頻段很弱。對比圖5(g)不同直徑PZT片的前兩階諧振頻段可發現，直徑越大，局部密集峰的強度也越大。由圖5(g)中紅色矩形框所示頻段可知，直徑?25 mm、?16 mm的PZT的導納都有較強的局部密集峰，但直徑?25 mm的PZT片局部密集峰強度較大。

綜上所述可知，對于相同結構的PZT，PZT片尺寸越大，其諧振頻段的局部密集峰越強，攜帶有結構有效信息的頻段也越多。應用壓電阻抗法時，結合損傷尺寸等因素確定檢測頻段后，應根據PZT粘貼后各階諧振頻率段的局部密集峰來決定PZT尺寸。結合圖5(g)，如果檢測頻段為100～200 kHz，則直徑?25 mm的PZT片更適合。若檢測頻段為200～300 kHz，雖然3種尺寸的PZT片都有較強的局部密集峰，但考慮到經濟性等因素，直徑?10mm的PZT片更適合。

由于粘貼后諧振頻率偏移，所以檢測頻段的選擇不能直接根據自由狀態的諧振頻段來確定[12]。而關于諧振頻率的偏移，在實驗中難以找到規律，還需進一步研究。

3.3 粘貼位置影響分析

以上分析主要關注了頻率相對較高的頻段，但這些頻段的局部密集峰過于密集，難以對粘貼位置的影響進行分析。圖6為1～10 kHz、10～20 kHz頻段PZT的導納曲線。為了更好地區分和對比，將編號C25的導納值整體減小了0.000 1 S，編號E16的導納值整體增加了0.000 1 S。

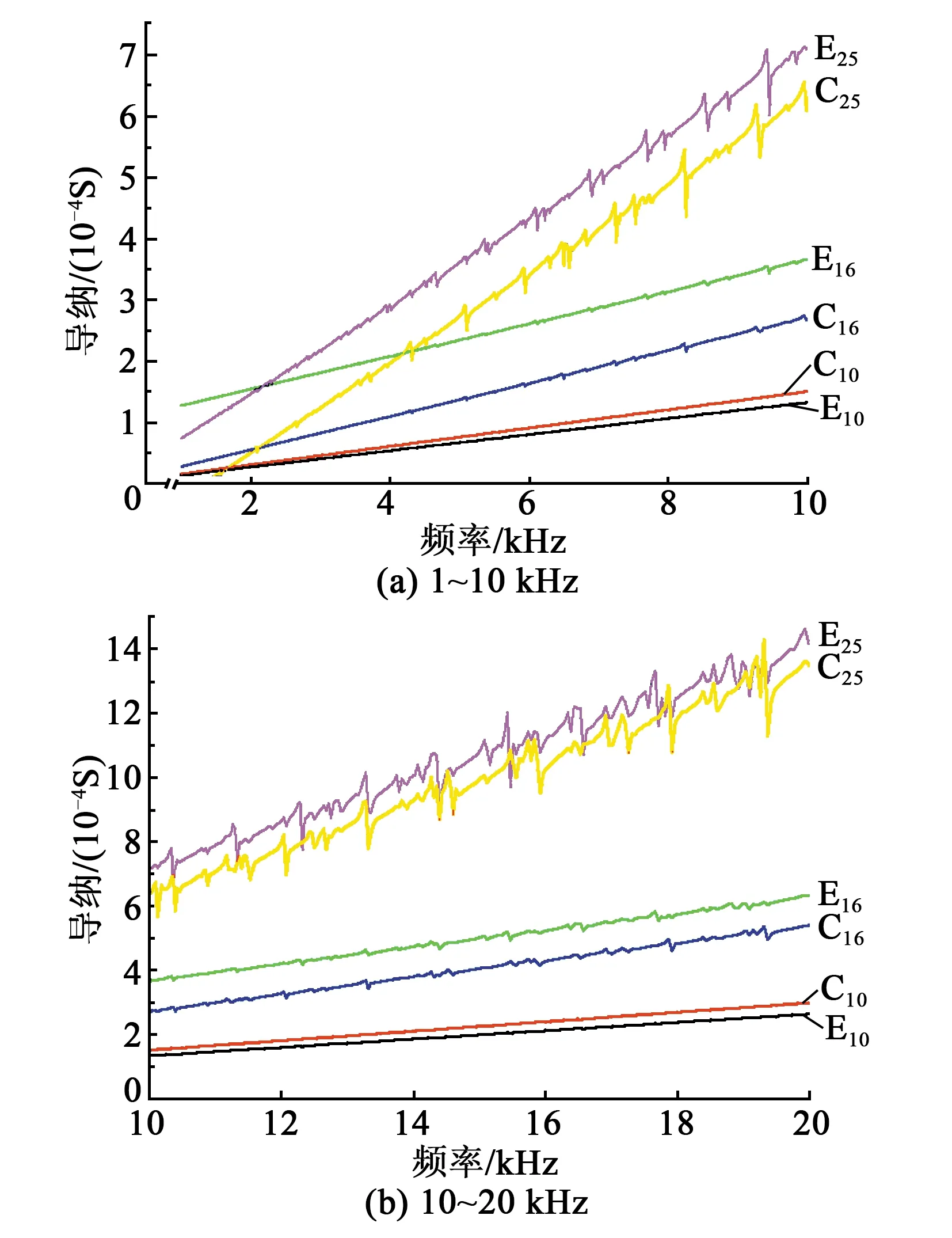
圖6 低頻段導納對比圖

由圖6可看出，在低頻段，PZT尺寸越大，局部密集峰越強。局部密集峰只出現在部分頻率段，這一點與高頻段完全不同。相同直徑的PZT片粘貼在近鋼板邊緣與近鋼板中心兩個不同的位置，其導納曲線上的局部密集峰出現的頻率段明顯不同。對比粘貼位置在鋼板的相同半徑位置，即不同直徑(如E25和E16、C25和C16)、相同粘貼位置的PZT出現局部峰的頻率段非常相似，且這種相似性在整個低頻段都存在。

綜上所述可知，結構的邊界對相同距離PZT片的導納影響相近，而對不同距離PZT片的導納將產生不同的影響。這主要是因為不同距離的邊界對相同聲波的影響不同造成的。也進一步印證了第2節中的理論分析，導納的變化受結構中聲波傳播的影響。粘貼位置影響的具體機理，因與聲波在結構中的傳播有關，是一個相對復雜的問題，需進一步研究。

4 結論

本文分析了PZT粘貼條件的導納模型和測量原理，通過設計對比實驗，研究了PZT尺寸和粘貼位置對PZT導納的影響，結論如下：

1) 粘貼后，PZT導納曲線上出現的局部密集峰攜帶有更多的結構信息，壓電阻抗法應優先選用包含大量局部密集峰的頻段。

2) 對于相同的結構，PZT片的尺寸越大，其諧振頻段局部密集峰的強度越大。應用壓電阻抗法時，在結合損傷尺寸等因素確定檢測頻段后，應該根據PZT粘貼后各階諧振頻率段的局部密集峰來決定PZT的尺寸大小。

3) 粘貼位置會影響局部密集峰的存在與強度。