煤層中斷層的透射槽波定量響應特征

王保利，金 丹，張喚蘭，程建遠

(1.中煤科工西安研究院(集團)有限公司，陜西 西安 710077;2.西安科技大學 地質與環境學院，陜西 西安 710054)

據統計，我國煤礦事故中由于地質構造原因引起的事故占比超過70%。我國煤礦地質構造復雜，開采地質條件較差，在這種情況下，未搞清工作面內的地質構造而貿然采掘，極易引發冒頂、片幫、壓架、突水以及瓦斯事故等，造成人員和經濟損失。因此，超前查明工作面內存在的隱蔽地質構造對煤礦安全高效生產至關重要。

影響煤炭開采的隱蔽致災地質因素主要包括：斷層、陷落柱、煤層厚度突變以及應力集中區等。準確、定量地查明這些地質異常體，可為安全高效回采提供地質保障，這也是我國煤礦高產高效地質保障系統的核心內容。

煤礦安全高效開采，迫切要求能夠超前、定量查明小斷層、煤層厚度變化、陷落柱、地應力集中區、瓦斯富集帶、裂隙發育帶等隱蔽致災地質因素。煤礦井下槽波地震探測技術已在采煤工作面內部隱伏構造探測方面取得了良好的地質效果，但是該技術尚無法實現斷層“三要素”(斷距、傾角、傾向)的定量判識和煤厚的直接測量，急需開展相關研究以攻克這一技術瓶頸難題。

由于槽波能量對斷層更為敏感、直觀，因此在斷層探測方面應用最為廣泛。大部分學者采用振幅衰減系數進行CT反演獲得采煤工作面內煤層連續性特征，并據此解釋斷層產狀；由于激發和接收的能量一致性問題，振幅衰減系數法反演精度較差，考慮到槽波的高頻和低頻分量在經過煤層內的異常構造時，其衰減快慢不一致，因此部分學者采用頻率譜相對透射系數法進行斷層的CT反演成像。楊元海提出了采用速度譜相對透射系數圖法來探測采煤工作面內斷層等地質構造，該方法具有原理簡單、易于實現且計算量小等特點；周官群等則利用槽波速度對采煤工作面內的斷層進行成像，通過速度相對高低來判定斷層性質(低速區為逆斷層，高速區為正斷層)，并指出斷層斷距可依據波速高低進行定性評價，或結合揭露區域類比進行定量評價。除了上述的透射槽波方法外，反射槽波也在斷層探測中得到了一定的應用。英國學者MASON等最早進行了一系列反射槽波探測斷層的試驗研究，并提出了延遲求和的斷層成像方法；HU和MCMECHAN提出了反射槽波逆時偏移成像技術，并用于模擬反射槽波成像；王季等提出了基于反射槽波頻散相似度的斷層成像方法，該方法充分利用了槽波的頻散性質,壓制了畫弧現象,有效提高了斷層成像的信噪比和分辨率；金丹提出了時窗能量比值的反射槽波成像方法，來提高反射槽波成像精度；王勃提出利用三分量槽波數據的極化偏移成像方法來消除斷層成像假象。梁森、黃超慧等研究了斷層的槽波響應特征,對不同斷距的斷層對槽波的能量和頻帶進行了半定量分析,但未給出斷距和能量之間的定量關系。

上述研究成果表明，在利用槽波進行斷層探測時，無論是透射槽波還是反射槽波，可獲得斷層的走向，并依據相對幅值大致判定斷距是否大于半煤厚，但尚不能定量地給出斷層斷距。同樣，在進行數值模擬和物理模擬時，也僅是從定性的角度討論斷層對槽波波場特征的影響，這使得槽波定量探測缺乏理論依據。筆者將從槽波數值模擬角度，分析不同斷距斷層的槽波波場響應特征，建立斷層斷距參數與透射槽波多屬性之間的定量關系，為斷層的透射槽波定量探測提供理論依據。

1 模型設計

為與實際模型更好對比，同時兼顧計算效率，設計的模型大小為544 m×240 m×96 m，包括了在6個面上各16 m的PML邊界層。網格采用1 m×1 m×1 m的正方體。

采用的3層模型參數見表1，其中頂板和底板參數一致，為了避免巷道對分析結果的影響，模型中沒有加入巷道；煤層埋深40 m(包括模型上部16 m PML邊界層)；設計的斷層位置在=200 m(包括模型左側16 m PML邊界層)，走向為方向，平面如圖1所示。

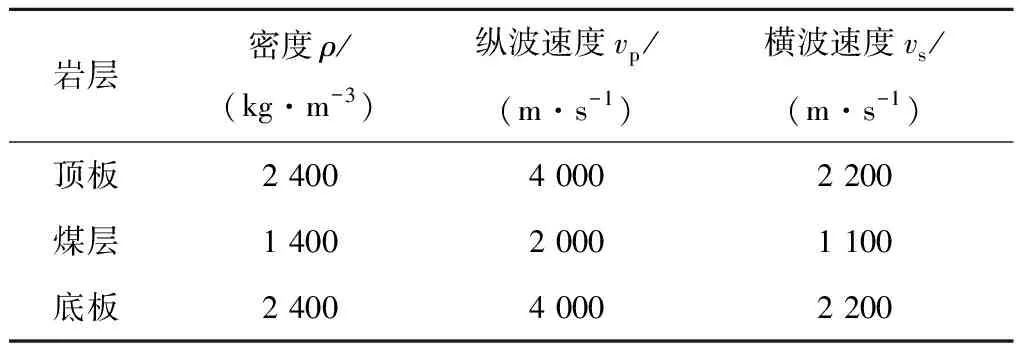
表1 含煤層3層模型物性參數

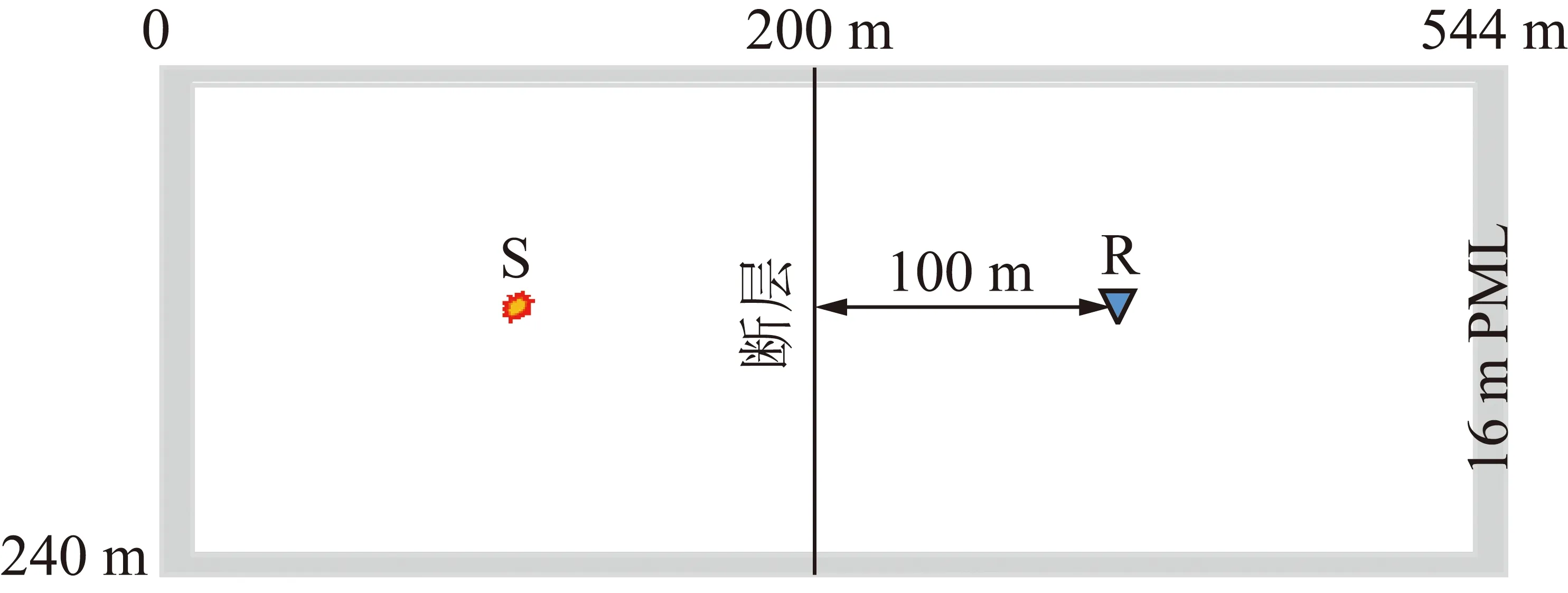
圖1 斷層模型XY平面

槽波探測斷層時，走向可以實現定量探測，但斷距難以定量，因此設計斷層時，其斷距參數的設定主要考慮斷距和煤厚的比例關系。具體設計的模型類型見表2，針對5 m煤厚和10 m煤厚的2種煤層分別設計0，1，2，3，4，5，6，8 m和0，2，4，6，8，10，12，16 m斷距的斷層模型16個，均為垂直斷層，斷距分別從煤厚的0倍，以0.2倍遞增到1.6倍，用以分析不同斷距的槽波波場響應。

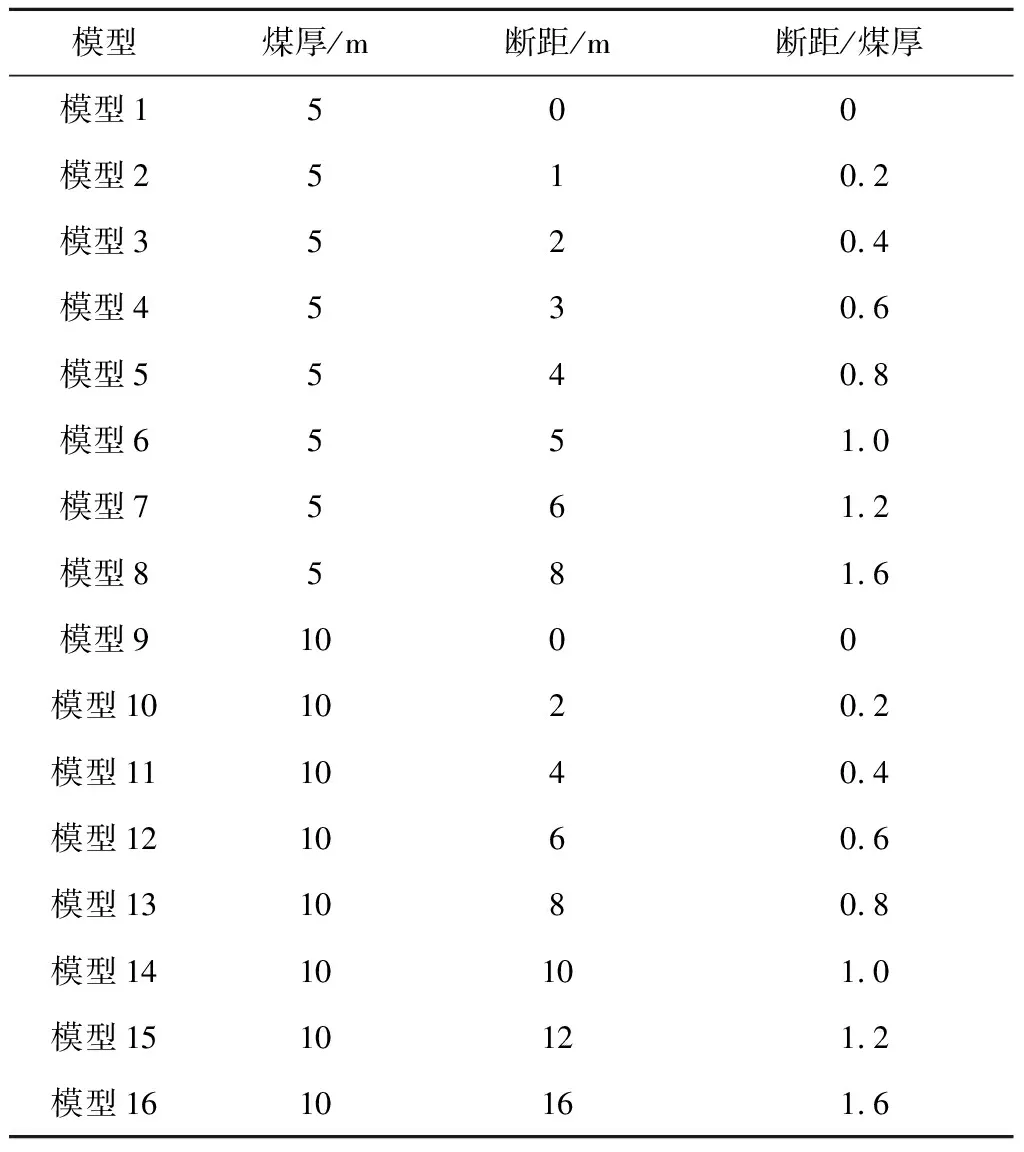
表2 斷層模型參數

2 三維三分量槽波數值模擬

利用三維一階應力-速度彈性波方程，采用二階時間八階空間的差分精度求解；同時為避免邊界反射對槽波波場的干擾，用PML對邊界進行處理；為同時能模擬Love槽波和Rayleigh槽波，采用漲縮源和剪切源2種震源加載方式；考慮到煤厚和槽波埃里相頻率的關系，對5 m和10 m煤厚的模型分別采用50～200 Hz和25～100 Hz的寬帶Ricker子波，振幅值固定為1.0，0.5 ms間隔采樣；為分析斷層對透射槽波的影響，在斷層左側100 m處布設震源點S，右側100 m處布設接收點R。

圖2為數值模擬得到的模型1和模型9的三分量記錄(三道依次為,和)，記錄顯示三分量記錄均有槽波發育，在記錄中屬于強優勢波場。利用多次濾波方法分別計算其群速度頻散譜(圖3)。圖3(a)分別為模型1(5 m煤厚)對應的三分量,,記錄，圖3(b)分別為模型9(10 m煤厚)對應的三分量,,記錄；圖3中分量頻散譜與理論計算的Rayleigh型槽波基階(黑線)和二階頻散曲線(白線)吻合、分量頻散譜與理論計算的Love型槽波基階(黑線)和二階頻散曲線(白線)吻合，由于炮檢連線平行于方向，因此槽波振型三分量分布與理論吻合；分量Love型和分量的Rayleigh型的基階能量明顯強于高階能量、分量頻散譜較為紊亂。

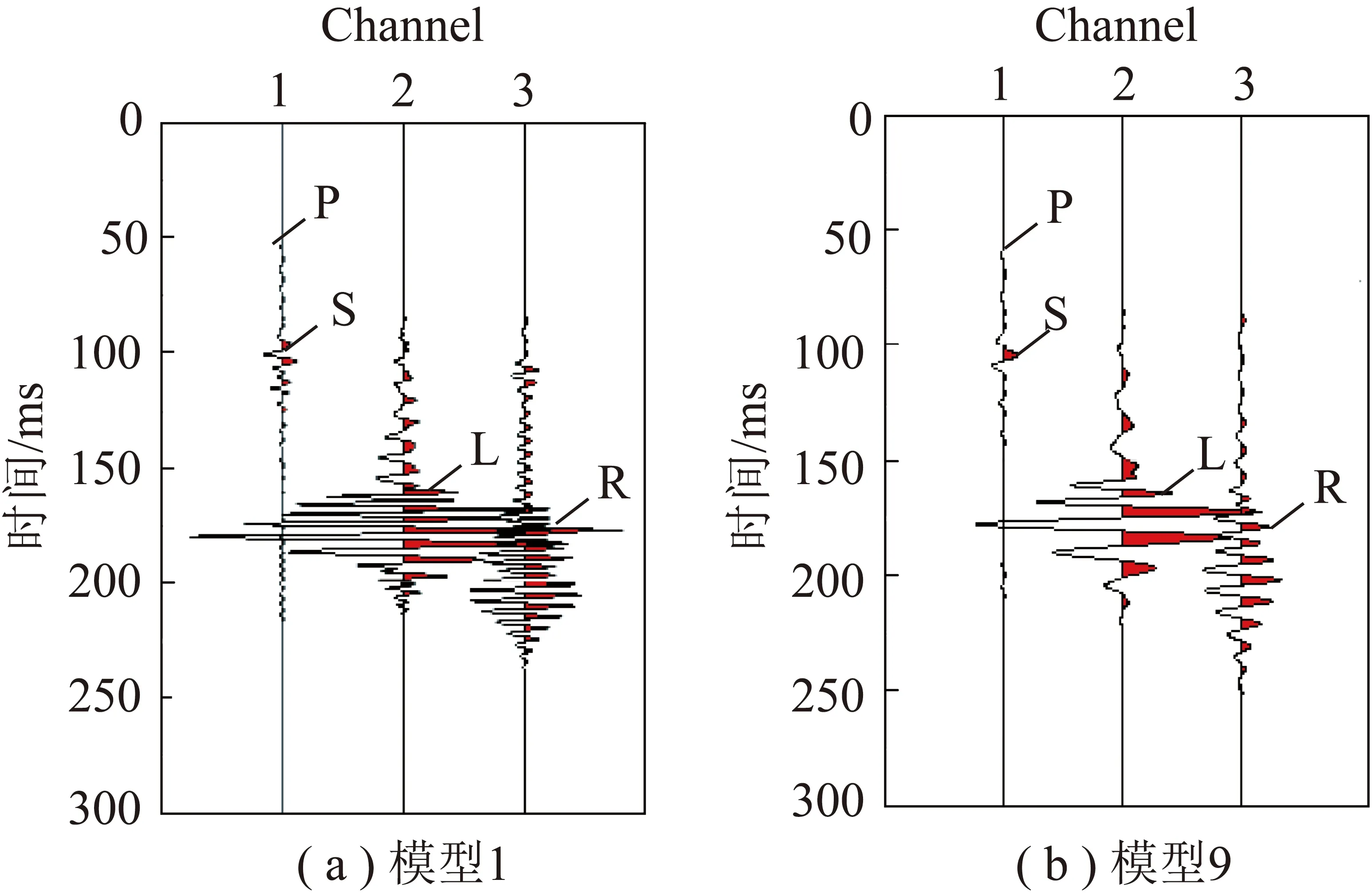
圖2 模擬得到的三分量記錄(依次為X,Y和Z)

根據上述分析，選定分量和分量記錄分別分析Love型和Rayleigh型的基階透射槽波對斷層斷距的響應特征。

3 不同斷距斷層的透射槽波響應特征

3.1 對透射槽波頻散曲線的影響

透射槽波在通過斷層時，如果對槽波速度產生影響，則該影響最終會體現在頻散曲線上，且不同斷距的斷層，對速度的影響規律同樣可在頻散曲線中分析得到。為此，筆者在通過對模型1～8(5 m煤厚)的不同斷距的透射Love型槽波和Rayleigh型槽波的頻散譜上拾取頻散曲線(圖4)，結果顯示：無論是Love型還是Rayleigh型槽波，頻散曲線幾乎沒有明顯有規律的變化(Rayleigh型槽波100 Hz處的變化應為基階和二階疊加所致，其位置如圖3(b)分量)。這表明，斷層(斷面垂直)不會對槽波的頻散特征造成影響，也即不會影響槽波傳播速度。

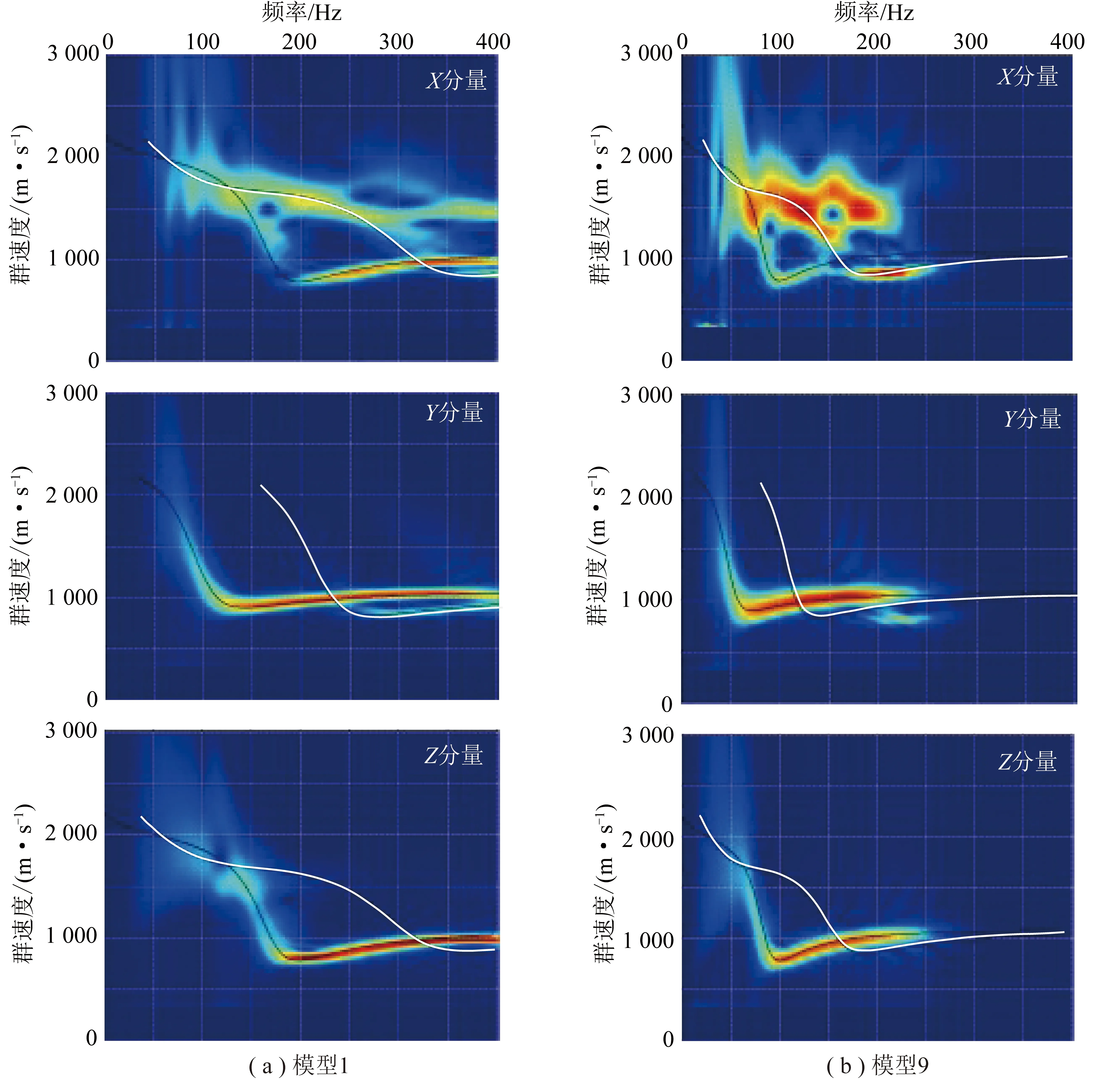
圖3 三分量記錄的頻散譜(黑色尾基階、白色二階)

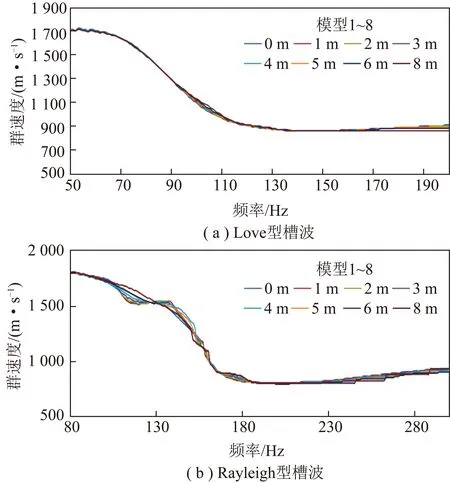
圖4 不同斷距斷層對透射槽波頻散曲線的影響

3.2 對透射槽波能量的影響

槽波探測煤層內構造的關鍵原理是因為煤層內部的構造(如斷層)會對槽波的傳播產生遮擋效應，從而改變槽波的能量；技術人員通過檢測槽波的能量變化獲得構造的位置及規模。因此斷層對槽波的能量的影響是必須進行精細討論的，特別是對斷層斷距的定量探測來說。

一般認為在斷層斷距大于煤厚時槽波會被完全擋住，從而無法接收到槽波。實際上，根據槽波在煤層深度方向上振幅分布特征，在煤層外側仍然有一定能量的槽波分布，這些槽波在遇到斷層時可以透射進入到斷層的另一段內繼續進行傳播(圖5)，特別是槽波低頻分量。

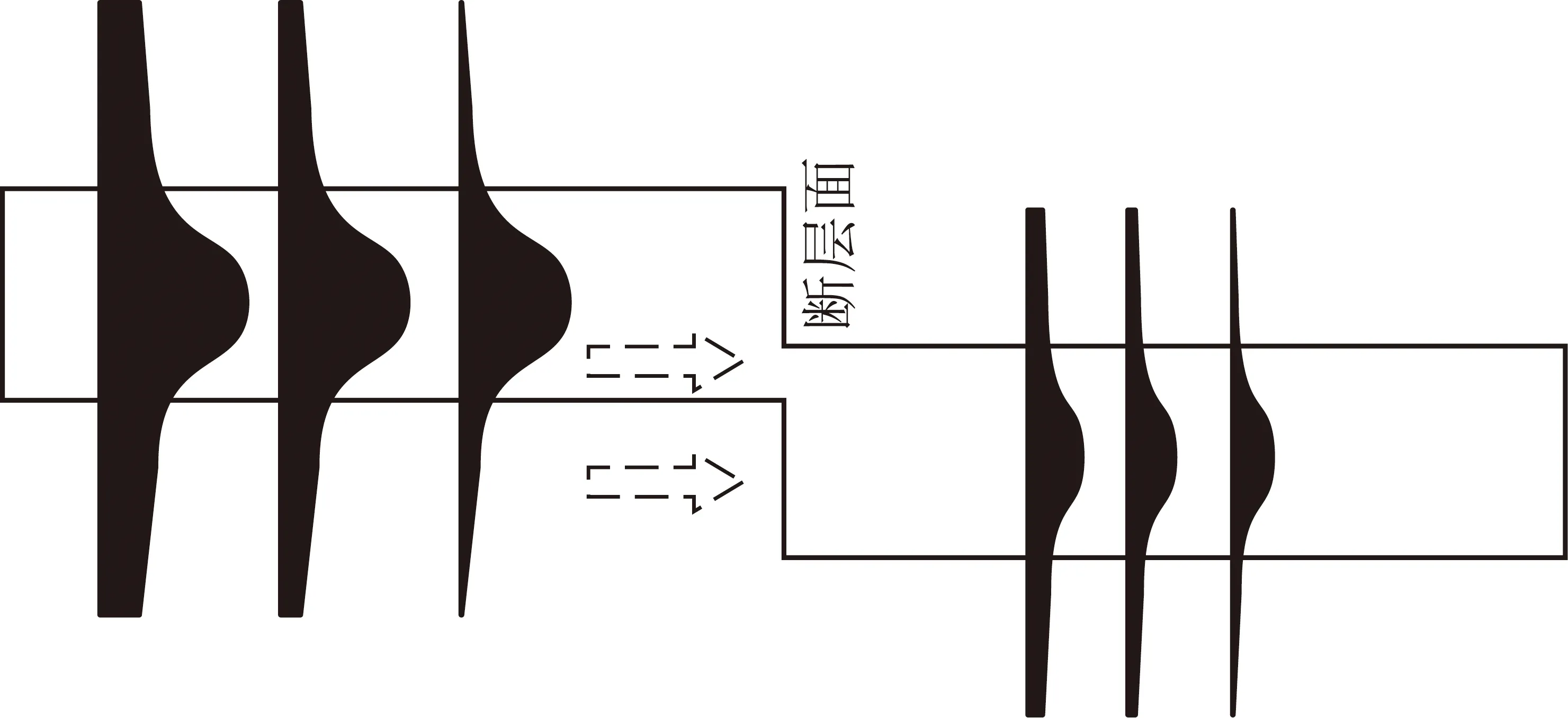
圖5 槽波通過斷層示意

筆者將在每個記錄的頻散譜上拾取了基階槽波頻散曲線對應槽波能量，并繪制出不同煤厚、不同斷距斷層模型中槽波的能量隨頻率的變化曲線，如圖6所示。

圖6(a),(c)的Love槽波振幅變化曲線顯示，5 m煤厚模型的頻率約為10 m煤厚模型的2倍，但振幅約為后者的一半，表明振幅的衰減與頻率有一定的關系；在圖6(b),(d)的Rayleigh型槽波也有這樣的現象，且兩者的振幅隨頻率變化趨勢非常一致，這表明斷距和振幅的衰減具有一定的定量關系。

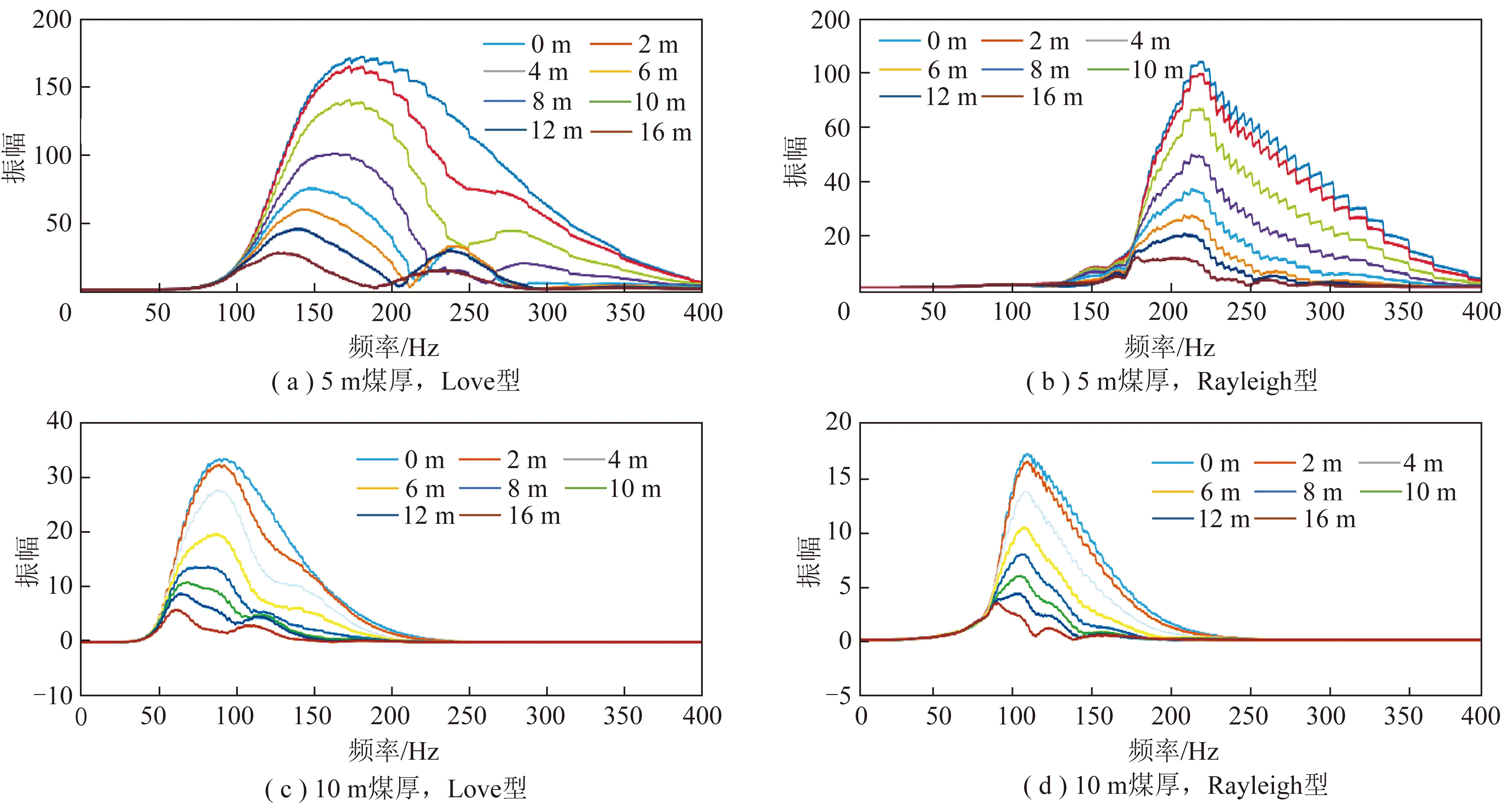
圖6 不同煤厚、不同斷距的斷層對槽波能量的影響

3.3 斷距對槽波振幅衰減的定量分析

前面定性地分析了不同煤厚、不同斷距的斷層對Love型和Rayleigh型基階槽波的影響，本節將進一步建立斷距與槽波能量的定量關系。槽波在過斷層時涉及模式轉換，理論推導相當困難，筆者主要基于理論記錄分析過斷層前后槽波能量的定量變化。

設定圖1中震源點S激發的信號用()表示，在沒有斷層存在的情況下(如模型1和模型9)，在接收點R接收到的槽波表示為

(,)=()e-ei

(1)

在斷層存在時，槽波穿過斷層使得能量發生變化，將斷層對槽波能量的這種衰減作用采用品質因子進行等效：

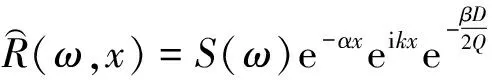
(2)

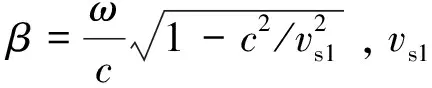
根據式(1)，(2)可得到斷層對槽波的影響：

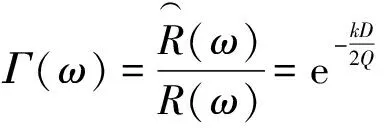
(3)

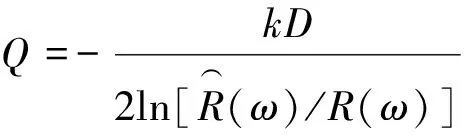
(4)

表2中的18個模型中，模型1和模型9分別為5 m煤厚和10 m煤厚無斷層模型，因此在計算時可作為式(4)中的()，從而計算出每個斷層模型Love型槽波等效和Rayleigh型槽波等效，如圖7所示：橫軸為波長/煤厚，可以消除煤厚的影響，從而將不同煤厚進行統一對比分析；為更精確分析能量衰減，分別選取Love型槽波和Rayleigh型槽波的埃里相之后，高階槽波到達以前的槽波，其中Love型槽波波長分析范圍為1.5～2.5，Rayleigh型槽波分析范圍為1.0～1.8，下限基本等于埃里相波長；對比發現，對同一類型的槽波，在=(為斷距，定義為規格化斷距)相同時，其衰減量基本相同；規格化斷距相同時，衰減量幾乎呈水平直線，表明與槽波波長(規格化后，即)無關；對比Love型，Rayleigh型的衰減發現，規格化斷距相同時衰減量也基本相同。

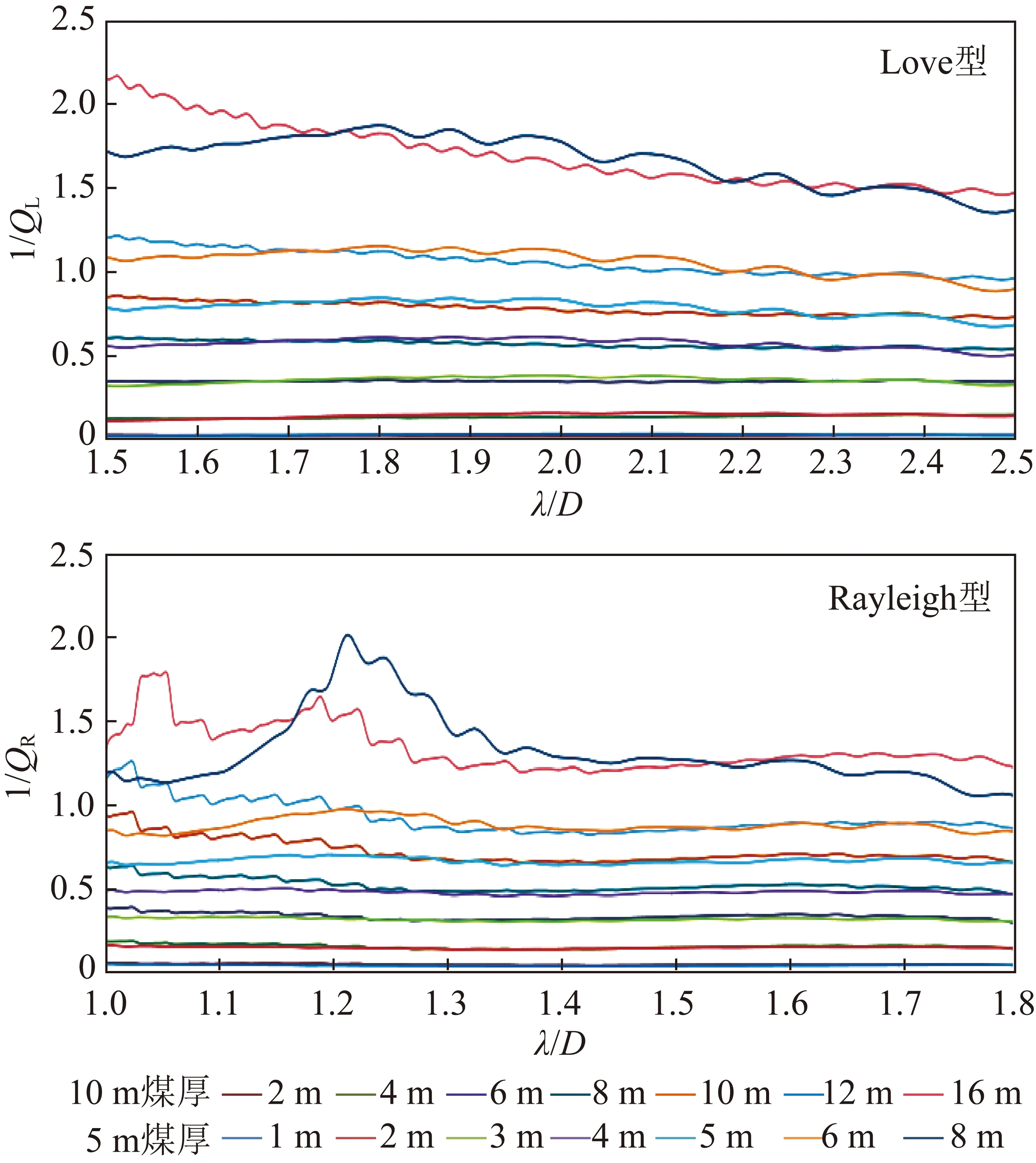
圖7 不同煤厚、不同斷距槽波衰減與波長的關系

在近似認為衰減量與槽波波長無關情況下，沿著圖7的橫軸，可求出不同煤厚、不同規格化斷距對應的等效(圖8)，分析可得：不同煤厚、相同振型的槽波，規格化斷距和等效具有相當好的一致性；Love型槽波和Rayleigh型槽波同樣具有很高的一致性，Love型槽波；隨著規格化斷距的增加，Love型槽波和Rayleigh型槽波的越來越小，表明其衰減量隨著規格化斷距的增大而增大；規格化斷距在=1/2(也即斷距為半煤厚左右)前后的變化呈現不同的斜率，在≤1/2時，等效隨規格化斷距呈現快速下降趨勢，而在>1/2時，以較緩的斜率線形下降，前后斜率差異達到8倍。

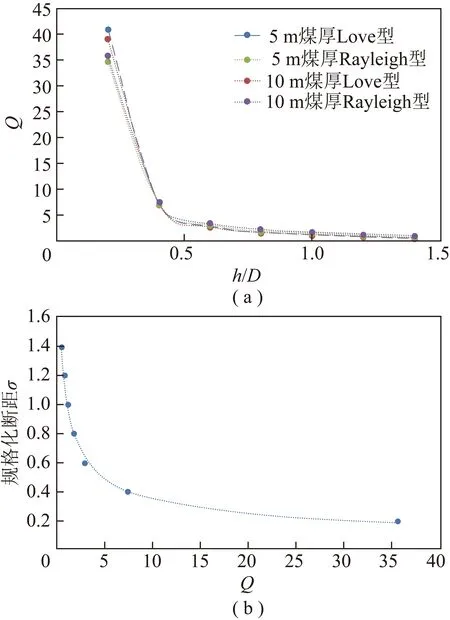
圖8 規格化斷距σ與等效Q定量關系

采用多項式擬合圖8(a)中的4條曲線的平均(擬合曲線如圖8(b)中虛線)，可得到規格化斷距與等效值之間的定量換算關系：

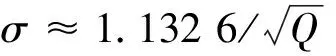
(5)

4 結 論

(1)垂直斷層不會影響槽波的頻散特征，只對槽波的能量有明顯的影響。

(2)模擬顯示，即便斷層斷距大于煤厚，仍然會有相當的槽波能量通過，特別是長波長分量。

(3)在槽波波長與煤厚相近時，相同規格化斷距的斷層對槽波的衰減量不隨槽波波長變化，且Love槽波和Rayleigh槽波衰減量幾乎相同。

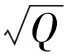
上述結論僅僅是基于理論模擬得出的，其用于實際勘探時仍需要進一步研究。下一步將研究如何在實際數據中應用本文提出的斷距定量關系式實現斷層斷距的定量探測。