關注審題能力培養 促進學習能力提升
湖南省攸縣第二中學
李雄飛 周春媛
提升審題能力在培養學生自主學習、獨立思考等學習能力上發揮著積極作用,然而部分師生在解題時常急于求成,習慣于生搬硬套原有模式,從而限制了思維品質和學習能力的提升.基于此,筆者從以下幾方面進行分析,以期引起同行對審題能力培養的重視.
1 審題時要仔細研讀隱藏于已知中的信息
審題時不僅要看清題目中的已知和結論,也應注意挖掘其中的內涵,注意文字語言和符號語言的提煉,從中解讀出有用信息進而認清問題的本質,找到正確的解題方向.在解題時,不能急于求成,應逐字逐句地仔細讀題,這樣可以有效地避免因審題不清而造成主觀臆斷的錯誤.在數學學習中,只有通過精讀和細讀才能找到解題的關鍵和要點,發現知識點間的區別和聯系,進而明晰考點,找到解決問題的突破口,從而順利解題.因此,教師在教學中要引導學生養成精讀、細讀的好習慣,通過長期的引導和滲透促使學生的思維更加嚴謹和全面.


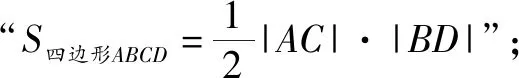
2 審題時要仔細觀察題目結構特征
仔細觀察、合理遷移是解題的重中之重.通過仔細觀察,學生根據問題的結構特點結合已有經驗進行合理猜想,找出問題的異同點,尋求問題的突破口,靈活應用相關概念、定理,將已知和結論建立聯系,進而根據題目特點進行合理遷移,達到解題的目的.

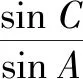
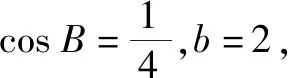
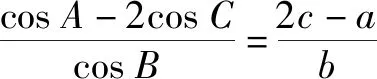
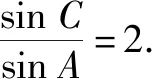
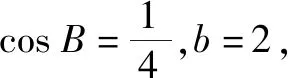


轉化思想既是學生應具備的基本數學思想,也是學生必備的基本能力,而合理的轉化需要扎實的基礎知識和靈活的數學思維.因此,在數學學習中,要多引導學生根據問題結構大膽猜測并實施合理的推導,不斷積累實踐經驗,促進解題能力和思維能力的提升.
3 審題時要關注問題本質
數學學習的過程不僅是知識積累的過程,更是自主學習能力提升的過程,故在數學教學中要摒棄傳統的“填鴨式”教學模式,引導學生學會自主學習和合作交流,通過合作、討論等學習活動培養學生批判性思維,對思維活動進行科學的檢查和評定,從而培養學生的創新能力.在審題時,學生應善于對已有信息進行整理和重組,找到有利于解題的信息,排除干擾,挖掘內在聯系,進而捕捉核心問題,找到問題本質,進而正確解題.
例3已知a,b是實數,函數f(x)=x3+ax,g(x)=x2+bx,f′(x)和g′(x)分別是f(x)和g(x)的導函數,若f′(x)g′(x)≥0在區間I上恒成立,則稱f(x)和g(x)在區間I上單調一致.
(1)設a>0,若f(x)和g(x)在區間[-1,+∞)上單調性一致,求b的取值范圍;
(2)設a<0,且a≠b,若在以a,b為端點的開區間上f(x)和g(x)單調性一致,求|a-b|的最大值.
解析:(1)由f′(x)=3x2+a,g′(x)=2x+b,根據f(x)和g(x)的單調性一致定義可知(3x2+a)·(2x+b)≥0在區間[-1,+∞)上恒成立.
由a>0,得3x2+a>0.故2x+b≥0,即b≥-2x在區間[-1,+∞)上恒成立,所以b≥2.
因此,b的取值范圍是[2,+∞).
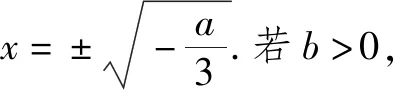
設b≤0.當x∈(-∞,0)時,g′(x)<0;


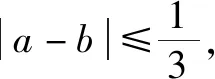

評析:本題為一道新穎別致的新定義題目,更能考查學生的綜合能力.在解此類問題時,學生不應著急解題,而應通過仔細審題,結合已有經驗進行新定義的剖析,從而理解和掌握新的定義.如,求b的取值范圍和|a-b|最大值時,都是運用f′(x)g′(x)≥0恒成立這一核心條件進行求解.因此仔細審題、合理剖析才是解題的關鍵所在.
總之,培養學生的審題能力,不僅有利于提升學生的解題能力,而且也有利于提升學生的思維能力.因此,教師要注重引導和滲透,使學生會審題、善思考,進而將其培養成具有獨創精神的創新人才.

