精心組織教學活動 促進核心素養提升
——以“函數與方程(一)”為例

江蘇省海門中學

姜璐璐

數學教學應堅持以生為本，引導學生通過觀察、發現、歸納等數學活動掌握基本知識和基本技能，在解決問題的過程中形成經驗，從而在知識和經驗的共同作用下形成學習能力.筆者在“函數與方程(一)”教學時，借助情境和問題設計教學活動，在培養學生觀察能力、概括能力、抽象能力等方面取得了較大突破，與大家分享，以期共鑒.

1 教學分析

“函數與方程(一)”是一節抽象的概念課，重點是理解和掌握函數零點定義及零點存在性定理.概念課看似簡單，但受傳統教學模式影響，在教學中常出現“重結論，輕過程”的現象，從而將“概念課”變成了“習題課”，學生知道個一知半解就忙著去應用，結果后期解決綜合性問題時漏洞百出.要讓學生真正將概念學懂吃透，既清楚內涵又了解外延，需要教師精心預設.本節課在問題情境的引領下，旨在培養學生的觀察、抽象概括能力，體驗函數與方程、轉化與化歸、數形結合等重要數學思想的應用，從而提升數學核心素養.

2 教學活動設計

2.1 回顧舊知，引出新知

教學片段1：

師：利用對數知識求方程0.84x=0.5的近似解，該如何求呢？

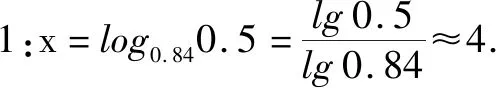
師：很好！如果利用圖象，你能求嗎？

生2：可以求.將方程0.84x=0.5左右兩邊看作兩個函數，y=0.84x和y=0.5，兩函數y=0.84x和y=0.5圖象交點的橫坐標即為所求.

師：很好.生2通過構造法構造了兩個較為熟悉的函數y=0.84x和y=0.5，這樣在同一直角坐標系中作出函數圖象，借助圖象可求方程近似解.

設計意圖：函數與方程都是高中數學重點內容，在數學中占有重要的位置，同時兩者又有著緊密的聯系.如果教學之初就直接指出兩者的聯系似乎有些生硬，為此，先用舊知“對數相關知識”來引入，引導學生用代數的思路直接求解.接下來，運用問題“如何利用圖象求解”，引導學生聯想函數，由此將方程轉化為了函數，這樣引入新課題也就水到渠成了.

2.2 借助特例，歸納提煉

教學片段2：

師：觀察以下幾個特殊函數的圖象，試寫出函數圖象與x軸交點的坐標，并求出對應方程的根，看看你有哪些發現.

①一元二次方程x2-2x-3=0與函數y=x2-2x-3(圖象如圖1)；

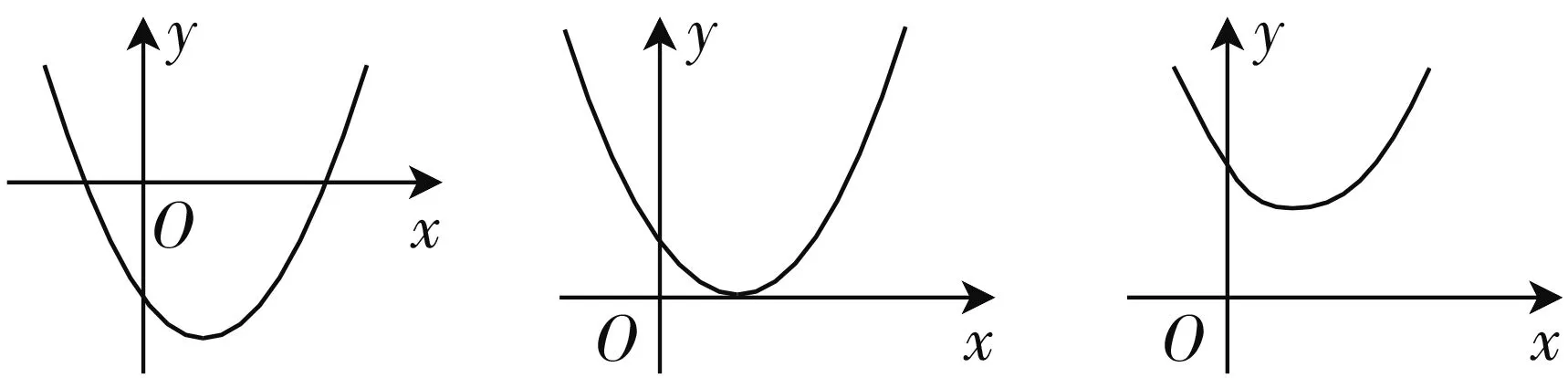
圖1 圖2 圖3

②一元二次方程x2-2x+1=0與函數y=x2-2x+1(圖象如圖2)；

③一元二次方程x2-2x+3=0與函數y=x2-2x+3(圖象如圖3).

問題給出后，教師預留時間讓學生進行觀察，并引導學生應用數學語言進行總結和歸納，很快，很多學生迫不急待的想發表自己的見解了.

生3：分析第①組，該一元二次方程有兩個根，分別為-1和3，與之相應的函數圖象與x軸的交點坐標分別為(-1，0)，(3，0).由此可知，方程x2-2x-3=0的根即為函數y=x2-2x-3與x軸的交點的橫坐標.

生4：在第②組中，方程的根為x1=x2=1，相應的交點坐標為(1，0)，故與生3得出的結論類似.

生5：在第③組中，方程沒有實數根，圖象與x軸無交點.

師：大家說得非常好！剛剛我們觀察的是特殊方程，如果對于一般方程會有怎樣的結果呢？請各小組分工協作，完成下面表格(如表1).(學生已經發現了一般規律，很快完成了表格的填寫.)

表1 一元二次方程與對應函數的關系

注：a>0.

師：各小組表格都已經填寫好了，現在請結合表格內容歸納總結，一般一元二次方程ax2+bx+c=0(a≠0)的根與二次函數y=ax2+bx+c(a≠0)的圖象有什么關系.

生6：一元二次方程ax2+bx+c=0(a≠0)的實數根就是二次函數y=ax2+bx+c(a≠0)的函數值y=0時自變量x的值，也就是二次函數y=ax2+bx+c(a≠0)的圖象與x軸交點的橫坐標.

師：很好！一般地，把使函數y=f(x)的值為0的實數x稱函數y=f(x)的零點，即方程f(x)=0的實數解叫做函數y=f(x)的零點.

設計意圖：為了便于觀察、計算，教師設計了幾個簡單的一元二次方程，通過方程的根與對應函數圖象與x軸交點坐標相對比，得出了一元二次方程的根即為相應的一元二次函數圖象與x軸交點的橫坐標.結論得出后，為了將其轉化為一般規律，教師讓學生聯想一般方程，完成了從特殊到一般的轉化.在此基礎上給出函數零點定義也就使定義更加具體形象了，學生也更容易總結歸納三者的關系：方程f(x)=0有解?函數y=f(x)的圖象與x軸有交點?函數y=f(x)有零點.這樣讓學生經歷由根到交點再到零點的過程，有利于培養學生的邏輯思維能力.

2.3 借助轉化，檢驗應用

教學片段3：

例1求證：二次函數y=2x2+3x-7有兩個不同的零點.

證法1：(代數法)考察二次方程2x2+3x-7=0，因為Δ=32-4×2×(-7)=65>0，所以方程2x2+3x-7=0有兩個不等的實數根.因此，二次函數y=2x2+3x-7有兩個不同的零點.

證法2：(幾何法)由f(x)=2x2+3x-7的二次項系數是2，可知拋物線的開口向上，且f(1)=2+3-7=-2<0，所以二次函數y=2x2+3x-7與x軸有兩個交點.因此，二次函數y=2x2+3x-7有兩個不同的零點.

例2判斷函數f(x)=x2-2x-1在區間(2，3)內是否存在零點.

設計意圖：在教學中，為了實現知識的內化，了例題環節.設置例1引導學生從不同角度思考零點問題，即代數法和幾何法.對于例2，根據學情可知，在解決此類問題時多數學生習慣運用代數法來求解，教師可以順勢引導學生通過尋找“另外方法”為下面的教學內容作鋪墊，讓學生的思維在問題的引導下螺旋上升.

2.4 完善猜想，形成定理

教學片段4：

師：觀察例2中函數f(x)=x2-2x-1的圖象，我們猜想出“若函數y=f(x)在區間(a，b)內有零點，則必有f(a)f(b)<0”.如果這樣說你們認為成立嗎？“若函數y=f(x)在區間[a，b]上有f(a)f(b)<0，則函數y=f(x)在區間(a，b)內一定有零點”呢？

設計意圖：通過創設問題引發學生對定理成立條件的關注，從而為定理的引入及內化作好鋪墊.在教學中，可繼續引導學生聯想特例來驗證，這樣學生更容易理解“不間斷的曲線”這一限定條件.接下來還可以提出問題①在什么條件下，可以使函數y=f(x)有唯一零點？②為什么題設中是閉區間[a，b]，而結論中是開區間(a，b)？這樣，通過仔細推敲和挖掘，讓學生對定理的理解更加細致、全面，為后面的應用奠定堅實基礎.

3 教學反思

本節課通過前期的鋪墊，利用“函數與方程”“數形結合”等重要數學思想方法引發了學生對“函數零點”的思考，從而將方程的根、圖象與x軸的交點、函數零點緊密相連，實現了代數與幾何之間的轉化.接下來又圍繞“函數零點定理”經歷了一次探究之旅，從觀察、發現、猜想、推理、驗證、應用等環節突破了重難點，發現了問題的本質，最終形成了定理.數學定理本是抽象的，為了提升教學的有效性，發展學生的數學思維，在教學中需要多從學生的認識角度去思考問題，通過創設有價值的問題引導學生在知識的梳理、歸納、總結等數學活動中建立完整的知識體系，進而提升解決問題的能力.

總之，要發揮課堂教學價值，離不開教師精心的預設.只有精心預設才能使知識向正方向遷移，從而揭示問題的本質，提煉出有價值的數學方法，最終形成解題能力和學習能力，提高數學核心素養.