題源探秘 多解思維 變式拓展
——一道零點存在性問題的探究
浙江省紹興市上虞區城南中學
方鎮軍
涉及函數零點的存在性問題是歷年高考數學試題中的熱點與難點問題之一,每年高考試卷上都有其熟悉的影子.巧妙地把函數零點與存在性這兩個重點問題加以融合,創新新穎,變化多端,同時又可以很好融合其他相關的數學知識,有效考查考生的數學知識、數學思想方法與數學能力等,具有較好的高考區分度與選拔性,一直備受命題者青睞.
1 問題呈現
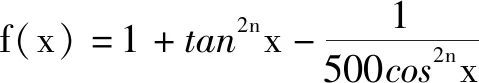
此題以函數零點的存在性為問題背景,交匯并融合三角函數、不等式、函數的最值以及函數的零點等眾多知識,題目簡單明了,創新新穎.抓住函數本質,利用函數零點的存在性加以突破,可以通過導數思想,換元、重要不等式等思維巧妙切入,利用導數法或重要不等式法來處理,進而得以破解.
2 問題破解
思維視角一:導數思維.
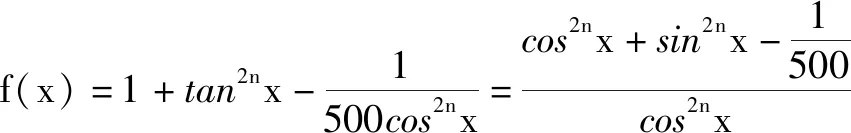
故填答案:10.
點評:根據函數的零點存在性問題對函數的解析式加以變形,等價轉化并合理構造對應的函數.利用導函數的零點的確定與求解來轉化與確定所構造函數的最小值,進而根據題目條件建立相應的指數不等式,結合正整數n來確定其最小值.導數法直接處理,目的明確,只是運算量大,過程繁雜.
思維視角二:換元思維.
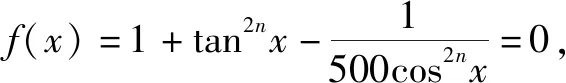
故填答案:10.
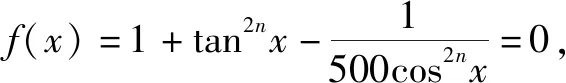
故填答案:10.
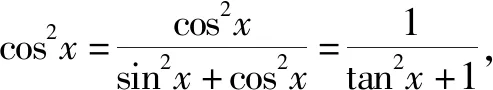
故填答案:10.
點評:根據函數解析式的特征,借助正弦換元、均值換元或正切換元等方式引入參數;結合函數的構造,通過求導,利用導數及其應用來確定函數的最小值;根據指數不等式的求解,以及正整數n來確定其最小值問題.換元是手段,簡化關系式、求導是目的.不同的換元處理,有不同的解題功效.
思維視角三:重要不等式思維.
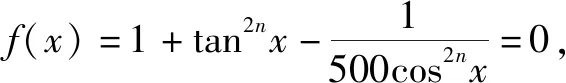
故填答案:10.
點評:根據函數的零點存在性問題加以變形,結合三角關系式的合理轉化,利用權方和不等式確定三角關系式的最小值,進而根據題目條件建立相應的指數不等式,通過不等式的求解,以及正整數n來確定其最小值問題.借助權方和不等式轉化確定最值是破解的關鍵所在,只是該不等式對大部分考生來說比較陌生,只是作為一個了解.
3 題源探秘
根據原問題的分析與破解,其實質是求解函數f(x)=sin2nx+cos2nx的最小值問題,巧妙利用函數零點的存在性以及指數不等式加以進一步地融合、提升與拓展.回歸本質,探秘題源.
問題(2010年全國高中數學聯賽福建省賽區預賽第7題)函數f(x)=sin2kx+cos2kx(k∈N*)的最小值為______.
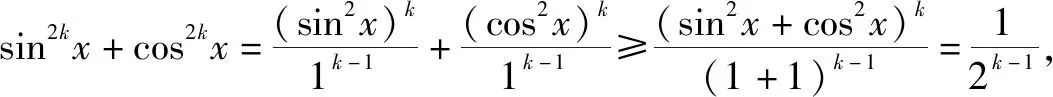
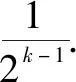
點評:對比高中數學聯賽問題,破解時直接借助權方和不等式,可以更加快捷地處理該問題.而對一般考生來說,利用導數法或換元法處理也同樣可以求解,這里不多贅述,可以參考原問題的解析過程求解.
4 解后反思
涉及函數零點的存在性問題是相關的數學知識、數學思想方法和數學關鍵能力等方面交匯與融合的一個很好場所,破解的基本思路是進行合理的等價轉化,變形為相應的方程、對應的代數式、函數的解析式等,通過方程思想、代數式的不等式處理、函數的圖象與性質、導數法等來分析與處理.破解此類問題要求具備比較高的化歸與轉化能力、邏輯推理能力等,同時對創新意識與創新應用等方面都有較高的要求.

