透過題干抓本質 類比推理巧解題
白銀市第一中學
高曉藝
1 問題提出
類比推理也稱類比法.在人教A版選修1-2中第二章推理與證明中有系統詳細的介紹.類比推理是培養和提升學生邏輯推理素養的重要的知識載體.而在教學過程中,我們發現學生在應用類比推理解題時往往存在思維過程無法落地的困惑.僅僅追求所得結論與題干已知結論的“形似”,而忽略了類比的本質“神似”.從而導致了對一些較為復雜的問題無從下手求解.
實際上,在進行類比推理時,我們所需要的核心并不是結論的一致性或者相似性,而是透過現象看本質,挖掘在解題過程中對本質思想或方法的類比過程.
本文中將結合幾個利用類比推理思想來求解的具體案例進行實踐和反思.
2 教學案例

請你類比上述方法,計算1×2×3+2×3×4+……+n(n+1)(n+2)的結果.
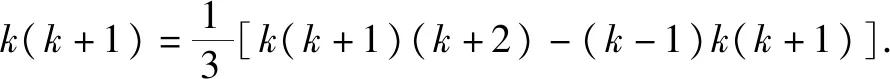
解:依題意可得
由此可得
…………
以上n個式子相加,得
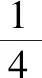
問題推廣1:
“計算1×2×3×4+2×3×4×5+……+n(n+1)(n+2)(n+3)的值.”[1]

問題推廣2:
求12+22+32+……+n2的值.

=1×2+2×3+……+n(n+1)-(1+2+……+n)

A.714 B.1870 C.4895 D.4896

解:由an+1=an+2-an,得

例3在等差數列{an}中,若a10=0,則有a1+a2+……+an=a1+a2+……+a19-n(n<19,且n∈N*)成立.類比上述性質,在等比數列{bn}中,若b9=1,則存在怎樣的等式?
分析:等差數列與等比數列由于具有相似的定義和性質而經常進行類比.首先分析題干本質,在等差數列中,由a10=0,易知,an+a20-n=0,即an+1+a19-n=0,故an+1+an+2+……+a19-n=0,因此有結論a1+a2+……+an=a1+a2+……+a19-n成立.那么類比到等比數列中,由b9=1,得bn·b18-n=1,即bn+1·b17-n=1,因此bn+1·bn+2……b17-n=1,故可類比推理得出相應的性質b1·b2……bn=b1·b2……b18-n(n<18,且n∈N*).
解:在等比數列{bn}中,若b9=1,則有b1·b2……bn=b1·b2……b18-n(n<18,且n∈N*).


圖1
分析:首先分析題干中“黃金橢圓”的離心率求解過程,進而類比求解“黃金雙曲線”的離心率.其實質依然是求解過程及思路的類比,是思想方法的遷移.

3 教學反思
開普勒曾經說過:“我珍視類比勝過任何別的東西,它是我最可信賴的老師,它能揭示自然界的秘密.”的確,我們經常應用平面幾何的結論去類比推理得到空間幾何中的一些結論,也會不斷地將等比數列與等差數列進行類比學習.在教學過程中,我們也經常應用類比已有知識的形成過程去習得新知.比如,在學習“數學歸納法”這一內容時,就會類比多米諾骨牌游戲的原理,從而容易理解數學歸納法的證明原理.類比推理為我們獲得新知識和新結論提供了方向和思路,也是我們解題中不可或缺的好幫手.在日常教學過程中,教師應該重視對學生類比推理思維的培養.這個培養不是通過一道題或者一堂課就能做到的,而應該是一個不斷滲透,慢慢形成的過程.教師在具體的解題教學過程中,應該重視對類比過程的分析和引導,鼓勵學生抓住問題的本質去進行類比,尤其是在思想方法的類比過程中,應該重視舉一反三,重視變式練習和對問題的推廣應用.只有在由易到難不斷應用的過程中,才能逐漸培養和提升學生的邏輯推理素養.

