巧借常值數列 妙破數列問題
四川省成都市第七中學
廖學軍
常值數列是一類特殊的數列,是等差數列與等比數列的一個和諧統一.常值數列中各項的值都相等,其通項公式是an=a1=a(n∈N*,a∈R),是一個公差d=0的等差數列,當a≠0時其又是一個公比q=1的等比數列.常值數列在解題過程中往往有其特殊的作用,特別在一些相關的數列問題中,常值數列的特征不明顯,經過合理的變形、轉化與推導,“添油加醋”才能選取、配湊或構造出對應的常值數列,進而借助常值數列的相關特征性質來處理與解決問題,往往能起到非常良好的效果,出奇制勝,簡單快捷處理相應的數列問題.
1 巧選常值數列
根據題目條件,選取滿足條件的特殊數列——常值數列,進而利用常值數列的特征性質來分析、處理與解決問題.
例1已知等差數列{an}的前n項和為Sn,若a3+a5+a7=24,則S9等于( ).
A.288 B.144 C.72 D.36
分析:結合題目條件,通過選取特殊數列——常值數列,使一般性的等差數列問題特殊化,進而在特殊情況下加以運算,再對特殊情況下常值數列的運算結果進行一般化處理即可得以快捷求解.
解析:不妨設等差數列{an}的公差為0,此時數列{an}是一個常值數列,則由a3+a5+a7=24,可得a1=an=8,所以S9=9a1=9×8=72.
故選:C.
點評:通過特殊的常值數列的選取與引入,可以非常快捷地處理一些與數列運算有關的通項、求和等問題.通過常值數列等特殊數列的選取,將一般性的數列問題特殊化,使問題簡單統一化,簡化運算.
2 巧判常值數列
根據題目條件,準確判斷出滿足條件的數列為特殊數列——常值數列,直接利用常值數列的特征性質來分析、處理與解決問題.
例2(2014年高考數學安徽卷理科第12題)數列{an}是等差數列,若a1+1,a3+3,a5+5構成公比為q的等比數列,則q=______.
分析:利用兩個等差數列對應的項依次相加后得到的數列還是等差數列的性質,可以判定a1+1,a3+3,a5+5構成一個等差數列,其同時又是一個等比數列,得以判定其是一個常值數列,再利用其特征性質來確定公比的值.
解析:因為數列{an}是等差數列,而1,3,5也是一個等差數列,所以a1+1,a3+3,a5+5構成一個等差數列.又a1+1,a3+3,a5+5構成公比為q的等比數列,所以a1+1,a3+3,a5+5是一個常值數列,則有q=1.
故填答案:1.
點評:利用“非零常值數列既是等差數列又是等比數列”這一基本性質,進而結合一個數列滿足既是等差數列又是等比數列這一性質特征來判定其是常值數列,則知其公差d=0,公比q=1.綜合等差數列的性質,巧妙判斷,合理應用,快捷求解.
3 巧用常值數列
根據題目條件,巧妙選用滿足條件的特殊數列——常值數列,為進一步利用常值數列的特征性質來分析、處理與解決問題提供條件.
例3設數列{an},{bn}都是等差數列,且a1=20,b1=80,a10+b10=100,則a2020+b2020等于( ).
A.2020 B.100 C.50 D.無法確定
分析:結合條件列出關系式(a10+b10)-(a1+b1)=0的確定,綜合等差數列的性質得以判定滿足cn=an+bn的數列{cn}為常值數列,進而利用常值數列的性質特征來確定對應通項的值即可.
解析:由于(a10+b10)-(a1+b1)=100-(20+80)=0,則知滿足cn=an+bn的數列{cn}是一個常值數列,所以c2020=a2020+b2020=a10+b10=100.
故選:B.
點評:結合“一個公差為0的等差數列”為常值數列這一基本性質,利用常值數列的各項的值都相等這一性質特征來確定對應通項的值問題.巧妙應用常值數列,合理轉化,快捷求解.
4 巧湊常值數列
根據題目條件,通過合理配湊得以確定滿足條件的特殊數列——常值數列,為進一步利用常值數列的特征性質來分析、處理與解決問題奠定基礎.
例4(2018年北京大學自主招生數學試卷第10題)設數列{an}的首項a1=2019,前n項和Sn=n2an,則a2018的值為( ).
分析:根據題目條件進行消元處理,把涉及通項an與前n項和Sn的關系式轉化為只含有通項an的關系式(n+2)an+1=nan,借助配湊思維,合理添加相應的系數n+1轉化為(n+2)(n+1)an+1=(n+1)nan,結合常值數列的判定與性質來確定對應的通項an.
解析:由Sn=n2an,得Sn+1=(n+1)2an+1.
以上兩式對應相減,可得
Sn+1-Sn=(n+1)2an+1-n2an.
即an+1=(n+1)2an+1-n2an,化簡可得
(n+2)an+1=nan.
上式兩邊同時乘n+1,可得
(n+2)(n+1)an+1=(n+1)nan.
則數列{(n+1)nan}是一個常值數列,所以
(n+1)nan=2×1×a1.
即
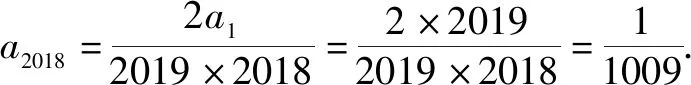
故選:C.
點評:結合條件的合理配湊來確定“an+1=an”這一特征關系式,進而確定一個常值數列,為進一步解決數列通項等相關問題奠定基礎.通過合理配湊,結合常值數列的判定,合理利用常值數列的性質,為數列相關問題的破解開辟一個新局面.
5 巧構常值數列
根據題目條件,通過合理的變形、轉化與推導,構造滿足條件的特殊數列——常值數列,再結合常值數列的特征性質來分析、處理與解決問題.
例5已知數列{an}滿足an+1=2an+3×5n,a1=6,則數列{an}的通項公式為an=______.
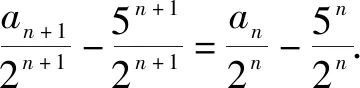
解析:由an+1=2an+3×5n,可得an+1-5×5n=2an-2×5n,則有an+1-5n+1=2(an-5n).
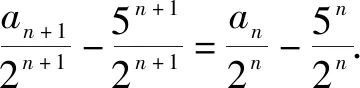
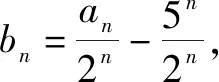
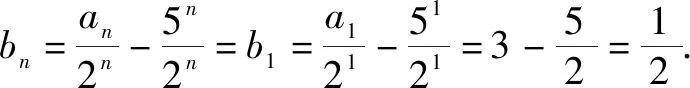
故填答案:2n-1+5n.
點評:結合數列遞推關系式的變形與轉化,并合理構造新數列,通過常值數列“an+1=an”這一特征關系式來判斷與應用,為求解復雜的數列通項公式提供條件.合理構造常值數列來解決問題,可以有效簡化解題過程,減少運算量.
在破解一些數列問題時,結合對題目中已知的數列遞推關系式等條件加以變形、轉化與推導,通過特殊選取、準確判斷、有效選用、合理配湊、巧妙構造等技巧,“慧眼識英雄”,挖掘常值數列的影子.結合整體思想與目標意識,利用直覺思維、邏輯推理與敏銳的眼光,從而選取、識別或導出相應的常值數列,進而利用常值數列的特征性質加以解題,往往能出奇制勝,快速破解.

