基于分形理論的粗糙齒面齒輪動力學(xué)研究

謝磊，李政民卿

(南京航空航天大學(xué)，直升機傳動技術(shù)國家級重點實驗室，江蘇南京 210016)

0 前言

齒輪傳動具有傳動精確、平穩(wěn)、高效以及結(jié)構(gòu)緊湊和承載能力大等優(yōu)點，被廣泛應(yīng)用于汽車、船舶和航空等領(lǐng)域。近年來，齒輪動力學(xué)仍是齒輪相關(guān)領(lǐng)域的研究熱點，許多國內(nèi)外學(xué)者針對齒輪的動力學(xué)特性，考慮時變嚙合剛度、誤差、齒側(cè)間隙和齒面摩擦等因素,展開了大量研究并取得了豐碩的研究成果，為進(jìn)一步深入研究齒輪動力學(xué)奠定了良好基礎(chǔ)。

在考慮誤差的齒輪動力學(xué)研究中，BONORI和PELLICANO建立了包含隨機加工誤差的齒輪動力學(xué)模型，分析了隨機分布齒廓誤差對動力學(xué)的影響；INALPOLAT等研究了以周節(jié)誤差引起的長周期準(zhǔn)靜態(tài)傳遞誤差為主要激勵的齒輪動力學(xué)特性；WANG和ZHANG將傳遞誤差分解為諧波分量與隨機分量，提出了考慮隨機誤差的齒輪系統(tǒng)動態(tài)分析模型；常樂浩等研究了齒輪綜合嚙合誤差的計算方法及它對系統(tǒng)振動的影響；石照耀等提出了齒輪副整體誤差的概念與獲取方法，研究了考慮整體誤差的齒輪動力學(xué)行為；黃康等人基于分形理論研究了粗糙度影響下的齒輪非線性動力學(xué)行為，但模型為簡化較多的純扭轉(zhuǎn)模型。現(xiàn)有研究表明，齒面微觀形貌會對誤差產(chǎn)生較大影響，但現(xiàn)有齒輪動力學(xué)研究中常因粗糙齒面的復(fù)雜性而忽略其影響，且在研究時多未考慮摩擦這一重要因素，研究尚不全面。

針對上述問題，為剖析粗糙齒面對齒輪動力學(xué)的作用機制，進(jìn)一步探究粗糙齒面對系統(tǒng)動態(tài)特性的影響，從而為工程齒面精度設(shè)計提供參考，本文作者利用分形理論對粗糙齒面進(jìn)行分形表征，結(jié)合齒面摩擦因素，建立考慮粗糙齒面影響的齒輪多自由度非線性動力學(xué)模型，研究齒面粗糙度、齒面摩擦及工況對系統(tǒng)動力學(xué)特性的影響。

1 粗糙表面的分形表征

在齒輪的加工制造中，由于存在加工方法不同及刀具顫振等原因，實際加工齒面在微觀上都是凹凸不平的，即存在一定的表面粗糙度。表1所示為不同加工方法下的齒面粗糙度范圍，研究粗糙齒面對齒輪動力學(xué)特性的影響具有重要的實際意義。分形理論源自對海岸線形狀的研究，它是解決非線性幾何問題的常見方法。現(xiàn)實生活中，海岸線和粗糙表面輪廓線都是典型的分形曲線，粗糙表面的分形表征是分形理論在工程機械中的重要應(yīng)用，因此文中采用分形理論模擬隨機粗糙齒面。

表1 不同加工方法下的齒面粗糙度

目前，分形理論表征粗糙表面的方法主要有W-M函數(shù)模擬法、分形插值模擬法和時間序列模擬法等。W-M函數(shù)是處處連續(xù)而處處不可導(dǎo)且具有自仿射特征的分形曲線，在實際工程和科學(xué)研究領(lǐng)域中均得到了廣泛應(yīng)用。W-M函數(shù)構(gòu)造式為

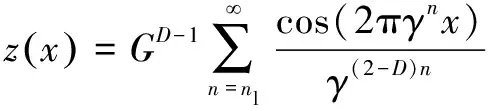
(1)

式中:為粗糙表面輪廓高度；為自仿射分形維數(shù)，它描述函數(shù)在所有尺度上的不規(guī)則性，對于二維分形，1<<2；為特征尺度系數(shù)，它決定粗糙輪廓的具體高度；為大于1的常數(shù)，一般認(rèn)為齒面波紋度、粗糙度近似滿足正態(tài)分布，故取1.5；為表面輪廓的截斷頻率;為最低截斷頻率。

輪廓算術(shù)平均偏差是最早被提出來的粗糙度評定參數(shù)，目前在國際上仍被多數(shù)國家采用。葛世榮、陳奇等人基于實驗測定，分別給出了粗糙度關(guān)于分形維數(shù)和特征尺度系數(shù)的推薦關(guān)系式：

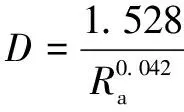
(2)

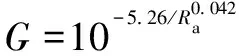
(3)

由此即可通過二維W-M分形函數(shù)生成不同表面粗糙度下的輪廓高度。圖1所示為分別為0.4、1.6和6.3 μm時粗糙表面的模擬結(jié)果。

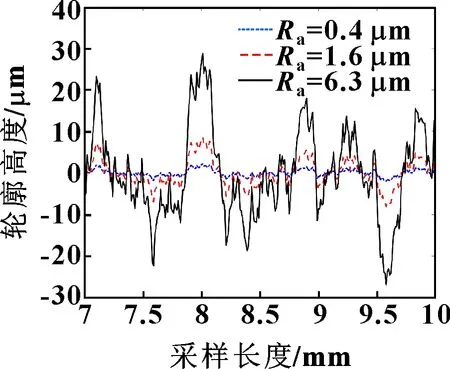
圖1 不同表面粗糙度下的輪廓高度

2 齒輪動力學(xué)建模

2.1 直齒輪副嚙合傳動過程

圖2所示為一對直齒輪副的嚙合傳動過程，由于直齒輪傳動的重合度一般在1～2之間，故存在單雙齒交替嚙合情況。主動輪受驅(qū)動扭矩的作用以角速度帶動從動輪旋轉(zhuǎn)，從動輪的角速度及所受扭矩分別為和。圖中為理論嚙合線，為實際嚙合線。齒對1在點嚙入時齒對2在單齒嚙合區(qū)下界點處嚙合，隨著齒輪轉(zhuǎn)動，齒對2在點退出嚙合，此時齒對1剛好到達(dá)單齒嚙合區(qū)上界點，然后經(jīng)過節(jié)點直至點，同時新一對的輪齒又從點嚙入。在雙齒嚙合區(qū)，主動輪受一對動態(tài)嚙合力、(LOA方向)和摩擦力、(OLOA方向)作用，和分別為齒對1和齒對2的摩擦力臂。

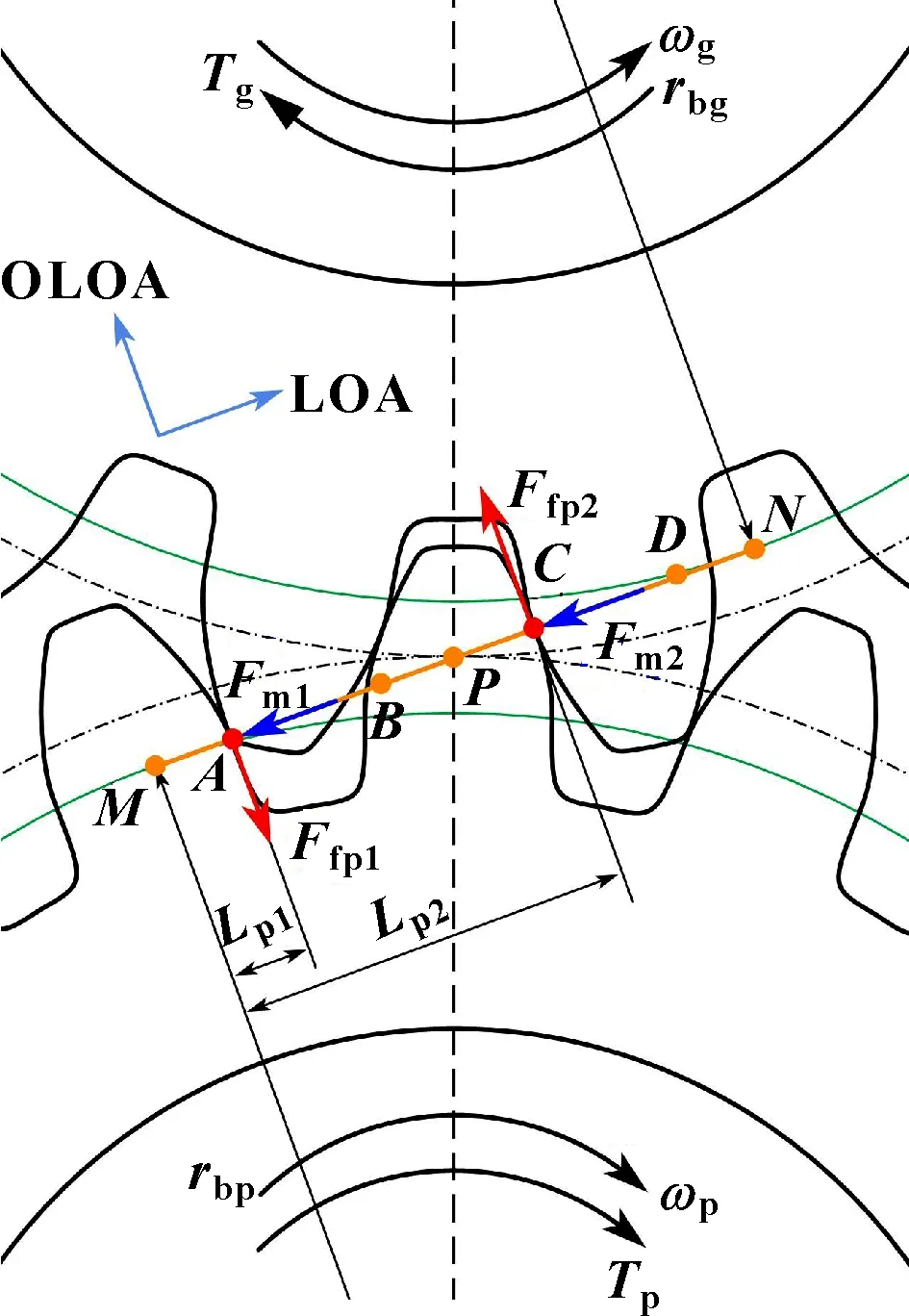
圖2 直齒輪副嚙合過程

2.2 動力學(xué)模型

利用集中參數(shù)法，建立如圖3所示的齒輪動力學(xué)模型。以圖示方向建立笛卡爾坐標(biāo)系，每個齒輪均有和方向的平移自由度及繞軸旋轉(zhuǎn)的扭轉(zhuǎn)自由度。圖中、分別為等效支撐剛度和支撐阻尼；、分別為嚙合剛度和嚙合阻尼；為靜態(tài)傳遞誤差；、、、分別為主從動輪的質(zhì)量與轉(zhuǎn)動慣量。為簡化研究，假定主、從動輪的等效支撐剛度和阻尼均相同。由于滑動摩擦較滾動摩擦大很多，僅考慮齒間滑動摩擦。由于側(cè)隙多在空載和輕載工況下影響較大，且側(cè)隙引起的輪齒脫嚙會導(dǎo)致齒面不存在摩擦作用，不考慮側(cè)隙影響。

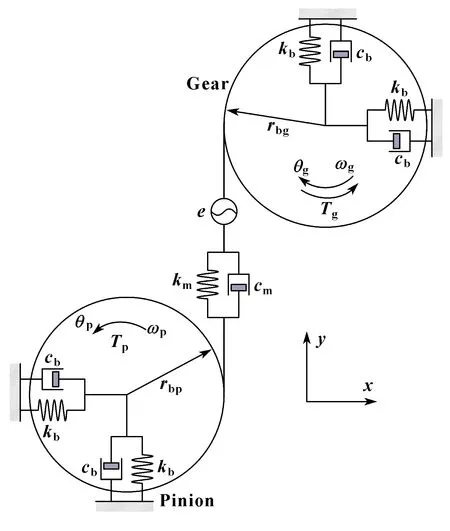
圖3 動力學(xué)模型

鑒于粗糙表面接觸的復(fù)雜性，假設(shè)兩齒面接觸時一齒面為粗糙表面而另一齒面光滑，且不考慮其他誤差因素影響，僅以粗糙輪廓高度作為靜態(tài)傳遞誤差，以此研究粗糙齒面對齒輪動力學(xué)特性影響。

定義主、從動輪沿嚙合線上的相對位移為動態(tài)傳遞誤差與靜態(tài)傳遞誤差的差值：

=-=-+--

(4)

作用在第(=1,2)對輪齒的動態(tài)嚙合力可表示為彈性嚙合力與黏性嚙合力之和：

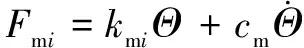
(5)

式中：m為第對輪齒的嚙合剛度，文中采用應(yīng)用十分廣泛的石川公式求解嚙合剛度，詳細(xì)公式此處不再贅述，嚙合剛度計算結(jié)果如圖4所示；為嚙合阻尼，可由如下經(jīng)驗公式表示：

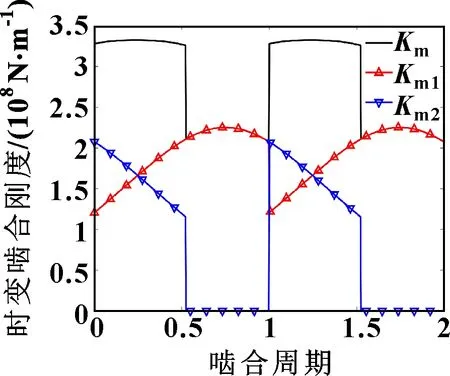
圖4 時變嚙合剛度

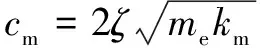
(6)

其中：為嚙合阻尼比；為齒輪副的等效質(zhì)量；為平均嚙合剛度。

定義為第對齒輪時刻在嚙合線上的位移：

=mod(,)+(-1)

(7)

依據(jù)齒輪嚙合幾何原理，第對輪齒上的摩擦力臂可由下式求得：

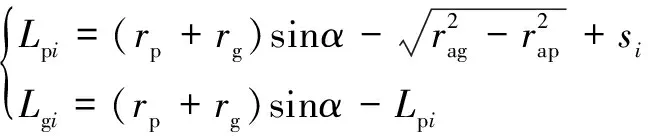
(8)

式中：、和、分別為主從動輪的節(jié)圓半徑和齒頂圓半徑。

主、從動輪第對輪齒所受的摩擦力分別為

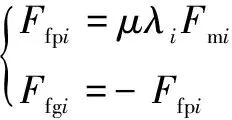
(9)

式中：為摩擦因數(shù)；為摩擦力換向系數(shù)，當(dāng)相對滑動速度為正時取“+1”，為負(fù)時取“-1”，在節(jié)點處為“0”，可借助符號函數(shù)將其表示為

=sign(g-p)

(10)

則摩擦力矩可表示為

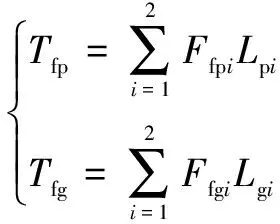
(11)

根據(jù)牛頓第二定律，系統(tǒng)的動力學(xué)微分方程為

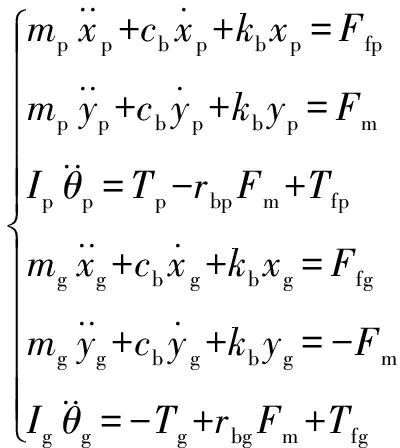
(12)

3 粗糙度對齒輪動力學(xué)特性的影響

齒輪傳動系統(tǒng)是極其復(fù)雜的非線性時變系統(tǒng)，其動力學(xué)方程一般難以獲得解析解，因此數(shù)值仿真是分析齒輪動力學(xué)問題的常用方法。此節(jié)選取一組齒輪基本參數(shù)，如表2所示，利用Simulink仿真器和內(nèi)置的定步長Runge-Kutta法對動力學(xué)方程進(jìn)行數(shù)值求解，研究相關(guān)參數(shù)對動力學(xué)特性的影響。

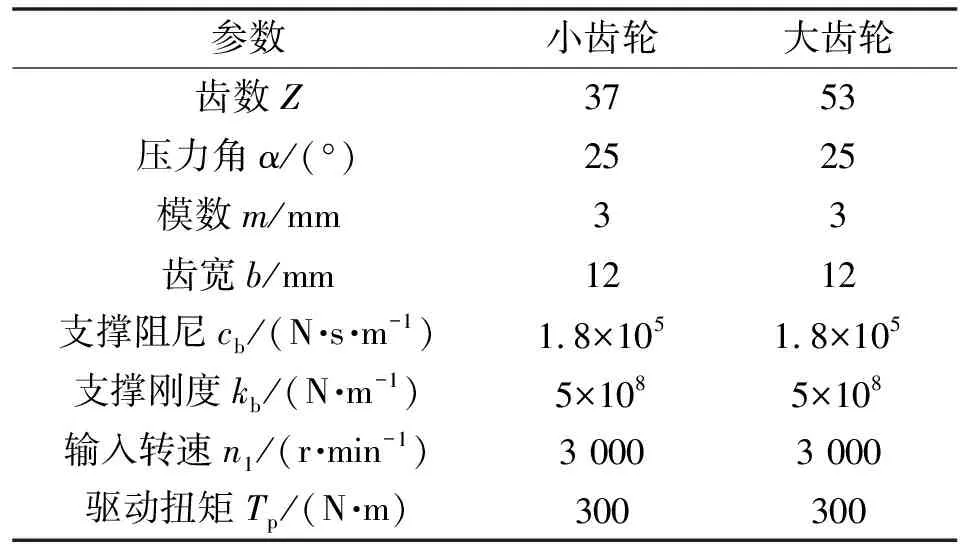
表2 齒輪基本參數(shù)

3.1 齒面粗糙度對動力學(xué)特性的影響

齒輪傳動過程產(chǎn)生的動態(tài)傳遞誤差是反映系統(tǒng)振動特性的關(guān)鍵因素，圖5為粗糙度分別為0.4、1.6、6.3 μm時動態(tài)傳遞誤差的時域譜、頻域譜和相圖。由圖5(a)可知：嚙合輪齒存在明顯周期性沖擊，當(dāng)粗糙度由0.4 μm上升至6.3 μm時，動態(tài)傳遞誤差顯著增大，經(jīng)計算其方均根值由23.49 μm上升至24.63 μm；由圖5(b)可知：頻率成分主要為嚙合頻率及其倍頻，粗糙度主要影響動態(tài)傳遞誤差的二階振動分量，對其他頻段影響較小；由圖5(c)可知：相圖為一不規(guī)則封閉曲線，表明系統(tǒng)為單周期非簡諧振動且隨著粗糙度上升，系統(tǒng)的周期運動更加復(fù)雜，振動愈發(fā)不穩(wěn)定，動態(tài)性能逐步惡化。

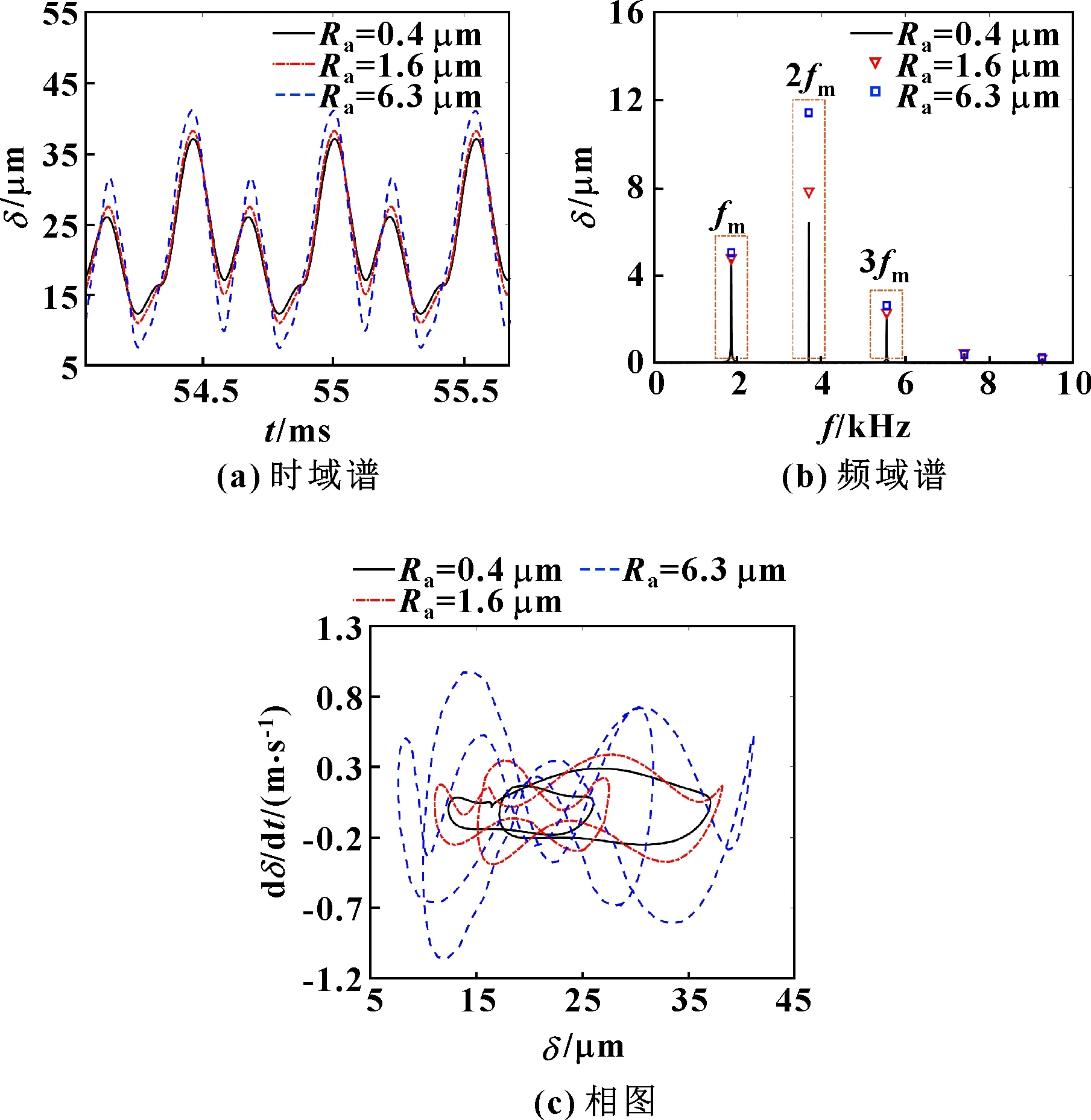
圖5 不同粗糙度下動態(tài)傳遞誤差

3.2 齒面摩擦對動力學(xué)特性的影響

當(dāng)齒輪傳動處于不同的潤滑狀態(tài)或齒面出現(xiàn)損傷時，齒面摩擦因數(shù)變化較大，目前仍無可準(zhǔn)確描述粗糙度與摩擦因數(shù)關(guān)系的解析式。此節(jié)以摩擦因數(shù)為0、0.05、0.2來表示不考慮摩擦、正常潤滑及損傷乏油工況，齒面摩擦對系統(tǒng)動力學(xué)特性的影響。圖6—圖8分別為小齒輪沿和方向的振動位移以及齒輪副動態(tài)傳遞誤差的時頻域響應(yīng)。

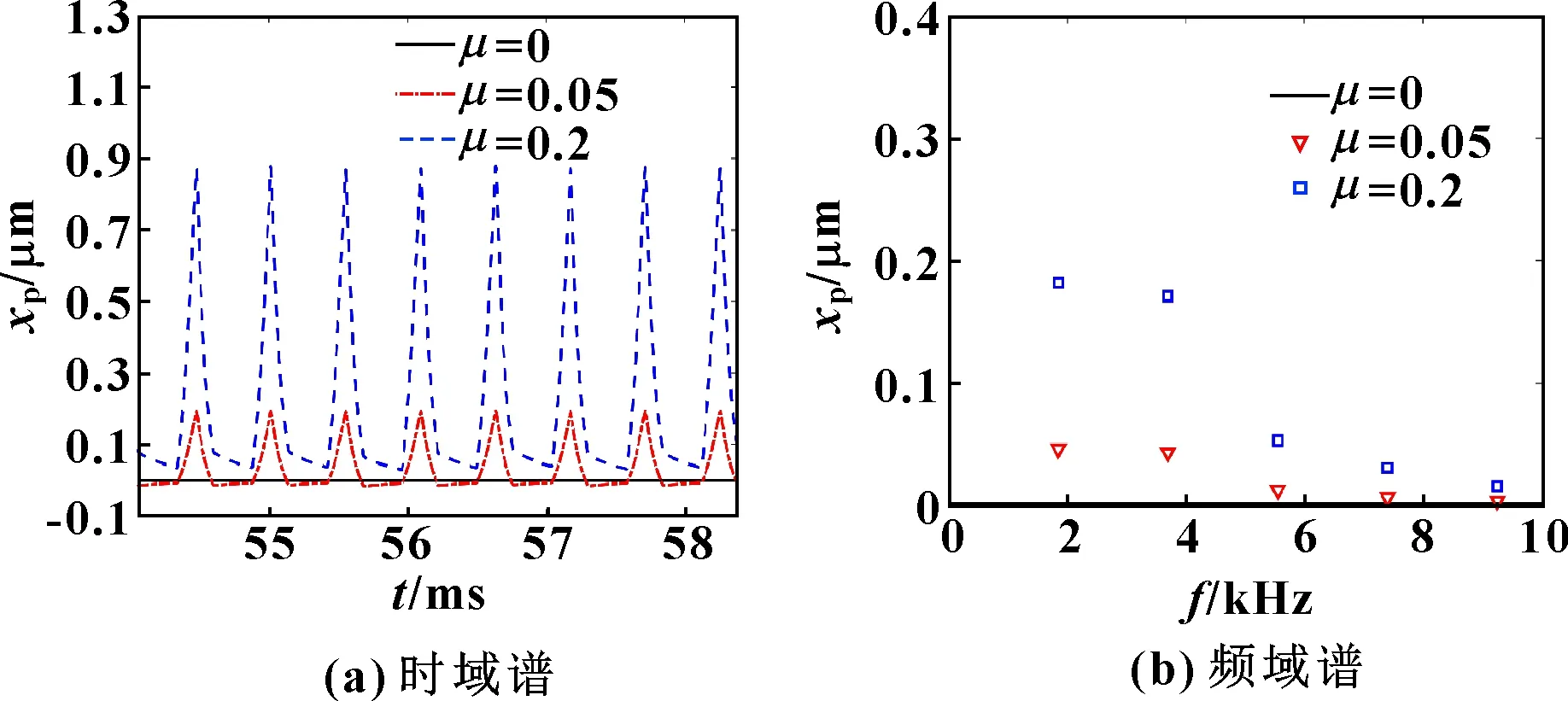
圖6 小齒輪x向振動位移

圖7 小齒輪y向振動位移

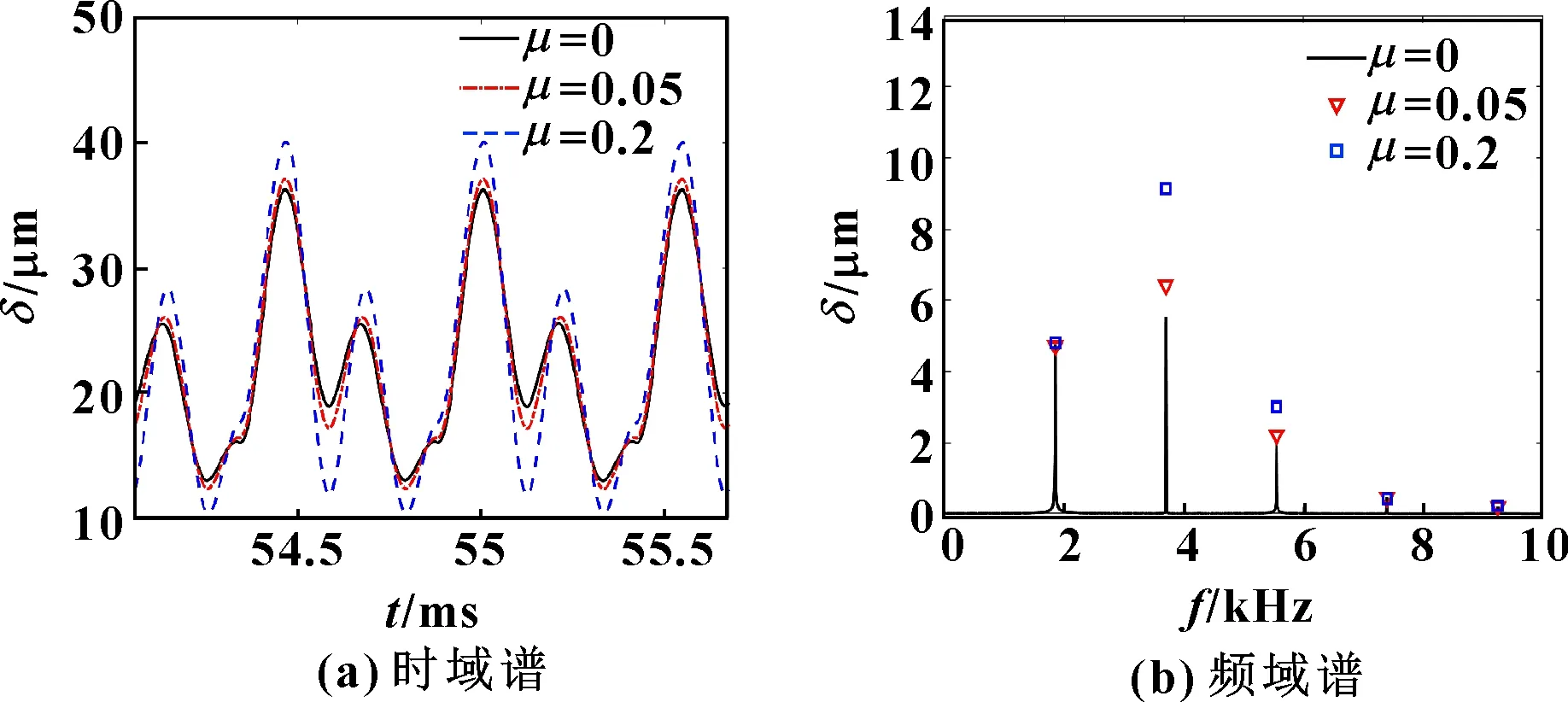
圖8 不同摩擦因數(shù)下動態(tài)傳遞誤差

由圖6—圖8可知：摩擦因數(shù)上升使得小齒輪沿和方向的振動位移以及系統(tǒng)的動態(tài)傳遞誤差均增大，表明齒面摩擦?xí)?dǎo)致系統(tǒng)的振動和噪聲加劇，這與文獻(xiàn)[15]的結(jié)論一致。此外，由于齒面摩擦作用于垂直嚙合線方向，它是導(dǎo)致方向振動的主要激勵，因而對該方向的振動影響更顯著。由圖6—圖8所示的頻域譜可知：齒面摩擦主要影響系統(tǒng)振動位移的前3階振動分量，對高頻振動分量的影響較小。

3.3 工況對動力學(xué)特性的影響

在實際應(yīng)用中，齒輪傳動機構(gòu)常工作于不同工況下，且現(xiàn)代工業(yè)正朝著高速、重載的方向發(fā)展，研究變工況下粗糙度對齒輪動力學(xué)特性的影響，對齒輪傳動系統(tǒng)的設(shè)計及應(yīng)用均具有重要意義。圖9所示為低速輕載、高速輕載和高速重載3種工況下粗糙度為0.4、1.6、6.3 μm時系統(tǒng)的動態(tài)傳遞誤差響應(yīng)，對應(yīng)的各工況參數(shù)如表3所示。

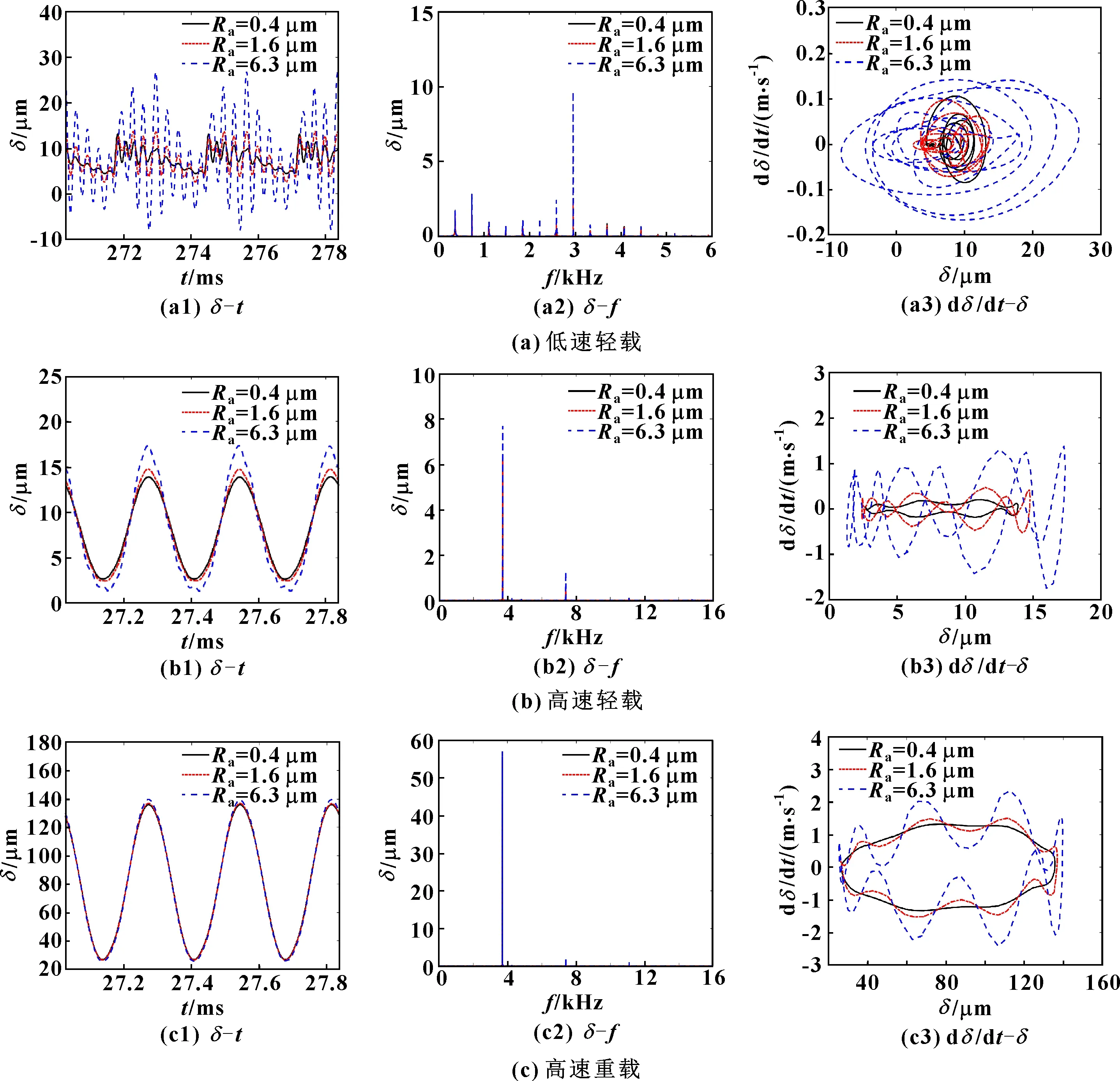
圖9 不同工況下動態(tài)傳遞誤差

表3 工況參數(shù)

由圖9可以看出：在低速輕載工況下，動態(tài)傳遞誤差的振動規(guī)律、頻率成分和相軌跡較為復(fù)雜，粗糙度上升后，動態(tài)傳遞誤差顯著增大，相軌跡愈發(fā)復(fù)雜，系統(tǒng)的振動特性逐漸變差；隨著工況由低速輕載向高速重載變化，動態(tài)傳遞誤差的沖擊明顯降低，頻率成分逐漸減少，相軌跡愈發(fā)趨于規(guī)則封閉曲線，系統(tǒng)的振動穩(wěn)定性提高；在高速重載工況下，粗糙度增大對系統(tǒng)動態(tài)傳遞誤差的時頻域響應(yīng)及相圖的影響較低速輕載時顯著減小。這表明當(dāng)轉(zhuǎn)速和扭矩增大時，齒輪傳動的嚙合時間減小，法向載荷增大，使得齒輪副的接觸周期與狀態(tài)發(fā)生明顯變化，進(jìn)而導(dǎo)致粗糙度對動態(tài)特性的影響越來越小。上述研究表明，粗糙度對齒輪動力學(xué)特性的影響因工況變化而不同，結(jié)合工況合理地進(jìn)行齒面精度設(shè)計，有利于進(jìn)一步平衡加工成本與傳動質(zhì)量之間的關(guān)系，降低齒輪傳動的振動和噪聲。

4 結(jié)論

本文作者從隨機粗糙表面對齒面誤差的影響入手，通過二維W-M分形函數(shù)對粗糙表面進(jìn)行了分形表征，建立了計及粗糙齒面和摩擦的齒輪非線性動力學(xué)模型。采用數(shù)值仿真方法研究了齒面粗糙度、齒面摩擦及工況對齒輪傳動系統(tǒng)動力學(xué)特性的影響。主要結(jié)論如下：

(1)粗糙度增大時，齒輪副的動態(tài)傳遞誤差增大，系統(tǒng)的周期運動更加復(fù)雜，振動穩(wěn)定性下降，動態(tài)性能逐步惡化；

(2)摩擦因數(shù)增大時，系統(tǒng)的動態(tài)傳遞誤差和振動位移均增大，齒面摩擦加劇了系統(tǒng)的振動和噪聲，且摩擦對垂直于嚙合線方向的振動位移影響較其他方向更明顯；

(3)粗糙度對齒輪動力學(xué)特性的影響因工況變化而不同，低速輕載工況下粗糙度對動態(tài)響應(yīng)的影響較大，隨著轉(zhuǎn)速和扭矩增大，粗糙度對動態(tài)響應(yīng)的影響愈發(fā)不明顯。結(jié)合工況合理地進(jìn)行齒面精度設(shè)計，有利于進(jìn)一步平衡加工成本與傳動質(zhì)量之間的問題。