信德文化中心HALL-B框架柱計算長度系數分析

陳志鋼

(上海天華建筑設計有限公司，上海 200235)

1 工程概況

前灘信德文化中心項目位于上海市浦東新區前灘地區，基地南至高青西路、北至海洋西路。地塊項目為辦公、酒店和文化演藝中心綜合體，項目占地面積約26 707 m2，總建筑面積約21.3萬m2。

其中HALL-B塔樓為本項目文化演藝功能的重要組成部分，地上5層，地下3層，建筑高度32.9 m，地上1層～5層層高分別為6.5 m，5.4 m，6 m，6 m，9.1 m; 結構體系采用鋼框架結構，樓板采用鋼筋桁架樓承板。

2 結構特點

根據建筑功能需求(如圖1所示),2層結構平面(如圖1(a)所示)東側和南側部分樓板挑空，形成1層～2層穿層柱，為避讓首層車道，部分穿層柱為斜柱，斜率不大于1∶6；4層平面圖(如圖1(c)所示)較大區域樓板挑空并抽柱，形成51.6 m×28 m開敞空間，開敞空間上方(如圖1(d)所示)采用鋼桁架。

GB 50017—2017鋼結構設計標準[1]第8.3.1條框架柱計算長度系數的基本假定為：

1)材料是線彈性的；2)框架只承受作用在節點上的豎向荷載；3)框架中的所有柱子同時喪失穩定性，即各柱同時達到其臨界荷載；4)當柱子開始失穩時，相交于同一節點的橫梁對柱子提供的約束彎矩，按柱子的線剛度值比分配給柱子；5)在無側移失穩時，橫梁兩端的轉角大小相等方向相反；在有側移失穩時，橫梁兩端的轉角不但大小相等且方向亦相同。 HALL-B塔樓各框柱受力狀態差異很大，難以滿足第3)條假定的要求，應進行穩定性分析。本文將從地下室對框柱計算長度系數的影響和穿層柱對框柱計算長度系數的影響兩方面進行分析。

3 地下室對首層柱計算長度系數的影響

有地下室的建筑一般采用含地下室的模型進行設計，本項目首層和2層層高較大且存在較多穿層柱，穿層柱高度約11.9 m，其長細比為控制尺寸的關鍵因素。而設計中發現采用規范算法計算框架柱長度系數時，有、無地下室對計算結果有較大影響。經分析，筆者認為地下室框架柱尺寸為地上鋼柱四周增加200 mm厚混凝土形成的型鋼混凝土柱，其承載力較首層鋼柱增加較多，不會與首層鋼柱同時喪失穩定性，不符合《鋼結構設計標準》中的第3)條假定。地下室框柱和首層混凝土梁的抗彎剛度之和遠大于首層鋼柱的抗彎剛度，其對首層框柱的轉動有較強約束，周邊地庫對塔樓在水平向平動亦有可靠約束，故首層柱底應接近于嵌固。為驗證分析結果，建立一個4×4跨的簡易模型進行對比分析，對比模型共4個,分別為：1)地下室模型規范算法；2)地下室模型整體穩定性分析方法，采用歐拉公式反算框架柱計算長度系數；3)無地下室模型規范算法；4)無地下室模型整體穩定性分析方法，采用歐拉公式反算框架柱計算長度系數。

模型參數：地上4層4×4跨，柱網尺寸8 m×8 m，鋼柱截面400 mm×400 mm×16 mm×16 mm，鋼梁截面550 mm×250 mm×12 mm×20 mm，樓板厚度180 mm，恒載2 kPa，不考慮活載，材料強度Q345B，層高4.5 m。

地下1層6×6跨，柱網尺寸8 m×8 m，混凝土柱截面900 mm×900 mm，混凝土梁截面400 mm×700 mm，樓板厚度180 mm，恒載2 kPa，不考慮活載，材料強度C35，層高5.5 m。

計算模型和線彈性整體穩定分析如表1所示。

表1 框柱計算長度系數

地下室和無地下室計算模型及第一階屈曲模態見圖2。

由圖2(b)和圖2(d)對比可知，第一階屈曲模態一致，整體失穩時地下室無變形，首層柱根部接近于嵌固；表1中有、無地下室模型采用整體穩定分析方法獲得的框柱計算長度系數分別為1.04和1.03，兩者基本一致，表明地下室對首層柱的約束作用等效于無地下室模型，即柱底接近于完全嵌固。另外，地下室模型規范算法的框柱計算長度系數1.47明顯高于其余三種模型，而無地下室模型規范算法的框柱計算長度系數略大于整體穩定性分析，較為適宜。

4 穿層柱對計算長度系數取值的影響

HALL-B塔樓首層共有框架柱47根，其中穿層柱11根；三層共有框架柱36根，其中穿層柱(含單方向無框架梁約束)19根，穿層柱占比較大。因穿層柱均至少跨越兩層，與《鋼結構設計標準》中基本假定框架柱均為同層的情況不一致，本項目穿層柱所占比例較高，對整體穩定性有較大影響。陳紹蕃先生所著《鋼結構設計原理》[2]第2.4節所述，框架結構失穩應作為一個整體來考察，如圖3(a)所示的橫梁兩端鉸接的剛架，橫梁跨中作用豎向力P，桿A和桿B彈性模量分別為EI與2EI，桿A和桿B軸力均為P/2，當桿A達到懸臂桿臨界力(π2EI/(2h)2)時，桿B僅達到臨界力的50%，由于桿B的側向支撐作用，桿A不會喪失穩定且可以繼續承載，桿B也達到臨界力時剛架整體喪失穩定性，此時P為π2EI/(2h)2+π22EI/(2h)2，由此可反算桿A計算長度系數為1.632，小于懸臂構件的2.0，說明桿B的支撐減小了桿A的計算長度系數；桿B計算長度系數為2.309，大于懸臂構件的2.0，支撐作用增大了桿B的計算長度系數，如不考慮此作用使得桿B的設計偏于不安全。同理分析穿層柱的情況，圖3(b)為穿層柱框架，當穿層柱桿A達到臨界承載力時，依靠框架中桿B的支撐作用桿A不會喪失穩定性，當桿A和桿B均達到臨界荷載，框架整體失穩，故當穿層柱數量較多時，此相互作用影響較大，不可以忽略，故本項目HALL-B所有框架柱(穿層柱和普通框架柱)均應考慮結構之間的相互支撐作用，否則導致計算結果的不安全。文獻[3]也對框架內部之間的支撐作用有較為細致的分析。

沿用第2節的算例模型尺寸進行分析，增加穿層柱對其余框架柱的計算長度系數是否有影響。第2節算例二層樓面端跨取消部分樓板后形成穿層柱模型，如圖4所示。

圖4柱1～柱5計算長度系數對比如表2所示，其中柱3～柱5的周邊一跨結構布置沒有調整，如按照規范算法，其計算長度系數應保持不變；但整體穩定性分析結果顯示穿層柱模型中柱3～柱5的計算長度系數較原模型均有加大，說明其余框架柱對穿層柱有一定的支撐作用，此作用導致其余框架柱計算長度系數加大，此時采用規范算法可能不安全。

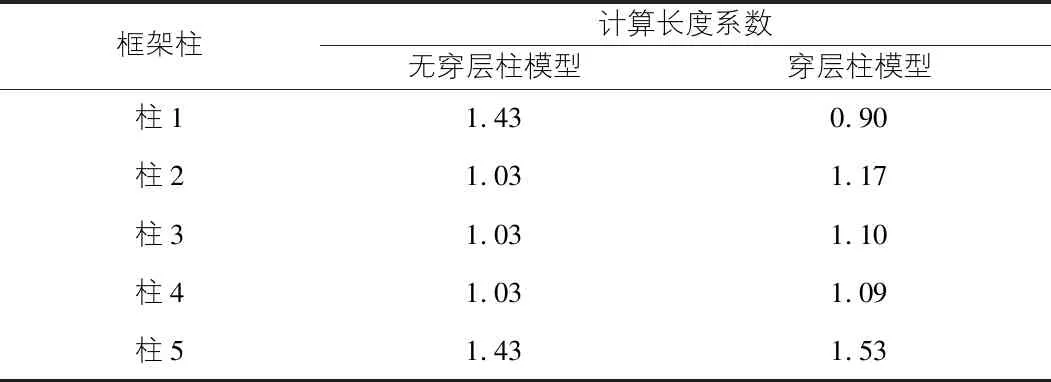
表2 計算長度系數對比表

穿層柱的計算長度系數一般可通過結構的整體穩定性分析獲得(見圖5(a))，也可僅在穿層柱柱頂加載進行的獨立柱的穩定性分析獲得(見圖5(b))。

對于本項目，兩種分析方法所得計算長度系數結果相差較大，文獻[4-5]均提及了兩種分析方法，但均未對其各自的適用范圍進行明確。整體穩定性分析能夠反映穿層柱周邊構件相互作用；獨立柱穩定性分析是對獨立柱進行的無側移工況下的穩定性分析，忽略了獨立柱與周邊結構的相互作用。

對于鋼框架結構，采用獨立柱穩定性分析方法時，默認周邊框架柱提供了可靠支撐防止獨立柱側移失穩，即穿層柱為圖3(b)中的桿A，其余框架柱為圖3(b)中的桿B，但是經過前面算例分析，此時普通柱(桿B)仍采用規范算法是偏于不安全的，其計算長度系數應進行調整，建議鋼框架結構宜采用整體穩定性分析方法，如穿層柱所占比例極小，也可考慮獨立柱穩定性分析方法。對于鋼框架-支撐(剪力墻)結構，支撐(剪力墻)為抗側剛度的主體，采用獨立柱穩定性分析時，其周邊支撐作用主要來自于剛度比較大的支撐(剪力墻)，獨立柱對支撐或剪力墻作用極小，可基本忽略，此時可采用單柱穩定性分析方法；當然如穿層柱及周邊相連框柱未與支撐(剪力墻)連接時，應對穿層柱及周邊相連框柱的局部范圍看作整體進行穩定性分析。本項目穿層柱比例非常大，采用線彈性整體穩定性分析方法，通過歐拉公式反算所有框柱的計算長度系數，且計算長度系數取值不小于1。

根據前述分析，穿層柱可通過普通框柱的支撐作用降低穿層柱的計算長度系數，在長細比滿足規范的前提下，計算長度系數的減小意味著可以使用更小的截面。

因穿層柱經常出現在入口大堂等建筑功能關鍵位置，建筑設計師希望柱截面盡量小，那么柱截面的最小限值是什么。如果將框架結構的穩定看作整體穩定，桿件的穩定可看做局部穩定，在整體結構中局部穩定不應先于主體結構失穩，且應具有一定的安全余量，即整體穩定性分析所得的長細比不得小于單柱穩定性分析的結果[6]。

5 結論

1)地下室具有較好的嵌固剛度時，地下室框柱不會與首層鋼柱同時失穩，首層鋼柱的計算長度系數取值時可不考慮地下室。

2)結構中有較多穿層柱時，應對穿層柱和普通框柱的計算長度系數進行專項分析，不能直接按《鋼結構設計標準》采用，直接按規范采用可能導致計算結果的不安全。

3)框架結構的穿層柱應采用整體穩定性分析獲得計算長度系數；框架-支撐(剪力墻)結構中穿層柱可采用單柱穩定性分析。

4)采用整體穩定性分析獲得計算長度系數不應小于單柱穩定性分析計算結果，且應留有一定的余量。