朱祖煌

(諸暨中學,浙江 諸暨 311800)

1 數學解題教學中的問題鏈設計

在數學教學中，“解題”教學是一種最基本的活動形式.無論是核心素養中數學抽象、邏輯推理的提升，還是通過數學運算促進和提升學生的數學思維，形成規范化分析和思考問題的品質，養成嚴謹求真務實的科學素養，都離不開問題鏈的精心設計[1].數學問題鏈教學不僅關注了學生基礎知識與基本技能的掌握，更關注了學生對數學知識理解的深度.在問題鏈教學中，教師常常通過問題組織學生的學習內容，用“鏈”去引導學生學會思考，在教師的預設問題和學生的生成問題中評估學生的知識掌握程度和知識拓展與遷移能力.筆者在日常解題教學中，結合導問式教學方式，以數學問題為載體，以主干問題—延伸問題—提煉問題為教學組織形式，以學生辨析、師生辯駁為教學手段，引導啟發學生主動思考、探討(如表1).在問題鏈的解決過程中進一步引導學生提問，從而培養學生的數學學習力(知識與經驗、思維與方法、批判與創新)，進而提升學生發現與解決問題的能力[2].

表1 基于提升學生數學學習力的數學解題教學原則與問題鏈的設計

2 以平面向量的解題項目化教學為例

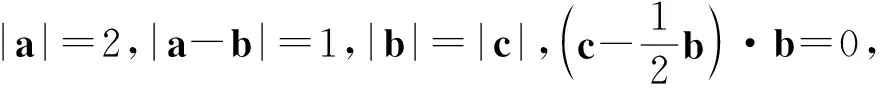
主干問題問題1～問題5.

問題1在起點問題中，描述幾何關系的量有哪些？

通過審題環節，理解題中向量模長與向量數量積等基礎知識點的數學含義.基于知識內容教學的主題思維設計如下問題鏈：

問題2-1題中的代數關系|a|=2,|a-b|=1,|b|=|c|，用幾何語言如何描述？

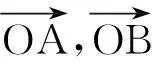
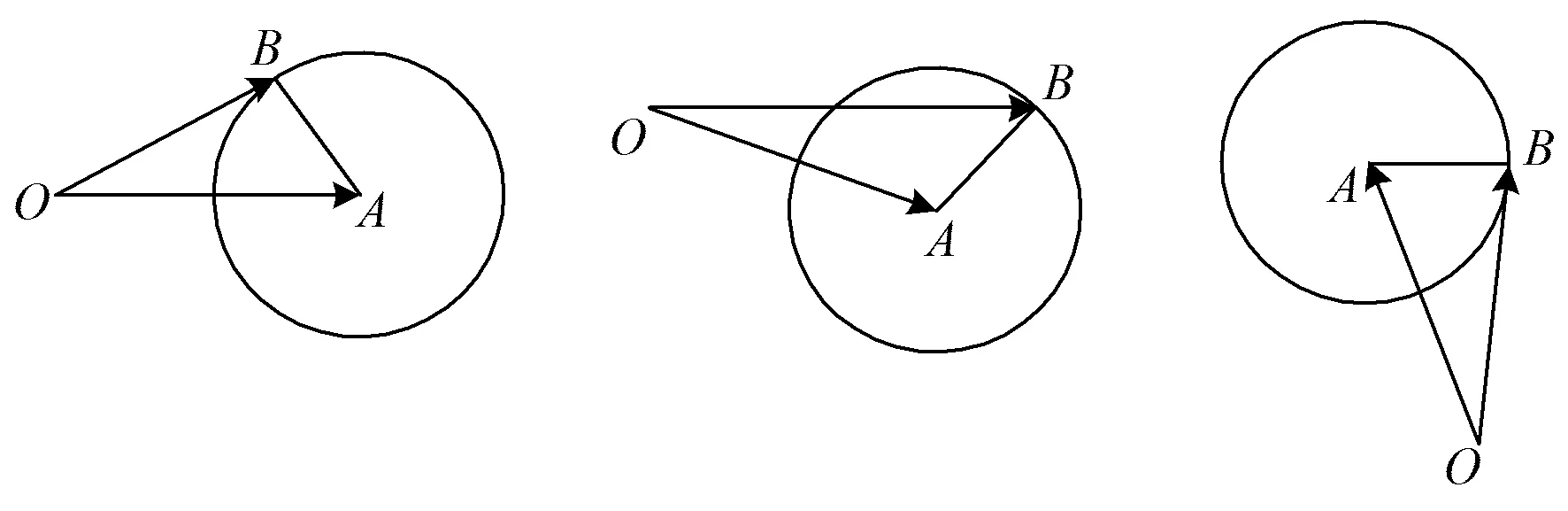
圖1 圖2 圖3

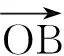
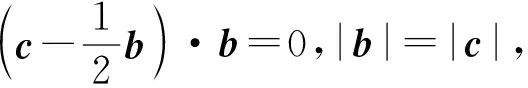
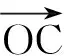
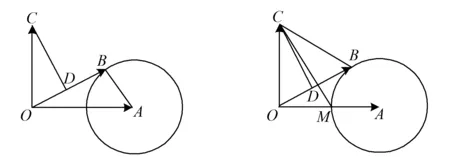
圖4 圖5

問題2-3(追問與辯駁)此時△OBC確定嗎？為什么？

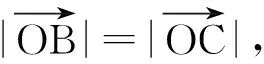
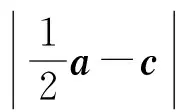
課堂預設表示點C到OA中點M的距離，即線段|CM|(如圖5).

問題3-1在圖6中，要求線段|CM|的最大值，其中不變的幾何量是什么？與|CM|的關系如何？

課堂預設點B在⊙A上運動，且|OC|=|OB|保持不變，故點C的運動是由點B的運動而變化的.點M是一個確定的點，因此需要確定動點C的軌跡.

課堂生成如圖6，|CM|≤|DM|+|CD|，且

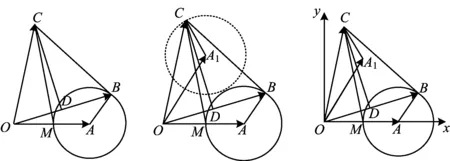
圖6 圖7 圖8

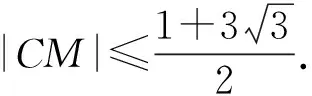
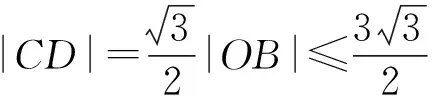
問題4-1能從幾何角度出發，確定動點C的軌跡嗎？

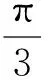
課堂生成動點B的軌跡是圓，動點C與動點B的運動相關，可以建立直角坐標系，利用求軌跡方程問題中相關點的思想確定動點C的軌跡方程，從而確定軌跡類型(如圖8).

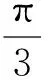
課堂預設利用復數的乘法的幾何意義可以表示點B,C之間的關系.設點C(x1,y1)對應的復數為z1=x1+y1i，點B(x0,y0)所對應的復數為z0=x0+y0i，則

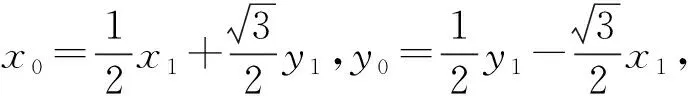
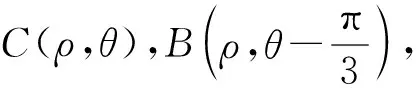
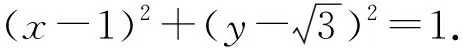
問題4-3(延伸問題1)描述動態幾何中，常見的變量有哪些？

課堂預設線段長度變量x，角度變量θ.

問題5-1(延伸問題2)這樣的解題策略關鍵點在哪里？

課堂預設在用向量法解決幾何問題中，借助幾何直觀，用幾何語言轉化為向量語言，畫出各個條件表征的幾何元素.

問題5-2(延伸問題2)如何計算幾何元素的最值？

課堂預設1)利用幾何觀，尋找幾何元素中的變與不變量，通過轉化求幾何最值；2)利用代數運算，將幾何問題轉化為代數問題，由數形結合思想構建幾何之間的橋梁.

問題6(提煉問題1)通過起點問題，你能總結解決此類向量問題的一般策略嗎？

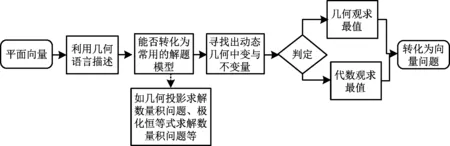
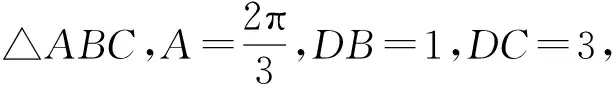
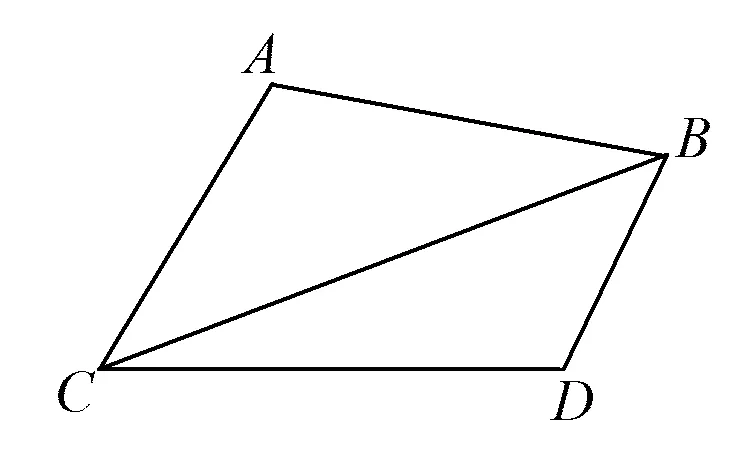
圖9

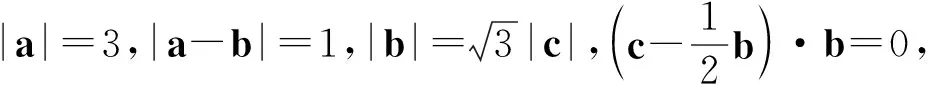
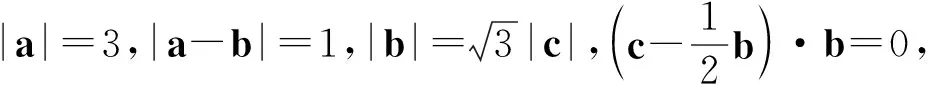
問題8(延伸問題4).

練習1已知向量a,b滿足|a|=1,=60°且c=-2a+tb(其中t∈R),則|c|+|c-a|的最小值______.

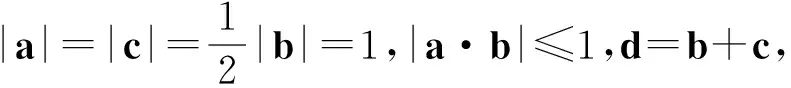
問題9(提煉問題2)以向量的共線問題為例，使向量語言與幾何語言實現相互切換.

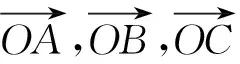
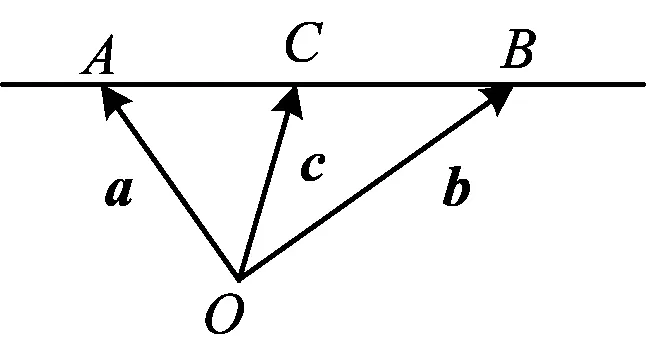
圖10

課堂預設平面向量中引入參數，激活了圖形的變化.在動態幾何中，恰當的“文式圖”的建構是圖形語言和向量條件間切換的“密碼”，從而實現了代數與幾何間的自由切換.

課堂生成以常見幾何元素的“文式圖”為例，以小組為單位，拓展思維，展開豐富的幾何元素與向量語言的轉換的拓展性作業，以思維導圖呈現.

課后練習請設計一張平面向量中常見向量語言與幾何語言問題清單.

3 結語

結構化是數學問題中的一個典型特征——數學對象之間存在著各式各樣的聯系.本文以平面向量的解題項目化教學為例，給出了基于提升學生數學學習力的解題教學原則與問題鏈的設計策略.課堂的主干問題鏈設計，立足基本知識，突出核心思想方法——向量代數與幾何的自由切換.表現在：一方面，通過課堂預設與課堂生成，將課堂在教師的導引下以學生為主體，強調在思考的脈絡中不斷延伸和拓展問題，以此激發學生探究數學知識的思維，提升數學學習力.另一方面，通過提煉問題，引導學生參與和歸納解題思想方法，給出思維導圖式的解題策略和文式圖表示的知識清單，真正落實核心素養下的解題教學目標.