汽車懸掛系統動力學建模與分析
甘華權,李海艷
(廣東工業大學機電工程學院,廣州 510006)
0 引言
隨著現代科學技術的不斷發展和生活水平的不斷提高,人們對汽車的功能需求越來越趨于多樣化和多元化。除了作為日常代步行駛之外,人們對汽車舒適性和平穩性的要求也越來越高。由于汽車懸掛系統綜合多種作用力,對車輛行駛的振動影響較大,進而汽車振動直接影響了汽車的穩定性、舒適性以及安全性,所以研究汽車懸掛系統的振動變形對改進汽車的穩定性、舒適性和安全性有著重大的意義[1]。
汽車懸掛系統屬于柔性多體系統的范疇[2],其在運動時會產生剛性與彈性變形的耦合運動[3]。所以汽車懸掛系統動力學建模需要考慮彈性變形,但是彈性變形有無限維自由度的特點,所以無法求得其精確解。目前比較常用的是通過有限單元法進行離散化處理進而求取其近似解[4]。例如,Patil等[5]利用有限元方法來求解柔性臂運動到特定位置情況下的撓度。許志華[6]使用有限元方法建立自卸車懸掛系統非線性有限元接觸模型。Nabawy等[7]使用平面桿單元建立了一種綜合的有限元模型來研究雙叉臂懸架系統的動態響應。然而為了方便模型求解,很多學者使用有限單元法對汽車懸掛系統動力學建模中一般會選擇簡化懸掛系統模型同時忽略一部分小變形,雖然減少了一些計算量,但也降低了一些動力學模型的精度,而且有限單元法的精度和網格單元劃分的大小相關,對于像汽車懸掛系統這樣的復雜系統,即使在簡化了模型的情況下,為了保證計算精度的網格單元會劃分的比較小,計算量也仍然比較大。
因此,本文以汽車懸掛系統為研究對象,提出了一種利用模態方法進行降維求解的方法,該方法首先通過拉格朗日方程法建立準確的汽車懸掛系統的非線性柔性多體動力學模型。然后對懸掛系統的彈性變形進行離散化處理,并通過有限階級數展開式精確表示該彈性變形。最后使用廣義α方法迭代求解該模型,并與有限單元法的柔性多體動力學建模求解結果進行對比分析,得出該方法應用于柔性多體動力學建模的優勢。
1 汽車懸掛系統動力學建模
1.1 建立參考坐標系
如圖1所示,1、3、5、7為車輪,2、4、6、8為柔性臂,9為車架,10~13為減震器。分析整車懸掛系統需要建立一系列的坐標系來表示其位置,其中oxyz為整體坐標系,然后以質量塊i(i=1,2,…,9)的重心oi為局部坐標系原點,建立與整體坐標系平行的初始狀態的局部坐標系oixiyizi。
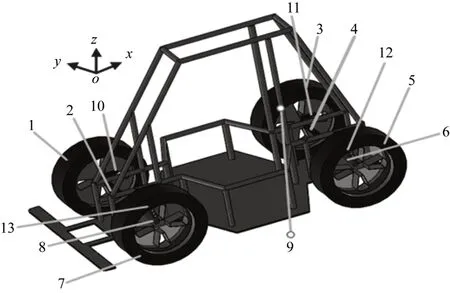
圖1 汽車懸掛系統
整車懸掛系統根據解耦控制方法,可以由4個1/4懸掛系統和一個為車架與受到的外力組成的系統組成。在整車懸掛系統中,所有的運動部件全部考慮為均質質量塊[8]。
如圖2所示,以1/4懸掛系統為例進行分析。首先,1為車輪,2為柔性臂,10為減震器,可替換為彈簧阻尼器,質量忽略不計。整體坐標系為oxyz,車輪1的局部坐標系為o1x1y1z1,柔性臂2的局部坐標系為o2x2y2z2(圖中未顯示的x、x1與x2軸為由紙面向里)。由于柔性臂2的長度遠大于其截面的直徑,柔性臂的截面方向的變形變化率非常小,所以將柔性臂簡化為空間梁結構。
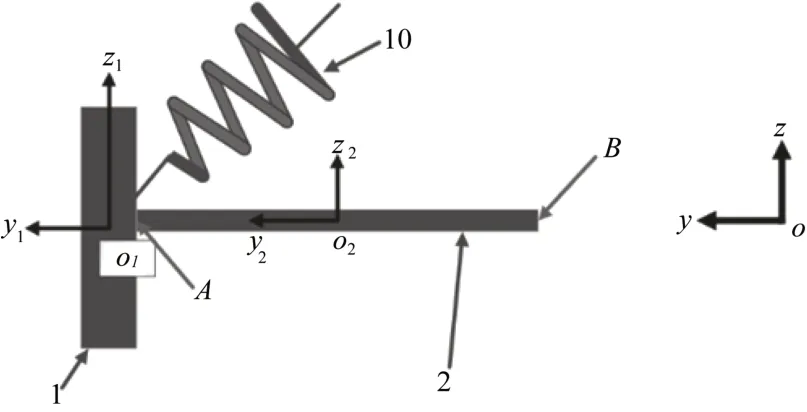
圖2 1/4懸掛系統示意圖
假設在簡化的空間梁2上存在某一點p,則該點p在局部坐標系o2x2y2z2上的位移矢量為:
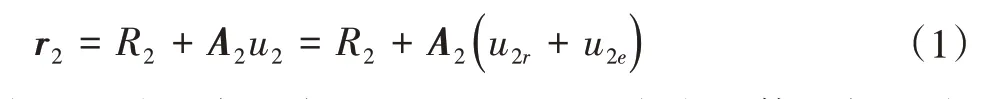
式中:R2為局部坐標系o1x1y1z1的原點在整體坐標系中的位置;A2為將柔性臂局部坐標系位移轉換到整體坐標系的旋轉矩陣;u2r和u2e分別為p點在局部坐標系o2x2y2z2上的剛性和彈性變形位移。
1.2 動力學模型建立
考慮到汽車懸掛系統動力學方程非常復雜,而使用拉格朗日方程法是直接建立外力與運動部件變量的關系,不涉及運動部件之間的各種約束力,原理相對簡單,所以本文利用拉格朗日方程法建立汽車懸掛系統的動力學模型。下面以1/4汽車懸掛系統為例,其拉格朗日方程為[9]:

式中:Qi為運動部件i廣義坐標的廣義外力;λ為拉格朗日乘子向量;Cqi為運動部件i的約束雅克比矩陣;qi為運動部件i的廣義坐標;Ti為運動部件i的動能。
Ti計算如下:

式中:q?i為qi對時間t的一階微分;Mi為運動部件i的質量矩陣。
根據式(3)、虛功原理以及邊界條件可求得1/4懸掛系統的動力學方程為:

式中:q?ii為qi對時間t的二階微分;Ki為運動部件i的剛度矩陣;Qvi為運動部件i二次速度矢量;Qci為運動部件i的約束雅克比矩陣余量。
其中,可根據以下式計算運動部件i二次速度矢量[10]:

進一步的,可以將式(4)寫成以下的矩陣形式:
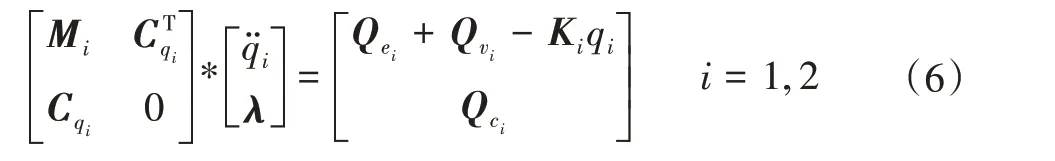
最后同理,可得整車懸掛系統動力學模型為:

2 動力學模型求解
2.1 動力學方程降維
由于拉格朗日方程法推導得到的汽車懸掛系統柔性多體動力學模型的方程是一組時變、非線性和強耦合的偏微分-積分方程,所以求汽車懸掛系統動力學模型的解析解非常困難。在這種情況下,一般是將無限維的動力學模型通過離散的方法進行降維,得到有限維的動力學模型。目前柔性多體動力學模型的常用的降維處理方法主要是有限單元法,該方法通過劃分單元的大小保證其求解精度。單元劃分越細時,離散后的動力學模型維度就越高,計算量就越大,計算效率就越低。而本文通過將彈性變形離散成基函數與對應時間系數乘積的級數展開式進而進行降維處理,將其代入前面求得的動力學模型即可得到降維后的低維近似模型。
首先根據柔性臂j的局部坐標系ojxjyjzj和柔性臂j的振型函數取特殊組合的三角函數為基函數:

式中:yj為柔性臂j在y軸上的位置表示;Lj為柔性臂j的長度,(i=1,2,…,N),ωi為柔性臂的固有頻率。
然后,將柔性臂j的彈性變形離散成式(8)的基函數與對應時間系數乘積的有限級數展開式表示:
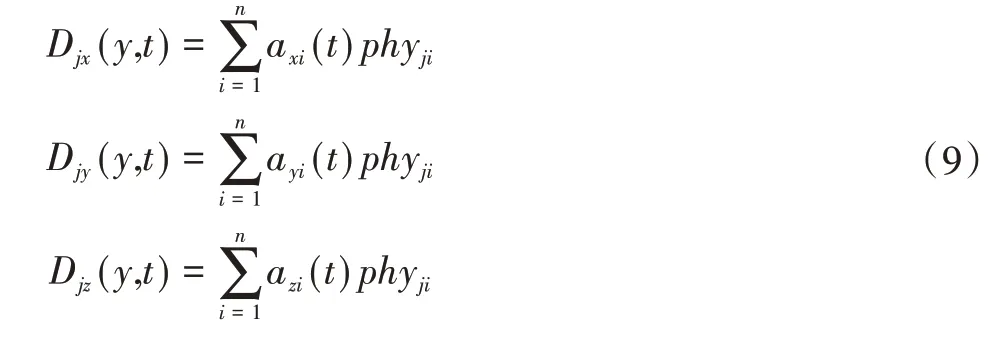
式中:axi(t)、ayi(t)、aji(t)為待求的與時間相關的權函數。
根據柔性臂兩端變形為零的邊界條件,可得:

進而計算求得參數dji為:
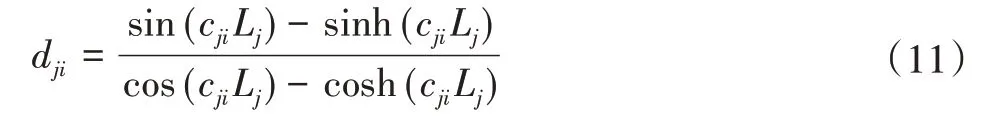
最后,本文取前2階級數展開式精確表示其柔性臂j的彈性變形:
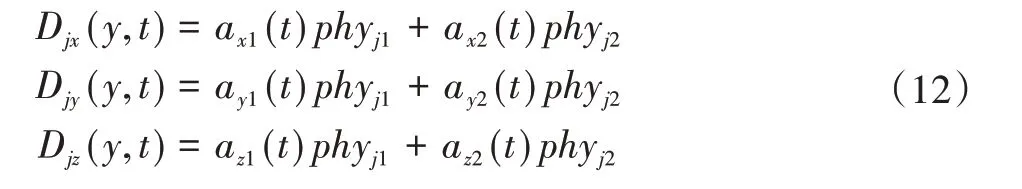
將上述離散的彈性變形代入前面求得的汽車懸掛系統柔性多體動力學模型中,得到降維后的低維柔性多體動力學模型。
根據上面彈性變形的表示形式可以得到以下剛度矩陣[11]:
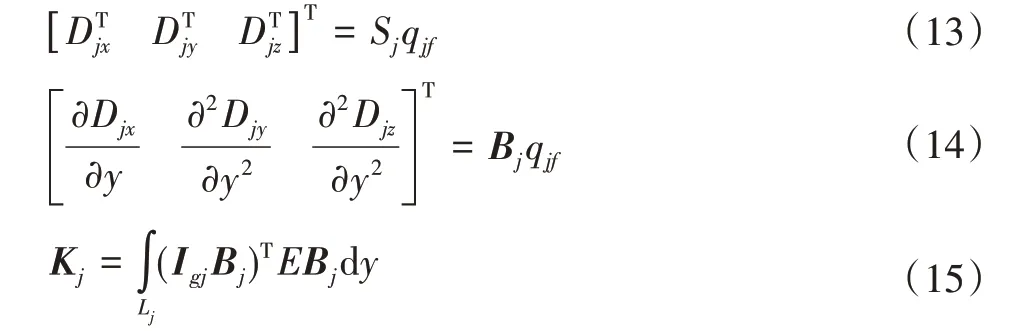
由上式可求得柔性臂j的形函數Sj、幾何矩陣Bj和剛度矩陣Kj,式中qjf為柔性臂j變形對應的廣義坐標,E為彈性模量。則有:

式中:Smj為質量塊j的截面面積;Igxj為質量塊j關于x方向的慣性矩;Igzj為質量塊j關于z方向的慣性矩。
2.2 動力學方程求解
如圖3所示,通過拉格朗日方程法可建立的汽車懸掛系統柔性多體動力學模型,通過求逆矩陣的方法求得初始加速度矢量和拉格朗日乘子。然后將初始時刻t0時刻的位移、速度、加速度等矢量作為廣義α方法[12]的初始迭代值,通過廣義α方法迭代求取t1時刻的相應位移、速度、加速度等,然后以t1時刻的相應位移、速度、加速度為作為t2時刻廣義α方法迭代的初始值求t2時刻的相應位移、速度、加速度等矢量。然后依次類推,依次求解,直到誤差小于預設誤差值且執行到未尾時刻tn則程序迭代結束,并輸出最后tn時刻相應的位移、速度、加速度矢量等。
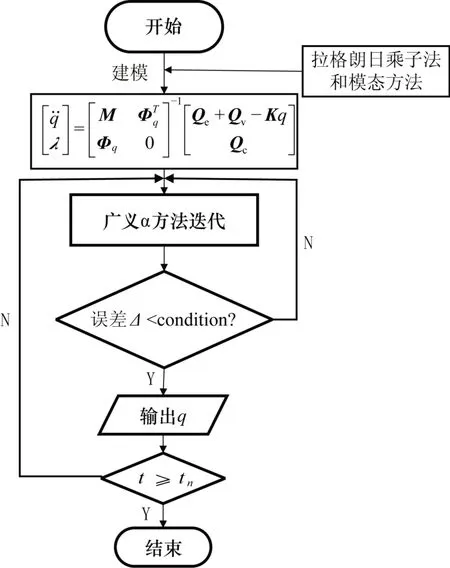
圖3 動力學模型求解流程
3 仿真與結果分析
通過具體參數進行數值仿真,車前端、后端的柔性臂長度分別為0.38 m、0.35 m,車輪、車架質量分別為20 kg、300 kg,彈性模量為200 GPa,密度為7800 kg/m3,彈簧彈性系數為10000 N/m,車架質心( 0.25,0,0.36)m,柔性臂截面內、外圓半徑分別為0.015 m,0.01 m。
圖4所示為沿x軸方向的彈性位移的比較,實線為本文方法求解得到的x軸彈性位移,虛線為有限元方法求解得到的x軸彈性模型,第一到第四行分別為柔性臂2、4、6、8的x軸彈性位移對比。

圖4 不同時刻柔性臂x軸變形位移
圖5所示為柔性臂中點沿z軸方向的彈性位移的比較,其中實線為本文方法表示的動力學模型求解得到的z軸彈性位移,虛線為有限元方法表示的動力學模型求解得到的z軸彈性模型,圖5(a)~(d)分別為柔性臂2、4、6、8的z軸彈性位移對比。

圖5 不同柔性臂中間節點變形位移
從圖4、圖5可知:首先,將彈性變形降維到64維的動力學建模求解的有限元方法與將彈性變形降維為二維的動力學模型求解的本文方法計算得到的不同時刻柔性臂x軸變形位移及不同柔性臂中間節點變形位移趨勢一致,且結果相差無幾,即精度相當;其次,本文方法求解所用時間僅為0.79 s,而有限元方法求解所用時間為2.3 s,其所用時間是本文方法的4倍多,即本文方法的計算效率遠高于有限單元方法;最后,如果進一步提升求解動力學模型的精度,有限單元法的網格劃分將會更多,計算量將大大增大,而本文則是只需增加一兩階基函數即可,所以在相同精度下,本文方法在求解效率方面優勢非常顯著。
4 結束語
本文通過以整車汽車懸掛系統作為研究對象,考慮彈性變形對汽車懸掛系統的影響,將柔性臂簡化成柔性空間梁結構,不忽略柔性臂的軸向和截面變形,使建立的汽車懸掛系統的柔性多體動力學模型比以往的將柔性臂簡化成平面梁表示動力學模型更完整。通過對比整車汽車懸掛系統動力學模型有限單元法降維求解和本文所提方法可得,兩種方法都可以保證整車汽車懸掛系統動力學建模的精度,在求解精度相差不大的情況下,本文所提方法的計算效率明顯要高得多。
為了進一步研究汽車懸掛系統運動中產生的彈性變形對汽車懸掛系統振動的影響,以后的研究通過建立更高維的柔性多體動力學模型和研究其振動頻率進行分析。

