基于CNN-BiGRU的水電機組振動趨勢預測

鄧玉敏，張雪桂，馬 歷，嚴耀亮，李超順

（1.中國長江三峽集團有限公司，武漢 430000；2.華中科技大學土木與水利工程學院，武漢 430074）

0 引 言

水電機組作為水力發電的關鍵設備，機組的安全穩定運行至關重要，其運行狀態信息通常表征在機組的一系列監測物理量中。因此可以通過采集到的監測數據進行分析，并通過預測模型對設備在未來某一時期狀態趨勢進行預測［1］。

水電機組的狀態信息蘊藏于振動信號中。在工程實際中，振動擺度信號蘊含了約80%的機組性能狀態信息，通過分析振動信號可以獲取機組的健康狀態［2，3］。水電機組振動趨勢預測是一個非線性非平穩的序列預測問題［4］，針對狀態趨勢的預測，例如，文獻［5］通過對機組水導軸承X 方向建立了BP 神經網絡預測模型進行預測，但此方法需要大量長時間的機組振動數據做基礎；文獻［6］通過支持向量回歸機（SVR）的預測模型完成對上機架振動、水導擺度歷史數據進行趨勢預測，但此方法容易出現“過學習”現象；文獻［7］采用時間序列模型預測法中的自回歸滑動平均（ARMA）模型，分別預測抽水和發電工況下的機組上導軸承和上機架的振動趨勢，證明了時間序列預測法可實現不同機械設備的振動趨勢的預測；文獻［8］針對水電機組信號的復雜非平穩特性，提出了一種基于能量熵重構（EER）與支持向量回歸（SVR）的混合預測模型，通過對信號的重構從而降低復雜度，最后得到最優SVR，提高了預測模型精度；文獻［9］使用神經網絡和支持向量機的預測方法，雖取得較好的效果，但對于水電機組這種非常復雜的系統進行神經網絡訓練時，因其系統復雜規模龐大，神經網絡模型的學習訓練需要較長的時間，降低了神經網絡的實用性。

文獻［10］采用WTD方法對振動信號數據進行降噪處理，再采用BiGRU 網絡建立振動信號預測模型，完成振動信號的趨勢預測；文獻［11］針對水電機組的振動信號的非平穩性、非線性的特點，提出了基于VMD 的CNN-LSTM 混合神經網絡的趨勢預測方法，與傳統神經網絡相比，CNN 可以更好地提取數據內在特征，構建網絡時所需參數更少，在保證精度的同時提高了計算速度。

為了進一步提高水電機組振動預測精度，針對目前單一模型難以獲得最優預測結果的問題，提出了一種CNN-BiGRU 模型組合的水電機組振動預測方法，并構造出CNN-BiGRU 網絡組合預測模型。利用CNN 提取數據局部特征，實現了對數據潛在特征關系的挖掘。又因水電機組振動信號在時間序列中存在聯系，為完成時序信號的特征挖掘預測，故將CNN 網絡和BiGRU 網絡進行并行預測，通過多模型組合預測來避免單一模型難以獲得最優結果的問題，從而提高水電機組振動預測精確度與可靠性。實驗結果證明提出的模型有效的提高了預測精度，取得了較好的預測結果。

1 基礎理論

1.1 一維卷積神經網絡

CNN 是典型的多層前饋神經網絡，常用于圖像處理領域，因它可以避免層間因完全連接而造成的參數冗余，通過局部的連接方式，降低了訓練的難度和對數據的依賴性。CNN 主要包含三種層：卷積層、池化層和全連接層。卷積層將特征向量經過卷積運算傳遞給池化層，池化層對數據進行降維處理，通過卷積層和池化層的交替使用能夠有效的提取數據局部特征并降低局部特征維度，經過多個卷積層池化層交替運算，最終，將得到的高級特征信息通過全連接層輸入下一層網絡進行下一步預測。通常，CNN 在處理二維圖像問題時需要三個維度的數據：寬度、高度和通道數。而一維CNN 可看作是輸入數據高度為1時的特殊情境。一維卷積運算如式（1）所示：

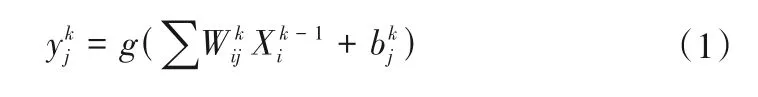
1.2 門控循環單元

GRU 是一種特殊的RNN，與LSTM 相比，它具有快速收斂和參數更少的優點，在保證預測性能的前提下，簡化了復雜的結構，提高了運算速度。因此，GRU 比LSTM 網絡更簡單、更有效。GRU結構如圖1所示。

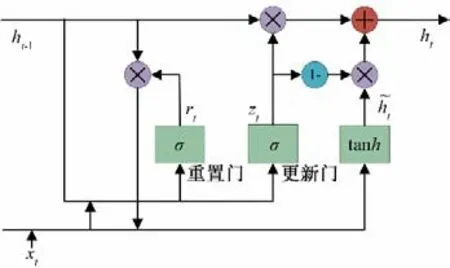
圖1 GRU網絡結構圖Fig.1 GRU network structure diagram

設xt為輸入，ht為隱藏層輸出，則GRU計算流程如下式：

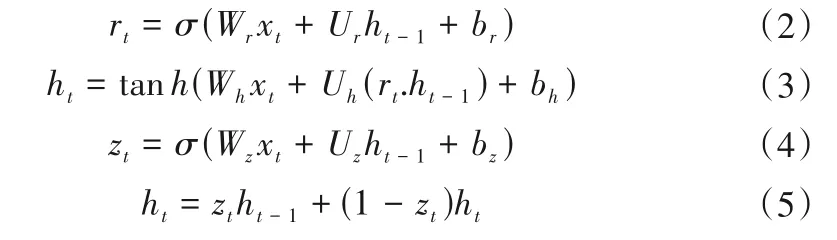
式中：rt為重置門；ht-1為前一時刻隱藏單元的輸出；σ為sigmoid的激活函數；Wr、Ur、br、Wh、Uh、bh、Wz、Uz、bz分別為可訓練的權重參數和偏置。

1.3 雙向門控循環單元

BiGRU 是GRU的改進，基于正反2層GRU神經網絡構造分別處理數據，即使用一個GRU 神經網絡來計算過去的信息，并同時使用另一個相同且方向相反的GRU來計算未來的信息，通過前向與反向的GRU 單元學習歷史與未來時刻對當前信息的影響。其結構如圖2所示。

圖2 BiGRU網絡結構圖Fig.2 BiGRU network structure diagram

2 CNN-BiGRU預測模型

CNN-BiGRU 組合預測模型網絡結構見圖3。本模型中保留了CNN 提取非線性特征能力并與BiGRU 處理長序列的數據挖掘能力相結合，從而避免有用信息丟失，發掘序列的長依賴性。

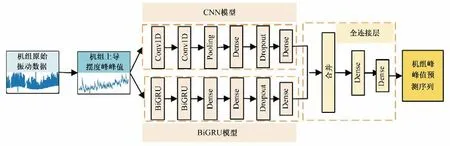
圖3 基于CNN-BiGRU組合預測模型Fig.3 Based on the CNN-BiGRU combination prediction model

2.1 CNN模型設計

水電機組振動信號具有強烈的非線性，而CNN 具有強大的非線性特征獲取能力，故由CNN 層提取相應特征進行學習預測。CNN 模型網絡中選用兩層重復卷積，目的是盡早提取到信號的高級特征，避免信號在通過池化層時失去重要特征；池化層選用最大池化操作，對卷積層所提取特征進行向下采樣，從而精簡模型參數；最后將數據輸入全連接層，CNN 中全連接層的作用是把池化后的特征向量進行重新組裝擬合，并通過激活函數增加模型的非線性能力，與其他激活函數相比，ReLU 輸出的特征具有稀疏性，使得網絡具有較好的泛化能力。此外，在輸入大于0時，ReLU的導數恒為1，使得網絡計算速度較快且不易出現梯度彌散。

2.2 BiGRU模型設計

水電機組振動信號機組振動信號本身具有時序關系，而Bi-GRU 在時序序列的預測中具有良好效果。BiGRU 網絡中選用兩層BiGRU 層，完成時序信息的有效提取，但當BiGRU 模型參數過多時，容易產生過擬合現象。為防止訓練過度，BiGRU 層采Dropout 機制，隨機丟棄一部分神經元節點使其暫時不參與模型訓練，使得BiGRU 網絡不會過度依賴部分特征提升模型的泛化能力。最后將處理后的數據輸入BiGRU的全連接層。

2.3 全連接層設計

數據經過CNN 模型和BiGRU 模型分別處理后并行拼接作為全連接層輸入，考慮到模型結構的非線性，構建了3 個Dense層，分別有32個16個和1個神經元，完成模型的輸出。

2.4 評價指標

將測試集輸入數據矩陣化處理后依次輸入訓練好的網絡中，將網絡的輸出與測試集的輸出數據進行比較，計算結果的平均絕對誤差（Mean Absolute Error，MAE），平均絕對百分誤差（Mean Absolute Percentage Error，MAPE）和均方根誤差（Root Mean Square Error，RMSE），計算公式如下所示：

式中：xi是真實值為模型輸出值；n為序列的長度。

3 實例分析

3.1 數據的選取與處理

相關研究表明，波形的標準差或峰峰值可以較好的反應機組的狀態［12-14］，因此本實驗中使用振動信號峰峰值作為實驗數據。本實驗以某電站3 號機組的上導X方向擺度與下導X方向擺度數據峰峰值作為研究對象，實際生產中，機組振擺采樣頻率較高，短時間會產生大量高密度數據［15］，為有效進行預測，為避免機組啟停時刻的異常值影響，研究選取機組2019年3月2日0 時至2019年9月1日0 時發電穩態（機組開機后一小時，停機前10 min）采集到的監測數據，選取時間間隔為5 min 的數據，最終選取機組穩態峰峰值共5 080 條，實驗中，選取前4 500條數據作為訓練集，后580條數據作為測試集。

首先將數據進行劃分為訓練集和測試集，后對數據進行歸一化處理，歸一到區間［0，1］中，歸一化公式：

式中：xmax，xmin分別為數據中的最大值和最小值。

3.2 訓練方法優選

為保證模型的訓練具有良好的精度與泛化能力，因此在網絡訓練中需要選取合適的參數，CNN-BiGRU 模型中的參數設置詳情如下：

（1）損失函數。損失函數用于評價模型訓練過程中真實值與預測值之間的差距，損失函數值越小，表示模型訓練時的表現越好。常見的損失函數主要包括：MAE和MSE等。而MSE是常用于回歸預測問題中的損失函數，因此，本文采用MSE作為CNN-BiGRU網絡的損失函數。

（2）網絡學習率與迭代次數。學習率控制了模型的訓練步長，決定了模型能否收斂與收斂的速度。在CNN-BiGRU 網絡中，通過試錯法網絡學習率為0.01，全連接層中dropout 值設置為0.2。

（3）優化算法。優化算法的正確使用可有效提升模型的訓練速度和預測精度。目前應用較多的優化算法有Adam、RMSprop、SGD，本文分別使用3 種優化算法對CNN-BiGRU 模型進行150 次訓練，實驗結果如圖4 所示。從圖4 中可以看出Adam訓練的網絡效果最好，RMSprop 則相對滯后，SGD 的效果最差。因此最終本模型選用Adam作為模型優化器。

圖4 優化算法對比Fig.4 Optimize algorithm comparison

3.3 實驗結果對比

為驗證所提方法的有效性，以上導擺度X向振動峰峰值數據分別多次訓練和測試模型，將其與GRU 模型、BiGRU 模型、CNN-GRU 并行網絡、CNN-LSTM 并行網絡進行對比分析，結果如表1 所示。根據預測結果可知，所提組合模型效果最佳，而CNN-LSTM 網絡效果最差。

從表1可以看出：

表1 上導擺度X向振動峰峰值預測結果對比Tab.1 The up-guided slew X is compared to the prediction results of vibration peaks and peaks

（1）所提組合模型相較于GRU、BiGRU 單一預測模型，MAE分別降低了53.09%、51.87%，MAPE 分別降低了52.83%、51.39%，RMSE 分別降低了64.28%、62.77%，可以看出當使用CNN 模塊提取數據特征后，水電機組振動峰峰值預測精度大幅提升，這表明并聯CNN 模塊可有效提升水電機組振動信號的預測精度。

（2）所提組合模型相較于CNN-GRU、CNN-LSTM 組合預測模型，MAE分別降低了49.05%、56.86%，MAPE 分別降低了48.42%、56.22%，RMSE 分別降低56.76%、64.35%，這表明了采用BiGRU 同時學習未來和歷史信息，可以增強模型的對時間序列的學習能力，使得預測的更加準確。

本實驗所提模型與對比模型在相同工況下的上導擺度X方向上的測試結果如圖5、6所示?？梢钥闯鰧Ρ饶Ｐ皖A測結果整體趨勢與實際值保持一致，但是局部誤差較大。而CNN-BiGRU 模型預測結果可表示出真實值的整體趨勢與局部特征的變化，除個別極值點外，模型的預測值與實際值基本吻合，可最大程度的反映水電機組振動的波動情況。

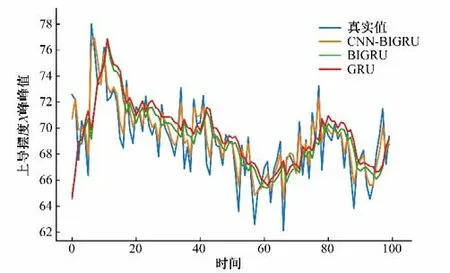
圖5 上導擺度X方向本模型與單一模型預測對比圖Fig.5 The up-guided slew X direction of this model is compared with the single model prediction

為進一步證明所提模型的有效性，將各模型應用于下導擺度X向振動峰峰值預測。圖7、8展示了所提模型與對比模型在相同工況下的下導擺度X方向上的多次測試結果。表2展示了不同模型對下導擺度X方向的預測結果，可以看出CNN-BiGRU 模型相較于其他模型預測精度更高，誤差更小。證明了該模型在機組振動預測方向上的優越性。

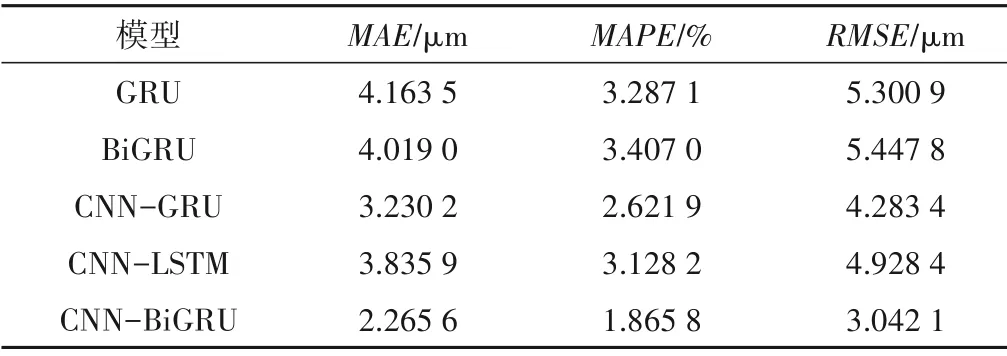
表2 下導擺度X向振動峰峰值預測結果對比Tab.2 The hemline X contrasts with the prediction results of vibration peaks and peaks

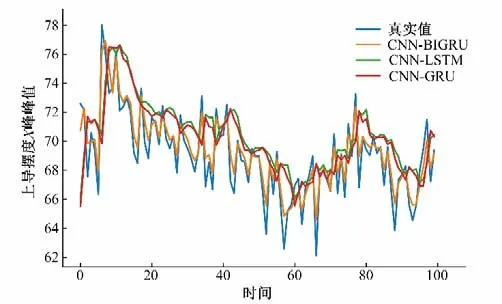
圖6 上導擺度X方向與組合模型預測對比圖Fig.6 The up-guided slew X direction of this model is compared with the combined model prediction

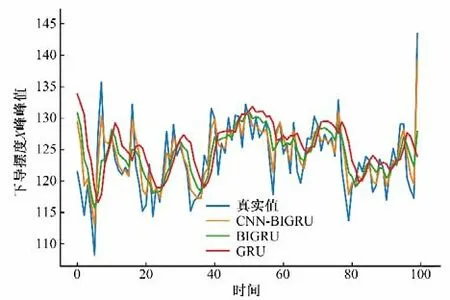
圖7 下導擺度X方向本模型與單一模型預測對比Fig.7 Hemline X direction This model compares with a single model prediction

4 結 語

針對水電機組振動信號非平穩和非線性問題，提出一種基于CNN-BiGRU 組合模型的水電機組振動預測方法，首先利用CNN 提取數據有效局部特征，再運用BiGRU 模型處理時序性特征數據，深度挖掘水電機組振動數據的非線性以及時序性特征。通過與傳統預測模型進行對比，結果表明本文提出的混合模型有更高的預測精度，證明該模型可充分提取輸入數據的特征并利用數據的時序性特征進行振動信號預測。

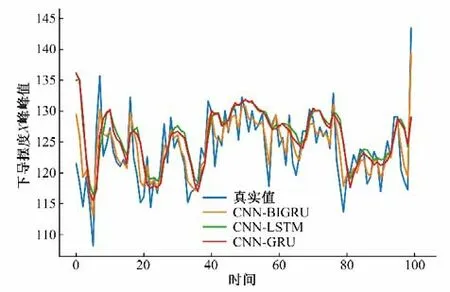
圖8 下導擺度X方向與組合模型預測對比圖Fig.8 Hemline X direction This model compares with the combined model prediction