面向計算思維的可視化編程活動設(shè)計與應(yīng)用*

王 靖 馬志強 劉亞琴 杜鴻羽

面向計算思維的可視化編程活動設(shè)計與應(yīng)用*

王 靖1馬志強1[通訊作者]劉亞琴2杜鴻羽1

（1．江南大學 江蘇“互聯(lián)網(wǎng)+教育”研究基地，江蘇無錫 214122；2．蘇州市吳中區(qū)東山中學，江蘇蘇州 215107）

計算思維是21世紀公民應(yīng)具備的重要素養(yǎng)，而可視化編程活動有助于發(fā)展中小學生的計算思維。文章采用基于設(shè)計的研究方法，提出可視化編程活動的設(shè)計原則，即設(shè)計問題驅(qū)動的編程任務(wù)、采用腳本支持的小組配對編程、支持編程過程的可視化表征。之后，文章將程序設(shè)計與小學數(shù)學結(jié)合的跨學科主題作為學習內(nèi)容，通過包含“設(shè)計→實施→評價”路徑的三輪迭代，從數(shù)學學業(yè)成績、計算思維水平兩個角度衡量迭代的效果，最終確定了對應(yīng)于三條設(shè)計原則的十條具體策略；同時，驗證了可視化編程活動對計算思維中的計算概念、計算實踐、計算觀點三個維度有統(tǒng)計學意義上的顯著作用。文章進行的實證研究，可為計算思維的培養(yǎng)研究與實踐提供原則指導和策略參考，且經(jīng)過實證迭代、確定的原則和策略，能夠豐富計算思維研究領(lǐng)域的理論體系。

計算思維；可視化編程；小學數(shù)學；編程教學

引言

當前，計算思維正逐漸與讀、寫一樣成為公民必備的核心素養(yǎng)[1]。計算思維的本質(zhì)在于將一個復雜問題解構(gòu)，通過抽象、分解、模式識別、遷移等過程找到解決問題的有效方法[2][3]。編程活動可訓練學生分解復雜問題、規(guī)劃解決方案并用代碼實現(xiàn)方案的能力，是發(fā)展計算思維的有效手段[4]。因此，通過編程課程培養(yǎng)計算思維已成為國內(nèi)外中小學計算思維培養(yǎng)的重要途徑。然而，在編程課程中培養(yǎng)計算思維常面臨兩個實踐問題：①低齡學生的認知門檻問題。將計算思維培養(yǎng)中最核心的“問題解決”步驟轉(zhuǎn)化為計算機程序指令，需掌握相應(yīng)的編程語言，但中小學生往往很難理解其包含的復雜語法規(guī)則和抽象符號形式。②教師的教學重心問題。在編程教學活動設(shè)計中，教師可能會重點關(guān)注學生對程序符號和語法規(guī)則的學習，而忽視計算思維的發(fā)展[5]。可視化編程活動能夠?qū)崿F(xiàn)程序設(shè)計的“所見即所得”，從而有效解決上述問題。此外，可視化編程活動呈現(xiàn)出的“低門檻、高天花板”特征，對于發(fā)展計算思維具有重要價值[6]。

當前，可視化編程的具體實施策略主要有：利用可視化編程套件工具設(shè)計教學[7]、將計算思維培養(yǎng)融入可以外顯化的任務(wù)等。但由于可視化編程活動的設(shè)計尚缺少原則指導和策略依據(jù)，導致可視化編程任務(wù)往往預設(shè)了問題解決路徑，卻難以幫助學生發(fā)展問題解決能力[8]。因此，本研究采用基于設(shè)計的研究方法來發(fā)展活動設(shè)計的基本原則及實施策略，重在探討以下三個問題：①面向計算思維發(fā)展的可視化編程活動的設(shè)計原則與策略是什么？②如何迭代改進可視化編程活動的設(shè)計策略？③可視化編程活動對于計算思維發(fā)展的效果怎樣？

一 研究設(shè)計

1 研究情境與對象

本研究在我國華東地區(qū)的一所農(nóng)村小學開展，參與研究的是該校三、四年級的32名學生，其中男生有18名、女生有14名。這些學生參與本研究之前沒有編程經(jīng)驗，整個研究過程持續(xù)了18周。課程學習內(nèi)容分為三個模塊：可視化編程Scratch與圖形繪制、熊貓?zhí)准c距離感知、micro:bit機器人與數(shù)據(jù)整理。

2 研究過程

本研究遵循基于設(shè)計的研究方法，制定了基于設(shè)計的研究流程（如圖1所示），包含設(shè)計、實施、評價三個相互聯(lián)系的環(huán)節(jié)：①在設(shè)計環(huán)節(jié)，主要是結(jié)合文獻分析和學情分析，基于設(shè)計原則與對應(yīng)的策略進行可視化編程的活動設(shè)計；②在實施環(huán)節(jié)，主要是通過三輪跨學科教學實踐，將設(shè)計出來的活動用于支持學生的數(shù)學知識學習并提升其編程知識技能，進而發(fā)展學生的計算思維水平；③在評價環(huán)節(jié)，主要是結(jié)合每一輪實證的過程和結(jié)果，對活動設(shè)計策略進行反思和修改，并檢驗可視化編程活動在本輪的應(yīng)用效果，以不斷迭代改進相關(guān)的策略。在每一輪實證結(jié)束后，研究者通過課堂觀察、訪談，對活動設(shè)計進行反思與改進；同時，通過常規(guī)測試、問卷調(diào)查，對學習者在本輪活動結(jié)束后的數(shù)學學業(yè)成績和計算思維水平進行評價。在所有迭代輪次完成后，研究者開展總結(jié)性評價。

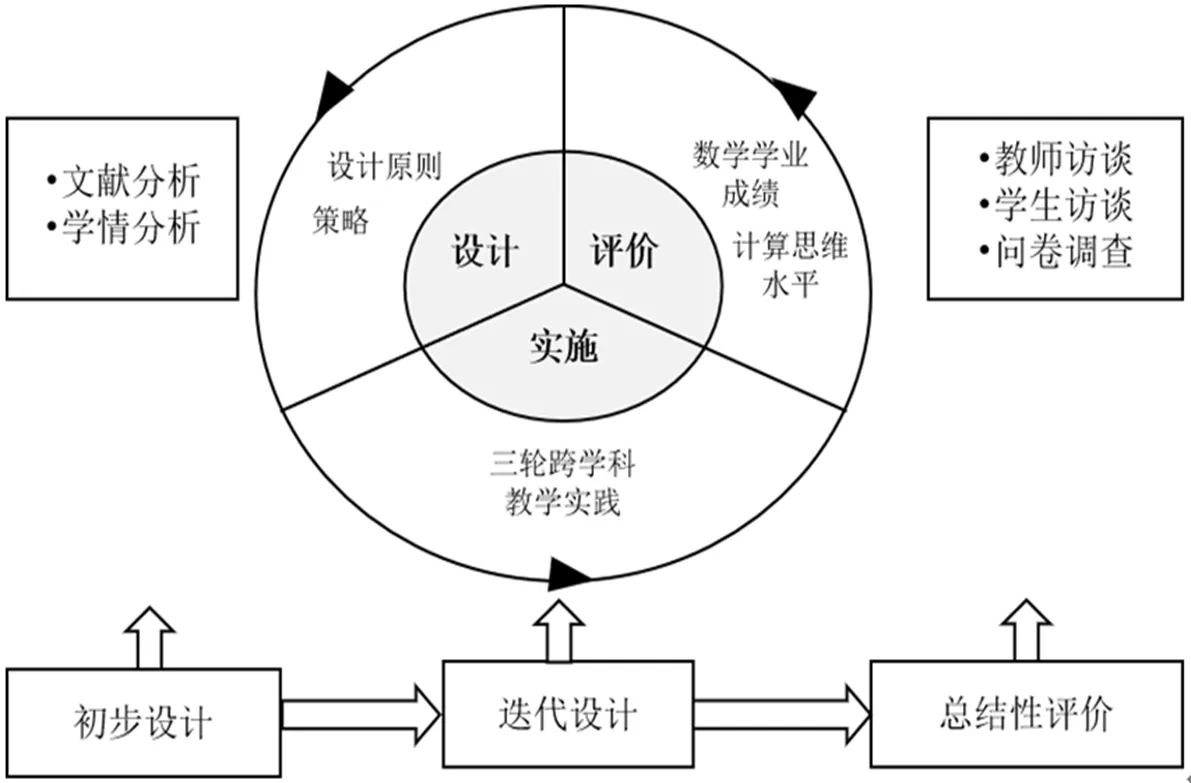
圖1 基于設(shè)計的研究流程

需要說明的是，對于數(shù)學學業(yè)成績，本研究是利用數(shù)學統(tǒng)考試題得分（即標準化后的成績）來評價。而對于計算思維水平，本研究參考Brennan等[9]基于交互式編程提出的“計算思維的三維框架”來評價。“計算思維的三維框架”包含三個維度：①計算概念，是指在編程中使用的概念；②計算實踐，是指在編程中解決問題；③計算觀點，是指學生對自己、自己與他人的關(guān)系、周圍技術(shù)世界的理解。本研究采用這三個維度，來評價學生的計算思維水平。其中，“計算概念”“計算實踐”這兩個維度是依據(jù)Bebras競賽題進行評價——Bebras競賽題是一系列簡短的問題或任務(wù)，針對年級劃分題目；而“計算觀點”維度是采用計算觀點量表進行評價——此量表是在Korkmaz等[10]開發(fā)的計算思維水平量表的基礎(chǔ)上修訂而成。

二 面向計算思維的可視化編程活動設(shè)計原則與設(shè)計框架

活動理論提出，活動系統(tǒng)包含工具、規(guī)則、分工、主體、客體、共同體六個互動要素，這些要素構(gòu)成三角形架構(gòu)，其中工具、規(guī)則、分工分別為三角形的三個頂點，三個要素之間兩兩相關(guān)；主體、客體、共同體處于三角形三條邊的中點位置；六個要素共同構(gòu)成了生產(chǎn)、交流、分配、消耗四個子系統(tǒng)[11]。以此為參考，本研究確定了可視化編程活動的六個要素：可視化編程工具、問題、角色、學習者、任務(wù)、配對小組。其中，學習者、配對小組這些“人”的要素與問題之間的互動，構(gòu)成了問題解決子系統(tǒng)；任務(wù)、配對小組、角色這三個要素有利于學習者形成相互依賴、互相影響的協(xié)作關(guān)系[12]，由此形成任務(wù)協(xié)作分工子系統(tǒng)；而可視化編程工具、學習者、任務(wù)之間的互動，形成了任務(wù)執(zhí)行子系統(tǒng)。結(jié)合這三個子系統(tǒng)正常運作所需具備的條件，并圍繞計算思維的計算概念、計算實踐、計算觀點三個維度，本研究提出了三條設(shè)計可視化編程活動的基本原則：設(shè)計問題驅(qū)動的編程任務(wù)、采用腳本支持的小組配對編程、支持編程過程的可視化表征。依托上述三條設(shè)計原則，本研究構(gòu)建了面向計算思維的可視化編程活動設(shè)計框架，如圖2所示。其中，三條設(shè)計原則是該框架的核心內(nèi)容。

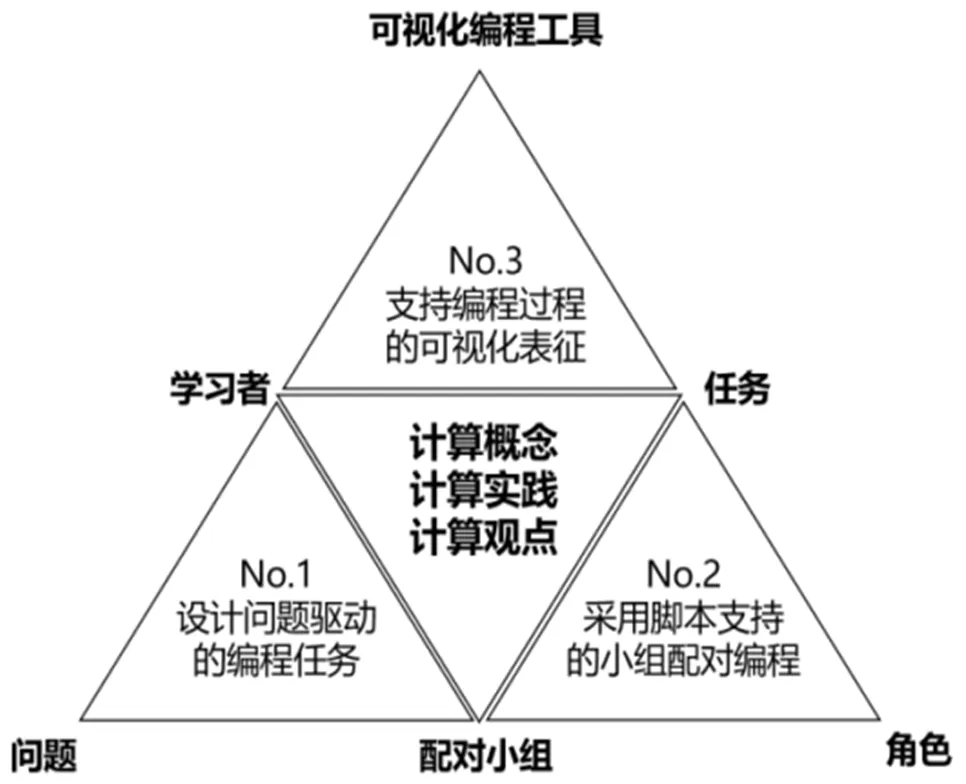
圖2 面向計算思維的可視化編程活動設(shè)計框架

1 設(shè)計問題驅(qū)動的編程任務(wù)

計算思維以“問題解決”為核心內(nèi)涵，問題解決能力需在嵌入真實情境的劣構(gòu)問題解決過程中加以鍛煉，引導學生完成由感性認知到理性認知的升華。同時，為凸顯問題解決的進階性，研究者要設(shè)計不同難度層級的問題和任務(wù)。基于此，對應(yīng)于本條原則的具體實施策略是：①以學科知識為核心，設(shè)計編程任務(wù)情境；②將一個復雜編程問題分解為線型問題，或?qū)栴}多角度表述為樹型問題；③將每種問題對應(yīng)于封閉式、半開放式、完全開放式三種編程任務(wù)。

2 采用腳本支持的小組配對編程

劉敏等[13]指出，結(jié)對編程（同本研究的“配對編程”）為結(jié)對雙方提供了在社會互動中建構(gòu)意義的機會，加快了即時反饋的頻率和效率，有利于學習并掌握計算思維邏輯。因此，在計算思維培養(yǎng)方面，配對編程是一種較好的學習方式。配對編程的本質(zhì)是一種協(xié)作學習形式，而在成功的協(xié)作互動中，成員之間需要具備積極的相互依賴關(guān)系[14]。基于此，配對編程通過“駕駛員”與“導航員”兩個角色的切換，為參與編程的兩位學生安排均等且合理的任務(wù)。

但對于小學生來說，如何實現(xiàn)高效協(xié)同是配對編程活動設(shè)計要考慮的關(guān)鍵問題。對此，本研究采用協(xié)作腳本，為研究對象——32名小學生提供協(xié)作的規(guī)范與步驟上的詳細指導。具體來說，研究者要在配對編程前明確組內(nèi)的角色分配與任務(wù)協(xié)作，并利用組內(nèi)的積極交流幫助小學生保持對編程活動的注意力與專注力，相應(yīng)的實施策略是：①通過配對編程核查表（“腳手架”的具體表現(xiàn)形式）分配任務(wù)；②規(guī)定“駕駛員”與“導航員”兩個角色并定期進行角色切換。

3 支持編程過程的可視化表征

計算思維形成的過程，蘊含從具體情境中剔除特定情境、剝離并抽象出問題本質(zhì)和解決模型的過程。但對于年齡偏低的小學生來說，這恰恰是整個思維培養(yǎng)過程中的難點。諸多關(guān)于計算思維培養(yǎng)的成熟研究表明：可視化編程可以降低代碼語句編寫、代碼語法理解等技術(shù)難度，使教師有更多精力聚焦于計算思維的培養(yǎng)和能力的發(fā)展[15]；從配對編程的角度，知識的可視化表征可以幫助協(xié)作成員建立觀點間的關(guān)聯(lián)，以便于其整合共同觀點[16]。基于此，本研究將支持編程過程的可視化表征定為第三條設(shè)計原則。本研究涉及的編程過程主要包括對問題關(guān)鍵概念的識別與表征、問題解決步驟的分步與執(zhí)行、代碼的生成與調(diào)試，具體的實施策略為：①采用積木式代碼可視化表征抽象和模式識別后的編程概念；②通過算法執(zhí)行步驟的分解和重構(gòu)可視化表征完整的問題解決過程。

三 面向計算思維的可視化編程活動迭代及其效果

為了將上述原則和策略付諸實踐并加以優(yōu)化，本研究開展了三輪可視化編程活動的設(shè)計、實施與評價。如前所述，計算思維的核心是：問題解決能力需在嵌入真實情境的劣構(gòu)問題解決過程中加以鍛煉。而在編程課程中設(shè)計劣構(gòu)問題，往往需要結(jié)合其他學科的知識。因此，根據(jù)本研究中編程教學的具體內(nèi)容，本研究選擇與數(shù)學學科相結(jié)合設(shè)計問題情境。

1 第一輪設(shè)計與實施

（1）設(shè)計階段

首先，根據(jù)“設(shè)計問題驅(qū)動的編程任務(wù)”這一原則及其具體實施策略，本輪實證中研究者和任課教師明確了：①本輪教學實踐的總?cè)蝿?wù)為“雪花圖形繪制”；②將上述總?cè)蝿?wù)分解為四周的任務(wù)，并按照線型、樹型問題驅(qū)動每一周的編程任務(wù)；③每種問題對應(yīng)于封閉式、半開放式、完全開放式三種編程任務(wù)。

隨后，根據(jù)“采用腳本支持的小組配對編程”這一原則及其相應(yīng)的實施策略，研究者和任課教師明確了：①通過《Scratch配對編程手冊》與核查表，進行清晰的角色、任務(wù)分配；②規(guī)定“駕駛員”與“導航員”兩個角色完成一個任務(wù)后進行角色切換。

最后，根據(jù)“支持編程過程的可視化表征”這一原則及其具體的實施策略，研究者和任課教師進行了如下設(shè)計：①采用Scratch積木式代碼，表征抽象和模式識別后的編程概念；②通過算法執(zhí)行步驟的分解和重構(gòu)，表征完整的問題解決過程，并將之不斷優(yōu)化。

（2）實施階段

本輪選取的數(shù)學學習內(nèi)容為“幾何圖形繪制”，具體包括角度、坐標、變量、運算概念與平面圖形的簡單繪制、直角平面圖形的周長和面積計算、雪花圖形的繪制。教學目標是掌握數(shù)學與Scratch編程概念，如長度、周長、面積、角度、順序、循環(huán)、事件、并行、條件、運算符、變量；同時，掌握基本的圖形概念與周長、面積的計算公式，并學會使用簡單程序編寫圖形繪制任務(wù)的邏輯代碼。

在第一輪學習活動開始之前，研究者對參與本實證研究的32名小學生進行兩兩組合，并介紹活動過程中要定期切換角色、按照核查表逐項核查進度等注意事項。在第一周教學中，教師引導學生觀賞最終的雪花圖形，之后將完成這一作品所需要的步驟、任務(wù)和知識點進行分解并向?qū)W生展示，讓學生熟悉“雪花圖形繪制”的學習內(nèi)容及其各周安排。具體來說，第一周的學習內(nèi)容為認識不同顏色積木塊的功能；第二周的學習內(nèi)容為坐標與角度的學習、平面圖形的繪制；而第三周至第四周的學習內(nèi)容為變量與運算的學習、直角平面圖形的周長和面積計算。

在第一輪評價中，數(shù)學學業(yè)成績、計算思維水平的量化數(shù)據(jù)分析結(jié)果顯示：前后測數(shù)據(jù)變化均有提升，但均未達到統(tǒng)計學意義上的顯著水平——這說明計算思維的培養(yǎng)并非短期內(nèi)就能取得明顯效果，同時也提示研究者：低齡學生的計算思維從一個較低水平取得進步是有可能的，但要發(fā)生質(zhì)變需經(jīng)過長期的培養(yǎng)。而課堂觀察數(shù)據(jù)分析與訪談結(jié)果顯示：可視化編程活動提升了學生的協(xié)作能力、學習動機和興趣。對于小學生來說，采用可視化編程的方式將原本抽象的概念圖形化，對相關(guān)知識點就更容易理解和上手了，并能快速進入任務(wù)學習中。

值得注意的是，課程學習過程中也出現(xiàn)了一些問題，如少數(shù)配對小組存在“霸鼠標”“搭便車”等現(xiàn)象，原因主要在于這些小組的配對成員能力水平差異過大；課上學生此起彼伏地喊“老師”現(xiàn)象嚴重，這是因為完成任務(wù)作品之后，學生需得到教師的評價與肯定才會進行下一任務(wù)——此現(xiàn)象的背后，反映出的問題是教師反饋延遲與反饋不足。另外，訪談結(jié)果表明，學生認為“導航員”角色如同虛設(shè)，相應(yīng)地，采用配對編程核查表這一腳手架形式并沒有發(fā)揮作用。

基于上述評價結(jié)果，研究者和任課教師對可視化編程活動設(shè)計策略進行了補充和調(diào)整：根據(jù)“設(shè)計問題驅(qū)動的編程任務(wù)”原則，補充“加入教師的實時反饋支架”策略，此支架主要起督促角色切換、實時反饋任務(wù)的完成程度兩個作用；根據(jù)“采用腳本支持的小組配對編程”原則，做出“取消原策略中‘核查表’的設(shè)計，用《Scrach配對編程手冊》實現(xiàn)這一功能”的策略調(diào)整。

2 第二輪設(shè)計與實施

（1）設(shè)計階段

在進行第二輪設(shè)計時，研究者做出的改進包括：①通過配對編程手冊與熊貓?zhí)准拿鞔_分工，保證清晰的角色和任務(wù)分配，并保證所有編程過程可視化；②配對小組的兩名學生將被助教督促定期切換彼此的角色。

（2）實施階段

第二輪的學習主題為“概念感知”，旨在將出現(xiàn)在各種數(shù)學問題情境中的抽象概念與其在日常生活中的具體表征相匹配，引導學生對分貝、溫度、距離等概念進行感知。教學目標是讓學生掌握相關(guān)抽象概念，學會熊貓?zhí)准慕M裝與編程語言，能夠自行設(shè)計感知任務(wù)的代碼片段。

研究者將學習內(nèi)容分成熟悉熊貓?zhí)准⒅谱髀暱責簟⒅谱鞲袘?yīng)風扇、制作距離報警器四個相對獨立的模塊。在后三個模塊的每一節(jié)課中，學生既要鍵入代碼，也要組裝套件，通過這兩個任務(wù)完成每一個模塊的學習：通過聲控燈的制作，完成對“分貝”這一概念的感知；通過感應(yīng)風扇的制作，來感知“溫度”這一概念；通過利用超聲波測距離的操作，來實現(xiàn)對“距離”這一概念的感知。在整個學習過程中，教師會設(shè)計問題支架對學生進行任務(wù)分解方面的引導。

蟲力黑驅(qū)蟲后2 d、6 d，分別進行觀察，對體虱的成蟲特效，對幼蟲的效果觀察不到，但30 d后幼蟲發(fā)育成成蟲，牧民還需要再灌服1次蟲力黑，才能達到效果。

（3）評價階段

在第二輪評價中，數(shù)學學業(yè)成績、計算思維水平的量化數(shù)據(jù)分析結(jié)果顯示：前后測數(shù)據(jù)變化仍未達到統(tǒng)計學意義上的顯著水平。課堂觀察顯示，教師的督促與協(xié)調(diào)保證了角色的定期切換；但存在因?qū)W生得意地向周圍小組展示自己的作品而使課堂變得嘈雜的問題，其背后癥結(jié)在于本輪設(shè)計缺少合理的組間交流支持；此外，創(chuàng)客套件的使用與損壞情況嚴重。訪談結(jié)果表明，學生認為組裝套件比填寫核查表有趣；但進行完全開放式任務(wù)時，需要教師提供一些可能線索。

基于上述評價結(jié)果，研究者和任課教師對可視化編程活動設(shè)計策略進行了補充和調(diào)整：根據(jù)“設(shè)計問題驅(qū)動的編程任務(wù)”原則，將“加入教師的實時反饋支架”策略調(diào)整為“教師需要提供關(guān)于任務(wù)評價與任務(wù)障礙的即時反饋支架”，補充“完全開放式任務(wù)需要教師提供可能線索”的策略；根據(jù)“采用腳本支持的小組配對編程”原則，補充“為學生提供組間交流平臺”的策略，并將“通過配對編程核查表分配任務(wù)”策略調(diào)整為“通過《Scrach配對編程手冊》與編程工具進行任務(wù)與角色分配”；根據(jù)“支持編程過程的可視化表征”原則，補充“通過編程工具對協(xié)作角色進行可視化”的策略。

3 第三輪設(shè)計與實施

（1）設(shè)計階段

在進行第三輪設(shè)計時，研究者做出的改進包括：①導航員對micro:bit機器人的運動進行觀察與記錄；②增加利用出聲思維法（即出聲說出自己的思考過程）進行小組展示；③采用micro:bit機器人支持配對角色的有形分配。

（2）實施階段

第三輪聚焦于數(shù)學課本中的“統(tǒng)計與概率”模塊，設(shè)計的主題為“數(shù)據(jù)整理”，旨在引導學生對數(shù)據(jù)進行收集、整理與表征。教學目標是讓學生學會micro:bit機器人的編程語言，并掌握數(shù)據(jù)整理的一般步驟，如收集、整理、分析、圖形表征等。

以“繪制小車設(shè)置速度與實際速度之間的關(guān)系圖”一節(jié)為例，教師首先和學生一起完成小車按照事先設(shè)計好的代碼前進并實現(xiàn)超聲波測距的過程，引導學生學習小車前進的距離、速度、超聲波測距。接著，教師帶領(lǐng)學生回憶前一周學習的控制小車前進、實現(xiàn)超聲波測距的代碼。之后，教師帶領(lǐng)學生完成連接主板的過程，并開始配對編程；同時，教師根據(jù)《Scrach配對編程手冊》為學生提供詳細指導。最后，同伴采用出聲思維的形式進行分享，這種分享也是小組在其他同學面前詳細展示其思考過程和成果。

（3）評價階段

為系統(tǒng)評價可視化編程活動對數(shù)學學業(yè)成績的影響，本研究將第三輪學生的數(shù)學學業(yè)成績與前兩輪進行了配對樣本t檢驗，結(jié)果如表1所示。可以看出，與第一輪、第二輪相比，第三輪學生的數(shù)學學業(yè)成績得分均獲得了顯著性提升（=0.000，=0.005），表明可視化編程活動對于提升數(shù)學學業(yè)成績有正向影響。

表1 數(shù)學學業(yè)成績的配對樣本t檢驗（N=32）

MeanSDtSig.(2-tailed) 第二輪和第三輪對比第二輪0.680.27-5.2200.000 第三輪0.950.29 第一輪和第三輪對比第一輪0.730.33-3.0190.005 第三輪0.950.29

將第三輪Bebras競賽題（用于評價“計算概念”“計算實踐”）得分與第一輪、第二輪的相應(yīng)得分進行配對樣本t檢驗，結(jié)果如表2所示。可以看出，與前兩輪相比，第三輪Bebras競賽題得分均有顯著性提高（=0.007，=0.007），表明經(jīng)過一段較長時間的實踐后，學生在“計算概念”“計算實踐”兩個維度上的計算思維水平得到了顯著提升。

表2 Bebras競賽題得分的配對樣本t檢驗（N=32）

MeanSDtSig.(2-tailed) 第二輪和第三輪對比第二輪4.530.92-2.8880.007 第三輪5.191.06 第一輪和第三輪對比第一輪4.281.67-2.9020.007 第三輪5.191.06

對第三輪采用計算觀點量表（用于評價“計算觀點”）獲得的計算觀點得分與第一輪、第二輪的相應(yīng)得分進行配對樣本t檢驗，結(jié)果如表3所示。可以看出：與前兩輪比較，第三輪計算觀點得分均有顯著性提高（=0.032，=004），表明經(jīng)過幾輪迭代后，學生在“計算觀點”維度上的計算思維水平也得到了顯著性提升。

表3 計算觀點得分的配對樣本t檢驗（N=32）

MeanSDtSig.(2-tailed) 第二輪和第三輪對比第二輪4.260.46-2.2390.032 第三輪4.440.46 第一輪和第三輪對比第一輪4.060.70-3.1170.004 第三輪4.440.46

值得注意的是，部分數(shù)據(jù)反映的計算思維水平在第二輪實證研究后，與第一輪相比并沒有得到顯著性提升，這正是計算思維培養(yǎng)與提升具有長期性的表征。而課堂觀察顯示，教師對無法跟上整體進度的小組進行額外輔導，能夠幫助配對小組取得進步；micro:bit智能小車能夠營造情境性，增加了學生的真實體驗感。此外，本研究采用的發(fā)聲思維方式能夠有效幫助配對編程小組梳理思路、深度反思。總之，經(jīng)過前兩輪實證研究中設(shè)計原則、實施策略的迭代與應(yīng)用，第三輪實證后得到的學生數(shù)學學業(yè)成績、計算思維等結(jié)果均呈現(xiàn)出顯著優(yōu)于前兩輪的狀態(tài)。

四 研究總結(jié)與未來展望

1 對三個研究問題的回應(yīng)

針對研究問題一“面向計算思維發(fā)展的可視化編程活動的設(shè)計原則與策略是什么”，三輪迭代后最終凝練出面向計算思維發(fā)展的可視化編程活動的設(shè)計原則與策略，如表4前兩列所示。

針對研究問題二“如何迭代改進可視化編程活動的設(shè)計策略”，本研究通過“設(shè)計→實施→評價”路徑對活動設(shè)計的具體策略進行迭代，并從數(shù)學學業(yè)成績、計算思維水平兩個角度衡量迭代的效果，再結(jié)合師生訪談數(shù)據(jù)對策略進行逐輪次修改。在策略迭代過程中，研究者得到的啟示如表4第三列所示。

針對研究問題三“可視化編程活動對于計算思維發(fā)展的效果怎樣”，本研究通過實證研究發(fā)現(xiàn)可視化編程活動對計算思維中的計算概念、計算實踐、計算觀點三個維度有統(tǒng)計學意義上的顯著作用，同時也得出“低齡學生的計算思維要經(jīng)過長期的培養(yǎng)才能發(fā)生質(zhì)變”的結(jié)論。

表4 可視化編程活動的設(shè)計原則、策略及其迭代過程中的啟示

設(shè)計原則策 略策略迭代過程中的啟示 設(shè)計問題驅(qū)動的編程任務(wù)①以學科知識為核心，設(shè)計編程任務(wù)情境；②將一個復雜編程問題分解為線型問題，或?qū)栴}多角度表述為樹型問題；③將每種問題對應(yīng)于封閉式、半開放式、完全開放式三種編程任務(wù)，其中完全開放式編程任務(wù)需要教師提供可能線索；④教師需要提供關(guān)于任務(wù)評價與任務(wù)障礙的即時反饋支架。問題的進階設(shè)計是保障學生由淺入深思考問題解決策略、逐步形成計算思維的關(guān)鍵。這就意味著在設(shè)計編程任務(wù)中的問題時，要考慮問題的結(jié)構(gòu)及其分解策略。 采用腳本支持的小組配對編程①通過《Scrach配對編程手冊》與編程工具進行任務(wù)與角色分配；②規(guī)定“駕駛員”與“導航員”兩個角色并定期進行角色切換，同時輔以助教督促；③為學生提供組間交流平臺。計算思維可以通過社會化互動得到發(fā)展。參與配對編程的學生構(gòu)成小型的學習共同體，通過外在的對話與編程行為互動推動內(nèi)在的認知加工。對于低齡學生而言，這種外在的互動需要借助腳本、腳手架等干預進行規(guī)范。 支持編程過程的可視化表征①采用積木式代碼表征抽象和模式識別后的編程概念；②通過算法執(zhí)行步驟的分解和重構(gòu)表征完整的問題解決過程；③通過編程工具對協(xié)作角色進行可視化。可視化編程的核心作用機制是培養(yǎng)學生對問題解決模式的應(yīng)用與具象能力，以及根據(jù)可視化結(jié)果對問題解決模式的抽象概括能力。

2 研究未來展望

盡管本研究設(shè)計的面向計算思維的可視化編程活動背后的知識源于數(shù)學學科，但在設(shè)計問題情境的時候融入了大量科學與工程情境，如果學生缺少相應(yīng)的科學知識，僅靠數(shù)學和編程知識是無法完成活動的。這是本研究在跨學科設(shè)計上存在的不足。與此相應(yīng)，設(shè)計更具跨學科屬性的STEAM理念下的可視化編程活動，是本研究未來的發(fā)展方向。

[1][2][15]Wing J M. Computational thinking[J]. Communications of the ACM, 2006,(3):33-35.

[3]Yadav A, Hong H, Stephenson C. Computational thinking for all: Pedagogical approaches to embedding 21st century problem solving in K-12 classrooms[J]. TechTrends, 2016,60:565-568.

[4][5]Chao P Y. Exploring students’ computational practice, design and performance of problem-solving through a visual programming environment[J]. Computers & Education, 2016,(4):202-215.

[6][8]郁曉華,肖敏,王美玲,等.基于可視化編程的計算思維培養(yǎng)模式研究——兼論信息技術(shù)課堂中計算思維的培養(yǎng)[J].遠程教育雜志,2017,(6):12-20.

[7]Wang D, Wang T, Liu Z. A tangible programming tool for children to cultivate computational thinking[J]. The Scientific World Journal, 2014,(3):1-10.

[9]Brennan K, Resnick M. New frameworks for studying and assessing the development of computational thinking[A]. Proceedings of the 2012 annual meeting of the American Educational Research Association[C]. Vancouver: AERA, 2012:1-25.

[10]Korkmaz ?, ?akir R, ?zden M Y. A validity and reliability study of the computational thinking scales(CTS)[J]. Computers in Human Behavior, 2017,72:558-569.

[11]朱珂,楊冰,高晗蕊,等.活動理論指導下的STEM學習活動模型研究[J].現(xiàn)代教育技術(shù),2017,(11):33-38.

[12]馬志強.從相互依賴到協(xié)同認知——信息化環(huán)境下的協(xié)作學習研究[M].北京:中國社會科學出版社,2019:20.

[13]劉敏,汪瓊.結(jié)對編程:中小學編程教育的首選教學組織形式[J].現(xiàn)代教育技術(shù),2022,(3):102-109.

[14]馬志強.社會認知互動的多維刻畫:協(xié)作學習投入理論構(gòu)建與實踐探索[M].北京:中國社會科學出版社,2021:7.

[16]馬志強,李慧雯,王文秋,等.跨學科協(xié)作學習何以有效——STEM教育中CSCL應(yīng)用效果的元分析[J].現(xiàn)代遠程教育研究,2021,(1):97-104.

Design and Application of Visual Programming Activities towards Computational Thinking

WANG Jing1MA Zhi-qiang1[Corresponding Author]LIU Ya-qin2DU Hong-yu1

Computational thinking is a necessary literacy for citizens in the 21st century, and visual programming activities help to develop primary and middle school students’ computational thinking. Using the design-based research approach, this paper proposed the design principles of visual programming activities, namely designing problem-driven programming tasks, using script-supported group pair programming, and supporting visual representations of the programming process. After that, taking the interdisciplinary theme of combining programming and elementary school mathematics as learning content, this paper measured the iteration effect of from two perspectives of mathematics academic performance and computational thinking level, and further determined ten specific strategies corresponding to the three design principles, through three rounds of iteration including the “design→implementation→evaluation” path. At the same time, it was verified that visual programming activities had statistically significant effects on the three dimensions of computing concept, computing practice and computing viewpoint in computing thinking. The empirical research in this paper can provide principle guidance and strategy reference for the research and practice of computational thinking cultivation, and the determined principles and strategies after empirical iteration can enrich the theoretical system in the research field of computational thinking.

computational thinking; visual programming; primary school mathematics; programming teaching

G40-057

A

1009—8097（2022）09—0055—09

10.3969/j.issn.1009-8097.2022.09.006

本文為國家社會科學基金教育學青年課題“跨學科教育中的協(xié)同概念轉(zhuǎn)變研究”（項目編號：CCA190260）的階段性研究成果。

王靖，副教授，博士，研究方向為學習科學與技術(shù)，郵箱為jing850902@sina.com。

2022年1月15日

編輯：小米