財政補貼的供應鏈決策效率與社會福利研究

盧光熙

（江西財經大學 財稅與公共管理學院，江西 南昌 330013）

一、引言

隨著環境保護意識和可持續發展觀念的逐漸增強，以廢舊產品為原材料的再制造成為政府和企業的關注焦點。然而，受限于回收能力以及高昂的投資成本，廢舊產品的回收前景并不樂觀。盡管中國政府出臺過一系列財政補貼政策（如家電以舊換新、新能源汽車補貼等）用于鼓勵和扶持企業的再制造行為，但補貼對象的界定不太明確，未形成一致結論。文章基于政府的財政補貼政策，研究不同回收企業獲取補貼后，再制造閉環供應鏈的最優決策以及補貼效率問題，旨在回答：政府補貼更能給哪一方提高廢舊品的回收率？補貼誰更能提高供應鏈上各成員的利潤？在政府不同決策目標下的最優單位補貼又是多少？在預算約束下政府應該如何調整財政補貼政策？

目前，閉環供應鏈的相關研究已成為眾多學者爭相探討的話題。一些學者研究了閉環供應鏈中不同回收渠道的選擇問題[1-3]，但他們沒有考慮政府在再制造活動中的作用，也未將社會福利等問題納入考慮范圍。許民利等(2019)[4]則從企業社會責任和廣告效應的角度來分析閉環供應鏈的相關決策，而文章立足于政府補貼的環境下進行探討。

對于政府補貼下的閉環供應鏈研究也已成為當下研究的熱點。馬衛民、趙璋(2012)[5]在以舊換新補貼政策的背景下，從消費者、企業以及閉環供應鏈的規模等角度研究了以舊換新補貼對不同閉環供應鏈模式的影響。Yu 等(2018)[6]以中國2007—2013 年間實施的家電下鄉補貼計劃為研究背景，探討了政府應該補貼制造商還是消費者更能提高消費者福利和企業利潤的問題。Cohen 等(2015)[7]研究了在采用綠色技術的背景下，消費者補貼對制造商反應的影響。陳曉紅等(2016)[8]基于消費者雙重偏好的兩階段模型，對政府補貼下的雙渠道閉環供應鏈決策進行了分析。王玉燕(2012)[9]考慮在政府介入下，分析了雙渠道回收廢舊物資的閉環供應鏈管理模式問題。Mitra&Webster(2008)[10]基于兩階段博弈模型，將政府補貼分別給予制造商、再制造商以及由兩者共享三種情形，分析了與再制造數量成比例的補貼對企業生產和利潤帶來的影響。Hung&Wang(2009)[11]通過案例研究，強調政府補貼政策能有效調動制造企業和回收企業參與回收再制造的積極性。公彥德、王媛(2019)[12]則從物流的角度基于物流外包和自營兩種不同的模式，構建了政府對拆解企業與制造企業同時給予補貼的閉環供應鏈模型。陳軍等(2018)[13]對稅收再補貼下的農產品供應鏈均衡定價與政策效應進行了分析。趙曉敏等(2015)[14]認為政府從制造商處征收產品回收處置費并用于補貼再制造商的調控措施能夠促進再制造產品銷量的提升，從而改善再制造商的盈利狀況。彭志強、宋文權(2016)[15]在新產品與再制品具有差異下研究了政府補貼對閉環供應鏈決策的影響問題。王文賓、鄧雯雯[16]則從政府獎懲機制與稅收補貼機制方面入手，探討了何種機制能使逆向供應鏈產生更強的作用效果。趙敬華、林杰(2017)[17]研究了政府的不同補貼計劃對閉環供應鏈的銷售與回收渠道定價指標均會產生不同的影響。

綜上所知，已有的研究多從政府補貼消費者或制造商的視角，探討閉環供應鏈的優化決策，雖也有涉及多個補貼對象的研究，但只是將政府補貼作為外生參數。文章從持續擴大財政補貼、調整財政補貼結構、提升財政補貼效率三個方面提出了對策建議，研究的創新體現在：一是探討了在政府分別給予不同回收主體補貼的基礎上，回答了補貼誰更優的問題，即從政府層面看，補貼誰能獲得更大的補貼效率；二是在經濟效益、社會福利和社會效益最大化等政府不同決策目標下，分別得出了政府內生的最優單位補貼決策。文章余下內容的安排如下：第二部分為變量選取與基本假設；第三部分為閉環供應鏈決策模型的構建于求解；第四部分為不同情形下的最優決策比較分析；第五部分為政府補貼零售商下的最優補貼效率分析；第六章為數值模擬分析；最后給出了政策建議。

二、變量選取與基本假設

1.變量選取

文章構建模型選取的變量說明如表1 所示。

表1 變量含義

2.基本假設

第一，假設新產品（包括制造商用廢舊品生產的再制造品和用原材料生產的產品）的市場需求為D(p)=α-p，其中α表示市場價格p=0 時的潛在需求[18]；

第二，制造商用原材料生產產品的單位成本大于用廢舊品生產產品的單位成本，即cm＞cr，令Δ=cm-cr，Δ 則為制造商用廢舊品生產再制造品獲得的成本節約；

第三，為保證制造商用廢舊品生產產品有利可圖，則存在cm-cr-b≥0，即Δ≥b；

第四，假設I=kτ2為回收企業回收廢舊物資的投資成本，其中k≥0 為回收廢舊物資的難度系數；

第五，再制造品與用原材料生產的產品同質，即兩者之間的價格和質量無差異；

第六，由于再制造品的價格和新產品一樣，而生產成本低于新產品，因此制造商優先使用回收的廢舊品投入生產，當回收的廢舊品不足以滿足需求時，再用原材料進行生產；

第七，假設所有供應鏈成員共享信息，且決策僅考慮單周期。

三、財政補貼下的閉環供應鏈決策模型

按回收主體的不同，分別將政府補貼給予制造商、零售商和第三方回收商，并運用Stackelberg 博弈方法，分析閉環供應鏈的最優決策，每一種情形都由制造商充當博弈的領導者，零售商和第三方回收商則為跟隨者。

1.補貼制造商（M 模型）

在M模型中，制造商回收廢舊物資，并享受政府給予的補貼。制造商首先決定最優的產品批發價格w 及最優回收率τ，零售商在制造商給出的信息下決定最優的產品銷售價格p。M模型下的閉環供應鏈結構如圖1 所示。

圖1 M 模型下的閉環供應鏈結構

當回收率為τ時，制造商用新原材料和回收的廢舊品生產新產品的總成本分別為cm(1-τ)D(p)，crτD(p)；制造商回收廢舊品的總可變成本為cτD(p)；政府補貼給制造商實施廢舊品回收的總額度則為sτD(p)。據此可得：

制造商的決策目標為：

其中，wD(p)表示制造商將新產品批發給零售商而獲得的總收益，tD(p)為制造商繳納給稅務機關的總的環境稅。

零售商的決策目標為：

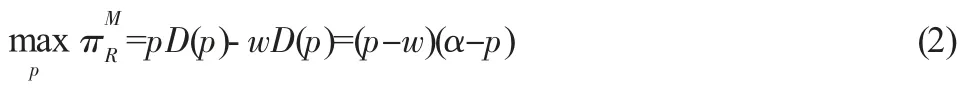
其中，pD(p)表示零售商將新產品銷售給消費者而獲得的總收益，wD(p)則為零售商從制造商處采購新產品付出的總成本。

用逆向歸納法求解，可得如下均衡解：

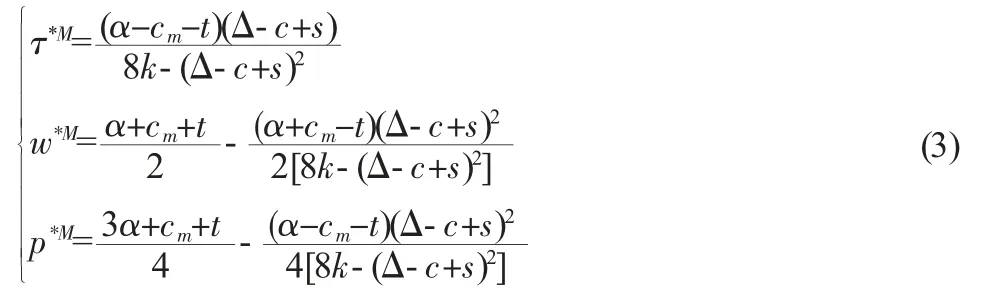
將式(3)各變量分別代入式(1)和式(2)中，得到制造商和零售商的利潤分別為：

2.補貼零售商（R 模型）

在R 模型中，由零售商回收廢舊物資，并享受政府給予的補貼。制造商首先決定最優的產品批發價格w及廢舊品轉移價格b（即零售商將收購回的廢舊品轉售給制造商的單位價格，是制造商的決策變量），零售商再在制造商給出的決策下決定最優的產品銷售價格p及回收率τ。R 模型下的閉環供應鏈結構如圖2所示。

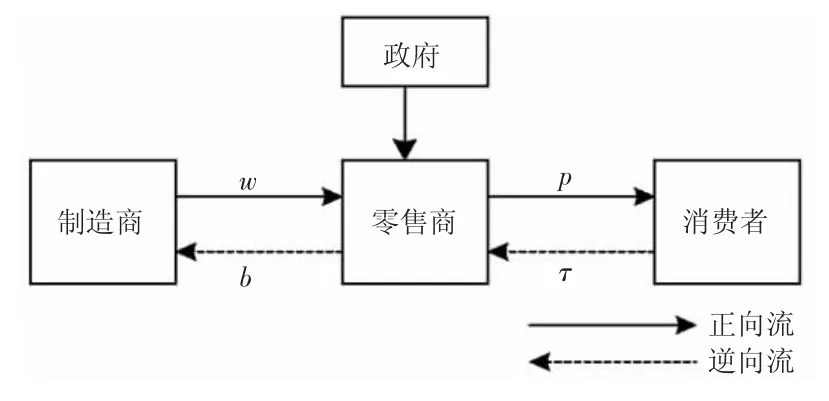
圖2 R 模型下的閉環供應鏈結構

制造商的決策目標為最大化其利潤，即：

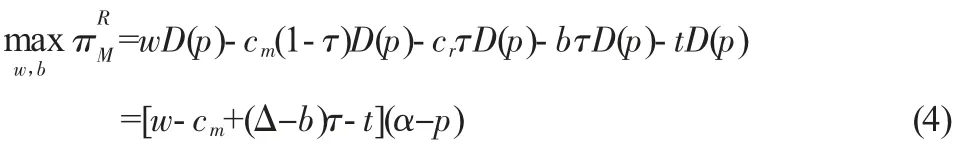
其中，wD(p)表示制造商將新產品批發給零售商而獲得的總收益，cm(1-τ)D(p)與crτD(p)分別表示制造商用新原材料和回收的廢舊品生產新產品的總成本，bτD(p)為制造商從零售商處回購廢舊品付出的總成本，tD(p)則為制造商給稅務機關繳納的總的環境稅。

零售商的決策目標為：

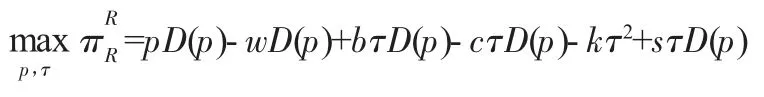
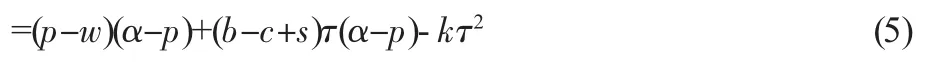
其中，pD(p)表示零售商將新產品銷售給消費者而獲得的總收益，wD(p)則為零售商從制造商處采購新產品付出的總成本，bτD(p)為零售商將回收的廢舊品轉售給制造商而獲得的總收益，cτD(p)與kτ2則分別表示零售商回收廢舊品付出的總可變成本和總投資成本，sτD(p)為政府給予零售商實施廢舊品回收的總補貼額度。

用逆向歸納法求解：由于零售商的目標函數分別是關于p和τ 的凹函數，因此對式(5)分別求p和τ 的一階導數，令其等于零，得：pR=[α+w-(b-c+s)τ]/2，τR=[(α-p)(b-c+s)]/2k，分別將求得的pR和τR代入式(4)中，則制造商的利潤函數變為：

對于任意給定的b，制造商的目標函數是關于w的凹函數，對式(6)求w的一階導數并令其等于零，得：

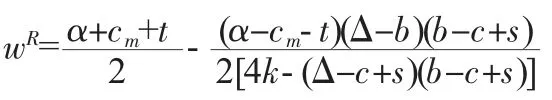
將求得的wR代入制造商的目標函數可得制造商的利潤如下：

命題1：制造商的利潤函數隨著轉移價格b的增加而增加，因此，制造商為最大化自身利潤，會將轉移價格b設置到其上限，即b=Δ。

因此，R 模型下的最優批發價、零售價及回收率分別如下：

相應的制造商、零售商和系統總利潤分別如下：

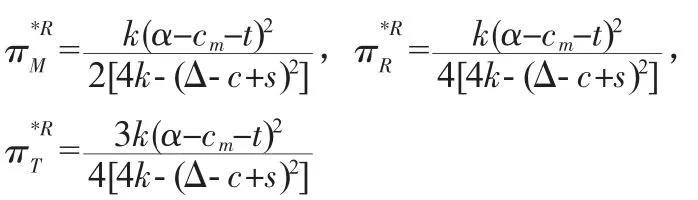
3.補貼第三方回收商（3P 模型）

在3P 模型中，第三方回收商回收廢舊物資，并享受政府給予的補貼。制造商首先決定最優的產品批發價格w及廢舊品轉移價格b（即第三方回收商將回收的廢舊品轉售給制造商的單位價格，是制造商的決策變量），零售商和第三方回收商在制造商給出的決策下決定最優的產品銷售價格p及回收率τ。3P 模型下的閉環供應鏈結構如圖3 所示。

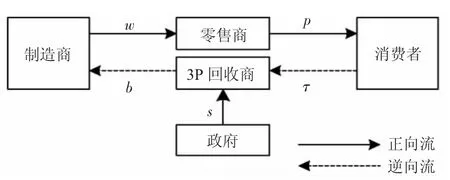
圖3 3P 模型下的閉環供應鏈結構

此時制造商的決策目標為最大化其利潤，即：

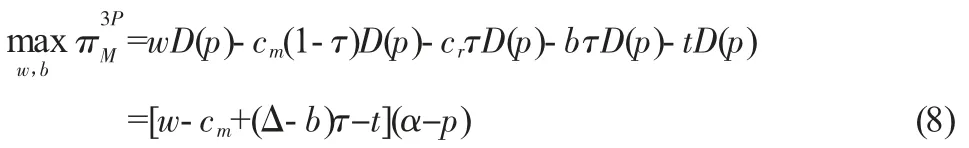
其中，wD(p)表示制造商將新產品批發給零售商而獲得的總收益，cm(1-τ)D(p)與crτD(p)分別表示制造商用新原材料和回收的廢舊品生產新產品的總成本，bτD(p)為制造商從第三方回收商處回購廢舊品付出的總成本，tD(p)則為制造商給稅務機關繳納的總的環境稅。

零售商的決策目標為：

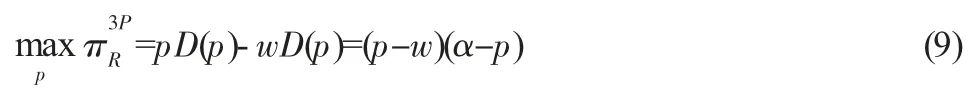
其中，pD(p)表示零售商將新產品銷售給消費者而獲得的總收益，wD(p)則為零售商從制造商處采購新產品付出的總成本。

第三方回收商的決策目標為：

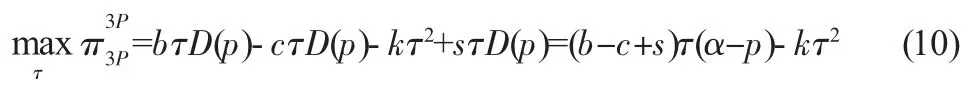
其中，bτD(p)為第三方回收商將回收的廢舊品轉售給制造商而獲得的總收益，cτD(p)與kτ2則分別表示第三方回收商回收廢舊品付出的總可變成本和總投資成本，sτD(p)為政府給予第三方回收商實施廢舊品回收的總補貼額度。

用逆向歸納法求解，首先求得第三方回收商決定的回收率以及零售商決定的銷售價格分別為：τ3P=(α-p)(b-c+s)/(2k)，p3P=(α+w)/2；將求得的τ3P和p3P代入式(8)中，則制造商的目標函數可改寫為：

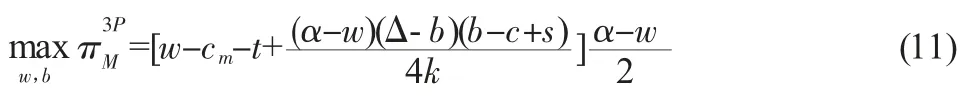
對于任意給定的b，制造商的目標函數是關于w的凹函數，對式(11)求w的一階導數，并令其等于零，得：

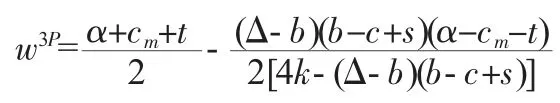
將求得的w3P代入式(11)中，可得制造商的利潤如下：

命題2：制造商的利潤函數在轉移價格b=(Δ+c-s)/2 處取得最大值。

因此，3P 模型下的最優批發價、零售價及回收率分別如下：

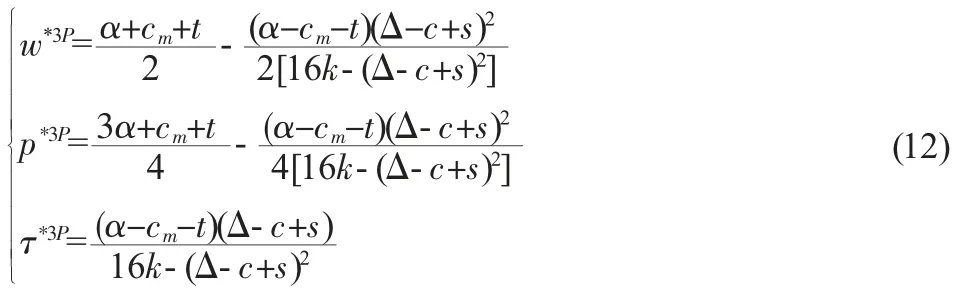
相應的制造商、零售商、第三方回收商利潤分別如下：

四、財政補貼下三種閉環供應鏈模型的比較分析

首先界定一下參數的范圍，由于回收率τ∈(0，1)，因此有下述關系成立：

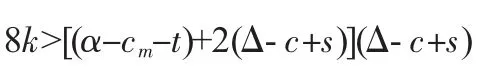
通過比較分析表2 的結果，可得到如下命題：

表2 政府不同補貼對象下的閉環供應鏈模型比較

命題3：τ*R＞τ*M＞τ*3P且

命題3 表明政府將補貼發放給零售商可以得到更大的回收率，而補貼給第三方回收商得到的回收率最低。這是因為：3P模型中的成本節約和邊際投資收益(b*3P-c+s)＜(Δ-c+s)低于M 模型，從而使得3P 模型下的產品回收率低于M模型下的回收率；零售商可以通過決定產品銷售價格來影響市場規模，且回收再制造下的成本節約最終會反映在產品的銷售價格上，因此，M模型下的產品回收率低于R 模型下的回收率。此外，不管政府補貼給哪一方，其回收率均與政府補貼成正比。

命題4：p*R＞p*M＞p*3P且＜0，因此，D*R＞D*M＞D*3P且＞0。

命題4 表明，R 模型下的產品銷售價格最低，而3P 模型下的產品銷售價格最高。這是因為在政府補貼下，零售商可以通過其定價決策直接反映最終需求的單位成本節約，而制造商則是通過降低批發價格來間接增加產品需求，第三方僅能從回收再制造獲益，因此，R 模型下的產品銷售價格降幅最大，與之相對應的產品需求也最大。此外，不管政府補貼給哪一方，產品銷售價格均與政府補貼成反比，而相應的產品需求則均與政府補貼成正比。

命題5 表明，在不同政府補貼對象下，就制造商和零售商的利潤而言，其排序均為R 模型＞M 模型＞3P 模型，相應的供應鏈系統總利潤也呈現出R 模型最大、3P 模型最小的排序；此外，不管政府補貼給哪一方，供應鏈系統總利潤均與政府補貼成正比。

五、不同目標下的最優補貼決策

經過比較分析，發現政府補貼給零售商能使廢舊品的回收率、新產品的銷售價以及閉環供應鏈上的系統總利潤達到最優，即補貼零售商能達到更好的效率，因此以補貼零售商為研究對象，探討政府在追求不同目標下的最優補貼決策方案。

1.政府目標為追求經濟效益最大化

這里的經濟效益指的是供應鏈上的系統總利潤與補貼成本之差。閉環供應鏈上的系統總利潤為制造商和零售商利潤之和；而補貼成本則為政府對零售商實施補貼的額度，此時政府的目標函數為：

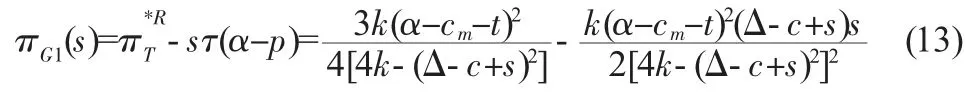
求得政府對零售商實施的最優單位補貼為：

2.政府目標為追求社會福利最大化

這里的社會福利不僅包括前面提到的經濟效益，還包括政府關注的消費者剩余。此時，政府的目標函數為：

其中，(α-p)2/2 表示消費者剩余。求得此時政府對零售商實施的最優單位補貼為：

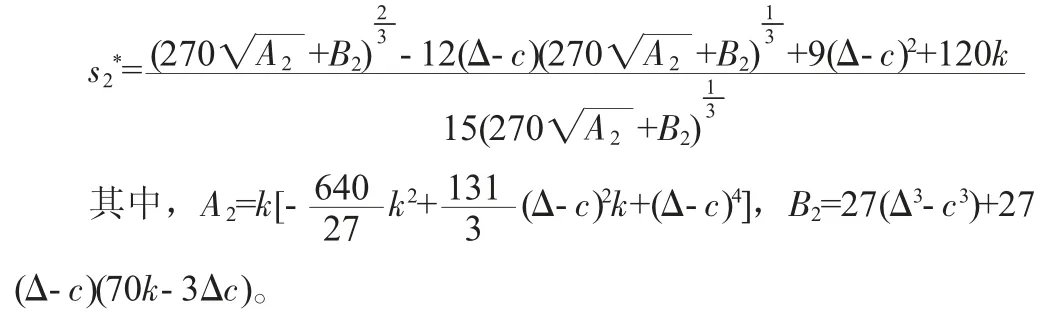
3.政府目標為追求社會效益最大化

這里的社會效益不僅包括整個社會福利，還包括由于進行回收再制造所帶來的環境效益，因此政府的決策目標為社會福利加上環境效益，即：

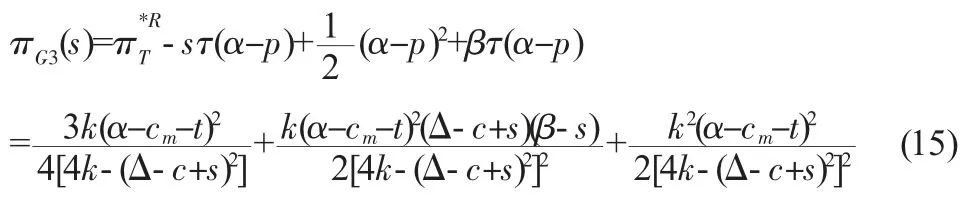
其中，βτ(α-p)為進行回收再制造所帶來的總的環境效益，β 為進行回收再制造帶來的環境效益系數。求得此時政府對零售商實施的最優單位補貼為：

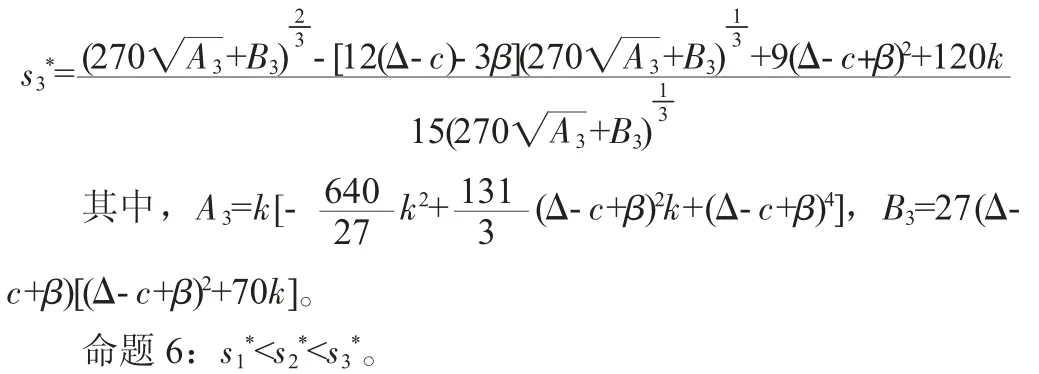
命題6 表明當政府追求的目標所考慮的因素越多（從單純考慮經濟效益到將消費者剩余納入其中，再到將環境效益納入考慮范圍），其所支出的政府最優單位補貼越大。

六、數值模擬分析

設國內某家用電器廢舊物資回收再制造的閉環供應鏈相關參數為：α=100，cm=60，cr=35，Δ=25，c=12，k=400，t=10，β=2。說明政府補貼對各個參數及決策變量的影響，仿真結果見表3。

表3 政府補貼下的閉環供應鏈仿真結果

表3 表明，在不同政府補貼水平下，三種政府補貼模型下的廢舊品回收率均隨著政府補貼的增加而增加，其中R 模型下的回收率增加趨勢更加明顯；在同一政府補貼水平下，總是R模型下的廢舊品回收率＞M 模型＞3P 模型，這一結論與命題3相吻合。

三種政府補貼模型下的產品銷售價格均隨著政府補貼的增加而遞減，且R 模型下的銷售價格降幅最大；在同一政府補貼水平下，總是R 模型下的產品銷售價格＜M模型＜3P 模型，這與命題4 相吻合。由于產品需求是關于銷售價格的線性單調減函數，因此隨著產品銷售價格的降低，其對應的需求會增加，并且R 模型下的產品需求增加幅度最大。

在三種政府補貼模型下，制造商和零售商的利潤均隨著政府補貼的增加而增加，且在R 模型下的增加趨勢更加顯著；在同一政府補貼水平下，制造商和零售商的利潤排序為：R 模型＞M模型＞3P 模型。此外，供應鏈系統總利潤也隨著政府補貼的增加而增加，同樣在R 模型下的增加趨勢更加顯著，在同一政府補貼水平下，閉環供應鏈的系統總利潤呈現出R 模型＞M模型＞3P 模型，這與命題5 相吻合。政府追求的經濟效益、社會福利以及社會效益等不同目標均隨著政府補貼的增加呈現出先增后降的趨勢；在同一政府補貼水平下，政府考慮的因素越多其目標就越高。此外，當政府考慮的因素越多（從單純考慮經濟因素到增加消費者剩余，再到增加環境效益），其給出的最優補貼也越大，即經濟效益最大化下的最優補貼＜社會福利最大化下的最優補貼＜社會效益最大化下的最優補貼，這與命題6相吻合。

七、研究結論與政策建議

文章通過構建Stackelberg 博弈模型，研究了財政補貼制造商、供應商和回收商的效率，并以補貼零售商為例計算了財政補貼的社會福利效應。研究結果表明，第一，不管政府補貼給哪一方，三種模型下的產品回收率均隨著政府補貼的增加而增加，其中政府補貼給零售商可以帶來更高的回收率；第二，三種政府補貼模型下的產品銷售價格均隨著政府補貼的增加而減少，且政府補貼給零售商所帶來的產品銷售價格降幅最大；第三，三種政府補貼模型下的制造商利潤、零售商利潤和系統總利潤均隨著政府補貼的增加而增加，其中政府補貼給零售商可以為制造商、零售商和供應鏈系統帶來更高的利潤，這有效提高了制造商和零售商回收廢舊物資的積極性；當政府追求的目標越高，其所支出的最優補貼則越大。最后，基于經濟效益最大化、社會福利最大化以及社會效益最大化下的最優補貼可為政府決策提供參考意見。

根據研究結論，文章認為政府在補貼廢舊產品回收時，需要注意以下兩個方面：

第一，繼續增加財政補貼，調整財政補貼結構。研究分析表明，不論在何種模型之下，隨著政府財政補貼的增加，廢舊產品的回收率會提高、產品銷售價格會下降、各方利潤會增多，因此，繼續增加財政補貼仍然是提高整個社會福利的重要手段。一方面，提高財政補貼標準。以對環境污染較大的廢舊電子電器產品為例，電視機、電冰箱、洗衣機、微型計算機的補貼標準由2012 年的85 元/臺、80 元/臺、35 元/臺、85 元/臺調低至2021 年的42.5 元/臺、55 元/臺、27.5 元/臺、45 元/臺，財政補貼標準下降會阻礙其提升廢舊產品回收的效果，所以，亟需提高財政補貼標準，提升廠商回收廢舊產品的積極性。另一方面，降低財政補貼門檻。在實踐中，政府對廢舊產品的補貼往往設置了很多限制，例如對回收14 寸以下的廢舊電視機和容量小于50 升的電冰箱等不予補貼，這不僅會降低回收廢舊產品的積極性，還會對環境產生很大的負面影響，所以，須降低財政補貼的門檻，減少廢舊產品對環境污染的潛在危害。此外，文章的分析還表明，政府補貼給零售商能達到最高的回收率、最低的市場價格、最大的企業總利潤，因此，政府在制定補貼政策時，在持續加大財政補貼的基礎上，應將補貼環節適當后移，更多傾向于補貼零售商。

第二，提高財政補貼績效。文章的分析認為，政府目標中，最優補貼成本的大小排序依次是社會效益最大化、社會福利最大化、經濟效益最大化，即政府所追求的目標越高，其所付出的成本就越大。在碳達峰、碳中和背景下，環境保護與綠色供應鏈觀念深入人心，政府應致力于追求環境保護的社會效益最大化目標。然而，地方財政收支缺口較大，財政壓力逐年陡增，用于補貼廢舊產品回收的財政資金自然面臨預算緊約束的問題，因此，將有限的財政資金予以合理配置，發揮其最大效益是政府迫切需要解決的問題。建議加快全過程績效管理的建設和應用以提高財政補貼績效。首先，建立事前績效預評估機制。對于廢舊產品回收的重大項目，要對項目的合理性和可行性開展研究，如果項目可行但不合理，須立即停止；如果項目合理但不可行，須重新研究方案。其次，強化事中績效運行監控。對于已經立項的廢舊產品回收項目，如果發現重大問題，須立即停止撥款和補貼，敦促及時整改，確保績效目標高質量達成。最后，開展事后績效評價。廢舊產品回收項目完成后，可組織三方力量開展評估，發揮專業力量，給出專業意見，強化結果應用。