懸澆拱橋索力設計計算分析

王玲麗、陶鵬飛

（貴州省交通規劃勘察設計研究院有限公司，貴州 貴陽550001）

0 引言

拱橋主拱圈線形為曲線，拱腳支撐處同時受豎向力、水平力作用，水平力既減小了拱橋跨中彎矩，又在拱內產生了軸向壓力，提高了混凝土拱橋的承載力。拱橋跨度和施工方法緊密相關，200～300m 跨度的拱橋主要采用懸臂法施工，斜拉扣掛懸臂澆筑法是通過在交界墩上設置扣塔，利用扣錨索系統拉住拱圈懸臂澆筑節段，待合龍段混凝土澆筑后，逐步對稱拆除扣錨索，再澆筑拱上墊梁、立柱、蓋梁、上部結構、橋面系。

拱圈懸澆過程中，為保證混凝土拉應力不超限，須選擇合適的扣錨索進行拆除，合龍段合龍后，逐步對稱拆除余下全部扣錨索，因此，成橋后拱圈混凝土的受力狀態不能通過調整扣錨索改善拉力，施工過程中扣錨索的初始張拉力對拱橋的受力影響較大。以主跨200m 懸澆拱橋為例，介紹懸澆拱橋扣錨索設計及初始索力的確定過程。

1 工程概況

婭石慶特大橋是貴州省金沙經仁懷至桐梓高速公路上的重要控制性工程，橋位地處烏蒙山與婁山山脈的交匯處，場區為深切“U 形”溝谷地形，溝谷寬約139m，深約115m，河兩岸陡崖前緣均有卸荷裂隙帶，卸荷裂隙走向基本與陡崖平行，垂直豎向發育，延伸較長。 梁基線通過地段的地面高程為865.9～1041.2m，相對高差175.3m。

綜合考慮地形、地質、施工、造價等因素，全橋孔跨布置為：2×30 簡支T 梁+200m（凈跨徑）鋼筋混凝土箱型拱+6×30 先簡支后結構連續預制T 梁，橋梁全長469.2m，全橋立面圖如圖1 所示。

圖1 全橋立面圖

2 扣錨索設計計算

為保證施工過程中混凝土拉應力不超限以及成橋后線形，需對扣錨索及扣錨索的張拉過程進行設計，扣錨索及扣錨索的張拉過程設計包括：扣錨索張拉端位置的設計、扣錨索鋼束根數的設計、各扣錨索張拉拆除順序的設計、扣錨索張拉力的設計。

2.1 扣錨索張拉端位置的設計

根據扣錨索提供更大的豎向力、扣索傾角不小于10、扣塔的高度不至于太高的原則，確定0～16 號扣索在交界墩及扣塔上的張拉端位置，同時為平衡扣索產生的拉力，保證交界墩的穩定，設置與扣索相對應的錨索。扣錨索布置形式有星式布置、扇形布置兩種，星式布置可以提供更大的豎向力，扇形布置方便布置扣錨索。該項目采用星式與扇形組合布置形式，全橋主拱圈共設置17 個節段，金沙岸、桐梓岸分別設置17 對扣錨索，0～6 號扣索采用星式布置，7～16 號扣索采用扇形布置。扣錨索張拉端布置形式如下：0～3 號節段扣錨索在交界墩中部操作平臺的鋼板上，4～6 號節段扣錨索在交界墩蓋梁的錨箱上，7～16 號節段扣錨索在扣塔第一至四層的鋼錨箱上。

2.2 扣錨索鋼束根數設計

扣索主要用于承受懸澆節段重量及施工掛籃重量，根據懸澆節段重量、施工掛籃重量、扣索傾角，初步確定需要的扣索鋼束根數。同時，為平衡扣索產生的水平力，根據錨索傾角，初步確定需要的錨索鋼束根數。待求出索力后，反算出拉索面積及需要的鋼束根數。

2.3 各扣錨索張拉拆除順序的設計、扣錨索張拉力的設計

扣錨索張拉力的設計可參考斜拉橋索力的設計方法，斜拉橋索力優化包括兩大類：恒載索力無約束優化法、有約束優化法，主要有簡支梁法、零位移法、內力（或應力）平衡法、最小彎曲能法、可行域法等。該項目采用最小彎曲能法，將索力優化的目標條件設為施工過程中拱圈混凝土的拉應力不超限，且施工過程中拱圈線形與成橋線形接近，目標狀態先選取最大懸臂狀態下，再根據扣錨索張拉拆除順序確定相應的目標狀態。

最小彎曲能法可采用將主拱圈、交界墩的抗彎剛度縮小10以及將主拱圈、交界墩、扣錨索的截面面積放大10兩種方式，設計中分別采用上述兩種方式計算不拆除扣錨索最大懸臂狀態下的扣錨索的內力，并將求得的結果對比。利用Midas 建立有限元模型，先采用將主拱圈、交界墩的抗彎剛度縮小10，令拉索的初始拉力為零，計算提取扣索內力；另建模型，將主拱圈、交界墩、扣錨索的截面面積放大10，令拉索的初始拉力為零，計算提取扣索內力，以上兩種情況下索內力對比如圖2 所示，通過對比圖發現，縮小主拱圈、交界墩的抗彎剛度后計算出的扣索內力稍微規則一些，而放大主拱圈、交界墩、扣錨索的截面面積后計算出的扣索內力分布非常不規律，因此，該項目運用的最小彎曲能量法，均采用將主拱圈、交界墩的抗彎剛度縮小10；另外，從圖中可以看出K0～K5 的扣索索力值普遍較小，且呈現明顯不規律變化，說明索的布置需要調整。

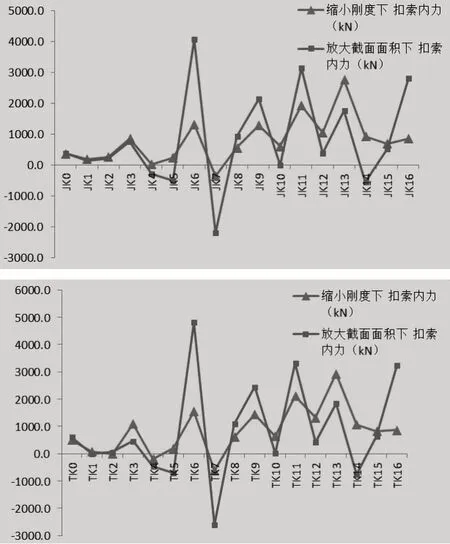
圖2 扣錨索索力對比圖

根據上述分析，將目標狀態設為主拱圈施工至5號節段時0～5 號扣錨索拉住0～5 號主拱圈（狀態一）、最大懸臂狀態下6～16 號扣錨索拉住主拱圈（狀態二），并采用最小彎曲能法分別計算兩種狀態下的扣錨索索力值，發現狀態一下0～5 號扣錨索的索力值均為正值，且沒有突然變小的現象。分別建立0～5號、0～6 號、0～7 號、0～8 號、0～9 號、0～10 號扣錨索拉住主拱圈模型，計算以上各種狀態下的扣錨索索力值，發現0～10 號扣錨索拉住主拱圈時，7 號扣錨索索力值突然變小，因此在張拉10 號扣錨索時，需拆除某個扣錨索。為保證施工安全及主拱圈拉應力不超限，需分批次拆除0～6 號扣錨索，擬定張拉5 號扣錨索時拆除0 號扣錨索，張拉6 號扣錨索時拆除1 號扣錨索，張拉11 號扣錨索時拆除2 號扣錨索，制定扣錨索張拉拆除順序如下：張拉0 號扣錨索—張拉1 號扣錨索—張拉2 號扣錨索—張拉3 號扣錨索—張拉4 號扣錨索—張拉5 號扣錨索、拆除0 號扣錨索—張拉6號扣錨索、拆除1 號扣錨索—張拉7 號扣錨索—張拉8號扣錨索—張拉9 號扣錨索—張拉10 號扣錨索—張拉11 號扣錨索、拆除2 號扣錨索—張拉12 號扣錨索、拆除3 號扣錨索—張拉13 號扣錨索、拆除4 號扣錨索—張拉14 號扣錨索、拆除5 號扣錨索—張拉15 號扣錨索—張拉16 號扣錨索—合龍段合龍后，依次對稱拆除6、16 號扣錨索，再拆除7、15 號扣錨索，依次類推，共5～6 批分級卸載。合龍段合龍時全橋模型如圖3所示。

圖3 合龍段合龍時全橋模型圖

根據擬定的扣錨索張拉拆除順序，利用最小彎曲能法或Midas 的未知荷載系數法，初步確定扣錨索初始拉力。目前扣錨索的張拉方式有兩種，一種是一次張拉到位，施工過程中不再調整索力，另一種是先施加初始拉力，張拉其他節段扣錨索時再調整該索力。因拱圈節段較多，扣錨索數量較多，多次調整索力為施工帶來不便。在200m 左右跨度拱橋中，多采用一次張拉到位，施工過程中不再調整索力的方法，該項目也采用一次張拉到位，施工過程中不調整索力的方法。分別采用上述兩種方法計算扣錨索初始索力。

首先，采用最小彎曲能法計算各狀態下的扣錨索內力值，建立0～5 號、1～5 號、2～6 號、3～11 號、4～12 號、5～13 號、6～14 號、6～16 號扣錨索拉住主拱圈狀態模型，上述各狀態的計算結果中，仍有個別扣錨索內力值為負，或突然變小情況，取各狀態下的內力平均值的最大值作為扣錨索初始拉力。根據施工順序建立含施工階段的模型，將主拱圈、交界墩的抗彎剛度恢復正常后代入前述扣錨索索力，驗算各施工階段主拱圈混凝土的拉應力是否超限。通過計算發現，初始拉力下，大部分施工階段的混凝土最大拉應力超限，需逐個階段調整扣錨索拉力值，比如張拉1 號索力后混凝土最大拉應力超限，即需調整1 號索索力值，直至張拉1號索力后混凝土最大拉應力不超限，再查看張拉2 號索力后混凝土最大拉應力是否超限，如超限即調整2號索索力值，直至張拉2 號索力后混凝土最大拉應力不超限，依此類推，直至合龍段合龍，得到各扣錨索的拉力值。各扣錨索的初始拉力值如圖4 所示。

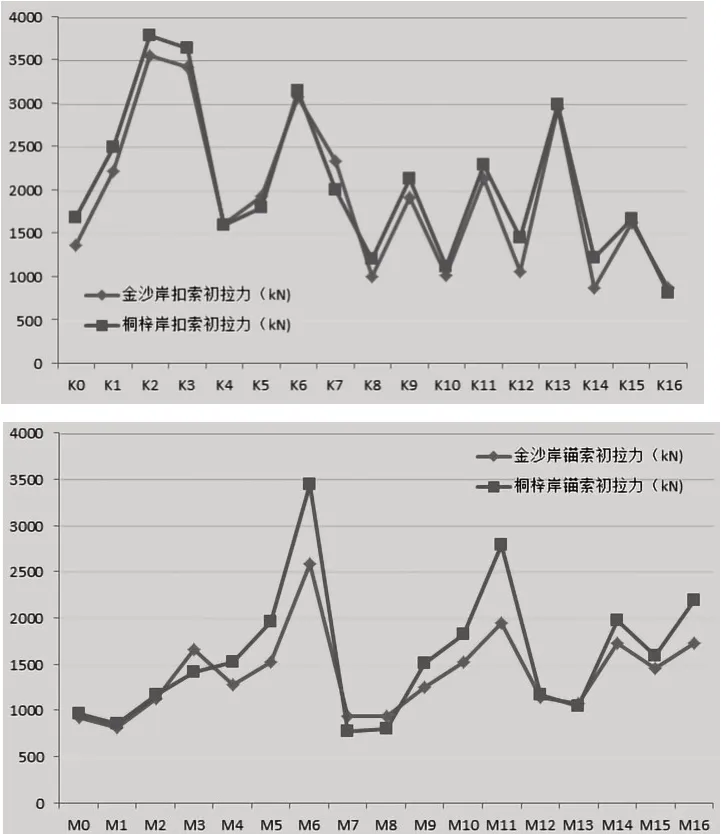
圖4 采用最小彎曲能法計算的扣錨索初始索力圖

為對比，再利用Midas 的未知荷載系數法，按擬定的施工順序建立施工階段模型，將拉索的初拉力設為100kN，以各施工階段下各扣索拉住的箱梁節段的節點位移在±3mm 之間為控制目標，利用程序自帶的未知荷載系數法計算出各扣錨索張拉拆除階段的荷載系數，取各階段荷載系數的最大值與100 的乘積作為扣錨索的初始張拉力。各扣錨索的初始拉力值如圖5 所示。

圖5 采用未知荷載系數法計算的扣錨索初始索力圖

扣錨索張拉過程中主拱圈的壓應力儲備較小，箱底出現拉應力。

3 結論

本文結合主跨200m 懸澆拱橋，介紹了懸澆拱橋扣錨索設計及初始索力的確定過程，并得出如下結論：

第一，懸澆拱橋的扣錨索張拉力設計可參考斜拉索索力的確定方法，但因懸澆拱橋的扣錨索為臨時構件，拱圈合龍后所有扣錨索均需拆除，因此需首先確定扣錨索的張拉拆除順序；

第二，最小彎曲能法計算懸澆拱橋的扣錨索初始索力時，采用縮小剛度的方法比采用放大截面面積法計算的索力均勻；

第三，拱橋懸澆過程中，扣錨索張拉過程中主拱圈的壓應力儲備較小，箱底出現拉應力。