基于Watterson 信道模型的短波信道仿真與實現*

王健 孫 潔

（1.武漢郵電科學研究院 武漢 430074）（2.烽火通信科技股份有限公司 武漢 430205）

1 引言

目前，新型無線電通信系統不斷出現，短波這一古老、傳統的通信方式仍然受到全世界的普遍重視，不僅沒有被淘汰，而且還在不斷地快速發展。因為它有著其他通信系統不具備的優點［1］。評估短波通信系統的性能通常有兩種方法，即理論分析和實驗測量［2］。在理論分析方法中，目前比較常用的有以下幾種短波信道模型：1）Watterson 等提出的高斯散射抽頭延遲線模型［3］；2）Hoffmeyerd 等提出的基于電離層參數的信道模型［4］；3）Giles等提出的基于短波信道沖激響應的直接測量法模型［5］；4）V.E.Gherm等提出的基于散射函數的寬帶短波信道模型［6］等。而Watterson 模型因其復雜度低且能較好地反映短波信道的傳輸特點，在這幾種模型中被廣泛應用并被CCIR推薦［7］。

2 Watterson信道模型

短波信道在時間和頻率上都是不穩定的，但是如果將信道帶寬限制在10kHz以內，信號的傳輸時間足夠短（小于10min），那么大多數信道是相對穩定的［3］。從1965 年開始，經過5 年時間的研究，Watterson 等提出了一種高斯散射抽頭增益延遲線模型來模擬短波信道，簡稱Watterson 信道模型［3］。該模型如圖1所示。

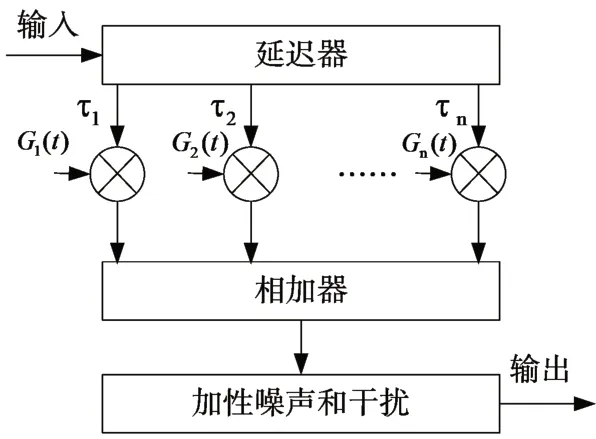
圖1 Watterson信道模型

圖中i是整數，表示第i條抽頭或路徑，τi表示第i條路徑的時延，n是路徑的總數，隨機過程Gi(t)是第i條路徑的抽頭增益函數。輸入信號首先被送入抽頭延時器，每個抽頭可以看作是電離層的一條傳播路徑，通過改變時延τi的值來模擬多徑效應。然后，不同的Gi(t)對延時后的信號的幅度和相位進行調制來模擬多普勒頻移與多普勒頻率擴展。最后延時和調制后的各路信號相加，再加上噪聲和干擾形成輸出信號。

2.1 Watterson信道模型的假設條件

關于抽頭增益函數Gi(t)的統計性說明包含三個假設條件［3］。

1）瑞利衰落假設：假設每一個抽頭增益函數Gi(t)是一個復高斯隨機過程，其幅度服從瑞利分布。根據瑞利分布的概率密度函數，可得到抽頭增益函數Gi(t)的概率密度函數為

這里，Gi(t)的均值為0，幅度服從瑞利分布，相位服從均勻分布。

2）獨立性假設：每個抽頭增益函數Gi(t)都是相互獨立的。因此，任意兩條路徑抽頭增益的聯合概率密度函數就可以表示為

3）高斯功率譜假設：假設抽頭增益函數Gi(t)的功率譜v(f)具有高斯分布的形狀或者可以看成是兩個具有高斯分布形狀的頻率函數的和［5］：

這里F[].表示關于t的傅里葉變換。

這里fa和fb為分量a和b的多普勒頻移，σa和σb為分量a和b的多普勒頻率擴展的因子，Ca和Cb為分量a和b的功率增益。

2.2 Watterson信道模型的傳輸函數

Watterson信道模型的時變頻率響應可表示為

抽頭增益函數Gi(t)反映了高頻信道的時變衰落特性，可以表示為

式中Gia(t)和Gib(t)是兩個相互獨立，各態歷經的復高斯平穩隨機過程，它們是相互獨立的正交分量，均值為0，有相等的均方根值和頻譜。

將Gia(t)定義為實部和虛部的形式：

(0)是Gia(t)的自相關函數在Δt=0 時的值，代表信道輸出信號功率與輸入信號的比值，即功率增益。Gi(t)的自相關函數［8］為

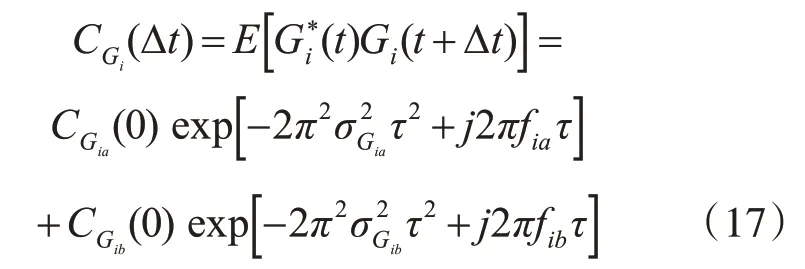
根據維納-辛欽定理，可以求得Gi(t)的功率譜密度［8］為

這里Ci(0)=Cia(0)+Cib(0)，fia和fib為多普勒頻移的值，2σGia和2σGib為多普勒頻率擴展的值。

3 Watterson信道模型的仿真方法

根據以上對Watterson 信道模型的分析，可以設計出如圖2所示的結構框圖［9］來進行仿真。

圖2 Watterson信道模型的結構框圖

Watterson 信道模型的仿真主要分為希爾伯特（Hilbert）濾波器的仿真、多徑效應的仿真、多普勒頻移的仿真、多普勒頻率擴展仿真和噪聲仿真五部分。以下對每種仿真進行說明。

3.1 希爾伯特（Hilbert）濾波器的仿真方法

首先產生一個輸入信號，將該信號一路輸入3kHz的帶通濾波器（BPF），另一路經過希爾伯特變換后再輸入3kHz 的帶通濾波器，這樣就形成初始復信號I+jQ。經希爾伯特變換后，I、Q 兩路信號的幅度不變，相位相差90°。具體的實現方法［10］如下。

1）設計一個通帶帶寬為1500Hz的有限沖擊響應（FIR）低通濾波器（LPF），其通帶帶寬是帶通濾波器的一半。

2）通過轉換式（19）和式（20），將低通濾波器的系數變為帶通濾波器的系數：

式中，hIBP(n)和hQBP(n)是希爾伯特帶通濾波器的系數，hLP(n)為n 階有限沖擊響應低通濾波器的系數，f0為濾波器通帶的中心頻率，T 為采樣周期，N為希爾伯特濾波器的階數。

3.2 多徑效應的仿真方法

設經過3kHz 帶通濾波器和3kHz Hilbert 帶通濾波器之后的信號為S（t），則S(t)=Iin(t)+jQin(t)，Iin(t)=acos(2πf0t+θ)，Qin(t)=asin(2πf0t+θ) 。模擬多徑效應，只需每一路徑設置不同τi的值，這樣每路就產生了不同的時延，由此得到：

3.3 多普勒頻率擴展的仿真方法

多普勒頻率擴展具體的結構框圖［11］如圖3 所示。

圖3 多普勒頻率擴展的仿真結構框圖

設多普勒頻率擴展前的輸入信號為S(t)=Iin(t)+jQin(t)，通過插值濾波器后的信號為N(t)=II(t)+jQQ(t)，將兩個復序列相乘得到：

3.4 多普勒頻移的仿真方法

多普勒頻移仿真框圖［12］如圖4所示。

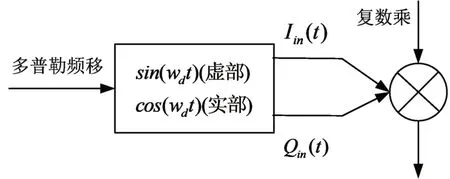
圖4 多普勒頻移的仿真結構框圖

設多普勒頻移為fd，I(t)=cos 2πfdt，Q(t)=sin 2πfdt，多普勒頻率擴展后的信號為S(t)=Iin(t)+jQin(t)，多普勒頻移后的信號為Sfd(t)=Ifd(t)+jQfd(t)。

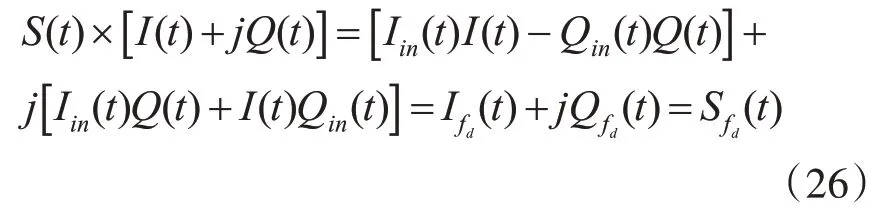
這樣就實現了多普勒頻移，這時，信號的頻率變為f0與fd的和。

3.5 噪聲的仿真方法

信號或者噪聲的均方根可以由式（27）計算［13］：

式中，RMSS表示信號的均方根值，RMSN表示噪聲的均方根值。當信噪比確定后，只需改變RMSN的值，從而達到增加或者減小噪聲的目的。

4 仿真結果

實驗采用CCIR推薦的中緯度地區干擾環境下的短波信道參數［14］，時延為2ms，多普勒頻擴為1Hz，不涉及多普勒頻移的考慮。輸入信號選擇單頻信號x(t)=cos(2πf0t)，f0=400Hz，抽樣頻率fs=3000Hz，信噪比為20dB。輸出信號如圖5所示。

圖5 輸入為單頻信號時的輸出信號時域圖

從輸出信號的時域圖可以看出，信道對輸入信號的相位和幅度產生了隨機性的調制，輸出信號衰落明顯。輸出信號的頻譜圖如圖6所示。

圖6 輸入為單頻信號時的輸出信號頻譜圖

可以看出，輸出信號的頻譜不是δ函數的形式，出現了兩個譜峰并有一定的寬度。這表明輸出信號的頻譜出現了偏移和展寬，產生了多普勒頻移和多普勒頻率擴展的現象，并疊加了白噪聲的頻譜。

在上述基礎上將多普勒頻擴設定為2Hz，輸出信號的時域圖和頻譜圖分別如圖7和圖8所示。

圖7 增加頻擴后的輸出信號時域圖

圖8 增加頻擴后的輸出信號頻譜圖

可以看出輸出信號的衰落和頻譜展寬更大，同時噪聲對輸出信號的影響也更為明顯，清楚地顯示了頻率擴展增加帶來的影響。

5 結語

本文對Watterson 短波信道模型進行了理論推導，并在此基礎上對模型的仿真方法進行了詳細分析。通過Matlab編程，將單頻信號作為輸入信號通過Watterson 信道模型，給出仿真結果，并對結果進行了分析。結果表明，仿真驗證了Watterson 短波信道模型算法的正確性和可行性，該模型可以很好地模擬短波通信信道中存在的多徑延遲、多普勒頻移和多普勒頻率擴展等現象，這對短波通信系統和設備的前期設計具有重要意義。