液壓夯補強路基動力響應現場試驗研究
李 晉,姜 鵬,李天宇,常 德,崔新壯,
(1. 山東交通學院, 山東 濟南 250357;2. 山東大學 土建與水利學院, 山東 濟南 250061;3. 濟南金曰公路工程有限公司,山東 濟南 250101)
0 引言
路基弱碾區或碾壓盲區等填筑位置狹窄,小型夯實設備壓實功較小且施工效率低下,大型壓實機械又不能進場或運行不便,因此這些位置壓實效果普遍較差,極易誘發施工質量問題[1-2]。液壓夯可以實現高強度、高頻率反復施壓,且機動靈活施工作業盲區小,用于上述位置可取得良好壓實效果[3-5],彌補了路基弱碾區及碾壓盲區作業施工質量控制問題的技術空缺,因此采用液壓夯進行路基弱碾區及碾壓盲區的壓實補強施工得到廣泛應用。
明確液壓夯夯實作用下路基動力響應特征有助于優化液壓夯施工工藝、提高路基服役動力穩定性[6],諸多學者們也開展了路基動力響應相關研究。劉本學等[7],馮忠緒等[8]建立了液壓夯-土體相互作用力學模型,并通過室內模型試驗探究了液壓夯用于橋頭臺背的施工效果;馬宗源等[9]借助于離散元數值仿真探討了影響碎石土地基孔隙率的因素,進而用于評價液壓夯動力夯實效果。實際上,在液壓夯沖擊載荷作用下,介質微元體的慣性不應該被忽略,因為慣性力在動力學中同樣能使物體產生變形[10]。研究表明,高應變率、高加載率的動力作用會顯著提高被加載介質的屈服強度與瞬時應力。液壓夯動力夯實作用下,路基土體應力應變關系與靜力下的應力應變關系有很大差異[11-12]。謝永利等[13]探究了液壓夯夯實作用在路橋過渡段填料中的動載傳遞特性,分析了不同路徑中動載豎向傳遞規律。姬猛等[14]通過室內模型試驗分析了液壓夯實法補強橋臺背路基時夯擊能隨著距夯點距離變化的衰減規律,由此可見原位動力響應測試相比于其他研究手段能夠較為真實地反映實際狀況。
針對山東省內一般性粉質黏土路基,本研究采用不同量級的液壓夯開展現場試驗對比研究,分析特定土質下機械-土體相互作用強化機理,探究不同夯擊能作用下粉質黏土填料動應力時空響應與加速度響應峰值的變化規律,以期為液壓夯相關動力壓實研究提供借鑒與參考。
1 動力響應現場試驗
1.1 工程概況
本次試驗路段選擇山東省某改建工程路橋過渡段,施工現場地基分布有可塑、硬塑狀態的濕陷性黃土,對試驗段現場路基填筑所用的素土及灰土(6%)隨機取樣后,依據《公路土工試驗規程》(JTG 3430—2020)進行土工試驗測定并鑒定土質。判定場地內黃土濕陷系數為I級(輕微濕陷),濕陷等級為輕微、中等的一般性粉質黏土,具體土工試驗參數如表1所示。試驗段路基高度為5 m,采用分層填筑施工,松鋪系數為1.3,松鋪厚度為26 cm。
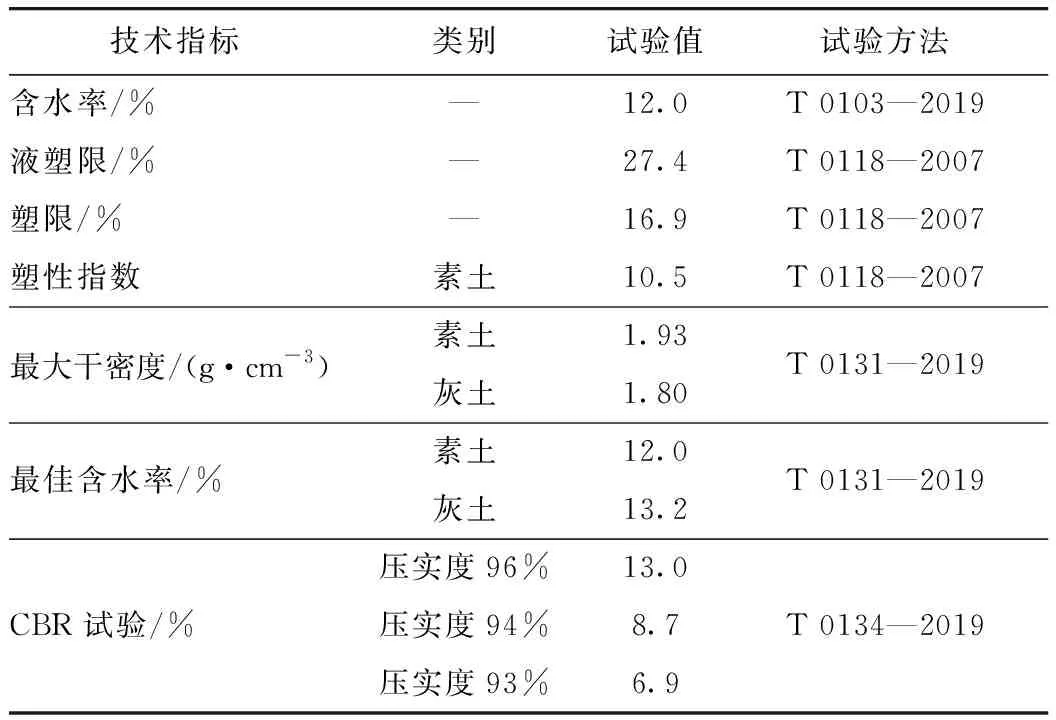
表1 土工試驗結果Tab.1 Geotechnical test result
為了減少道路占地,右側設有支擋結構扶壁式擋墻,其厚度為0.5 m,高6.1 m,扶壁厚度0.5 m。擋墻扶壁間隙屬于路基弱碾區,擬決定采用液壓夯進行壓實補強施工。采用某有限公司生產的3種不同型號的高速液壓夯實機進行擋墻扶壁間隙處壓實補強施工,其具體參數可見表2。
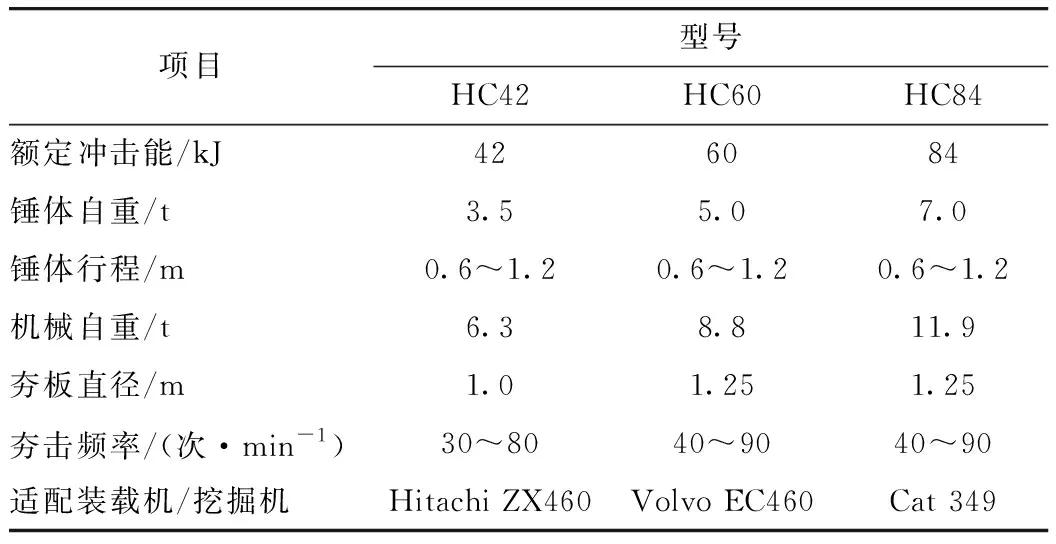
表2 機械技術參數Tab.2 Technical parameters of machinery
1.2 試驗方案
現場試驗擬采用電阻應變式土壓力盒(量程:1.0 MPa,型號:JMYJ-1410,精度:2%F.S)與壓電加速度計(量程:100 g,型號:JMCZ-2091,頻率:1~1 400 Hz)進行一般性粉質黏土路基動態土壓力值與動態加速度監測。采用某技術股份有限公司生產的動態信號測試分析系統及DH5922D采集儀進行動力響應信號的采集與分析。路基分層填筑到規定高度作業面時,采用立方體實心木塊放置于壓實面上采用壓路機壓實直至滿足規定壓實度要求。然后將木塊摳出形成立方體坑洞空間,在坑底滿鋪細砂,水平布設好傳感器后再將細砂灌滿坑洞,將傳感器4壁包圍,然后布置好傳感器導線繼續進行下一層填土壓實。整個施工期間注意導線及傳感器的防損防潮工作。
現場選取兩個擋墻扶壁間隙斷面(A斷面和B斷面),根據傳感器布設方案(如圖1所示)在路基分層填筑施工期間進行傳感器埋設。分層填筑路基頂面施工完畢后,經檢測壓實度為98%,擋墻扶壁間隙處壓實度為96%,含水率為12.0%,可見與正常作業區相比,路基弱碾區壓實質量較差。填筑壓實完畢后,為防止路基土含水率變化,立即分別采用不同型號液壓夯機開展路基弱碾區壓實補強:在兩個斷面規定夯點處采用3.5 t液壓夯各進行6次滿夯擊實,在此基礎上在A斷面夯點處采用7.0 t液壓夯進行6次滿夯擊實,在B斷面夯點處采用5.0 t液壓夯進行6次滿夯擊實,夯實作業的同時數據采集工作同步進行。試驗完畢后,切斷導線,永久滯留傳感器于路基內部。
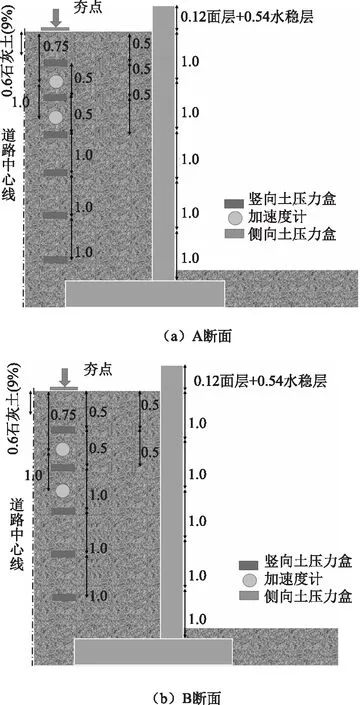
圖1 道路橫斷面傳感器布設示意圖Fig.1 Schematic diagram of layout of sensors in road cross-section
2 動態響應分析與討論
2.1 土體動應力空間響應規律
由試驗數據可知,隨著夯擊次數的增加,土體內任意處應力峰值均是先增大后趨于平穩。這是由于土體受到夯實作用,整體剛度逐漸變大后趨于穩定。取夯點豎直方向上不同深度位置處的平均應力峰值,作出應力響應隨深度變化如圖2所示。

圖2 不同夯實作用下應力響應縱向變化曲線Fig.2 Longitudinal variation curves of stress response under different compaction actions
如圖2可知,在3.5 t液壓夯、5.0 t液壓夯與7.0 t液壓夯夯實作用下,從夯點以下0.5 m到1.0 m 深度處所測得應力峰值分別損失了62.75%,54.56%和50.59%。3.5 t液壓夯在夯點以下1.8 m深度處應力衰減到0.25 MPa以下,而衰減至同樣應力值以下,5.0 t液壓夯的作用深度可達夯點以下2.4 m,而7.0 t液壓夯的作用深度可達夯點以下4.0 m。可見夯擊能越大,應力波影響深度越廣。同時可以注意到與5.0 t液壓夯、7.0 t液壓夯夯實效果相比,3.5 t液壓夯夯實作用下路基土體不僅應力響應相對較小,且在土壤黏性阻尼和幾何阻尼影響下,路基土體應力耗散較快;而在5.0 t液壓夯、7.0 t液壓夯夯實作用下,由克服土體阻尼而造成的夯擊能衰減量相比于3.5 t液壓夯的較少[15]。
由試驗方案可知,除了豎直方向布設了動態土壓力盒,還在路基上部位置,承壓面朝向夯點的水平方向上豎直埋設了動態土壓力盒以監測動態側向土壓力。由豎直土壓力σv可計算得側向土壓力σh,如式(1)所示,不同深度處實測水平向的應力響應如圖4~圖5所示。
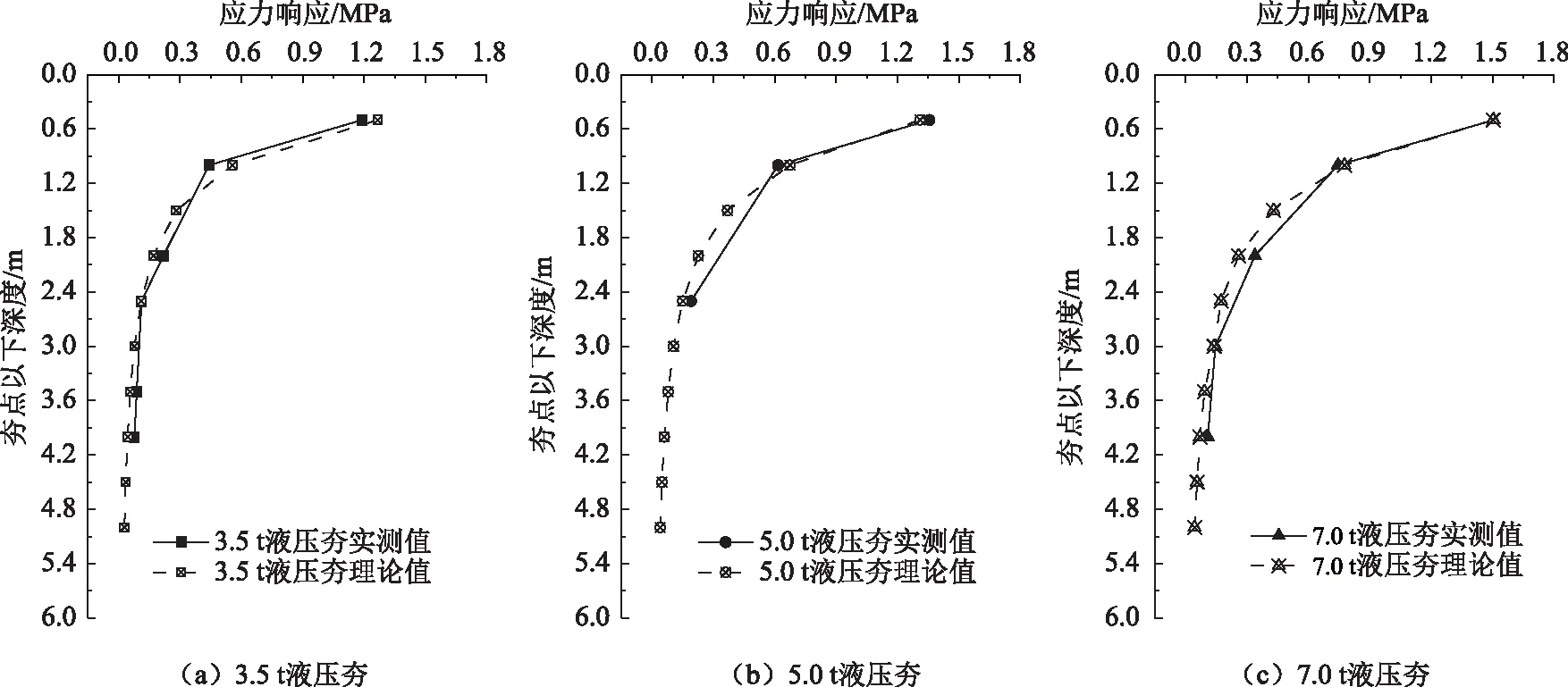
圖5 不同夯實作用下的應力響應曲線Fig.5 Stress response curves under different compaction actions
σh=K0σv=λσv/(1-λ),
(1)
式中,K0為側向土壓力系數;λ為土的泊松比。
圖3(a)所示的是夯點以下0.5 m深度處水平方向上土體應力情況,應力在0.5 m范圍內衰減較慢,超過0.5 m范圍外應力迅速衰減。3.5 t液壓夯、5.0 t液壓夯與7.0 t液壓夯夯實作用下,水平向0.5 m 處應力峰值分別損失了18.28%,12.21%和1.93%,水平向1.0 m處,應力峰值分別損失了82.58%,77.37%和72.16%。圖3(b)所示的是夯點以下1.0 m深度處水平方向上土體應力情況,3.5 t 液壓夯與7.0 t液壓夯夯實作用下,水平向0.5 m 處應力分別損失了8.84%,32.39%,在水平向1.0 m處,應力分別損失了23.97%和53.62%。綜合圖3可知水平方向上,夯擊能越大,應力衰減幅度越大。
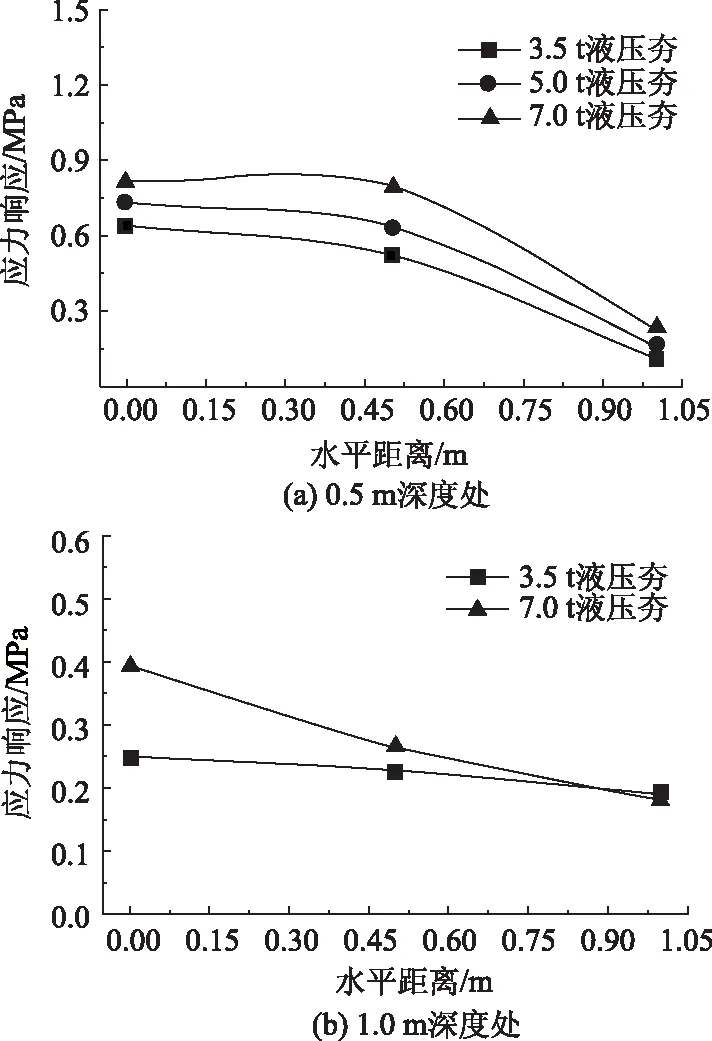
圖3 不同深度處應力響應橫向變化曲線Fig.3 Lateral variation curves of stress response at different depths
2.2 豎向土體動應力解析
基于熱力學領域來看,液壓夯動力沖擊加載的過程屬于絕熱過程,夯實作用使路基表層土體產生了一部分塑性變形,即液壓系統將夯錘抬高產生的重力勢能,在夯錘-土體相關作用中轉化成了路基土體的沖擊壓縮能和塑性變形能[16]。因此學者們多將夯錘-土體相互作用過程看作是動力學中的非完全彈性碰撞[17],但考慮實際工況中不同的參振土體性質與不同的夯錘技術參數,因此,基于本試驗工況,擬提出一種作用于一般粉質黏土的液壓夯動力補強應力解析模型。
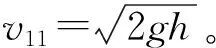
m1v11+m2v21=m1v12+m2v22,
(2)
式中,m1為夯錘質量;m2為參振土體質量。
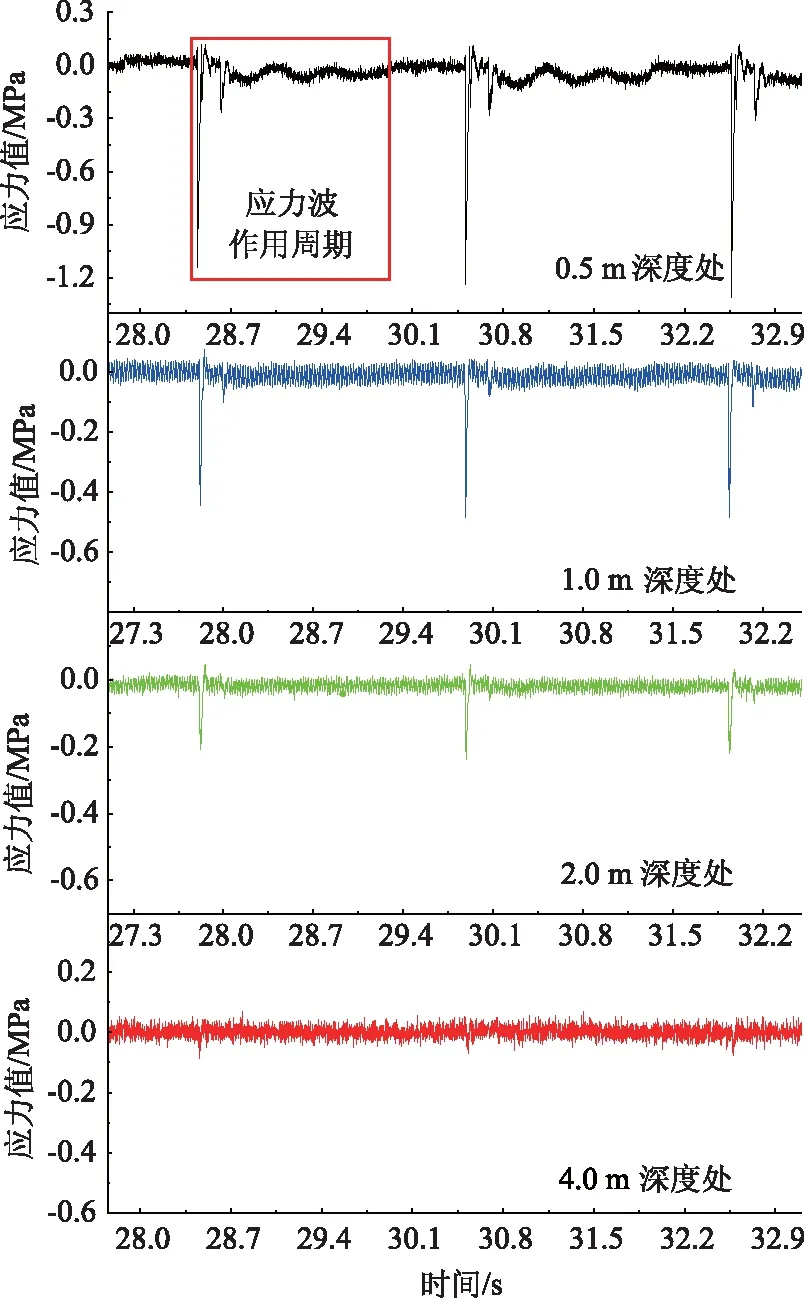
定義一個恢復系數k=(v22-v12)/(v21-v11),可體現土體-夯錘相互作用過程中的能量消耗。土體-夯錘相互作用過程視為完全非彈性碰撞時k=0;土體-夯錘相互作用過程視為完全彈性碰撞時k=1;而當0 (3) 恢復系數k與參振土體性質有很大關聯,假設參振土體均質且為素土,此時由前文土工試驗檢測可知此時土體含水率為12.0%,為最佳含水率。由現場夯點處所測的壓實度為96%可知此時土體密度為2.075 g/cm。本試驗中夯擊6次后土體已經趨向于密實狀態,在此基礎上取k=0.80,取錘體行程的1.72倍的圓柱求得體積后計算參振土體的質量m2。土體-夯錘相互作用瞬間完成后,錘體給土體產生一個速度v22,進而實現對土體的夯實。考慮將地基簡化成圖4所示的阻尼彈簧體系,建立運動方程如式(4)所示。 圖4 非完全彈性碰撞半空間夯實模型Fig.4 Incomplete elastic collision half-space compaction model (4) (5) 相應于最大加速度的時tα: (6) 將夯錘底面壓力視為均勻分布,則此時應力峰值σdmax為: (7) 不同量級液壓夯作用于土體表面產生的應力峰值σdmax通過前文相關機械技術參數與土體參數可計算而得,然后借助于豎直集中荷載作用下的附加應力解析解(Boussinesq解),可計算圓形均布荷載作用下土體內豎直方向上任一點z深度處的附加應力為: (8) 由此可得如圖5所示的夯點正下方應力響應理論值變化情況。 通過圖5可見不同深度處解析模型所得的計算值與實測值基本一致,表明將機械-土體相互作用視為非完全彈性碰撞的基礎上,取恢復系數k為0.8,參振土體為最佳含水率下的一般粉質黏土土質,參振土體體積取底面與錘體底面積一致,高為錘體行程的1.72倍的圓柱體,所得計算值與現場實測值相符程度較高,該參數取值有助于為一般粉質黏土路基液壓夯補強應力計算提供參考。 固體靜力學中往往忽略物體介質慣性導致的可變形性,單純基于靜力平衡狀態計算物體的受力與變形。而介質微元體的慣性在動力學中不應該被忽略,若動力加載時間遠遠小于被加載介質中應力波傳遞時間,此時應力波傳播與相互作用效應不應該被忽略。作出如圖6所示,3.5 t液壓夯作用下夯點豎直方向上土體應力時程曲線。 圖6 不同深度處應力時程曲線Fig.6 Time history curves of stress at different depths 圖6描述了夯點以下不同深度處應力時程曲線。可以看到路基表層土體中應力波呈現出較為劇烈的沖擊特征,由于土體本身的慣性使得應力波又出現了一個較小的波峰,隨即受到應力波的傳播與相互作用效應,土體應力值震蕩波動直至消散。而在路基深層土體中,應力波呈現為彈性振動特征,彈性波動一下,動應力立即恢復歸0狀態。路基表層(0.5 m深度處)在3.5 t液壓夯作用下應力波的加載周期為5 ms,而路基深層(4.0 m深度處)的應力波的加載周期為9 ms。 計算3種液壓夯夯擊作用下應力值波動到恢復歸0狀態(應力波作用周期)的時長。通過對比時間差均值可知,夯點以下0.5 m深度處,3.5 t,5.0 t 和7.0 t這3種液壓夯的應力波作用周期分別為1.466 s,2.223 s和2.902 s。由此可見沖擊能越大,應力波作用周期越長。 液壓夯夯實作用會使土體介質微元體瞬間產生明顯加速度,土體的運動和變形也會受到加速度所引起的慣性力影響,短時間內的動力加載過程中會產生幅值變化較大的動應力集中,進而產生特殊的局部破壞效應[18]。由于路基分層填筑施工過程中損壞了部分加速度計,僅以3.5 t和5.0 t液壓夯為例,作出加速度峰值隨著土體深度的變化情況如圖7所示。 圖7 加速度響應隨著深度的變化Fig.7 Acceleration response varying with depth 由圖7可以看到,在3.5 t液壓夯作用下,夯點以下0.75 m深度處加速度峰值為2.238 m/s2,夯點以下1.25 m深度處僅為0.464 m/s2,土體加速度響應衰減了79.27%。而在5.0 t液壓夯作用下,夯點以下0.75 m深度處加速度峰值為2.786 m/s2,夯點以下1.25 m深度處為0.899 m/s2,土體加速度響應整體衰減了67.73%。由此可見豎向方向上加速度與應力衰減情況相同,沖擊能越大,同一深度處土體加速度響應衰減幅度越小。 進一步地,圖8所示為5.0 t液壓夯夯實作用下土體加速度響應時程曲線。夯擊加載土體產生正向加速度,錘體重力勢能轉化為土體動能。由加速度時程曲線形態可知,錘體-土體相互作用瞬間,夯點以下0.75 m深處土體振動速度先急速增加對應錘體夯擊作用時段,隨后速度緩慢增加至最大值對應夯擊作用完成之后,此深度處的土體表現出較多的塑性狀態,直接產生不可恢復的塑性形變。而由1.25 m 深處加速度值變化情況可知,土體振動速度衰減為0之后又反向加速,說明夯擊作用完成之后,相較于0.75 m深處,1.25 m深處土體表現較多的彈性狀態,大部分土體形變可恢復。 圖8 加速度時程曲線Fig.8 Acceleration time history curves 通過開展本次液壓夯夯實粉質黏土動力響應現場試驗研究,得到以下結論: (1)夯擊能越大,路基土體中應力豎直方向上傳播時損耗越小,應力波影響深度越廣。夯點正下方0.5 m深度處,水平方向上應力衰減幅度先慢后快,夯點正下方1.0 m深度處的水平方向上,隨距離增大衰減幅度增大。總體水平方向上夯擊能越大,應力衰減幅度越大。 (2)將機械-土體相互作用視為非完全彈性碰撞的基礎上,取恢復系數k為0.8,參振土體為最佳含水率下的一般粉質黏土土質,參振土體質量取底面與錘體底面積一致、高為錘體行程的1.72倍的圓柱體,所得計算值與現場實測值相符程度較高。 (3)路基表層土體慣性會使應力波產生第2個波峰,隨后應力值在應力波的傳播與相互作用效應下發生震蕩直至應力消散歸0,而在路基深層土體處,動力夯實作用下表現為彈性振動特征。沖擊能越大,同一深度處應力波作用周期越長。 (4)沖擊能越大,應力波傳遞到夯點以下同一深度處土體加速度響應衰減幅度越小。由加速度時程曲線形態可知,夯點以下0.75 m深處土體表現出較多的塑性狀態,1.25 m深處土體表現較多的彈性狀態。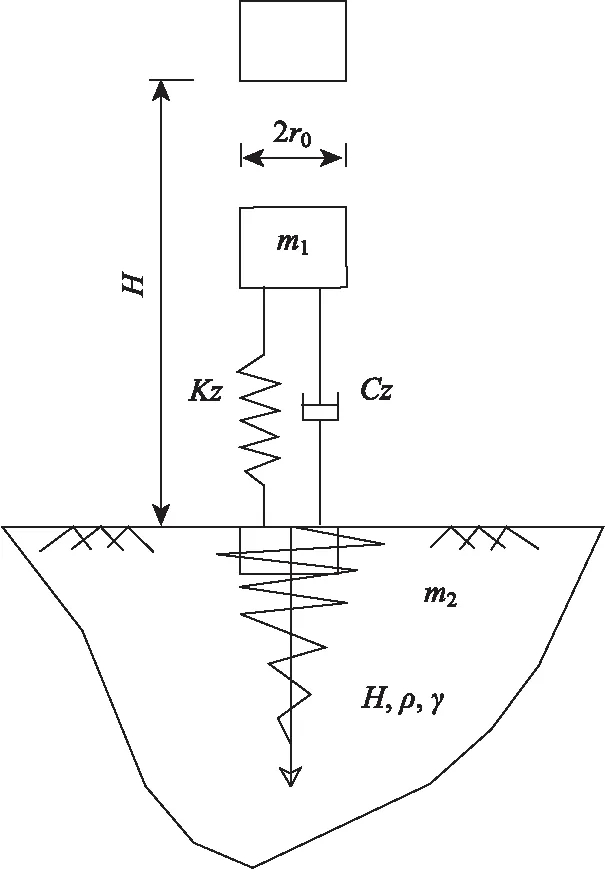
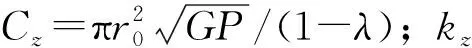
2.3 豎向土體應力時程響應規律
2.4 土體加速度響應規律


3 結論

