黃渤海風浪模擬波高極值在預報服務中的應用
孫倩倩 王 迪 孫顏薇
(山東省威海市氣象局,山東 威海 264200)
1 概述
黃渤海是山東半島航線的主要分布區域,也是專業氣象服務的重要部分。此區域中來往船只較多,因大風引起的災害性海浪會給船舶交通運輸造成巨大的經濟損失和人員傷亡。同時,對于船舶航行停泊和裝卸作業情況,需要對未來一段時間的波浪參數有確切的掌握,才能保證沿海作業的安全穩定運行,而波高極值是波浪參數中最為重要的資料。
目前獲得一定區域內長期波浪數據的方法有很多,除了直接使用NOAA 浮標測量數據的方法外,還可以通過觀測船、衛星高度計、根據風場數據模擬方法。其中,利用波浪模型再現歷史波高這種研究方法在波候分析研究中應用廣泛,可以得到任何有風場數據的水域內連續長期的波高數據,比較主流的模型有WAMC4、WW3、SWAN,根據前人的研究可見,WAMC4 和WW3 模型多用于計算深水情況,而SWAN對于近岸波浪的模擬較好。[1]
黃渤海地區現有的測站多位于沿岸,不能完全表示出整個黃渤海海域地區的長期波浪分布情況,因此采用第三代近岸波浪模型SWAN 模擬追算長期波浪,趙嘉靜等人通過對比評選發現,在中國海域地區,使用歐洲天氣預報中心(ECMWF)風場模擬的極端波情況更接近真實值,因此本文SWAN 模擬的風場來源也使用了ECMWF 風場。
本文的研究目的在于,通過ECMWF 風場數據,利用SWAN 數值模型,實現黃渤海海域波高的模擬再現,并與現有海岸上實測波高的驗證,論述黃渤海海域根據實時或者預報風場資料進行波高預測的可行性。最后根據波高模擬結果,利用Gumbel 型分布函數Person Ⅲ型分布函數來進行極端波高的預測預報,為后續與波高有關的工程建設、民商互動和船舶作業提供參考決策。
2 波高模擬及驗證
2.1 模型與驗證
為了預測黃渤海海域波高情況,利用歐洲天氣預報中心(ECMWF)風場數據驅動模型,該中心于1979年首次做出了實時的天氣預報,其使用的模式充分利用四維同化資料,可提供全球在65 公里高度內60 層的40公里網格密度共兩千萬個點的風、氣溫、濕度預報。借此我們使用了2017-2019 年風場數據,數據間隔為6小時。使用第三代近岸波浪模型(SWAN)模擬了3 年中每小時波高,計算區域位于中國黃渤海,經度范圍117°E-123°E,緯度范圍35°N-41°N,地形水深數據來源于海圖的實測精確數據。計算網格為三角形網格,共計15369 個,最大精度為0.5km 考慮了包括白蓋、破波、底摩擦在內的波能耗散機制,波浪高度和波浪周期具有更高精確度。
為證明模擬結果的可信性,與國家海洋信息中心聯系,取得了成山頭測站(122.69°E,37.38°N)的2017 年2-4 月、2018 年2-4 月、2019 年2-4 月的實測波高數據,與模擬結果進行對比,除了實測數據有缺失的部分,模擬波高和實測數據擬合較好。為了量化模擬性能,結合了兩者的相關性分析,相關系數(R)為0.81,均方根誤差(RMSE)也較小,說明SWAN 模型能夠較準確地模擬本地區波高的時間變化。
2.2 Gumbel 波高極值分布
Gumbel 分布的基本方法為:對于一系列的k 個隨機變量(如波高值),其原始分布函數為G(x),如果在同一條件下(如黃渤海地區的氣象要素),作n 次取樣,能得到n 組隨機變量,每組變量的最大項便可以組成一個波高極值分布。最大項的極值分布函數F(x)和原始分布函數的關系為:
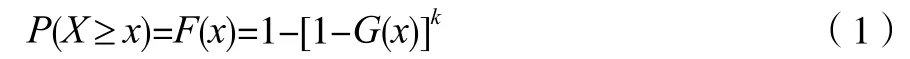
其中,原始分布G(x)為指數分布,近似寫作:

當變量數充分大,即k 趨近于∞時,式子(1)變為:
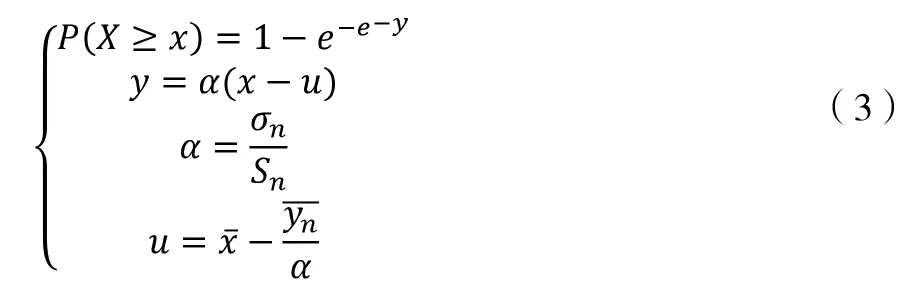
其中,Sn為樣本標準差,σn和yn與累積頻率P 有關,是項目n 的函數,所以當n 確定后,由P=m/(n+1)可以求得σn和yn的值,m 為k 個變量按照遞減次序排列的序號,最后可以求得對于一定重現期頻率的P,其對應的重現波高xp為:

根據上述Gumbel 分布的方法,對于波高模擬值結果,選擇了成山頭測站位置點處連續31 天的數據進行極值分析,得到的波高極值分布如圖1 所示,黑色點表示的是波高模擬結果,藍色曲線表示了根據Gumbel分布函數得到的預測曲線,兩條線的擬合程度的相關系數(R)為0.79,均方根誤差(RMSE)為0.21,表明Gumbel 分布對于本地波高極大值的擬合程度較好,可以作為預測預報的參考。需要注意的是,圖中表示的是某一預測時間段內的波高預測值得最大值,例如:x 軸上預測天數為100 天表示的是未來100 天內出現的最大波高值約為1.59m,是一個統計概念,而并非指未來第100 天的波高值為1.59m。[2]
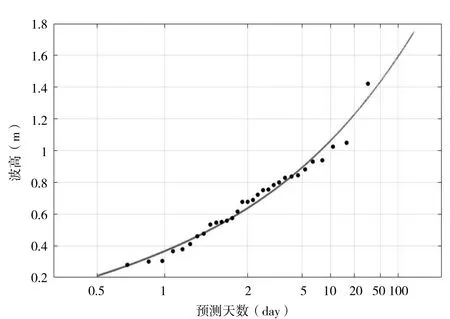
圖1 模擬波高與Gumbel 分布擬合結果
2.3 Person Ⅲ型波高極值分布
Person Ⅲ型分布最初由英國K·Person 在生物學統計分析中提出,他發現概率密度曲線的圖形是單峰式的,即只有一個眾值,在峰頂兩旁的出現概率密度逐漸減小,且曲線的兩端或者一端與橫軸漸近相切,基于此,他建立了概率密度曲線的微分方程式:

如果將坐標原點移動至波高序列變量的實際零點,則可以得到Person Ⅲ型曲線的常見形式:
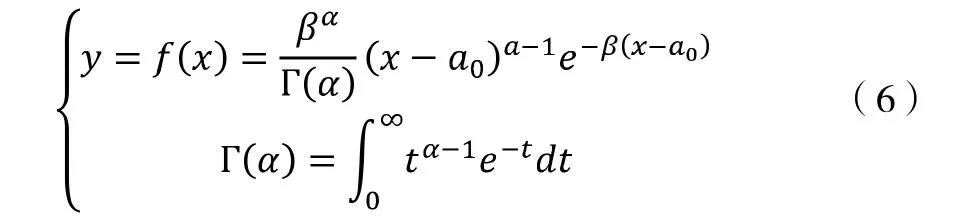
式中α、β、a0為待定參數,他們與統計分析量均
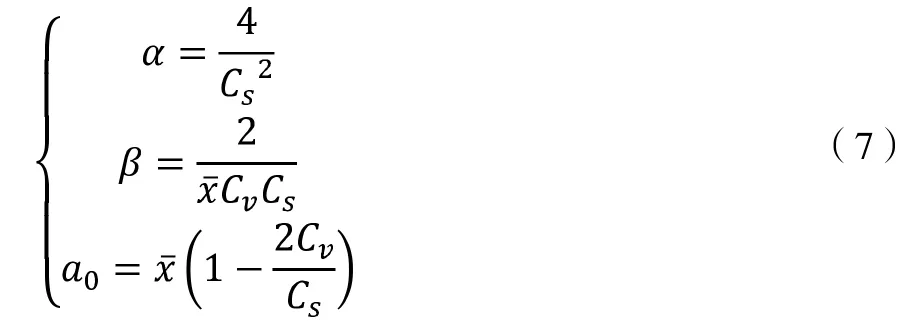

根據上述Person Ⅲ型分布的方法,對于波高模擬值結果,使用與上述Gumbel 分布擬合所用相同的數據,得到的擬合結果如圖2 所示。圖中黑色點表示的是波高模擬結果,紅色曲線表示根據Gumbel 分布函數得到的預測曲線,兩條線的擬合程度的相關系數(R)為0.83,均方根誤差(RMSE)為0.20,表明Person Ⅲ型分布對于本地波高極大值的擬合程度較好,同樣可以作為預測預報的參考。其橫縱坐標的含義同圖2 的Gumbel 分布是一致的。
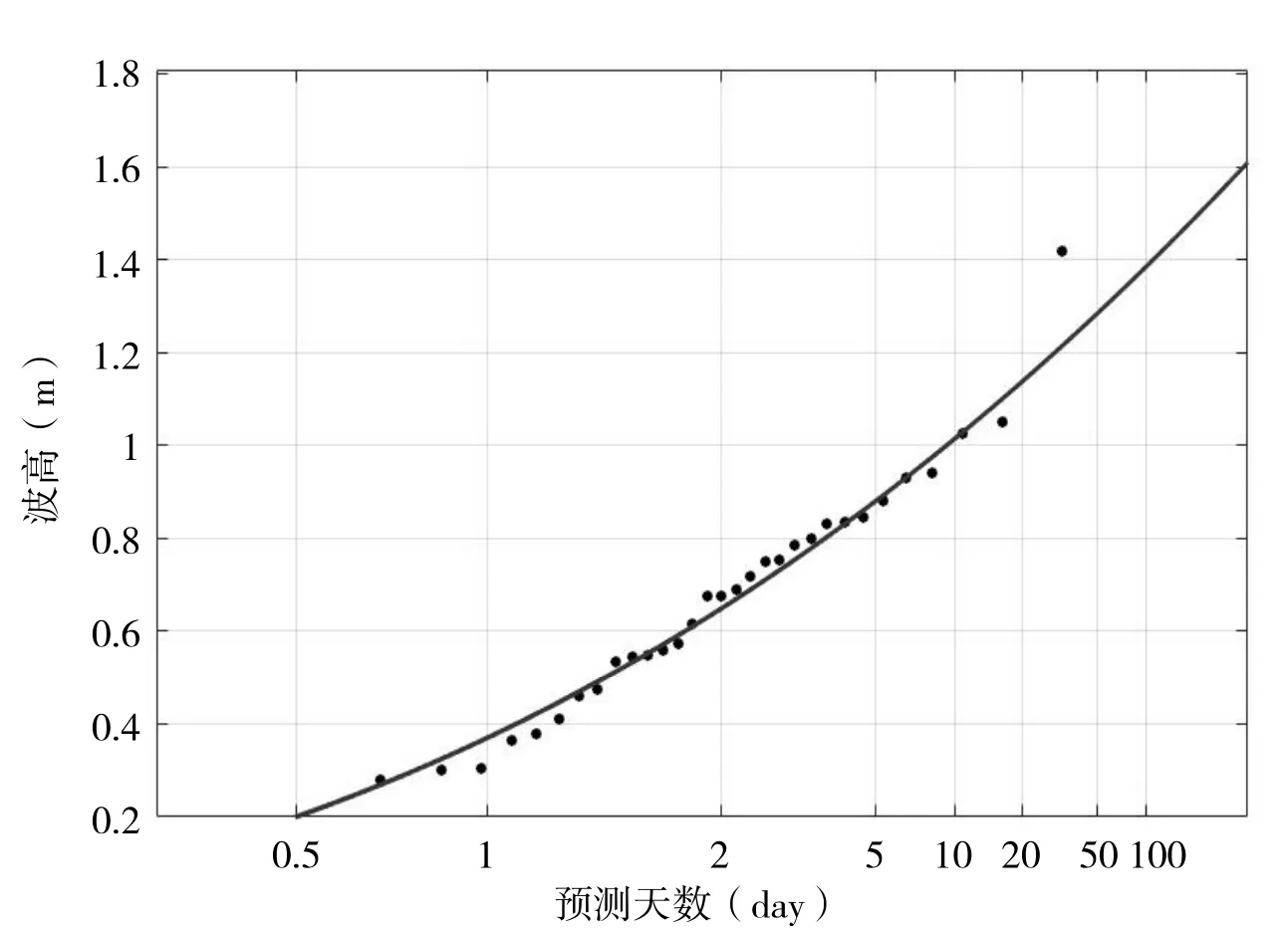
圖2 模擬波高與Person Ⅲ型分布擬合結果
綜合Gumbel 和Person Ⅲ型兩種分布來看,兩種方法均能較好地擬合波高的模擬值情況,但是有所區別:對于預測時間較長的情況下(如30 天以上),Gumbel方法預測的極端大值更貼合于實際的模擬結果,曲線形狀更為上揚,這也決定了其對于較短預測天數情況下(如30 天以下)的波高極端值會偏大。而Person Ⅲ型分布方法恰好相反,其曲線特征腹部與實際模擬結果更為貼合,對于短預測天數情況下(如30 天以下)的波高極端值擬合更好,對于長期(如30 天以上)的預測結果會偏小一些。
3 結論及應用
本文首先使用歐洲天氣預報中心(ECMWF)風場,利用SWAN 數值模型再現了黃渤海海域的波高分布情況,然后與成山頭測站的實測波浪值進行對比,相關性表明模擬的結果較好,肯定了在黃渤海海域根據實時風場或者預報風場進行波高預測的可行性。
由于氣象風場預測的時長有限性,結合測站測點覆蓋的局部性,因此使用統計學的方法,對于黃渤海海域全局模擬的波高進行統計學分析,利用Gumbel 型分布函數Person Ⅲ型分布函數來進行極端波高的預測預報,并根據擬合的結果,判定當需要預測的波高天數大于30 天時,推薦使用Gumbel 分布,當需要預測的波高天數小于30 天時,推薦使用Person Ⅲ型分布。這種綜合判斷分析預報的方法,可以更好地為后續與波高有關的工程建設、民商互動和船舶作業提供參考決策。

