貨車(chē)轉(zhuǎn)向架相對(duì)摩擦因數(shù)設(shè)計(jì)值和試驗(yàn)結(jié)果差異分析
劉振明
(中車(chē)齊齊哈爾車(chē)輛有限公司 大連研發(fā)中心,遼寧 大連 116052)
彈簧減振裝置是鐵路貨車(chē)轉(zhuǎn)向架的重要部件,相對(duì)摩擦因數(shù)是其關(guān)鍵參數(shù),直接影響車(chē)輛動(dòng)力學(xué)性能[1-2]。多年實(shí)踐表明,實(shí)測(cè)相對(duì)摩擦因數(shù)往往和設(shè)計(jì)值存在一定差異。本文將對(duì)兩者之間的差異原因進(jìn)行分析,定量地給出差異程度,并給出協(xié)調(diào)兩者的具體建議。
1 摩擦楔塊式減振器結(jié)構(gòu)和作用原理
鐵路貨車(chē)鑄鋼三大件式轉(zhuǎn)向架一般采用摩擦楔塊式減振器,可分為變摩擦和常摩擦2種結(jié)構(gòu)(圖1),2種減振器的楔塊受力分析如圖2、圖3所示。
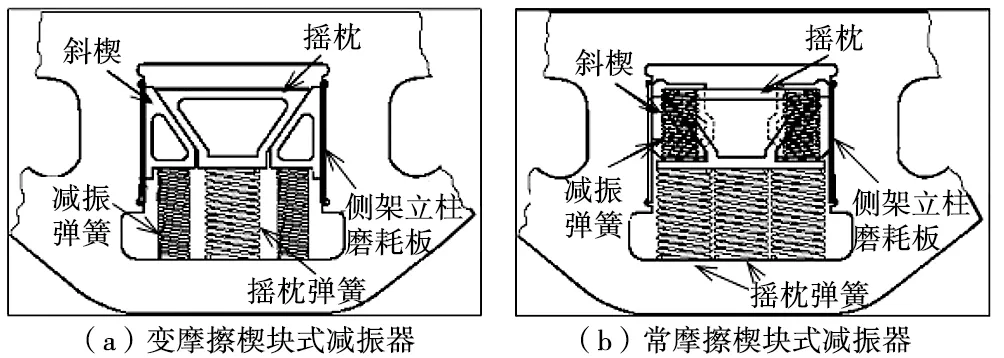
圖1 摩擦楔塊式減振器結(jié)構(gòu)
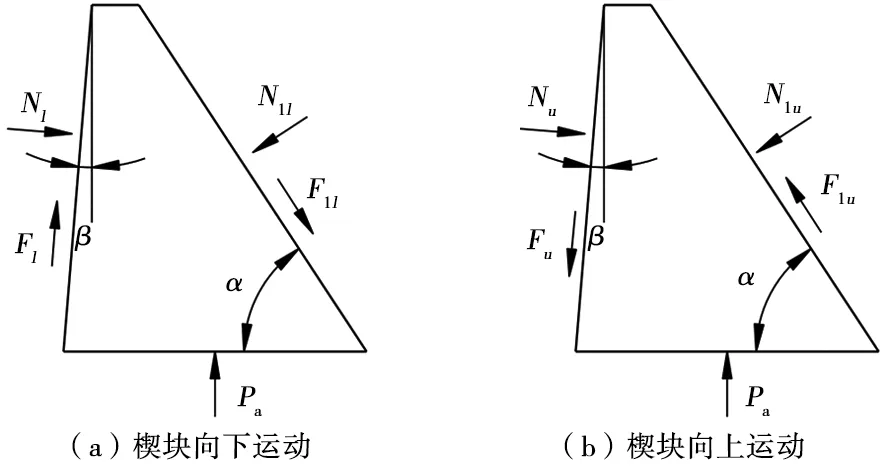
圖2 變摩擦減振器楔塊受力分析
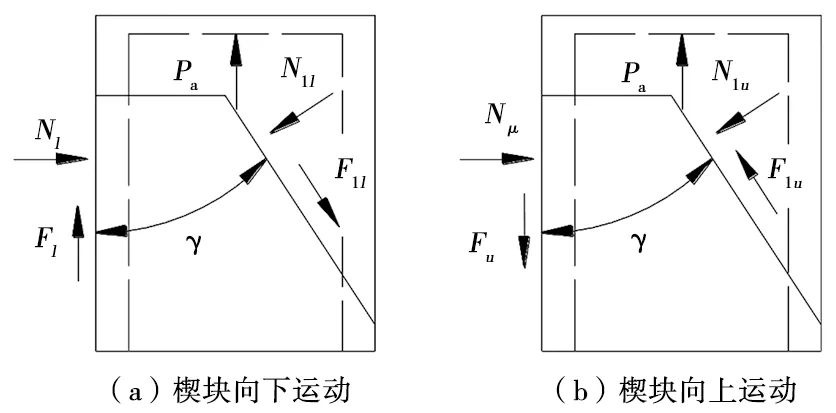
圖3 常摩擦減振器楔塊受力分析
2 相對(duì)摩擦因數(shù)定義計(jì)算方法及特性
2.1 相對(duì)摩擦因數(shù)定義[3-4]
楔塊式減振器阻尼的大小通常用相對(duì)摩擦因數(shù)φ來(lái)表示,它是摩擦力與垂向力的比值(以下簡(jiǎn)稱(chēng)“定義力比法”),一般只用主摩擦面上的摩擦力來(lái)計(jì)算(副摩擦面的摩擦功占比很小,略去不計(jì)),即:
(1)
式中:Fu——楔塊向上運(yùn)動(dòng)時(shí),一個(gè)楔塊主摩擦面的摩擦力;
Fl——楔塊向下運(yùn)動(dòng)時(shí),一個(gè)楔塊主摩擦面的摩擦力;
P——搖枕每端彈簧垂向反力總和。
2.2 定義力比法計(jì)算相對(duì)摩擦因數(shù)
2.2.1 變摩擦減振器(減振簧與枕簧等高)
對(duì)于變摩擦減振器(圖2),式(1)中的P為:
P=nKz+2Pa
(2)
式中:n——搖枕每端枕簧組數(shù);
K——每組枕簧的垂向剛度;
z——搖枕垂向位移,即枕簧撓度;
Pa——一個(gè)楔塊上的彈簧垂向反力。
Fu、Fl可用以下公式表示:
(3)
(4)
其中:
Δu=(1+μμ1)cos(α-β)-(μ1-μ)sin(α-β)
(5)
Δl=(1+μμ1)cos(α-β)+(μ1-μ)sin(α-β)
(6)
式中:μ——主摩擦面摩擦因數(shù);
μ1——副摩擦面摩擦因數(shù);
α——楔塊副摩擦面與水平面夾角;
β——楔塊主摩擦面與垂直面夾角;
K1——減振簧垂向剛度;
z1——楔塊垂向位移。
由式(1)可知,按定義力比法得出的φ是根據(jù)某一給定彈簧撓度下各力計(jì)算得出的數(shù)值,當(dāng)減振簧與枕簧等高時(shí),楔塊下移量就是減振簧壓縮量,可得:
(7)
(8)
可見(jiàn),φ僅與K、K1、α、β、μ、μ1有關(guān)。如果此時(shí)K=K1,則式(7)可簡(jiǎn)化為:
(9)
此時(shí)φ為定值,無(wú)論枕簧撓度多大,φ都相同。
以轉(zhuǎn)8A型轉(zhuǎn)向架為例,代入各參數(shù)后求得其P、Fu、Fl、φ與枕簧撓度的關(guān)系如圖4、圖5所示。
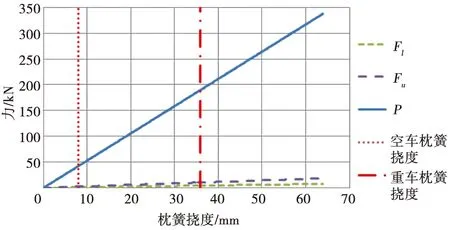
圖4 P、Fu、Fl與枕簧撓度的關(guān)系

圖5 φ與枕簧撓度的關(guān)系
2.2.2 變摩擦減振器(減振簧加高)
為了緩解楔塊磨耗后上升、減振簧壓縮量變小導(dǎo)致的減振力不足,設(shè)計(jì)時(shí)一般使減振簧高度大于枕簧高度[5-6]。當(dāng)減振簧加高時(shí),得到:
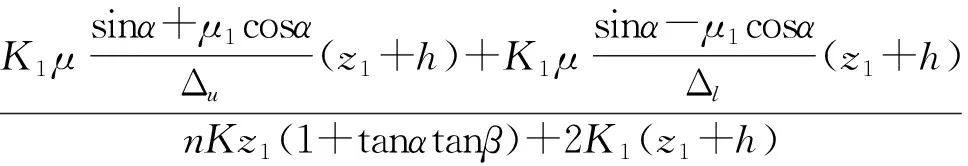
(10)
式中:h——減振簧比枕簧高出值。
可見(jiàn),φ不僅與K、K1、α、β、μ、μ1有關(guān),還與h、z1有關(guān),h為常數(shù),z1可用z的函數(shù)表達(dá),而z是變量,因此φ是一個(gè)隨z變化的值,即相對(duì)摩擦因數(shù)與彈簧撓度有關(guān)。
以轉(zhuǎn)K2型轉(zhuǎn)向架為例,代入各參數(shù)后求得其P、Fu、Fl、φ與減振簧撓度的關(guān)系如圖6、圖7所示。
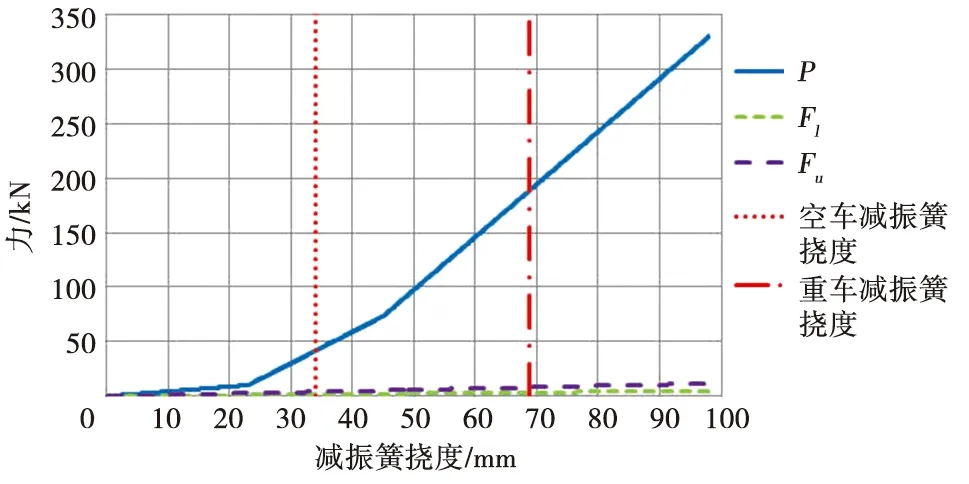
圖6 P、Fu、Fl與減振簧撓度的關(guān)系
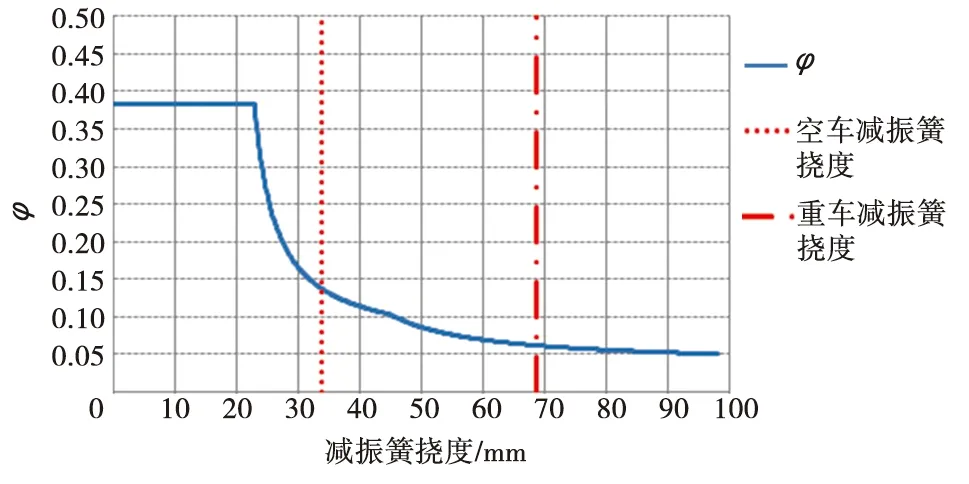
圖7 φ與減振簧撓度的關(guān)系
2.2.3 常摩擦減振器
常摩擦減振器的楔塊受力中,主摩擦面為垂直面(圖3)。因結(jié)構(gòu)不同,計(jì)算其相對(duì)摩擦因數(shù)時(shí),搖枕每端彈簧垂向反力總和不再含有楔塊上的減振簧反力[7-8]。通過(guò)受力分析(因主摩擦面為垂直面,因此假設(shè)斜楔斜面與搖枕斜楔槽斜面間無(wú)相對(duì)運(yùn)動(dòng)趨勢(shì),即圖3中斜面上的F1u=0、F1l=0),求得Fu、Fl可用以下公式表示:
(11)
(12)
式中:f——減振簧垂向壓縮量,常數(shù);
γ——楔塊副摩擦面與主摩擦面夾角。
將P、Fu、Fl代入式(1),得:
(13)
由式(1)及式(13)可知,常摩擦減振器的φ與K、K1、γ、μ、μ1、n、f、z有關(guān),因?yàn)閦是變量,其余為常數(shù),因而隨著枕簧撓度的不同,φ也隨之變化;z變大時(shí),φ變小。
以轉(zhuǎn)D21型轉(zhuǎn)向架為例,代入各參數(shù)后求得其P、Fu、Fl、φ與枕內(nèi)簧撓度(內(nèi)簧高于外簧)的關(guān)系如圖8、圖9所示。
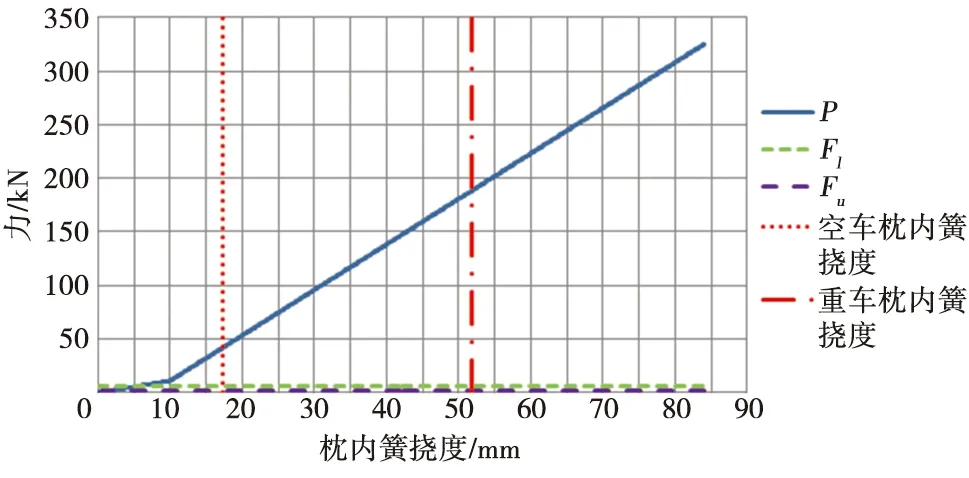
圖8 P、Fu、Fl與枕內(nèi)簧撓度的關(guān)系
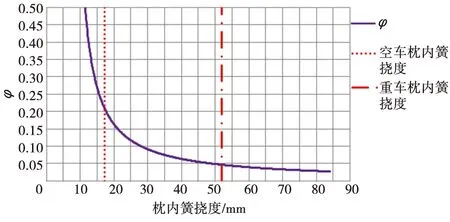
圖9 φ與枕內(nèi)簧撓度的關(guān)系
3 標(biāo)準(zhǔn)測(cè)定方法與定義力比法的差異
3.1 標(biāo)準(zhǔn)測(cè)定方法
GB/T 5599—2019《機(jī)車(chē)車(chē)輛動(dòng)力學(xué)性能評(píng)定及試驗(yàn)鑒定規(guī)范》附錄A規(guī)定,相對(duì)摩擦因數(shù)測(cè)定方法是:“試驗(yàn)時(shí)對(duì)轉(zhuǎn)向架心盤(pán)平穩(wěn)地逐級(jí)施加垂向載荷,加至最大試驗(yàn)載荷后,再平穩(wěn)地逐級(jí)減載至零位。最大試驗(yàn)載荷不應(yīng)小于轉(zhuǎn)向架簧上靜載荷”,加載曲線如圖10所示。
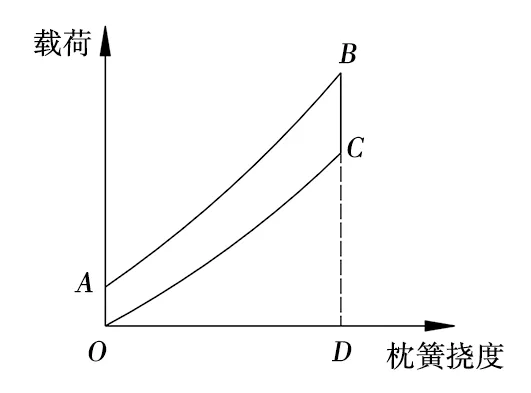
圖10 加載曲線
相應(yīng)的相對(duì)摩擦因數(shù)φ1計(jì)算方法為[9]:
(14)
對(duì)比式(14)與式(1)可知,式(1)采用某一給定彈簧撓度時(shí)瞬時(shí)力比值計(jì)算理論相對(duì)摩擦因數(shù),而圖10和式(14)采用載荷從零到某一給定心盤(pán)載荷時(shí)加減載曲線所圍成的各面積比值計(jì)算(以下簡(jiǎn)稱(chēng)“試驗(yàn)面積比法”)。由于方法不同,兩者將在理論上產(chǎn)生計(jì)算結(jié)果差異。
3.2 試驗(yàn)面積比法計(jì)算相對(duì)摩擦因數(shù)
3.2.1 變摩擦減振器(減振簧與枕簧等高)
對(duì)于變摩擦減振器,當(dāng)減振簧與枕簧等高時(shí),理想加載曲線如圖11所示,即A點(diǎn)與O點(diǎn)重合,各面積均為三角形[10],將三角形面積計(jì)算公式代入式(14),得:
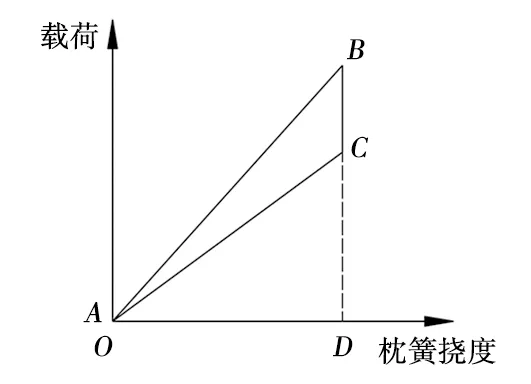
圖11 理想加載曲線
(15)
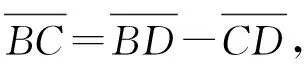
(16)
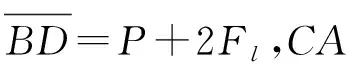
(17)
對(duì)比式(17)與式(1)可知,按定義力比法計(jì)算φ值時(shí)分母為彈簧垂向反力P,不包含摩擦力Fu、Fl,而按試驗(yàn)面積比法計(jì)算φ1值時(shí),分母包含了摩擦力Fu、Fl。根據(jù)式(3)、式(4)可知,F(xiàn)l
以轉(zhuǎn)8A型轉(zhuǎn)向架為例,φ1是φ的1.033倍,如圖12所示。
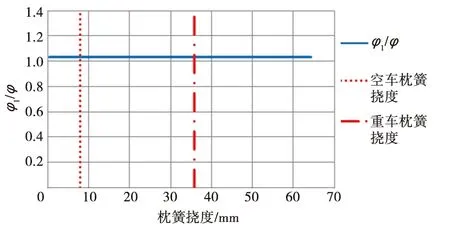
圖12 φ1/φ與枕簧撓度的關(guān)系
3.2.2 變摩擦減振器(減振簧加高)
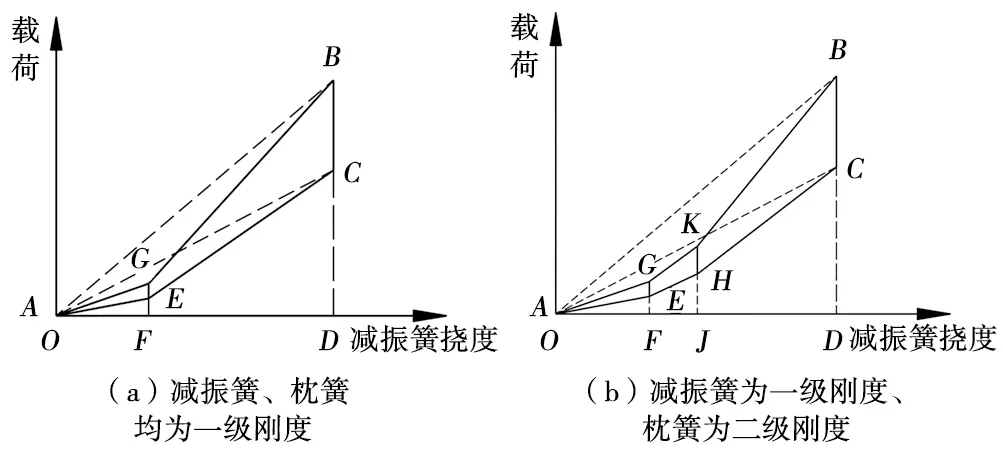
圖13 減振簧加高時(shí)的加載曲線
按試驗(yàn)面積比法進(jìn)行計(jì)算,可得:

(18)
將三角形、梯形面積計(jì)算公式代入,得:
(19)
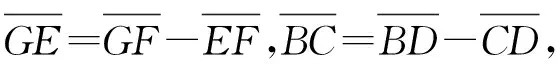
(20)
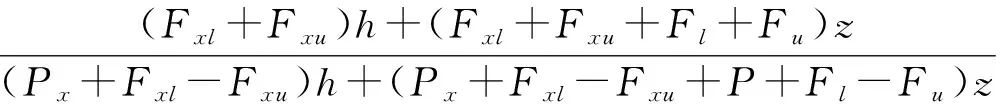
(21)
可見(jiàn),式(21)與式(17)很相似,但增加了減振器結(jié)構(gòu)參數(shù)h和搖枕位移z,根據(jù)上述分析,此時(shí)如果還按式(17)計(jì)算,則計(jì)算出的φ1其實(shí)是圖13(a)中加載曲線為AB、AC時(shí)的值,反映不出G、E點(diǎn)對(duì)面積比的影響,所以會(huì)產(chǎn)生誤差。
與3.2.1同理,式(21)與式(1)的分子分母均不同,由于較復(fù)雜,不能直接判斷出φ1與φ的大小,必須按實(shí)際參數(shù)計(jì)算。
如果減振簧為一級(jí)剛度、枕簧為二級(jí)剛度,則試驗(yàn)加載曲線如圖13(b)所示的實(shí)線圖形,即AGKBCHE,這時(shí)如果加載枕簧撓度位于FJ間,則φ1的求解公式類(lèi)似式(21)。如果位于JD間,則可用試驗(yàn)面積比法按同樣的過(guò)程推導(dǎo)出φ1的求解公式如下:
(22)
式中:Px——減振簧壓縮h時(shí)搖枕一端的彈簧垂向反力;
Fyu——第1級(jí)枕簧(高枕簧)壓縮h1、楔塊向上運(yùn)動(dòng)時(shí)一個(gè)楔塊主摩擦面的摩擦力;
Fyl——第1級(jí)枕簧壓縮h1、楔塊向下運(yùn)動(dòng)時(shí)一個(gè)楔塊主摩擦面的摩擦力;
Py——第1級(jí)枕簧壓縮h1時(shí)搖枕一端的彈簧垂向反力;
z2——以第2級(jí)枕簧(矮枕簧)計(jì)算的壓縮量;
h1——兩級(jí)枕簧高度差。
以符合上述情況的轉(zhuǎn)K2型轉(zhuǎn)向架為例,φ1是φ的1.75倍(空車(chē))和1.44倍(重車(chē)),其隨減振簧撓度的變化趨勢(shì)如圖14所示。
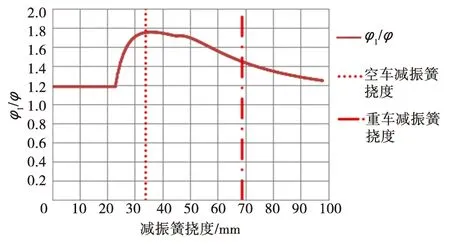
圖14 φ1/φ與減振簧撓度的關(guān)系
轉(zhuǎn)K2型轉(zhuǎn)向架按試驗(yàn)力比法公式(17)求得的φ2是φ的1.059倍(空車(chē))和1.025倍(重車(chē)),其隨減振簧撓度的變化趨勢(shì)如圖15所示。

圖15 φ2/φ與減振簧撓度的關(guān)系
3.2.3 常摩擦減振器
對(duì)于常摩擦減振器,如圖16(a)所示,最初從平衡位置O點(diǎn)加載,由于存在一個(gè)常摩擦力,因此先到A點(diǎn),期間枕簧撓度不變,然后至B點(diǎn),減載時(shí)沿BCF至載荷為0的F點(diǎn)。由于常摩擦力的存在,枕簧撓度不能回到平衡位置O點(diǎn),而是止于F點(diǎn),再次加載、減載則沿FEBC循環(huán)進(jìn)行,AE段僅第1次加載時(shí)經(jīng)過(guò),因Fu、Fl為常數(shù),故FEBC為平行四邊形。
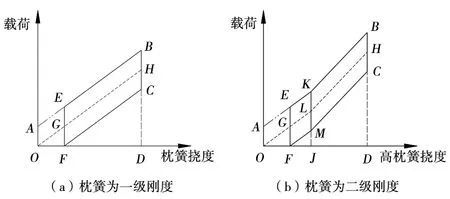
圖16 常摩擦減振器加載曲線
考慮到一般測(cè)試要循環(huán)幾次,所以應(yīng)忽略第1次加載的AE段,此時(shí)按試驗(yàn)面積比法計(jì)算,可得:
(23)
按圖16(a),將三角形、梯形、平行四邊形面積計(jì)算公式代入,得:
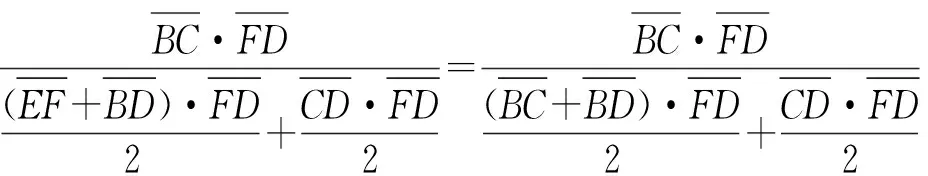
(24)
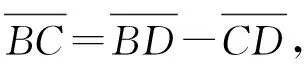
(25)
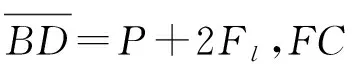
(26)
化簡(jiǎn)得:
(27)
對(duì)比式(27)與式(1)可知,當(dāng)Fl=P/2時(shí),式(27)可化簡(jiǎn)為式(1),兩者等效;當(dāng)Fl
如果枕簧為二級(jí)剛度,則試驗(yàn)加載曲線為圖16(b)所示的實(shí)線圖形,即FEKBCM,這時(shí)如果加載枕簧撓度位于FJ間,則φ1的求解公式類(lèi)似式(27)。如果位于JD間,則可用試驗(yàn)面積比法按同樣的過(guò)程推導(dǎo)出φ1的求解公式如下:
(28)
以符合上述情況的轉(zhuǎn)D21型轉(zhuǎn)向架為例,φ1是φ的2.11倍(空車(chē))和2.19倍(重車(chē)),其隨枕內(nèi)簧撓度的變化趨勢(shì)如圖17所示。
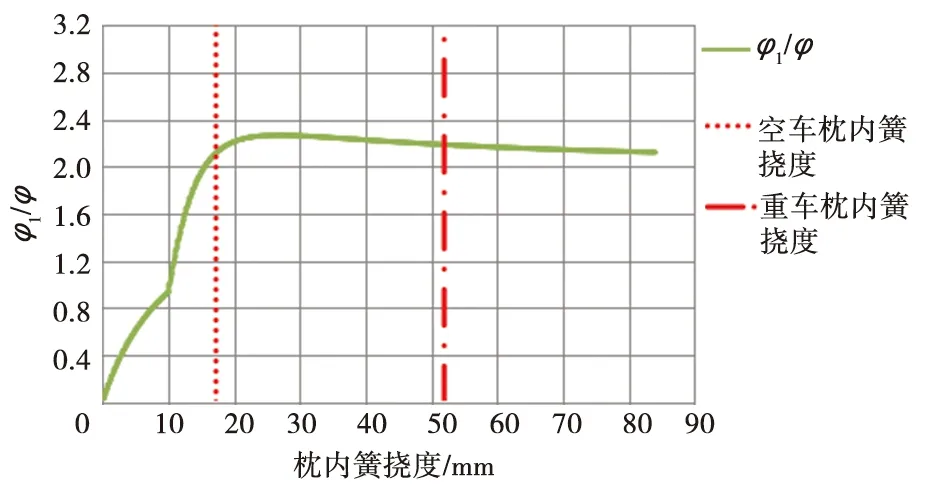
圖17 φ1/φ與枕內(nèi)簧撓度的關(guān)系
轉(zhuǎn)D21型轉(zhuǎn)向架按試驗(yàn)力比法公式(17)求得的φ2是φ的0.912倍(空車(chē))和0.979倍(重車(chē)),其隨減振簧撓度的變化趨勢(shì)如圖18所示。
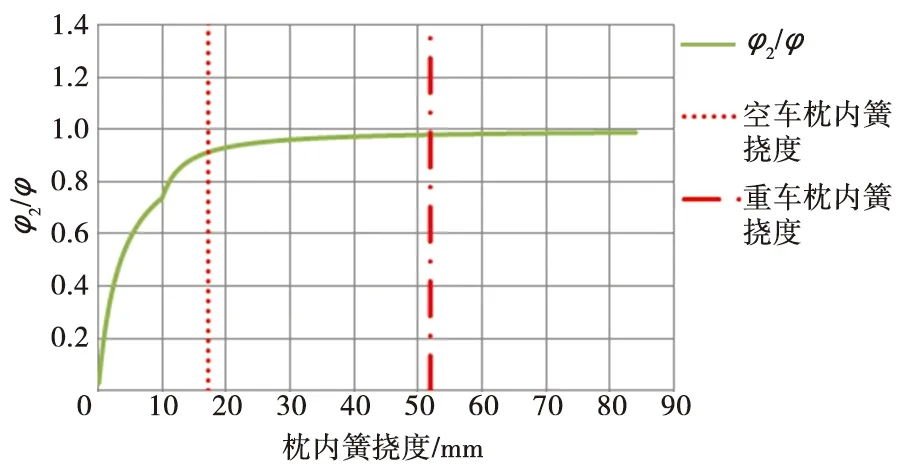
圖18 φ2/φ與枕內(nèi)簧撓度的關(guān)系
4 建議
為了使測(cè)試結(jié)果可用,避免試驗(yàn)和設(shè)計(jì)之間由于方法不同導(dǎo)致差異,建議采用如下2種方式進(jìn)行相對(duì)摩擦因數(shù)的測(cè)試和計(jì)算:
(1) 按試驗(yàn)面積比法測(cè)試并計(jì)算出相對(duì)摩擦因數(shù)后,利用本文所給出的公式,求出試驗(yàn)面積比法與定義力比法之間的關(guān)系,反算出按定義力比法的數(shù)值并與設(shè)計(jì)值對(duì)比;
(2) 按試驗(yàn)力比法計(jì)算相對(duì)摩擦因數(shù),利用本文所給出的公式,求出試驗(yàn)力比法與定義力比法之間的關(guān)系,反算出按定義力比法的數(shù)值并與設(shè)計(jì)值對(duì)比。

