基于永磁直驅城軌車輛的空氣彈簧設計
梁小強,胡定祥,楊澤迎,張 麗,何斌斌,于 磊
(1.中唐空鐵科技有限公司,四川 成都 610041;2.中車南京浦鎮車輛有限公司,江蘇 南京 210031; 3.江蘇中車數字科技有限公司,江蘇 南京 210031;4.中車青島四方車輛研究所有限公司,山東 青島 266031)
永磁直驅城軌車輛為最高運營速度80 km/h、軸重14 t的B型車城軌車輛[1]。為滿足車輛使用性能技術要求[2],其轉向架采用無搖枕結構形式以適應小曲線的通過,故轉向架二系懸掛系統采用大曲囊形式的空氣彈簧,以滿足車輛的運動穩定性、曲線通過安全性和運行平穩性。
1 空氣彈簧結構
空氣彈簧是轉向架二系懸掛系統中最重要的一個部件,安裝在車體和構架之間,傳遞著垂向力和橫向力,平衡轉向架和車體之間產生的相對運動。具有小橫向剛度、大徑向位移的空氣彈簧能夠代替傳統客車轉向架的搖動臺和搖枕,有效簡化二系懸掛系統的結構,實現轉向架無搖動臺和無搖枕結構設計,同時避免中央懸掛裝置的磨耗[3]。
空氣彈簧結構如圖1所示,主要由上蓋組成、扣環、膠囊、支撐座、摩擦塊、橡膠堆等組成。
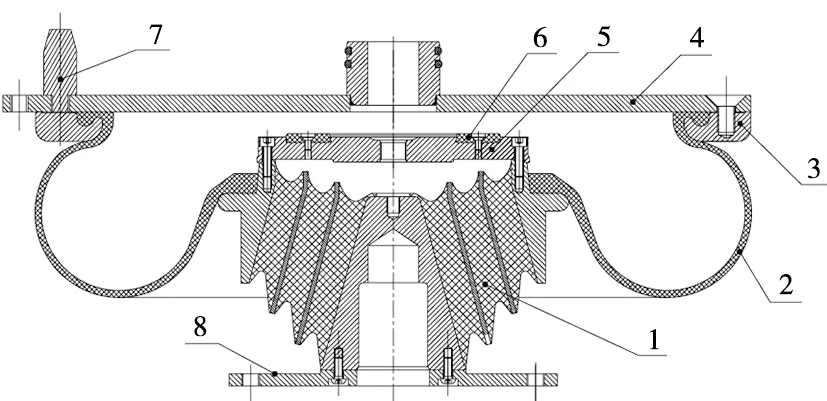
1.橡膠堆;2.膠囊;3.扣環;4.上蓋組成;5.支撐座;6.摩擦塊;7.定位銷;8.安裝座。圖1 空氣彈簧結構圖
2 空氣彈簧組成特點
空氣彈簧組成特點[4]如下:
(1) 剛度小,當量撓度大。空氣彈簧能大幅度地增加當量撓度,使彈簧懸掛裝置設計得很柔軟,如此可降低車輛的自振頻率。
(2) 具有非線性特性。空氣彈簧具有非線性特性,根據車輛振動性能的需要設計成具有比較理想的彈性特性曲線。在平衡位置低頻振動幅度較小時,即正常運行時的振動剛度較低;若位移過大,壓縮空氣或充氣使剛度顯著增加,可限制車體的振幅。
(3) 剛度隨載荷變化。空氣彈簧剛度隨載荷內壓變化而變化,從而可保持空重車狀態下車體自振頻率幾乎相等,使空重車不同狀態的運行平穩性基本相同。
(4) 高度可調節。空氣彈簧和高度閥裝置并用,可使車體在不同靜載荷下保持地板面距軌面的高度基本不變。
(5) 可充分利用其徑向彈性。空氣彈簧可同時承受三向載荷,具有較大的水平變位能力;利用空氣彈簧的橫向彈性特性,可以代替傳統轉向架的搖動臺裝置,從而簡化結構,減輕自重。
(6) 能產生阻尼作用。若在空氣彈簧本體和附加空氣室之間設有適宜的節流孔,可以產生適宜的阻尼,以代替垂向液壓減振器。
(7) 具有吸振和隔聲功能。空氣彈簧具有良好的吸收高頻振動和隔聲功能。
3 空氣彈簧參數設計
空氣彈簧主要技術參數有空氣彈簧水平變形能力(扭轉角度和最大水平位移)、載荷內壓、剛度(橫向剛度和垂向剛度)。
3.1 空氣彈簧水平變形能力
3.1.1 扭轉角度
車輛通過小曲線時,轉向架會相對車體旋轉和橫移,車體與轉向架的相對扭轉角即為空氣彈簧應能適應的扭轉角度。空氣彈簧扭轉角度計算時主要考慮2種情況:其一為轉向架在最小曲線半徑上的徑向位置并處于軌道中心線上,其二為前轉向架或后轉向架繞著角度增大方向發生前后輪對輪緣異向貼靠鋼軌位置[5]。
3.1.1.1轉向架處于軌道曲線徑向位置的扭轉角計算
假設前后轉向架均處于軌道曲線的徑向位置,并處于軌道中心線上,如圖2所示,此時轉向架相對車體的扭轉角為α。則扭轉角α為:
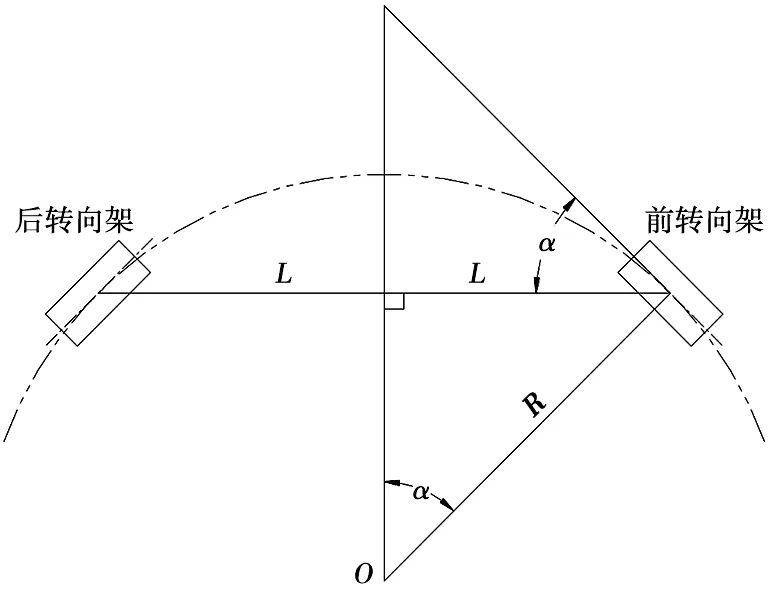
圖2 轉向架處于軌道曲線徑向位置的扭轉角
α=arcsin(L/R)
(1)
式中:L——車輛定距;
R——線路半徑。
3.1.1.2輪軌間隙引起的扭轉角計算
假設轉向架處于前后輪對輪緣異向貼靠鋼軌位置,如圖3所示,此時轉向架相對車體的扭轉角為β。
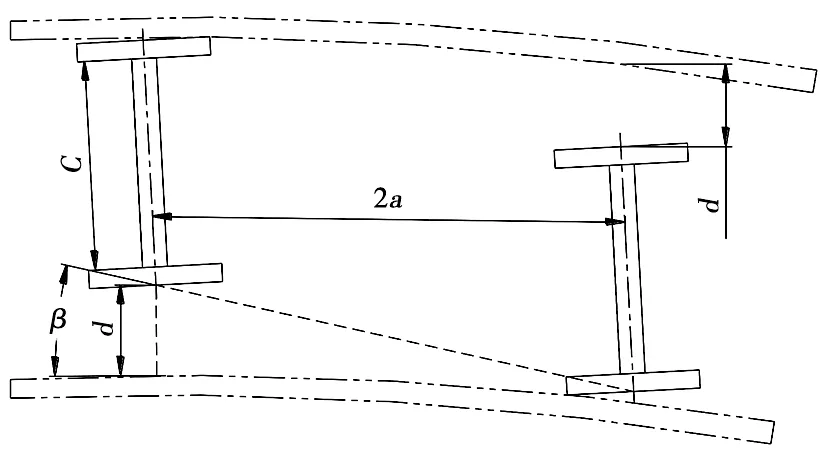
圖3 輪軌間隙引起的扭轉角
此時,扭轉角β為:
β=arcsin(d/2a)
(2)
輪軌間隙d為:
d=G+g+Ω1+Ω2+2ω-C-2τ
(3)
式中:2a——軸距;
G——名義軌距;
g——曲線軌距加寬;
Ω1——軌距公差的正值,不含軌距加寬;
Ω2——輪對內側距公差負值的絕對值;
ω——輪緣最大磨耗量;
C——名義輪對內側距;
τ——輪緣厚度。
3.1.1.3空氣彈簧扭轉角計算
由前文可得,空氣彈簧扭轉角φ為:
φ=α+β
(4)
永磁直驅轉向架相對車體的扭轉角計算參數如表1所示。

表1 永磁直驅轉向架相對車體的扭轉角計算參數
(1) 段內扭轉角φ1計算如下:
d=G+g+Ω1+Ω2+2ω-C-2τ=64 (mm)
φ1=α+β=0.091 rad≈5.21°
(2) 正線扭轉角φ2計算如下:
d=G+g+Ω1+Ω2+2ω-C-2τ=59 (mm)
φ2=α+β=0.056 3 rad≈3.23°
因此,空氣彈簧扭轉角φ在惡劣工況下約為5.21°。
3.1.2 空氣彈簧水平位移
空氣彈簧在極端工況(段內小曲線運行)下除需適應扭轉角外,還應當具有一定的橫向水平變形能力。空氣彈簧水平位移產生條件主要有轉向架相對車體扭轉角φ、橫向擋壓并、車體相對轉向架最大縱向位移,如圖4所示。
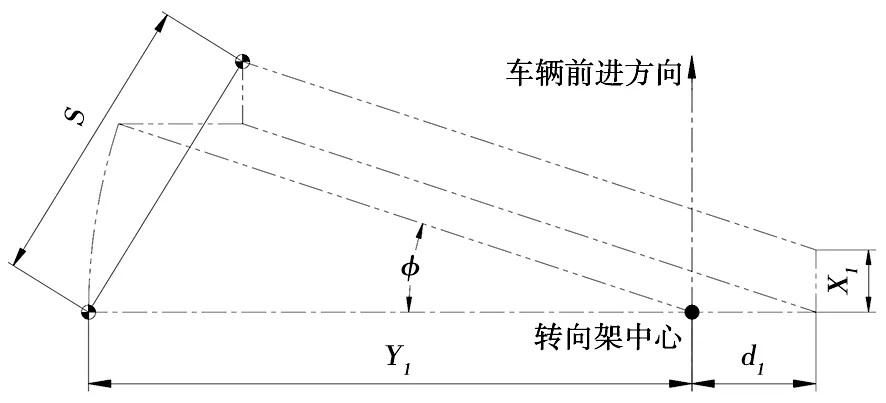
S.空氣彈簧水平位移;Y1.空氣彈簧橫向跨距之半;X1.相對轉向架車體最大縱向位移(一般取縱向擋間隙);d1.橫向檔間隙和壓縮量。圖4 空氣彈簧水平位移與扭轉角、橫向位移、縱向位移的關系
永磁直驅轉向架空氣彈簧水平位移計算參數如表2所示。

表2 永磁直驅轉向架空氣彈簧水平位移計算參數(極限位置)
空氣彈簧水平位移S計算如下:
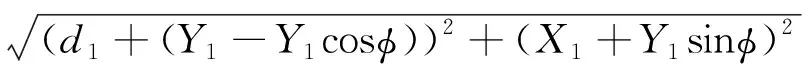
≈104.6 mm
因此,空氣彈簧在極端工況下的最大水平位移為104.6 mm。
3.2 空氣彈簧載荷內壓
為滿足車輛的最大承載及設計冗余,永磁直驅轉向架用空氣彈簧最大承載載荷為120 kN。空氣彈簧內壓需求應與車輛總體技術條件相匹配,車輛制動系統列車總風管供風壓力一般為750~900 kPa,結合空氣彈簧廠商確定滿足車輛需求的載荷內壓,以及TB/T 2841—2010《鐵道車輛空氣彈簧》的壓力載荷特性取值要求和最大水平位移下的壓力需求,永磁直驅用空氣彈簧最大載荷工況下的內壓需求不超過650 kPa(運用氣壓值),滿足車輛總體供風條件,壓力載荷特性見表3。

表3 壓力載荷特性
3.3 空氣彈簧剛度
通過對車輛系統進行蛇行運動穩定性、曲線通過性能和運行平穩性動力學計算分析,分別計算動拖車空載工況下空氣彈簧橫向剛度對平穩性的影響[6-8],結果如圖5、表4所示。
從圖5和表4可以看出,垂向剛度基本不變的情況下,橫向平穩性指標隨著橫向剛度的增加而增大,在0.2 MN/m范圍內均小于2.5。為保證車輛運行平穩性及設計冗余性,動拖車空氣彈簧空載工況(AW0)下橫向剛度選取0.16 MN/m較為適宜,可保證平穩性指標仍有約40%的冗余。

表4 空氣彈簧橫向剛度對平穩性的影響(80 km/h)
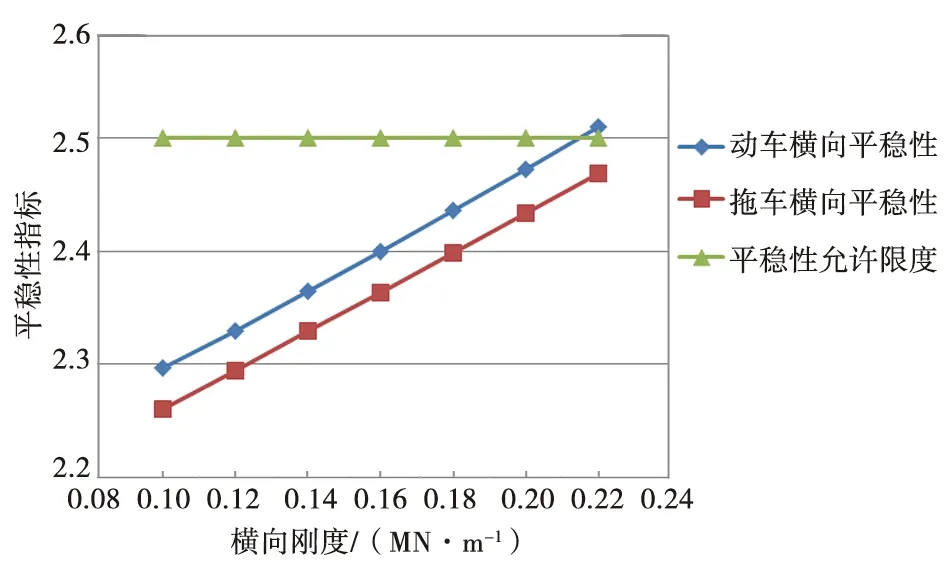
圖5 空氣彈簧橫向剛度對平穩性的影響(80 km/h)
空氣彈簧垂向剛度對平穩性的影響如圖6、表5所示。從圖6和表5可以看出,橫向剛度基本不變的情況下,垂向平穩性指標隨著垂向剛度的增加而增大,在0.6 MN/m范圍內均小于2.5。為保證車輛運行平穩性及設計冗余性,動拖車空氣彈簧空載工況(AW0)下垂向剛度選取0.6 MN/m較為適宜,可保證平穩性指標仍有約60%的冗余。

表5 空氣彈簧垂向剛度對平穩性的影響(80 km/h)
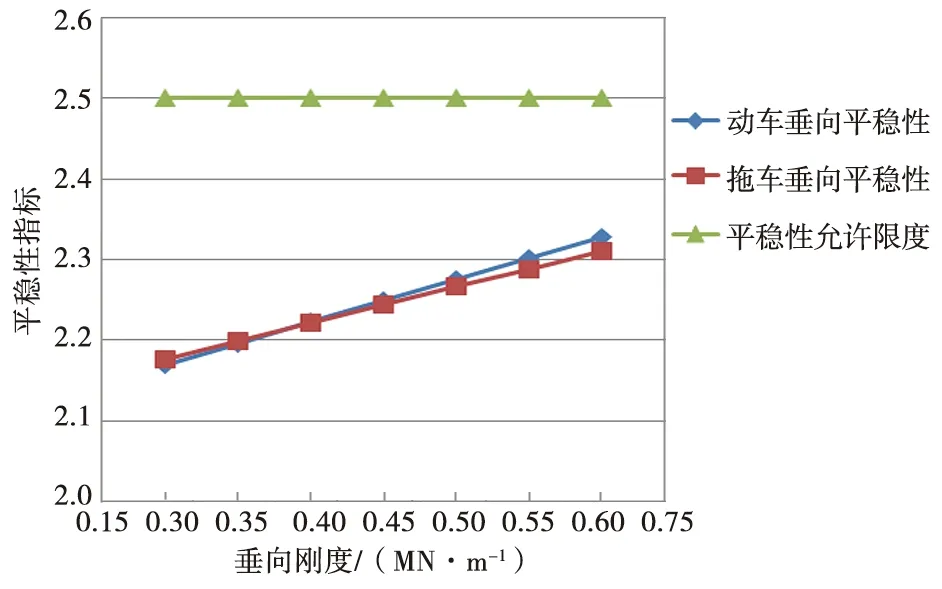
圖6 空氣彈簧垂向剛度對平穩性的影響(80 km/h)
由上述計算結果可以看出,平穩性指標滿足標準GB/T 5599—2019中1級“優”,由此表明,設計滿足車輛橫向和垂向運行平穩性指標。
4 試驗驗證
根據產品型式試驗報告及首件現場抽查審核鑒定,對空氣彈簧剛度(橫向剛度和垂向剛度)、最大水平位移下的外觀、載荷內壓等進行試驗驗證。
4.1 空氣彈簧剛度
4.1.1 垂向剛度
動拖車空載工況(AW0)下垂向剛度試驗相關數據見表6。由表6可知,在動拖車空載工況(AW0)下,空氣彈簧的垂向剛度實測值為478 N/mm,滿足設計要求。
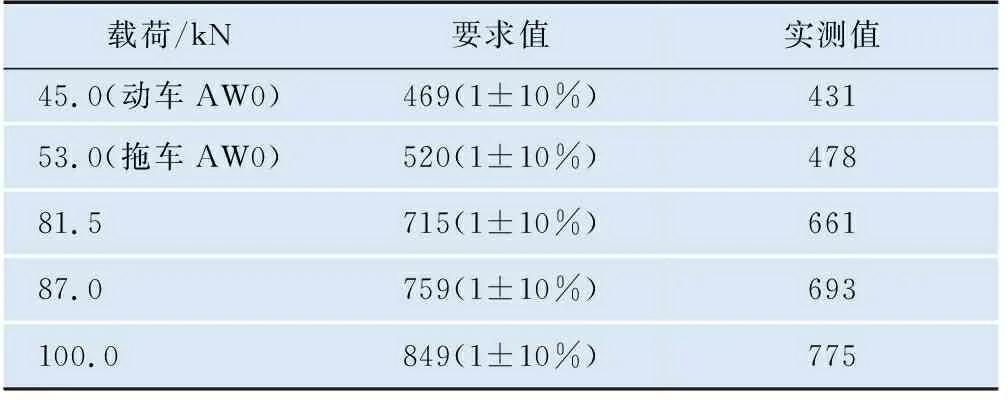
表6 空氣彈簧垂向剛度 N/mm
4.1.2 橫向剛度
動拖車空載工況(AW0)下橫向剛度試驗相關數據見表7。
由表7可以看出,在動拖車空載工況(AW0)下,空氣彈簧的橫向剛度實測值為150 N/mm,滿足設計要求。
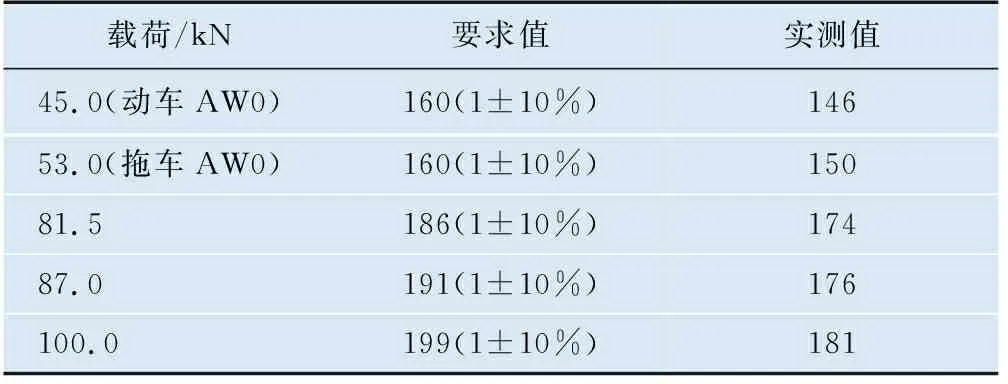
表7 空氣彈簧橫向剛度 N/mm
4.2 最大水平位移下的外觀
根據TB/T 2841—2010標準中的最大水平位移要求及前文空氣彈簧水平位移計算,在不大于0.7AW0載荷工況下對空氣彈簧施加±125 mm水平位移進行最大水平位移試驗[9-10]。試驗后,空氣彈簧外觀無異常,氣囊表面無打褶、脫層及龜裂等現象。
4.3 載荷內壓
在最大載荷工況(120 kN)下,空氣彈簧的內壓小于650 kPa,滿足設計要求。
4.4 車輛性能驗證
根據實際產品橫向剛度150 N/mm、垂向剛度478 N/mm進行平穩性計算驗證,橫向平穩性指標為2.35,垂向平穩性指標為2.65,滿足設計要求。
永磁直驅轉向架設置有抗側滾扭桿裝置,空氣彈簧剛度對車輛限界影響較小,由于篇幅有限,本文不作具體說明。
5 結論
本文基于永磁直驅車輛服役條件和結構參數,通過幾何分析提出了空氣彈簧變形量計算校核方法,通過仿真計算提出了空氣彈簧懸掛剛度的參數范圍,從而構建了空氣彈簧設計方法。經過對車輛系統進行蛇行運動穩定性、曲線通過性能和運行平穩性動力學計算分析,以及對最終產品進行型式試驗驗證,結果表明,采用本文構建的設計方法所研發生產的空氣彈簧,可以滿足永磁直驅城軌車輛的需求。

