多致動器軸承預緊力加載控制仿真

陳云鵬，楊 芳,2*，馬喜強，李濟順,2，李明巖

(1.河南科技大學 機電工程學院，洛陽 471003；2.河南科技大學 河南省機械設計及傳動系統重點實驗室，洛陽 471003)

0 引言

機床主軸軸承作為主軸工作中的重要部分，其性能很大程度上影響機床整體工作效果[1]。隨著機床加工精度要求的不斷提升，機床主軸軸承則需要在各種工況下，保證精度的同時保持高性能運行。傳統的軸承性能試驗是根據不同軸承的結構特點，以力學、振動、接觸等性能測試為主[2]。但實際工程應用中機床主軸軸承所承受的軸向預緊力，尤其是變載荷運行時，與傳統性能試驗中的要求存在一定差距。因此需根據軸承實際工況的施加高精度的軸向預緊力，從而使軸承試驗最大程度的還原服役狀態下軸承的受力情況，實現對實際工況的模擬。

對于軸承預緊力的實施方式主要有：定量預緊、可調預緊、可變預緊[3]。軸承預緊力作為對軸承性能產生重要影響的因素，隨著預緊力的變化，軸承的剛度也會隨之變化，在保證軸承剛度的情況下，軸承的最佳預緊力在不同轉速情況下也會發生一定變化[4]，適當的預緊力對主軸的回轉性能也會產生一定影響[5]。由此可見，可調預緊力可以有效的提高軸承和主軸工作性能。本文所選用H7006C軸承預緊力范圍為：180N～220N，載荷較小，通過液壓加載[6]的方式難以實現精確可調加載。電磁加載技術對小載荷的施加可以達到很好的效果，但傳統的電磁加載[7]與壓電陶瓷加載[8]由于磁化以及不適用于長時間工作加載，不能產生很好的效果。基于Kim[9]所提出的一種磁致伸縮預緊機構，為減小部件的熱膨脹現象，采用多個致動器對試驗軸承施加載荷，使得每個致動器的輸入電壓減小，有效減小每個致動器所產生的歐姆熱，同時每個致動器直接與軸承內（外）圈相抵接，減小了機構的復雜程度。

本文基于多個致動器沿周向均勻的分布，實現多種載荷加載。各致動器上配有力傳感器，對輸出力值進行監測及反饋形成閉環。基于偏差耦合控制結構，通過模糊PID完成對結構內的各通道輸出力的控制，利用基于擴張狀態觀測器（extended state observer，ESO）的比例-積分控制器對對產生的同步誤差進行實時觀測與處理，將處理過的同步誤差補償到通道中，完成同步誤差補償。仿真結果表明軸向預緊力加載機構可以實現對軸向力的精確可調加載。

1 多致動器力輸出模型

本文以致動器作為執行機構，如圖1所示為致動器的結構示意圖[10]。該裝置通過輸入電流生成驅動磁場，利用磁致伸縮效應，使磁致伸縮材料（Giant Magnetostrictive Material，GMM）[11]產生形變，從而對被驅動物體產生位移，實現力的輸出。

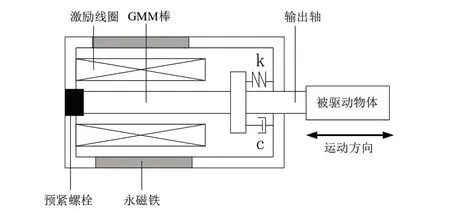
圖1 致動器結構示意圖

根據文獻[12]中的動力學模型建立方法將致動器的動力學過程進行簡化，進而得到等效單自由度的力學模型，如圖2所示，其中各項參數如表1所示。

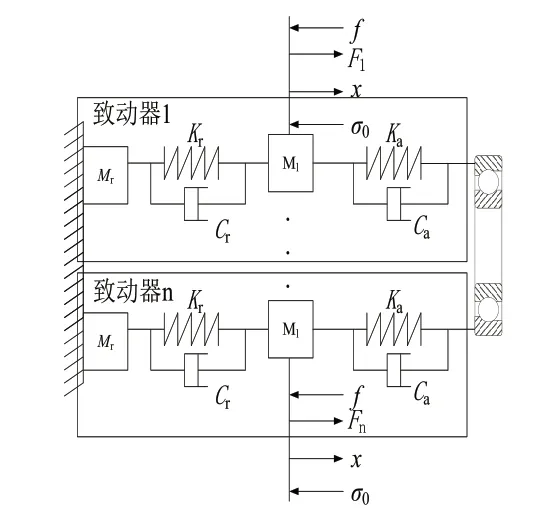
圖2 多致動器等效力學模型

考慮溫度、應力、伸縮棒的質量、阻尼以及磁場引起的磁滯非線性的影響下，基于伸縮棒特性的非線性壓磁方程式為：

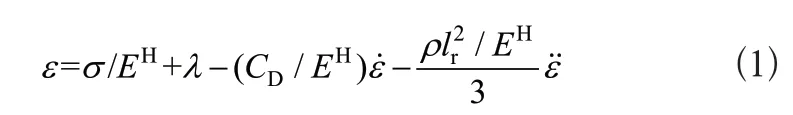
式中ε為伸縮棒長度方向總應變量；EH為伸縮棒的楊氏模量；σ為應力；λ為各向同行材料的磁致伸縮；CD為內部阻尼系數；ρ為質量密度；lr為棒長度。

在整個磁致伸縮運動過程中，負載對伸縮棒的作用力為：

同時伸縮棒一直受到預壓力σ0作用，考慮伸縮棒的質量與阻尼，且根據牛頓第二定律，伸縮棒的輸出力Fi=-(Fa+σ0Ar)即：

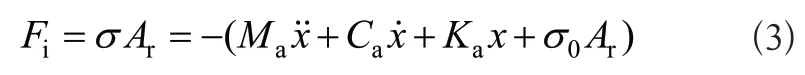
由應變ε=x/lr、式(1)與式(3)聯立可得致動器的動力學方程為：

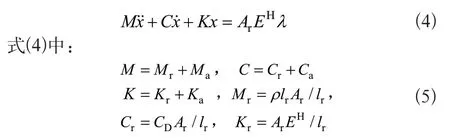
對通過拉氏變換，將式(4)變換為致動器的位移傳遞函數：

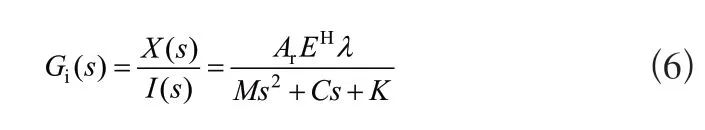
式(6)中，s為算子，X(s)、I(s)分別為位移與電流。

位移驅動負載，則輸出力與位移之間得傳遞函數為：

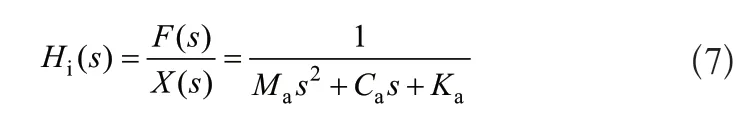
所以單個致動器的輸出力與輸入電流之間的傳遞函數為：

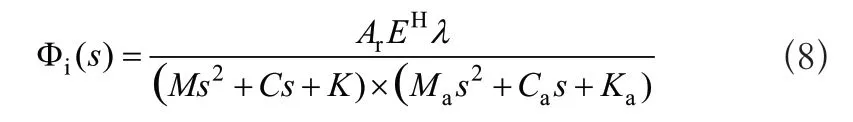
根據圖2所示，軸承外圈所受預緊力F為各致動器輸出力之和，同時選用致動器型號相同，即：

式(9)中，n表示致動器個數。

2 預緊力控制方法

2.1 控制系統結構

本文選用三個致動器作為執行機構，為保證控制精度，所以采用如圖3、4所示的偏差耦合控制結構[13]，該結構主要由多致動器系統、同步誤差補償器以及力控制器組成。力控制器選用模糊PID控制器，在各通道對致動器進行控制，并形成電流-力閉環系統，提高系統的控制精度；同步誤差補償器收集各通道輸出力與輸出力平均值的差，通過基于ESO的比例-積分處理后的值傳遞到通道內，實現對同步誤差的補償；多致動器系統每個致動器都選用相同型號，即每個致動器的傳遞函數相同。

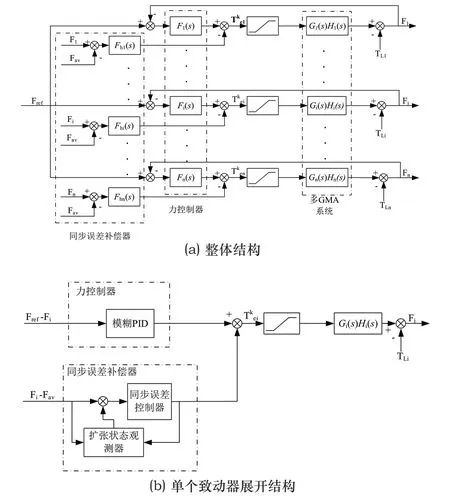
圖3 預緊力控制系統結構

2.2 同步誤差補償器設計

設加載系統的三個致動器分別為H1、H2、H3，每個致動器輸出力與平均輸出力的差為fe，則根據同步控制方案，軸向預緊力加載系統的動態模型為：

式(11)中：ωpi分別為各子系統的外部擾動，將上式中的力同步誤差模型進行轉化，得到二階模型：

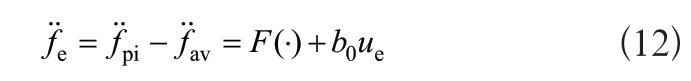
式(12)中：F(·)=(ypi,ypav,upi,upav,)為系統的內、外部未知總擾動的函數，ypi、ypav分別為各系統輸出平均值關于內、外部擾動的函數，b0為可調參數。

假設F(·)可微，令，則對系統的狀態方程的描述如下：

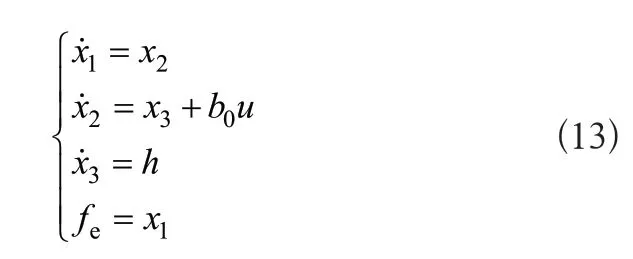
式(13)中u為控制器產生的系統控制量。

針對式(11)所述系統設計ESO[14]：

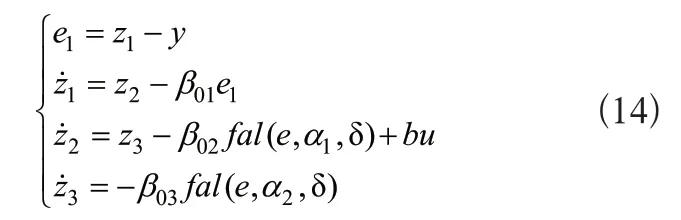
式(14)中：z1、z2、z3分別為系統狀態1、x2、x3的觀測值；通過適當的觀測器的增益參數β01、β02、β03，實現對系統狀態的實時跟蹤；α1、α2分別取1/2、1/4；通過函數fal對信號的抖動進行抑制，函數具體如式(15)所示：

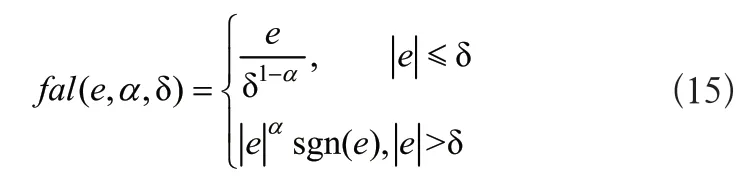
式(15)中δ＞0且代表區間長度。觀測誤差e對函數fla產生增益的大小有較大影響，e的值越大函數產生增益變小，反之越高。

可得基于擴張觀測器的同步誤差控制規律為：

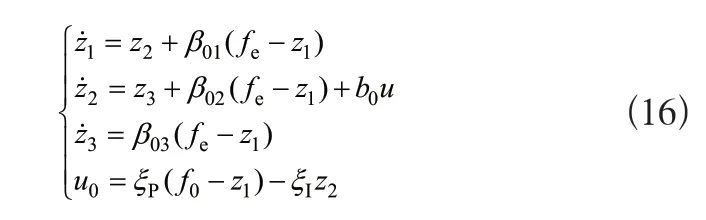
式(16)中ξP、ξI為控制器所需參數，f0為同步誤差的參考輸入。

2.3 控制器設計

本文采用模糊PID控制，控制器結構如圖4所示。系統輸入為誤差E與誤差的變化率EC，輸出為PID參數KP、KI、KD。

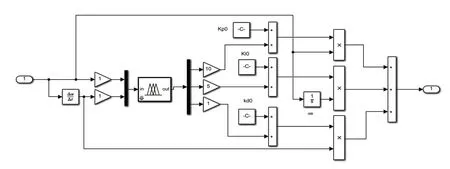
圖4 模糊PID框圖

設輸入E與EC的論域均為(-3,3)，輸出各參數的論域均為(-60,60)，各變量隸屬度函數如圖6所示。規定E與EC的模糊集為{NB，NM，NS，ZO，PS，PM，PB}，則參數KP、KI、KD的模糊集為{NB，NM，NS，ZO，PS，PM，PB}，三個參數的模糊規則如表1～表3所示。

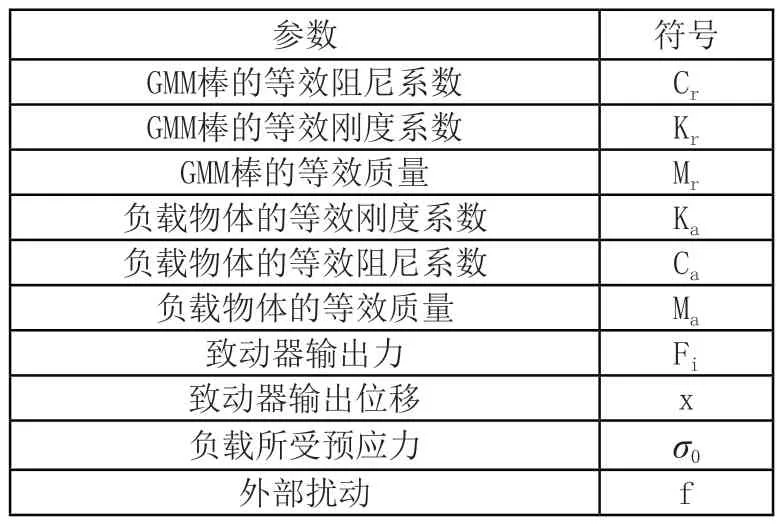
表1 等效模型各項參數

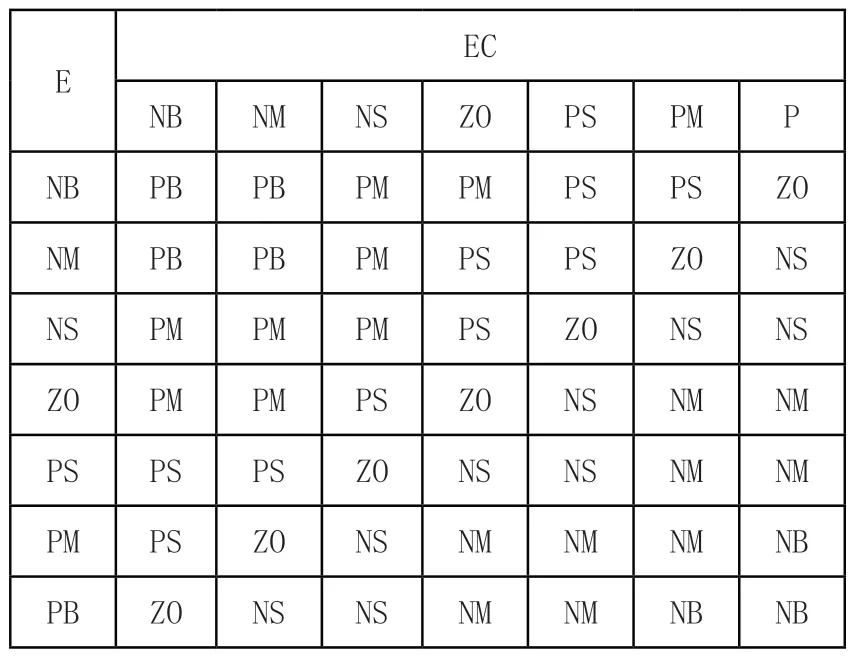
表2 KP模糊規則

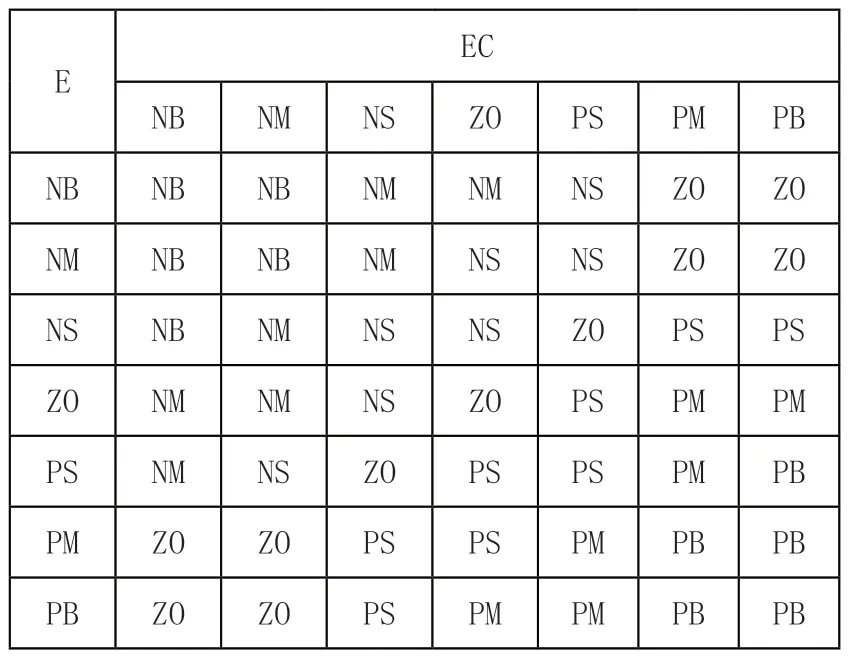
表3 KI模糊規則

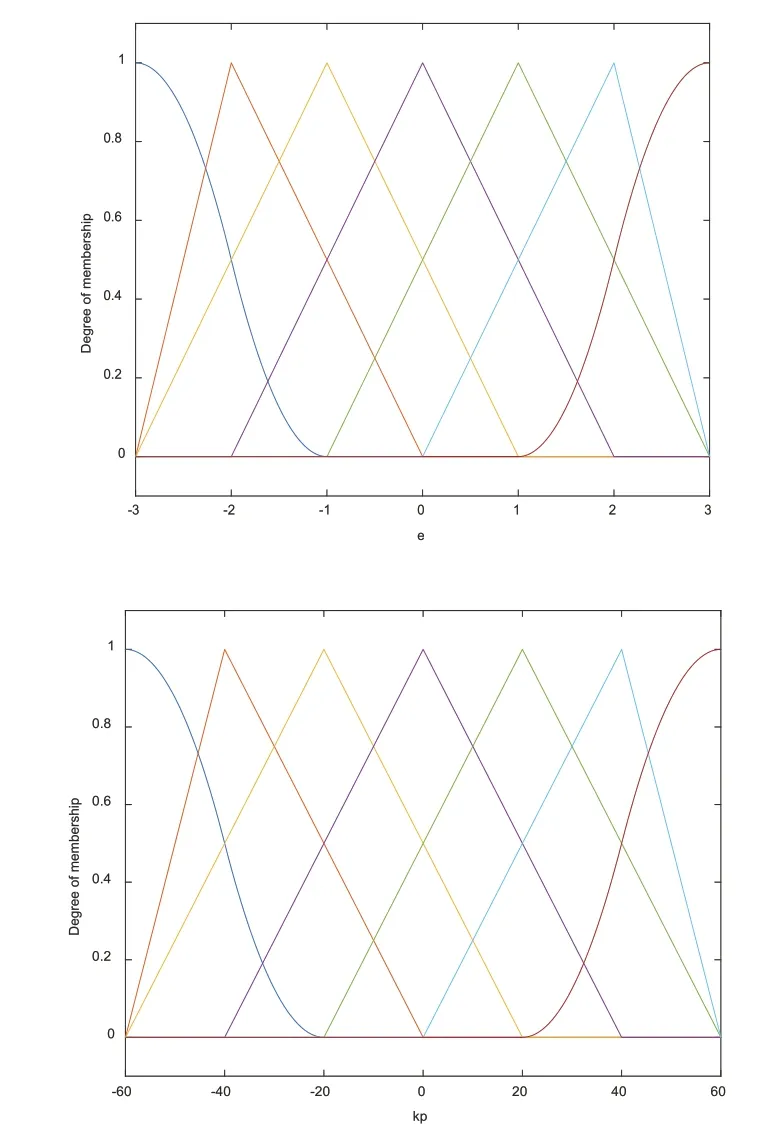
圖5 各變量隸屬度函數

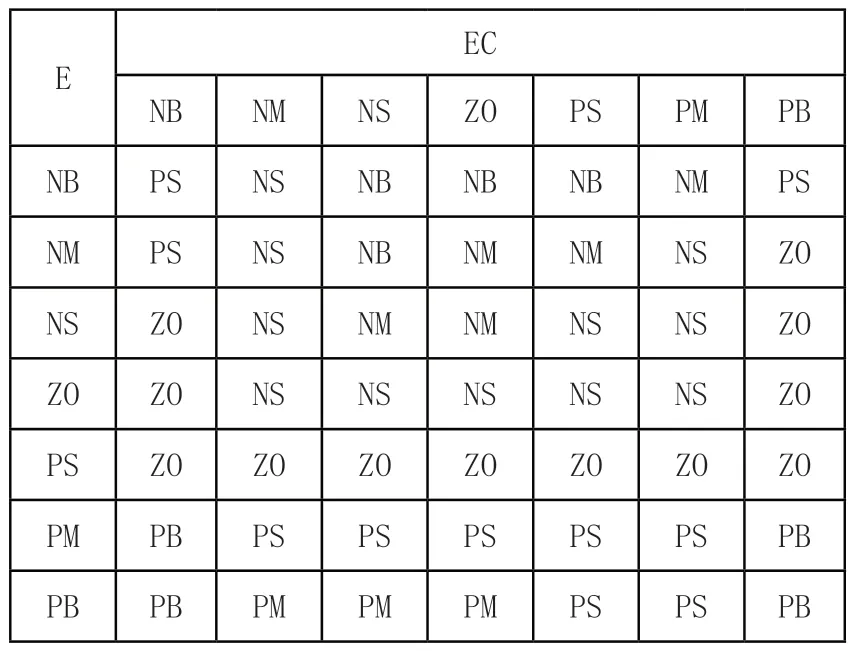
表4 KD模糊規則

3 仿真分析

通過MATLAB/Simulink環境中搭建模型，驗證控制方案的有效性。致動器模型的相關參數[15]如表1所示，對式(8)的傳遞函數進行計算。

試驗要求載荷在180N～300N之間，響應時間不超過1s，控制精度±10%。為驗證所采用的擴張觀測器及模糊PID控制器效果，分別將ESO與模糊PID逐個取出，并與原模型進行對比。上述擴張觀測器的仿真參數設計為β1=30，β2=300，β3=1000，δ=0.01，b0=150；模糊PID中KP、KI、KD三個參數分別設定為41000、387468及1047；同步誤差補償器中的PI控制器參數與子系統中模糊PID的參數存在一定比例關系，分別為HP×KP及HI×KI。為模擬實際工作情況，根據角接觸軸承的振動特性及實際工作中的不確定性[16]，在模型中加入適當頻率、大小的白噪聲對未知干擾進行模擬。

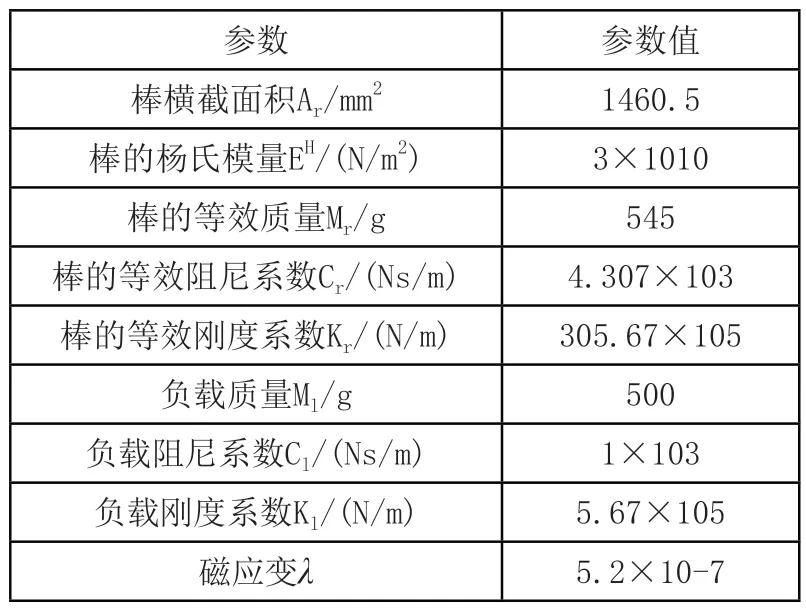
表5 模型相關參數

依照載荷要求范圍，選取180N進行靜力加載仿真，并與傳統PID偏差耦合進行對比，仿真結果如圖6所示。

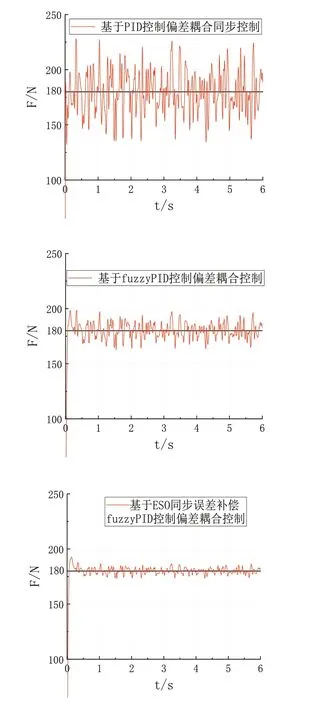
圖6 設定180N時三種控制方法對比

圖6中，軸向加載力目標值為180N，通過基于傳統PID控制器的偏差耦合、基于模糊PID的偏差耦合與本文所采用的基于ESO同步誤差補償器模糊PID控制器的偏差耦合進行對比，可以明顯看出本文所用方法在進入穩態之后，在相同白噪聲的影響下，穩定性明顯優于其他兩種方法。將所獲得數據通過處理得到三種控制方法的均方根誤差分別為42.69277、26.43721及22.46，可知本文所采用控制方法的離散程度更小。由此可見本文所采用控制方法在靜態加載中可以滿足加載需求。

由于本系統采用三個致動器，在每臺致動器上分別施加大小不同的白噪聲作為擾動信號，將第2、3臺致動器的輸出力值進行對比，可以得到第2、3臺致動器之間的同步誤差。在三種控制結構上的每個通道加載相同的擾動，可以得到如圖7所示同步誤差對比，顯然，本文所采用的方法的同步誤差更小、調整速度更快，可見本文所采用控制方法可以等好的減小同步誤差，保持多個執行機構的之間的同步性能。

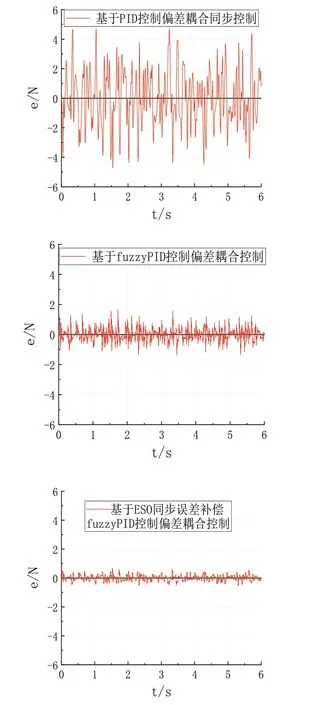
圖7 設定值為180N時三種方法第2、3臺致動器同步誤差

如圖8所示，同步誤差補償器中的HP、HI對系統的同步誤差峰值及調整時間有著較大影響，各子系統之間的最大同步誤差隨著HP、HI增大而減小，但是相應的調節時間卻隨著HP的提高而增大，由圖可知當HP/HI為某一較小比值時，即HP=4，HI=1.5時效果較為優異。

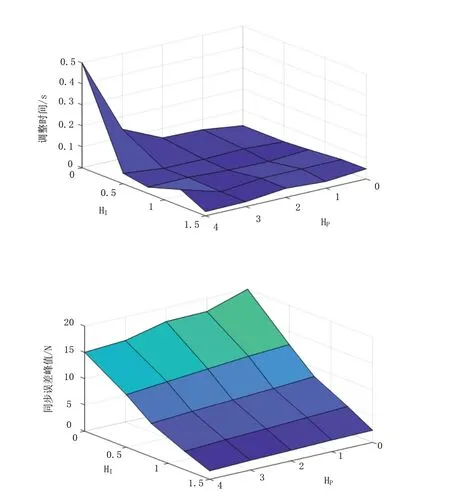
圖8 HP、HI對同步效果的影響

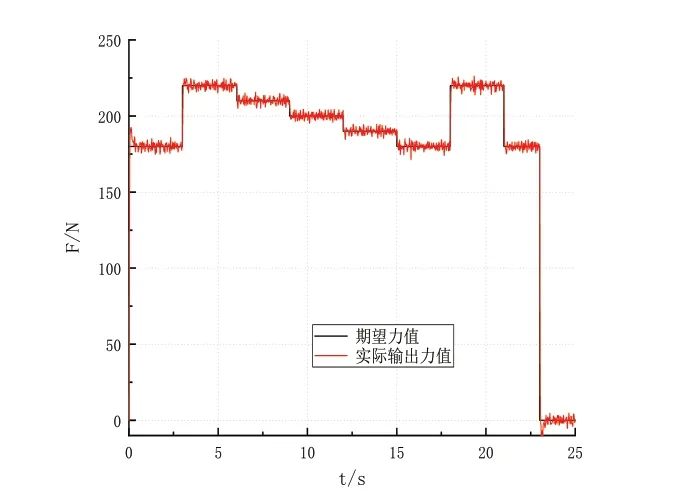
圖9 動態加載仿真

軸承在試驗過程中需要按照選定的載荷譜進行動態試驗，選取載荷譜中的一部分進行軸向預緊力加載裝置的仿真試驗，仿真結果如圖10所示。可以看出相對于靜態加載在動態加載過程中，軸向力的超調量會變大，在穩定狀態下的震蕩幅度與靜態加載時相同，始終保持在允許振蕩范圍內，可以看出軸向預緊力加載控制效果良好。

4 結語

針對機床主軸軸承性能試驗中對預緊力的小載荷、高精度需求，利用多個致動器制定了力控制器，形成以下結論：

1）各子系統內通過模糊PID控制，使PID參數發生改變，顯著的減小了系統的響應時間與超調量。

2）在同步誤差補償器中，通過基于ESO的PI控制器對同步誤差進行處理，減小各子系統之間的同步誤差，提高了各致動器之間的同步性能。

3）根據仿真結果，利用白噪聲對軸承工作狀態的未知擾動進行模擬，對預緊力控制精度產生了影響，但依舊滿足被控對象的高精度要求。