提高函數模型意識,凸顯數學本質屬性
——一道大小比較的探究
雷建榮
(甘肅省慶陽市環(huán)縣第一中學,甘肅慶陽,745700)
1 問題呈現
問題(2022年廣東省佛山市普通高中高三教學質量檢測(二)數學試卷·12)(多選題)已知0 ( ) A. sinx C. cosx+cosy>0 D. cosx+cosy<0 此題以指數函數、三角函數為問題背景構建雙參數方程,以多選題形式設置,判斷三角函數值的大小關系問題.此題設置的主要目的就是考查函數的基本性質,極值點偏移等相關問題.題目難度較大,以廣東省佛山市統(tǒng)考順德區(qū)的11 949名學生的實際得分情況分析,平均得分1.867 3(全佛山市統(tǒng)考學生的平均得分為1.918),難度系數大約是38%左右. 此題的題目設計不夠嚴密,可通過將條件進行簡單變形利用不等式的性質即可求解,其次也可利用特殊值等思想選出部分選項,因而有必要進行進一步的變式與拓展.學生主要是對該題的所處的位置有一定的恐懼心理,沒有深入思考,導致不必要的丟分. 方法1:(同構法1) 解析:由eysinx=exsiny,可得e-xsinx=e-ysiny. 同構函數f(t)=e-tsint,0 結合誘導公式可得e-ysiny=e-xsinx=e-xsin(π-x)>eπ-xsin(π-x),則有x 故選項C正確,選項D錯誤; 故選擇答案:AC. 解后反思:根據題目條件的代數關系式的恒等變形,巧妙同構函數,利用函數的求導處理并確定函數的單調性,通過對應函數的單調性,并結合三角函數的基本性質綜合相關的三角函數公式來分析與解決.同構函數,確定單調性,是大小比較問題中最常用的一種基本方法,關鍵是合理的恒等變形,巧妙同構函數,借助導數確定單調性,為進一步的應用提供條件. 方法2:(同構法2) 故選擇答案:AC. 解后反思:根據題目條件的代數關系式的恒等變形,從另一層面巧妙同構函數,同樣利用導數及其應用,綜合函數的單調性、三角函數的圖象與性質以及三角函數公式等來應用與變形,實現三角函數值大小的比較問題.不同視角的代數式的變形,對應同構的函數也是不同的,思維方式相同,技巧策略相似. 方法3:(放縮法1) 解析:因為x 由0 故選擇答案:AC. 解后反思:根據不等式的基本性質,綜合指數函數的圖象與性質,三角函數的基本性質等進行合理的放縮變形處理,巧妙實現等量關系向不等關系的化歸與轉化,處理起來更加簡單快捷,對數學知識與數學能力等的要求更高.等量與不等量之間的變形與轉化,關鍵是借助函數與方程、函數的圖象與性質等加以巧妙放縮與變形處理,也是解決大小比較問題中比較常用的基本技巧方法,要加以熟悉掌握. 方法4:(放縮法1) 由于0 由于0 那么cos2x-cos2y=(cosx-cosy)(cosx+cosy)>0. 結合0 故選擇答案:AC. 解后反思:根據關系式的恒等變形,合理放縮,結合指數函數的單調性以及方程關系來判斷兩正弦函數值的大小關系,進而利用三角函數的相關公式與基本性質,通過作差比較法以及不等式的性質來進一步判斷兩余弦函數值的大小關系.抓住指數函數與三角函數的基本性質,合理放縮變形,是解決問題的關鍵,也是直擊問題本質,巧妙快捷處理與分析問題的要害. 探究1:原問題設置中所給選項A和B,選項C和D均為對立狀態(tài),必有兩個成立,若從特殊值等情況出發(fā),失去壓軸題的價值,進一步提升可變形為以下變式問題. 變式1(多選題)已知0 ( ) A. sinx C. cosx+cosy>0 D. sinx-cosy>0 解析:因為x 又由0 故選擇答案:ACD. 解后反思:通過改變選項中的相關不等式,以不對立狀態(tài)的選項內容出現,提升知識點與難度,使得問題得以進一步的升華.具體解決問題時,要更深入挖掘題目內涵與實質,剖析相關函數的基本性質,結合函數與導數的綜合來分析與處理. 解決此類大小比較問題,關鍵就是選取合適的函數模型,深入研究函數問題,通過同構函數,借助函數的基本性質來化歸;通過放縮不等式,借助函數單調性來轉化等,不斷積累解題經驗,提高函數模型意識,借助函數的圖象與性質加以數形結合,凸顯數學本質屬性,簡捷有效處理相應的數學問題.2 問題剖析
3 問題破解
3.1 同構思維
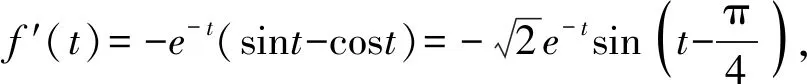
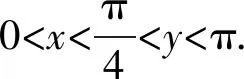

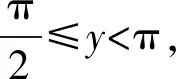
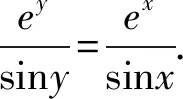
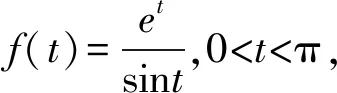
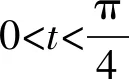
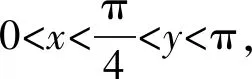
3.2 放縮思維
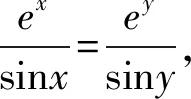
4 變式拓展
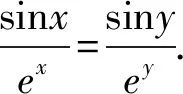
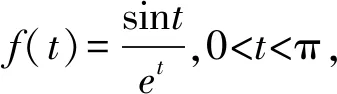
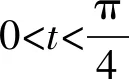
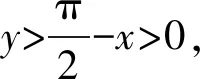
5 教學啟示

