永磁式電磁阻尼器磁性能解析計算及阻尼特性分析

梁仕民,楊國來,李加浩,王麗群,張弘毅

(1.南京理工大學 機械工程學院,江蘇 南京 210094;2.中國計量大學 機電工程學院,浙江 杭州 310018;3.湖南大學 土木工程學院,湖南 長沙 410082)

液壓式制退機具有結構復雜、維護困難和易出現液體泄漏等問題,而電磁阻尼器具有結構簡單、非接觸式和無污染等優點,因此,將電磁阻尼器應用在火炮反后坐裝置中具有重要的工程意義。根據初級激勵源不同,電磁阻尼器主要分為電勵磁式、混合勵磁式和永磁式,電勵磁式和混合勵磁在強沖擊載荷下需要外部電源進行供電,具有體積大、結構復雜和效率低等缺點,不適合火炮反后坐裝置的可靠性和輕量化要求,而永磁式電磁阻尼器不需要額外供電與線圈繞組,具有體積小、可靠性高等優點,在強沖擊載荷下能夠滿足火炮的后坐阻力和后坐位移要求。Halbach永磁陣列具有良好的自屏蔽性能且用少量的磁體就能產生較強的磁場,將該永磁陣列應用于電磁阻尼器中能夠解決永磁體一側漏磁問題。李啟坤等通過有限元仿真軟件分析在強沖擊載荷下Halbach電渦流阻尼器的動力學特性及永磁體發生同軸偏差時對渦流阻尼力的影響情況,但缺少對模型準確性驗證。

分層理論法能較準確地計算出永磁式電磁阻尼器的磁場,揭示電磁阻尼器性能與電磁阻尼器參數之間的聯系。KOU等提出了一種永磁式直線電渦流制動器,利用分層理論推導了電渦流制動器的解析模型,并采用有限元法對制動力特性進行了分析。尹相睿推導永磁直線渦流制動器的磁場分布及力特性方程,并分析其端部效應對磁場和渦流的影響。LI等利用分層理論對高加速度下平板型電渦流阻尼器的制動力進行計算,分析準靜態和高加速度條件下阻尼力的變化規律。文獻[7-9]對平板型電磁阻尼器磁場特性進行了分析,但未分析邊界效應對磁場的影響,而圓筒型阻尼器能量利用率更高,不存在橫向邊界效應影響。CHEN等提出了一款圓筒型磁阻尼器用于解決力傳感器振動問題,利用能量法和等效偽剛體模型對電渦流阻尼器進行動力學分析,同時建立計算磁場分布和阻尼系數的解析模型,其模型分為導體、氣隙和永磁體3個區域,未考慮其余區域對磁場帶來的影響。相較于CHEN等提出的結構,本文采用的圓筒型永磁式電磁阻尼器在充分考慮磁場分布與溫度擴散的影響下存在6個子域,分別為運動導桿域、隔熱層域、永磁體域、氣隙域、導體內筒域與外筒背鐵域。其中外筒背鐵域用于提供磁場的外回路,提高了源磁場的利用率;運動導桿域將磁場的內回路考慮其中;隔熱層避免了身管傳熱對永磁體磁性能帶來的影響。

本文采用圓筒型Halbach永磁式電磁阻尼器方案,通過分層理論將其按結構劃分每個區域,根據不同區域的磁場關系推導出內筒區域的磁感應強度和后坐過程中產生的電磁阻尼力。建立電磁阻尼器有限元模型,與解析模型互相印證。引入火炮后坐運動方程,計算在強沖擊載荷時電磁阻尼器的阻尼特性,并通過有限元分析考慮磁性飽和情況下電磁阻尼力隨內筒厚度的變化規律。

1 Halbach永磁陣列電磁阻尼器模型建立與分析

1.1 圓筒型永磁式電磁阻尼器

永磁式電磁阻尼器主要由外筒背鐵、導體內筒、隔熱層、永磁體和運動導桿等組成,其結構簡圖如圖1 所示。

圖1 圓筒型永磁式電磁阻尼器局部視圖

圖1所示阻尼器的工作原理為當火炮發射發生后坐運動時,運動導桿、隔熱層和永磁體產生主磁場作為初級,內筒和外筒作為次級,當初級和次級發生相對運動時,由楞次定律可知,次級產生渦流從而產生電磁力阻礙初級的相對運動。

1.2 分層理論解析模型建立

應用分層理論求解磁場的電磁性能時,將解析模型分為6個求解區域,以為旋轉軸線的圓柱體剖面簡圖如圖2所示,圖中區域Ⅲ為Halbach永磁陣列,箭頭方向為永磁體的充磁方向。

圖2 分層理論解析求解區域

為簡化分析求解過程,做如下假設:

①模型在方向無限長;只存在環繞導體內筒的渦流,且不考慮渦流產生的趨膚效應。

②氣隙磁感應強度在方向上為恒定值,不計端部效應。

③導體內筒及永磁體的相對磁導率為1。

由麥克斯韋方程組可得:

(1)

(2)

式中:為磁場強度,為電流密度,為磁通量密度,為電場強度。

由磁場本構關系可得:

=

(3)

電流密度:

=σ

(4)

式中:為空氣磁導率;為相對磁導率;內筒導體的電導率=387×10S/m。

當內筒與外筒結合且一起以速度運動時,導體內筒會產生渦流,得:

=(+×)

(5)

(6)

由式(1)、式(3)和式(6)推導可知:

(7)

為了簡化計算,將4個不同充磁方向的永磁體作為一個整體,由傅里葉級數可得磁矢勢的表達式為

(8)

式中:=π,電磁阻尼器極距=+;徑向充磁方向永磁體長度=20mm;軸向充磁方向永磁體長度=15mm。

因為區域Ⅰ、Ⅱ、Ⅳ、Ⅵ的電導率為0,由式(7)可知:

(9)

式中:代表Ⅰ,Ⅱ,Ⅳ,Ⅵ。

對于區域Ⅲ永磁體陣列區域,永磁體的本構關系用剩余磁通密度來表示:

=+

(10)

式中:為永磁體剩磁,大小為145 T,剩磁在和方向分別為徑向剩磁和軸向剩磁。

=res,+res,

(11)

由式(1)、式(7)、式(10)和式(11)可得:

(12)

在區域Ⅴ處,由于導體內筒的電導率不為0,導體內筒以速度運動,則由洛倫磁力可得:

(13)

右邊的左側項為感生電動勢,右側項為動生電動勢,在計算運動情況下不計及感生電動勢,因此式(13)可表示為

(14)

由拉普拉斯算子在圓柱坐標系下的表示法得每個區域的解析式為

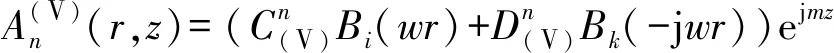
式中:和是由邊界條件確定的常數,和為不同類別貝塞爾函數,為非齊次貝塞爾方程解。在相鄰區域的邊界上,磁通密度的法向分量是連續的,磁場強度的切向分量是連續的。

設=745 mm,=1345 mm,=1375 mm,=1670 mm,=1690 mm,=1705 mm。

在法向的邊界條件,即1=2:

在切向上的邊界條件,即1=2:

式中:運動導桿導磁系數、隔熱層導磁系數和背鐵導磁系數均為600。

通過對磁矢勢的求解,可以得到內筒導體內的磁通密度和渦流分布:

由高斯定理可求得柱坐標下矢量場在不同坐標系中旋度的表達式:

由上述公式可求內筒處軸向電磁阻力:

1.3 有限元模型建立

為了驗證解析模型的準確性,建立圓筒型Halbach永磁陣列電磁阻尼器的有限元模型,如圖3所示,圖中自下而上分別是空氣域、運動導桿、隔熱層、永磁體、氣隙、導體內筒、外筒背鐵和空氣域。電磁阻尼器的結構是由多個旋轉體組成,為簡化計算,選用二維軸對稱的計算模式進行分析。由于永磁陣列在軸向的長度是有限的,為了消除端部效應對結果的影響,有限元模型計算的結果選自永磁陣列處中間一個周期進行分析,本構關系的選擇與解析模型一致。

圖3 有限元仿真模型

在有限元法中,瞬態磁場仿真可以求解非恒定磁場中初級與次級的相對運動情況,通過賦予內外筒一個穩定增長的速度,觀察初級與次級發生相對運動時電磁阻尼器的變化情況,計算磁感應強度和電磁阻尼力。

1.4 模型驗證

對導體內筒(=(-)2)處的磁感應強度隨軸不同位置的變化規律分別進行了有限元和解析求解,對比結果如圖4所示。在速度為0時,磁感應強度曲線在徑向充磁方向的永磁體處呈現出平緩的曲線,但在速度為12 m/s時,由于渦流去磁的作用使得平緩的曲線變為一個極值,從2種方法的結果對比可以看出吻合效果較好。

圖4 導體內筒處徑向磁感應強度與位置曲線

后坐阻力和速度之間的關系如圖5所示。可以看出,解析模型的解與有限元模型解變化規律一致,且最大誤差為5.47%,在可接受范圍內,由此可得當速度增加到一定值時,電磁阻尼力的增加不再隨速度的增加而增加,此時所對應的速度值稱為臨界速度值,當后坐速度超過臨界速度值時,電磁阻尼力會隨著速度的增加而減小,因此在設計電磁阻尼器時,應確保后坐速度不會超過臨界速度值,否則會在火炮后坐過程中造成不可避免的損壞。

圖5 后坐阻力與后坐速度的關系

2 強沖擊載荷下阻尼特性分析

2.1 電磁阻尼器的后坐運動分析

引入火炮的后坐運動方程,編寫某大口徑火炮炮膛合力載荷激勵函數和根據火炮的復進要求選定復進機的類型,后坐過程中炮膛合力曲線和復進機的后坐行程函數曲線如圖6和圖7所示。

圖6 炮膛合力曲線

圖7 復進機力曲線

將上述曲線作為電磁阻尼器的激勵函數,得到電磁阻尼器在強沖擊載荷下后坐運動過程響應,如圖8所示。從圖8中可以看出,在后坐位移到達100 mm左右時,后坐速度處于最高速度,約為12.4 m/s,同時電磁阻尼力也達到峰值,整個后坐行程約為740.5 mm。由圖5可知,在強沖擊載荷的后坐過程中,其最大后坐速度未超過臨界速度。

圖8 強沖擊載荷下后坐運動過程響應

在強沖擊載荷作用下,電磁阻尼器產生的阻尼力如圖9所示,產生的電磁阻尼力峰值約為530 kN,有限元與解析法產生的結果最大誤差為2.59%,整個后坐過程時間約為150 ms。

圖9 電磁阻尼力有限元法與解析法對比

2.2 不同結構參數對電磁阻尼力的影響

當電磁阻尼器設計完成后,其能夠承受的最大阻尼力、臨界速度等也隨之確定。因此在設計電磁阻尼器前,需要研究不同結構參數對電磁力的影響規律。

由于空氣中的磁阻遠大于內筒,所以不同的氣隙寬度對電磁阻尼力的影響均不同。電磁阻尼力隨氣隙寬度的變化規律如圖10所示。可知,當內筒與永磁體之間的氣隙越小,產生的電磁阻尼力也會越大,且后坐運動所需要的時間也越短;氣隙越大,電磁阻尼力越小,后坐運動所需要時間越多。在理想情況下,雖然氣隙寬度越小,其產生的阻力也會隨之增加。但是,氣隙寬度減小會同時增加加工難度并影響散熱,因此,在設計時應綜合各種因素合理選擇氣隙寬度。

圖10 電磁阻尼力隨氣隙寬度變化規律

在解析法中考慮磁性飽和情況非常困難,為確保有限元仿真結果更貼近實際,在有限元仿真中考慮背鐵的磁性飽和情況,即背鐵磁化強度達到某一值時,外磁場強度增強而磁化強度不再增加。從圖11可知電磁阻尼力隨內筒厚度的變化規律,在一定范圍內,當內筒的厚度增加時,內筒感應出的電渦流面積也隨之增加,使得產生的電磁阻尼力增加,隨著渦流面積的增加,電渦流產生的磁感應強度增加,渦流產生的磁感應強度與永磁體產生的磁感應強度方向相反,導致磁場中的磁感應強度也隨之減少,從而產生退磁現象,電磁阻尼力曲線呈現出“馬鞍”型。

圖11 電磁阻尼力隨內筒厚度變化規律

當內筒厚度較小時并不會出現退磁現象,電磁阻尼力呈現出較為平穩的趨勢,但當內筒厚度過小時,渦流面積較小,其產生的電磁阻尼力不能滿足后坐需求,故合理選擇內筒厚度能夠避免退磁現象和電磁阻尼力不足的情況。

3 結束語

利用分層理論推導了磁場的表達式,建立了Halbach永磁陣列電磁阻尼器的解析模型,同時建立有限元分析模型,并進行了互相印證。通過有限元法分析不同的氣隙寬度和內筒厚度對電磁阻尼力的變化規律,為電磁阻尼器的設計提供一定的理論參考。但解析模型缺少對磁性飽和、導體內筒溫度發生變化而引起阻尼變化的影響,在后續工作中應進一步研究。