亞音速飛行器往復式滑翔增程彈道設計

王璟慧,姜 毅,楊昌志,2

(1.北京理工大學 宇航學院,北京 100081;2.中國運載火箭技術研究院 戰術武器總體技術部,北京 100076)

射程是巡航導彈有效攻擊目標的關鍵因素,是衡量巡航導彈系統作戰能力的一個重要指標。為滿足當前遠距離、精確化、大威力的現代戰爭作戰要求,增程技術是巡航導彈技術重點發展方向之一。決定射程的因素有動力系統、飛行器外形、飛行姿態控制、飛行彈道設計等方面。目前各國采用的增程方法主要有優化外形減阻增程、發動機助推增程、滑翔增程以及復合增程等。

針對亞音速巡航導彈的增程問題,國外學者致力于通過提高發動機工作效率、優化導彈外形結構等方式來提高巡航導彈射程。美國在亞音速隱身巡航導彈“聯合空地防區外導彈”(JASSM)基礎上,通過換裝渦扇發動機增大推力,降低油耗實現武器增程,同時研發新型彈翼,實現導彈射程的大幅提升,研制了“增程型聯合空地防區外導彈”(JASSM-ER)。俄羅斯采用核動力取代常規動力形式,發展新型核動力巡航導彈,擁有無限續航能力,提高其遠程精確打擊能力。然而,考慮彈體結構及發動機制造工藝水平等因素限制,通過這2種方法增加射程仍存在一定局限性。基于已有學者提出的新型亞音速往復式滑翔盤旋延時彈道方案,本文提出一種針對亞音速巡航導彈的往復式滑翔增程彈道方案,導彈在豎直平面內做下降、上升的往復運動,整個過程中其速度、高度、推力等不斷發生變化,發動機僅在上升階段工作。

飛行器滑翔飛行最大的優勢是可以不依靠自身動力而借助氣動力實現自身的運動。對于飛行器滑翔彈道的研究,SANGER提出一種名為“Silverbird”的助推-跳躍式概念飛行器;錢學森提出一種利用空氣動力進行滑翔增程的“錢學森彈道”。滑翔增程彈道方案通過調整舵翼偏轉來控制飛行器升力,使飛行器緩慢下降,延長飛行時間進而達到增程目的。在利用滑翔方式實現增程的研究方面,符蓓蓓等研究滑翔增程的原理及彈道特性,建立超遠程制導炮彈滑翔增程外彈道數學模型,對最大升阻比彈道進行仿真;修觀等研究在給定射程條件下的火箭助推滑翔增程彈最短飛行時間彈道優化問題;張斌等針對火箭彈增程問題,提出以攻角為優化變量,利用改進單純形優化算法最優控制理論對滑翔增程進行分析;史金光等研究對比俯仰滑翔飛行與旋轉滑翔飛行2種運動模式對彈箭增程效率的影響;此外,史金光等還對鴨式舵面進行氣動設計以保證有效增程;凌王輝等針對彈道導彈進行減阻設計實現增程。綜上所述,對于亞音速巡航導彈增程問題的研究主要在提高發動機工作效率、優化導彈外形結構,這2種方法研制周期長,技術方案存在一定局限性;對于滑翔增程彈道方案的研究主要集中在火箭彈、炮彈等領域,將滑翔方式應用于亞音速巡航導彈增程問題的研究相對較少。因此,對于利用滑翔方式提高亞音速巡航導彈航程的研究十分必要。

為提高亞音速巡航導彈的航程,本文提出一種往復式滑翔的巡航彈道方案,建立水平直飛巡航彈道與往復式滑翔巡航彈道模型,對比2種彈道方案的有效航程,分析往復式滑翔巡航彈道的增程效率與彈道特性,在此基礎上研究初始飛行馬赫數、初始彈道傾角和初始飛行高度對增程效率的影響,為增大亞音速巡航導彈航程的相關研究和工程應用提供一定的理論指導。

1 模型建立

1.1 計算流體模型

本文的研究對象參考美國“戰斧”巡航導彈。圖1為“戰斧”巡航導彈,圖2為本研究中使用的三維模型示意圖。

圖1 “戰斧”巡航導彈

圖2 三維模型示意圖

楊昌志等通過對比三維翼型RAE2822氣動參數的數值計算結果與風洞試驗結果,驗證了數值風洞仿真方法的有效性與可靠性。基于數值風洞仿真方法,求解了飛行器升力系數和阻力系數等氣動參數。上述飛行器模型的氣動參數表如下,表1為升力系數()表,表2為阻力系數()表。表中,為攻角,為馬赫數。基于二維插值方法,可以得到不同馬赫數和不同攻角下飛行器的升力系數和阻力系數。

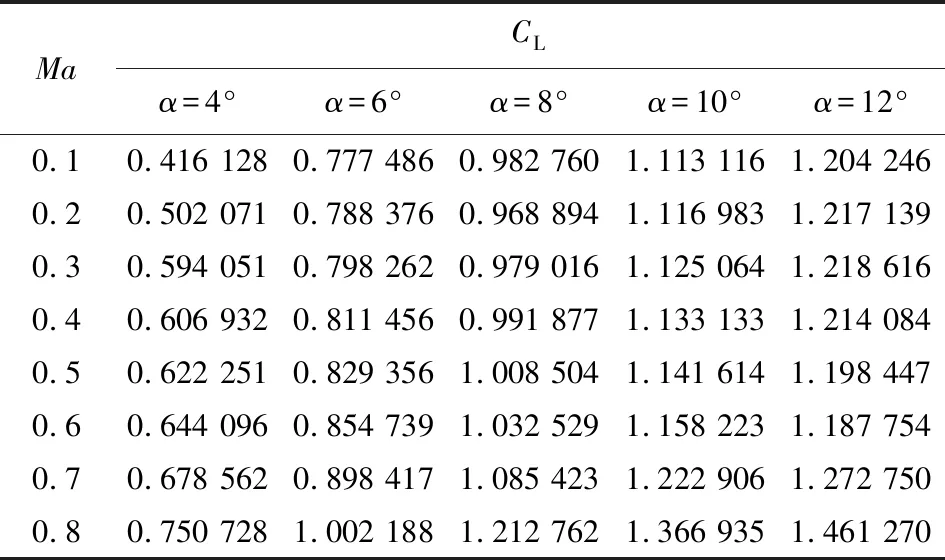
表1 升力系數表

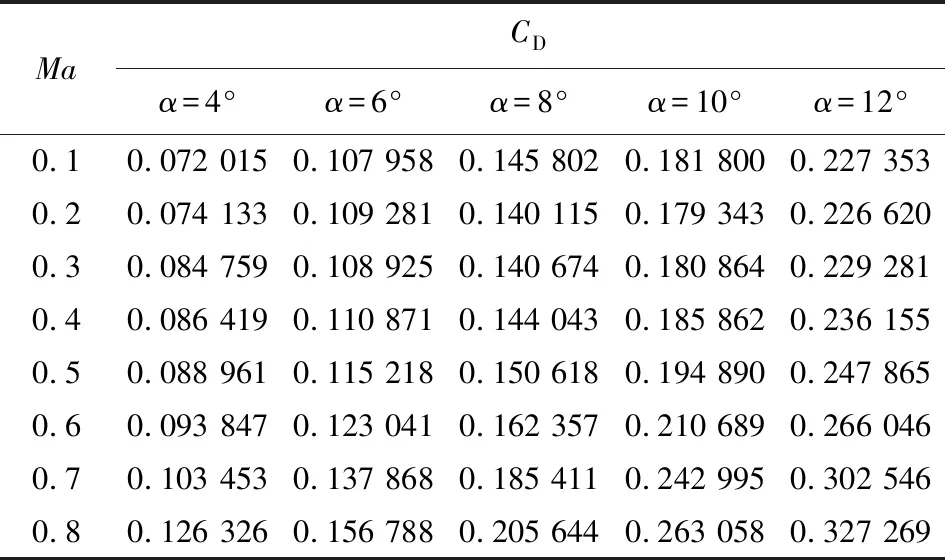
表2 阻力系數表

1.2 彈道模型

為研究往復式滑翔彈道的增程效率,本文基于導彈模型與其氣動數據,構建導彈巡航階段常規的水平直飛彈道與借助滑翔的往復式滑翔增程彈道2種飛行彈道模型。為抓住問題的主要方面,本文假定導彈的縱向對稱面始終與飛行平面重合,探測系統和控制系統的作用是理想的,地球表面為平面。本研究中飛行距離指飛行平面內導彈從初始位置到燃油耗盡位置的水平位移。一定條件下導彈的彈道設計相關參數如表3所示。

表3 彈道設計相關參數

1.2.1 水平直飛彈道

水平直飛彈道為巡航導彈的常規巡航彈道,其彈道特點是導彈不做大的機動飛行,為等高等速飛行。要使得該過程中導彈的速度與高度保持不變,導彈自身重力、發動機推力、氣動升力與氣動阻力必須始終平衡。由于這一過程發動機一直處于工作狀態,導彈總質量不斷變化。為保證等高等速飛行,導彈攻角及推力會發生相應改變。水平直飛彈道方程為

式中:為導彈推力;為攻角;、分別為導彈受到的氣動升力和氣動阻力;為導彈質量;,分別為飛行器的阻力系數、升力系數,基于表1、表2的氣動數據,由導彈不同速度和攻角插值得到;為動壓;為飛行器特征面積;為當地大氣密度;為飛行器速度;為導彈所在高度重力加速度;地表重力加速度=9.81 m/s;地球半徑=6 371 km;為飛行器距地表高度;為發動機耗油率;為導彈的二維平面水平位移。

1.2.2 往復式滑翔增程彈道

往復式滑翔增程彈道的特點是導彈在豎直平面內做下降、上升的往復運動,在整個過程中其速度、高度、推力等不斷發生變化。每一次往復運動分為4個階段,依次分別為:①無動力滑翔下降階段,②無動力下降-上升轉彎階段,③動力助推上升階段,④無動力上升-下降轉彎階段。這4個階段為1個飛行周期。往復式滑翔彈道示意圖如圖3所示。

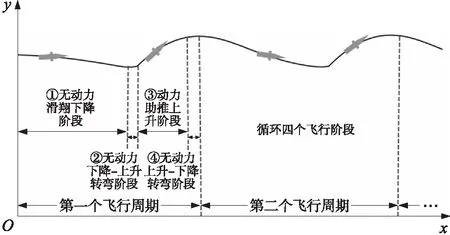
圖3 往復式滑翔彈道示意圖

往復式滑翔增程彈道的具體飛行過程如下:導彈爬升至某一高度進入巡航階段時,具有一定的初始速度與彈道傾角,之后導彈開始進入無動力滑翔下降階段。該過程中導彈發動機處于關機狀態,僅依靠飛行器所受氣動力和自身重力的調節來實現無動力滑翔下降。依據導彈氣動力參數,擬合最大升阻比下的攻角隨馬赫數的變化曲線,采用最大升阻比攻角方案實現無動力滑翔下降階段的滑翔增程。當導彈無動力滑翔下降至臨界高度后進入無動力下降-上升轉彎階段。在無動力下降-上升轉彎階段發動機仍處于關機狀態,導彈通過調整氣動舵翼改變飛行姿態使導彈產生向上的加速度,實現下降-爬升的轉彎效果。當導彈轉彎上升到距地面200 m的臨界高度后進入動力助推上升階段,該過程中為保證導彈繼續上升,發動機開始工作。為提高發動機的使用效率,發動機推力大小由當前時刻導彈的速度、彈道傾角以及飛行高度等參數共同調節,當導彈需加速爬升時,發動機推力增大,當速度足夠大時,發動機推力減小,此過程中發動機推力最大值為10 kN。當導彈上升至進入巡航段的初始高度后,發動機關閉進入無動力上升-下降轉彎階段。該階段與無動力下降-上升轉彎階段類似,導彈通過調整氣動舵翼改變飛行姿態,使導彈產生向下的加速度,使彈體實現爬升-下降的轉彎,當導彈的縱向速度變為0時,則進入下一次往復運動的無動力滑翔下降階段。如此往復運動直至導彈巡航段結束。

往復式滑翔彈道方程為

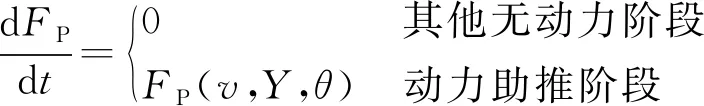
式中:,分別為導彈的水平分速度和豎直分速度;為彈道傾角;,分別為導彈的水平位移和豎直位移。

水平直飛彈道的特點是導彈飛行高度與速度保持不變,發動機一直處于工作狀態;往復式滑翔增程彈道的特點是導彈做滑翔下降、助推上升的周期性往復運動,發動機僅在助推爬升段工作。圖4為2種飛行彈道的軌跡對比示意圖。

圖4 兩種飛行彈道軌跡對比示意圖

1.3 數值方法

彈道微分方程的求解采用4階精度的Adams預估-校正法,該方法迭代計算量少,計算速度快,效果較為理想。具體算法如下。

設有一階微分方程:

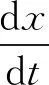
Adams預估-校正法的遞推計算公式如下:

預估公式為

校正公式為

利用Adams預估-校正方法進行數值積分,求解+1時要求已知,-1,-2,-3時刻的(,)值。因此一般采用Runge-Kutta方法啟動,算出前四步的積分結果,再利用Adams預估-校正方法進行迭代計算。相比于Runge-Kutta法每積分一步需要計算4次函數值,Adams預估-校正法啟動后每積分一步只需要計算兩次函數值,計算量更少。

2 仿真結果與分析

以上文中建立的彈道模型為基礎,結合一定條件下導彈的彈道設計相關參數,可以計算得到不同工況下水平直飛彈道與往復式滑翔彈道的飛行距離,對比研究往復式滑翔彈道的增程效率以及導彈初始飛行馬赫數、初始彈道傾角、初始飛行高度對往復式滑翔彈道增程效果的影響。

2.1 往復式滑翔彈道增程效率研究

通過對比分析不同工況下導彈水平直飛彈道和往復式滑翔彈道的飛行距離,研究往復式滑翔彈道的增程效率,計算工況如表4所示。對于往復式滑翔彈道,選擇初始飛行馬赫數作為變量,分別為0.55,0.6,0.65,0.7,0.8,0.9,初始彈道傾角均為-2°;對于水平直飛彈道,初始飛行馬赫數為0.55,初始彈道傾角為0°。兩種彈道的初始飛行高度均為1 000 m。通過數值求解得到兩種彈道的飛行距離。表5為導彈不同工況下兩種彈道的有效航程對比。

表4 兩種彈道的計算工況

表5 不同工況下兩種彈道有效航程對比

從表5中可以看到水平直飛彈道和往復式滑翔彈道的飛行距離差異。在初始飛行高度為1 000 m,初始飛行馬赫數為0.55時的水平直飛彈道飛行距離為298.078 km,本文提出的往復式滑翔彈道在計算工況中飛行距離為552～600 km,增程效率最大可達101.21%。說明往復式滑翔彈道能有效增加導彈飛行距離。為降低計算工況局限性的影響,通過對比不同計算工況下往復式滑翔彈道的飛行距離與水平直飛彈道的最優飛行距離,進一步研究往復式滑翔彈道的增程效果。下面研究水平直飛彈道的最優飛行距離。

導彈受飛行穩定性及舵機等裝置限制,求解飛行距離最大問題的本質為尋優問題。求解導彈飛行距離的最大值等價于求解飛行距離負值的最小值。該問題最優解的求解過程為一維優化問題。一維搜索優化計算方法是指在確定的搜索方向上按步長因子迭代,使得目標函數在該方向上達到極小值的過程。本文使用格點法求解水平直飛彈道最大飛行距離。格點法的求解思路如下。

在設計變量∈[,]區間內部取個等分點:,,…,。各點坐標為

對應各點函數值,,…,。其中,最小值為=min{,,…,},則區間[-1,+1]內必包含極小值,取[-1,+1]為新區間。滿足收斂條件+1--1≤時,最優解→,→。若達不到精度要求,則重復上述步驟,把當前區間作為初始搜索區間,直至滿足精度要求為止。

基于121節中水平直飛彈道公式,本文以飛行速度作為設計變量,其變化區間∈[05,08],以飛行距離最大建立目標函數min(-())。

求()的最大值即為求-()的最小值,可建立目標函數min(-()),利用上述格點法進行求解。取=10,=0000 1,當+1--1≤0000 1時,計算終止。

攻角的取值取決于導彈物理參數及舵機的修正能力,為保證導彈飛行穩定性,約束攻角的變化范圍為≤≤。攻角最小值=1°,攻角最大值=8°。

經迭代計算得到水平直飛彈道中飛行距離最大為299.255 9 km,此時飛行馬赫數為0.5701 1。對比往復式滑翔彈道的飛行距離與水平直飛彈道的最大距離,發現往復式滑翔彈道依然能夠實現增程,增程效率為84.67%～100.42%。水平直飛彈道飛行距離隨飛行速度變化的曲線如圖5所示。從圖5中可以看出,水平直飛彈道的飛行距離隨著飛行速度的增大先增大后減小,這是由飛行速度與飛行時間共同決定的。隨著飛行速度的增大,飛行器單位時間位移增加,但同時飛行器所受阻力也增加,為抵抗阻力,飛行器在單位時間燃油消耗增加,將會導致總體飛行時間變短,因此在飛行速度與飛行時間的共同影響下,飛行距離必然存在極值。

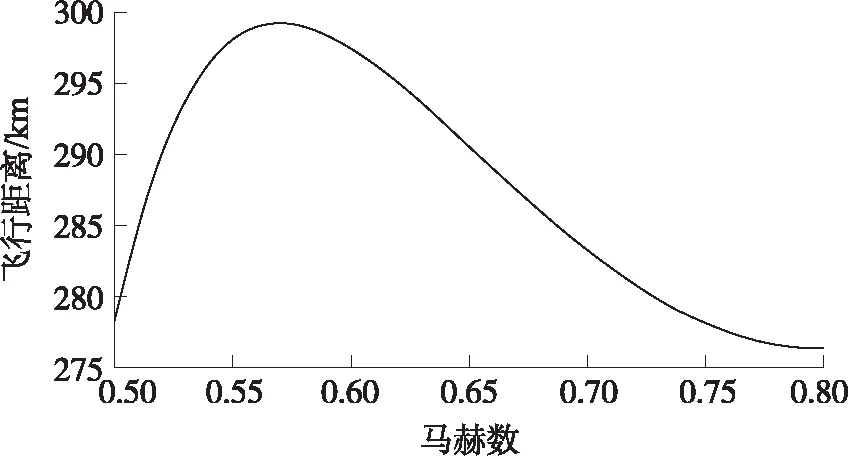
圖5 水平直飛飛行距離隨速度變化

為分析往復式滑翔彈道對增程效果的貢獻原理,從能量守恒角度出發,通過對比兩種飛行彈道在相同導彈參數與初始參數條件下發動機推力做功,進一步研究往復式滑翔彈道的增程原理。

設置兩種彈道的初始飛行馬赫數均為0.6,初始飛行高度均為1 000 m。求解得到兩種彈道的有效航程,水平直飛彈道有效航程為297.462 6 km,往復式滑翔彈道有效航程為572.650 1 km。相比于水平直飛彈道,往復式滑翔彈道的增程效率為92.51%。

往復式滑翔彈道飛行過程的能量守恒方程為

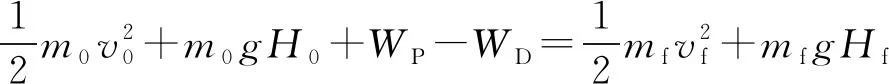
式中:為飛行器初速,為飛行器末速,為飛行器初始質量,為飛行器最終質量,為飛行器初始高度,為飛行器最終高度,為推力做功,為氣動阻力做功。

水平直飛彈道整個過程中能量守恒方程為

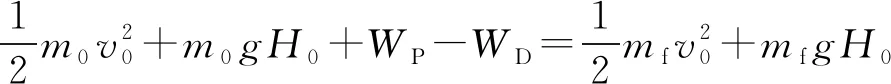
比較兩種彈道在飛行相同的水平距離時發動機推力做功。圖6為兩種飛行彈道推力做功對比,圖7 為兩種飛行彈道燃油質量消耗對比。

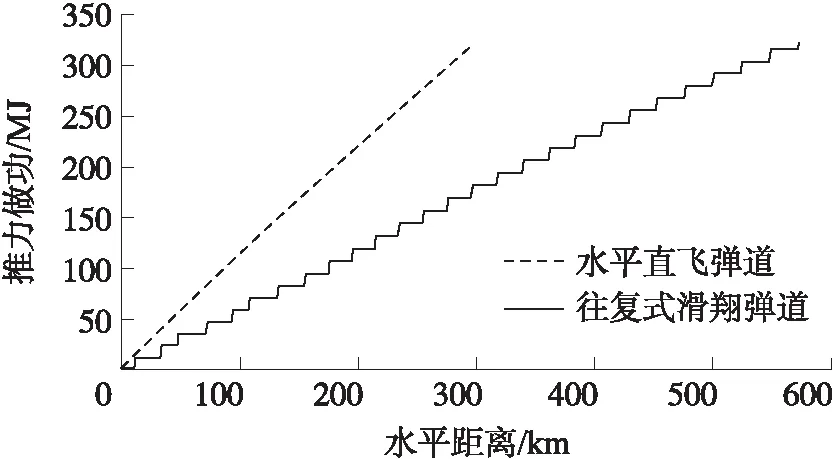
圖6 兩種飛行彈道推力做功對比

圖7 兩種飛行彈道燃油質量消耗對比

對比圖6,由于水平直飛彈道發動機一直處于工作狀態,往復式滑翔增程彈道發動機僅在助推爬升段工作,在飛行相同的水平距離時,水平直飛彈道推力做功大于往復式滑翔彈道推力做功。由圖7可以看出,在相同飛行距離時,相比于往復式滑翔彈道,水平直飛彈道消耗燃料質量更多。綜上,飛行器飛行相同的水平距離時,水平彈道發動機推力做功更多,燃料消耗更多。因此,在相同燃料的條件下,水平直飛彈道的有效航程更小。

2.2 初始飛行參數對往復式滑翔彈道影響分析

在分析了往復式滑翔彈道增程效率的基礎上,研究導彈初始飛行參數對往復式滑翔彈道飛行距離的影響。工況參數基準:初始飛行馬赫數為0.55,0.60,0.65,0.70,0.80,0.90;初始彈道傾角為0,-2°,-4°,-6°,-8°;初始飛行高度為800 m,900 m,1 000 m,1 100 m,1 200 m。

2.2.1 初始飛行馬赫數影響分析

初始飛行馬赫數分別取0.55,0.60,0.65,0.7,0.8,0.9,計算分析不同初始飛行馬赫數對應的飛行能力。不同工況計算時,初始彈道傾角與初始飛行高度分別保持一致,僅改變初始飛行馬赫數。表6為不同初始飛行馬赫數工況的飛行距離;圖8～圖10分別為不同初始飛行馬赫數工況下部分彈道對比、各周期開始滑翔時刻速度對比和累計飛行距離對比。

表6 不同初始飛行馬赫數工況飛行距離

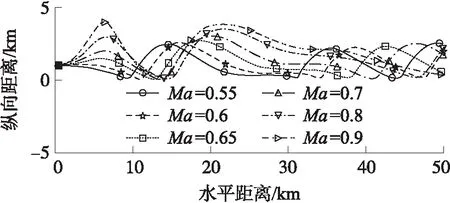
圖8 不同初始飛行馬赫數工況部分彈道對比

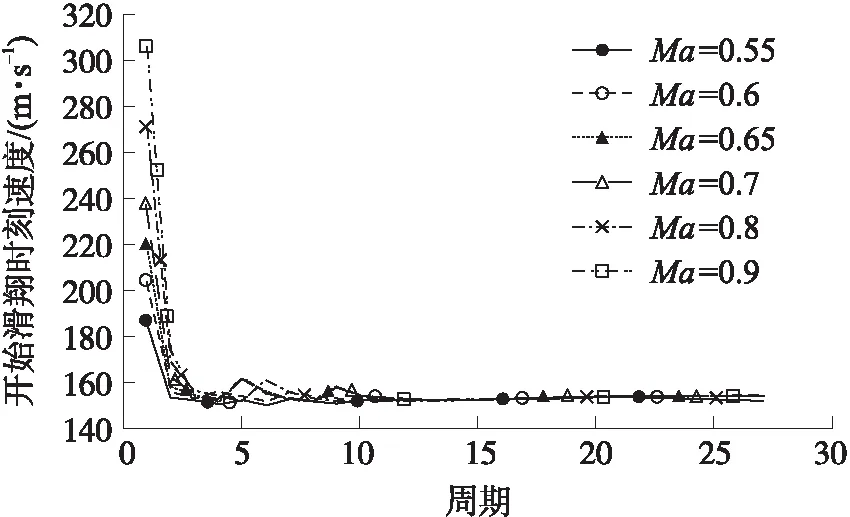
圖9 不同初始飛行馬赫數工況各周期開始滑翔時刻速度對比

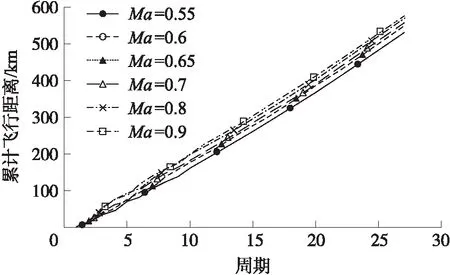
圖10 不同初始飛行馬赫數工況累計飛行距離對比

對比表6中不同初始飛行馬赫數下的飛行距離可得,隨著初始飛行馬赫數的增大,往復式滑翔彈道的飛行距離增大。從圖8局部彈道對比圖可以看出,在飛行初始階段,初始飛行馬赫數越大,初始飛行周期的滑翔距離越長。觀察圖9,前幾個周期開始滑翔的速度均存在上下波動,說明初始飛行周期中導彈的運動狀態受初始飛行馬赫數影響;經過一段飛行時間后,每個周期開始滑翔時刻的速度逐漸趨于一致。這是因為導彈在往復式滑翔過程中,經氣動力和自身重力不斷調整,經過一段時間后不同初始飛行馬赫數工況下的導彈會呈現出相似的運動狀態。圖9中,初始飛行馬赫數越大,導彈每個周期開始滑翔的速度越大,因此每個周期的滑翔距離也會變大,導致了最終飛行距離的增大。圖10中每周期累計飛行距離隨著初始飛行馬赫數的增大而增大證明了這一點。因此,隨著初始飛行馬赫數的增大,每個周期開始滑翔的速度越大,每個周期的滑翔距離越大,往復式滑翔彈道的最終飛行距離也越大。

2.2.2 初始彈道傾角影響分析

初始彈道傾角分別取0°,-2°,-4°,-6°,-8°,計算分析不同初始彈道傾角對應的往復式滑翔彈道性能。初始縱向速度向下時,初始彈道傾角為負,反之為正。在本研究中,初始彈道傾角為非正數,描述初始彈道傾角的變化趨勢時,均采用其絕對值的變化。表7為不同初始彈道傾角工況的飛行距離;圖11～圖14分別為不同初始彈道傾角工況下部分彈道對比、各周期開始滑翔時刻速度對比、各周期飛行距離對比以及各周期燃油質量消耗對比圖。

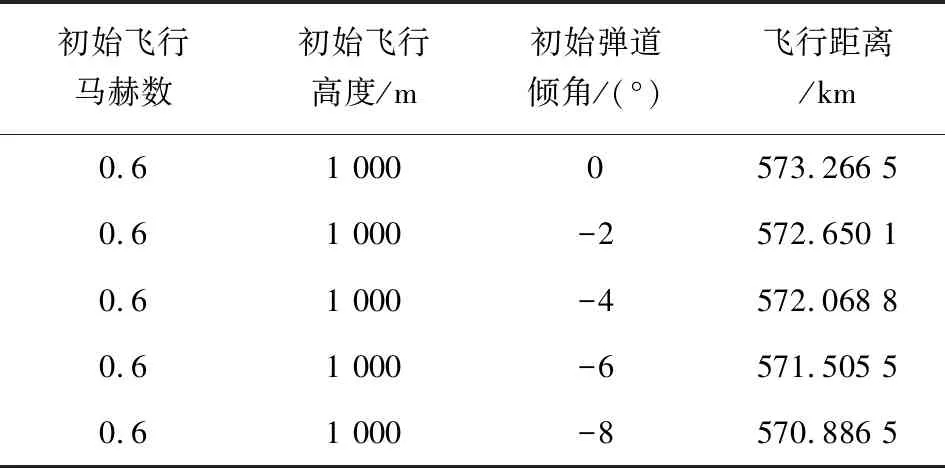
表7 不同初始彈道傾角工況的飛行距離

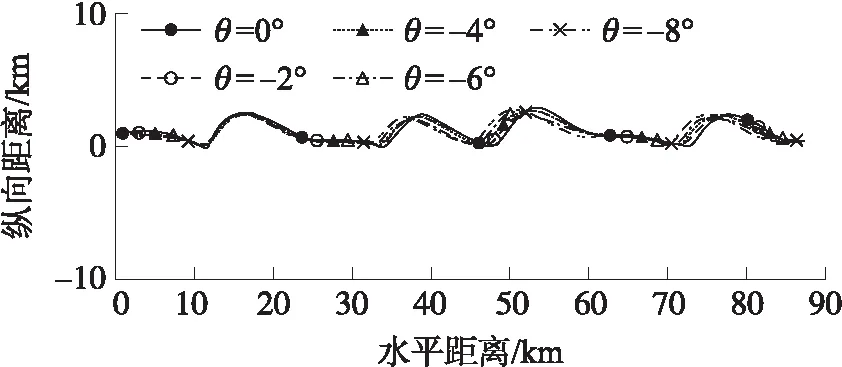
圖11 不同初始彈道傾角工況部分彈道對比

圖12 不同初始彈道傾角工況各周期開始滑翔時刻速度對比

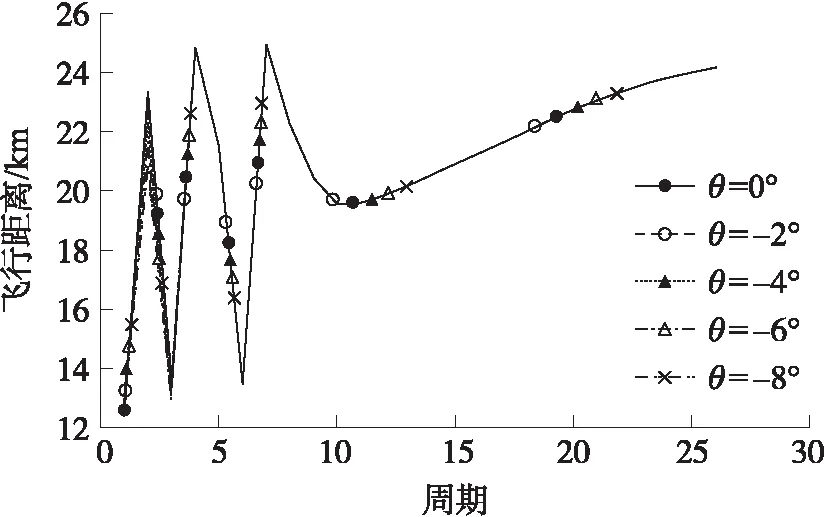
圖13 不同初始彈道傾角工況各周期飛行距離對比

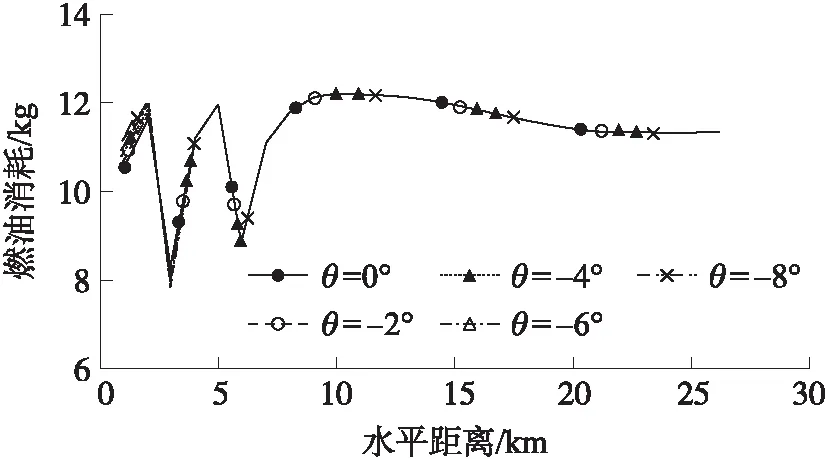
圖14 不同初始彈道傾角工況各周期燃油質量消耗對比

對比表7中不同初始彈道傾角下的飛行距離可得,隨著導彈初始彈道傾角的增大,往復式滑翔彈道的最終飛行距離逐漸減小。從圖11部分彈道對比圖可以看出,在飛行初始階段,初始彈道傾角越小,初始飛行周期的滑翔距離越長。觀察圖12～圖14,初始飛行周期中導彈的運動狀態受初始彈道傾角影響,前幾個周期存在不同程度的波動,經過幾個周期后,不同工況中每個周期開始滑翔時刻的速度、每個周期的飛行距離以及每個周期消耗燃油質量逐漸趨于一致。導彈飛行初始時間段內不同初始彈道傾角工況的彈道差異,導致不同工況導彈最終飛行距離的差異。

從圖12可以看出,初始彈道傾角越小,導彈前幾個周期開始滑翔的速度越大;圖13中可以看出初始彈道傾角越小,前幾個周期中,每個周期飛行的距離也越大;圖14中可以看出初始彈道傾角越小,前幾個周期的燃油消耗質量越少,即相同的燃油質量,初始彈道傾角越小,可以飛行的距離越遠。綜合分析,導彈經歷氣動力與重力的共同調整后,不同初始彈道傾角工況的彈道特性趨于一致,因此初始彈道傾角的影響只存在于初始部分的飛行周期,即不同初始彈道傾角的最終飛行距離取決于初始部分的飛行周期。初始彈道傾角越小,初始部分周期開始滑翔的速度越大,該周期內飛行距離越大并且燃油消耗質量越少,使得往復式滑翔彈道的最終飛行距離隨之增大。

2.2.3 初始飛行高度影響分析

初始飛行高度分別取800 m,900 m,1 000 m,1 100 m,1 200 m,計算分析不同初始飛行高度對應的飛行距離。表8為不同初始飛行高度工況的飛行距離;圖15～圖17分別為不同初始飛行高度工況部分彈道對比、各周期燃油質量消耗對比以及每周期累計飛行距離對比。

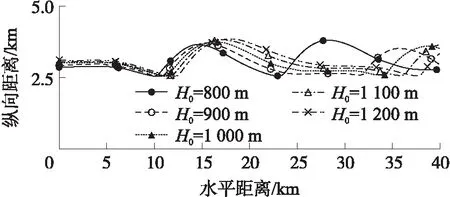
圖15 不同初始飛行高度工況部分彈道對比

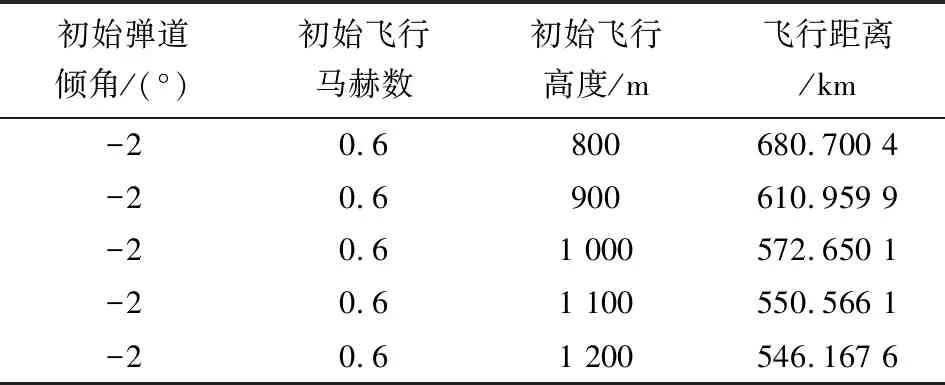
表8 不同初始飛行高度的飛行距離

對比表8中不同初始飛行高度下的飛行距離,可以看出初始飛行高度越低,往復式滑翔彈道的最終飛行距離越大。從圖15的局部彈道對比圖可以看出,初始飛行高度越高,每個飛行周期的滑翔距離越長。但是從結果來看,初始飛行高度越高,最終飛行距離反而更小。從圖16中分析可知,初始飛行高度越高,每個周期燃油質量消耗越大,使得導彈的總體飛行周期變少。由圖17可知,雖然初始飛行高度越高,每個飛行周期的累計飛行距離越長,但是其飛行周期越少,使得總體的飛行距離越小。因此,總體飛行周期變少是導致不同初始飛行高度工況最終飛行距離變短的原因。

圖16 不同初始飛行高度工況各周期燃油質量消耗對比

圖17 不同初始飛行高度工況各周期累計飛行距離對比

研究發現,當初始飛行馬赫數低于0.5、初始彈道傾角大于25°、初始飛行高度低于700 m時,導彈難以完成往復式滑翔彈道,在無動力下降-上升轉彎階段出現飛行高度過低而“觸地”的情況,無法實現增程。導致這一現象的原因均是導彈在進入轉彎階段時縱向速度過大,進入轉彎階段后導彈難以依靠調整自身氣動力的方式實現拉起,最終造成往復式滑翔彈道的失敗。因此,為了保證往復式滑翔彈道的成功與增程效果,在設計該彈道初始飛行參數時,應該結合導彈的具體氣動特性進行選擇。

3 結束語

本文采用一種往復式滑翔增程彈道方案,可有效增大亞音速巡航導彈航程。研究了往復式滑翔彈道相比于常規水平直飛彈道的增程效率以及其彈道特性,分析了初始飛行參數對往復式滑翔彈道增程特性的影響。主要結論如下:

①往復式滑翔彈道能夠有效增加導彈飛行距離。相比于水平直飛彈道的最大飛行距離,往復式滑翔彈道的增程效率達到100.42%。

②初始飛行馬赫數越大,往復式滑翔彈道的增程效率越高;初始彈道傾角越小,增程效率越高。經過多個周期滑翔過程中氣動力與重力的共同調整,不同初始彈道傾角的彈道特性趨于一致,因此不同初始彈道傾角的最終飛行距離取決于初始的飛行周期;初始飛行高度越低,往復式滑翔彈道的有效航程越大。初始飛行高度越低,每個周期燃油質量消耗少使得飛行周期增大。總體飛行周期增加是導致不同初始彈道傾角工況有效航程變長的主要原因。

③應當綜合考慮導彈的氣動特性與彈道特性來設計彈道初始飛行參數,保證往復式滑翔彈道的成功實現與增程效果。

本文對往復式滑翔彈道增程效率以及初始參數對往復式滑翔彈道影響的研究,為亞音速巡航導彈的增程技術提供了一種創新性方案,為相關研究和工程應用提供了一定基礎。