航空發動機套齒連接結構剛度特性仿真分析及試驗研究

李倫緒 陳 果 楊默晗

1.南京航空航天大學民航學院，南京，210016 2.南京航空航天大學通用航空與飛行學院，常州，213300 3.中國航空發動機集團有限公司湖南動力機械研究所，株洲，412002

0 引言

套齒連接結構具有承載能力強、定心和導向性能好、結構緊湊、易于安裝、可靠性高等優點，常應用于現代航空發動機低壓轉子系統中風扇轉子和低壓渦輪轉子的連接[1]。套齒連接存在多個接觸面，花鍵副及圓柱定位面多采取小間隙配合，隨著轉子軸系工作狀態的改變，交變載荷作用于套齒連接結構上，可能使得其連接界面發生滑移、分離等接觸狀態的變化，導致結構整體剛度表現出明顯的非線性變化特征，最終影響轉子系統的動力學特性，甚至可能出現套齒結構連接不穩定而引發的轉子軸系振動加劇。因此，研究套齒連接結構剛度特性及其影響因素對航空發動機低壓轉子系統軸系連接的設計，以及排除轉子系統振動故障等問題具有重要意義。

目前國內外學者針對套齒連接結構剛度特性進行了大量的研究工作。LIU等[2]建立了簡化的低壓轉子套齒連接結構三維實體有限元模型，計算并分析了徑向力、定位面間距、配合間隙量/過盈量以及寬度對套齒連接結構整體線剛度和角剛度的影響規律，結果表明套齒剛度特性隨載荷呈現非線性的變化規律。WU等[3]建立了考慮定位面接觸剛度的套齒連接結構力學模型和某型含套齒連接結構的轉子系統三維實體有限元模型，計算了套齒結構的靜態剛度，并與試驗結果進行了對比，結果表明，局部剛度表現為非線性和不確定性，進而影響轉子系統的動力學特性。朱彬等[4]建立了考慮齒面嚙合和定心面接觸的剛度解析模型，并分析了橫向載荷、扭矩、定心面緊度等對結構等效剛度的影響規律。ZHANG等[5]利用套齒剛度測試裝置進行剛度測試，建立了該套齒試驗器的三維實體有限元模型，計算了徑向力、定位面配合間隙量/過盈量等參數對剛度特性的影響，并與試驗結果進行了對比驗證。HONG等[6]基于半解析套齒載荷分布模型，提出了套齒聯軸器的一般剛度計算公式，并將其用于分析其徑向、角向、扭轉以及耦合剛度參數，研究發現套齒聯軸器載荷分布不均，剛度隨旋轉角度變化呈現非線性特征。CURA等[7]通過理論分析和試驗研究了對中情況和不對中情況下花鍵聯軸器的扭轉剛度，結果表明不對中將使得花鍵聯軸器扭轉剛度減小。李俊慧等[8]建立了套齒連接結構接觸有限元模型，分析了結構參數及載荷對剛度特性和定位面接觸狀態的影響，并提出了針對套齒結構的動力學設計方法。王亭月[9]建立了套齒連接結構有限元模型，分析了橫向剛度和彎曲剛度隨扭矩和橫向力的變化規律，并進行了試驗驗證。李蔚曦[10]建立了三種不同結構形式的套齒連接有限元模型，構建了更為復雜的內外花鏈軸接觸區域，分析了其剛度特征及接觸狀態。CHEN等[11]利用套齒連接結構有限元模型分析了擰緊力矩對連接剛度的影響規律，并進一步討論了擰緊力矩對結構動力學特性的影響。陳曦等[12]提出了新型套齒連接結構的力學模型，通過理論分析和試驗重點研究了軸向螺母擰緊力矩對套齒結構剛度和轉子系統固有特性的影響。蘇志敏等[13]建立了某轉子套齒-拉桿連接結構有限元模型，計算了剛度損失及接觸應變能分布、摩擦功等，并提出優化設計方案，降低了彎曲剛度對載荷的敏感性。許卓[14]建立了某型套齒聯軸器三維有限元模型，分析了軸向剛度和徑向剛度隨載荷的變化規律，并自行設計了套齒連接結構剛度測試裝置進行了靜態剛度測試。蘇鈞聰[15]、趙廣等[16]基于Hertz接觸理論和粗糙表面的彈性接觸模型，建立了航空發動機低壓轉子套齒聯軸器圓柱定位面的接觸剛度模型，并進行了數值仿真和試驗驗證。MARMOL等[17]推導了側面嚙合套齒結構的橫向剛度，并建立了耦合套齒結構的非同步振動數學模型。廖仲坤等[18]推導了套齒聯軸器的嚙合剛度以及動態嚙合力的計算公式，分析了扭矩變化、套齒不對中和動態相對位移變化時套齒的嚙合力和嚙合剛度。

綜上所述，目前國內外學者在套齒連接結構剛度變化規律、等效模型和動力學特性等方面取得了豐碩的研究成果，但針對航空發動機套齒連接結構剛度非線性特征產生機理研究較少，并且套齒連接結構仿真模型中一般忽略齒面接觸，考慮齒面接觸的套齒連接結構整體剛度特性和特征參數影響規律尚需進一步研究。鑒于此，本文建立考慮齒面接觸的套齒連接結構實體有限元模型，進行套齒連接結構靜剛度試驗，從仿真和試驗兩個方面揭示套齒連接結構剛度非線性變化規律及其產生機理，分析關鍵特征參數對剛度特性的影響規律。

1 套齒連接結構剛度特征分析

1.1 套齒連接結構

典型的航空發動機低壓轉子套齒連接結構如圖1所示，主要由含內花鍵的風扇軸、含外花鍵的低壓渦輪軸和鎖緊螺母三部分組成。其中套齒嚙合結構傳遞扭矩，鎖緊螺母施加軸向力實現軸向壓緊，提高結構整體連接的穩定程度，A、B兩個圓柱定位面控制低壓渦輪軸和風扇軸的同軸度，通常情況下，B位置定位面采用間隙配合，風扇軸與低壓渦輪軸之間有一定的配合間隙。

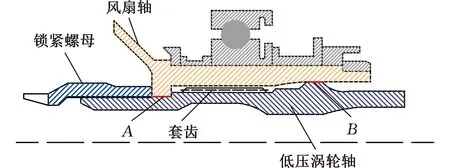
圖1 低壓轉子套齒連接結構Fig.1 Spline coupling of low-pressure rotor

在實際工作環境中，套齒連接結構承受風扇、壓氣機、渦輪等部位的軸向拉壓載荷，同時結構承受不平衡力引起的彎矩和陀螺力矩等多種彎曲載荷，其整體受力特征為大螺母鎖緊承受軸向力，雙圓柱面實現定心并承受剪力和彎矩，套齒嚙合部分主要承受扭矩。由于結構不連續，在受載過程中，套齒連接結構的變形狀態和接觸狀態發生變化，導致其彎曲剛度具有一定的非線性特征。

1.2 剛度非線性特征及其產生機理

在彎矩作用下，套齒連接結構的受力狀態如圖2所示，低壓渦輪軸右側P點承受彎曲載荷M，左側鎖緊螺母施加軸向預緊力Fp實現軸向壓緊，由于套齒連接結構左側和右側分別與風扇轉子和渦輪轉子相連，兩者分別承受向右和向左的軸向氣動載荷，使得風扇軸和渦輪軸在連接面A處壓緊效果良好，接觸狀態基本穩定。連接面B處為間隙配合，如圖中①所示，初始間隙為Δw。在彎矩M的作用下，低壓渦輪軸發生彎曲變形。當低壓渦輪軸連接面B處徑向變形大于初始間隙Δw時，低壓渦輪軸和風扇軸接觸，兩者承受接觸產生的相互作用力FB，如圖中②所示。連接面B受力情況和接觸狀態的改變導致套齒連接結構彎曲剛度具有明顯的非線性特征。

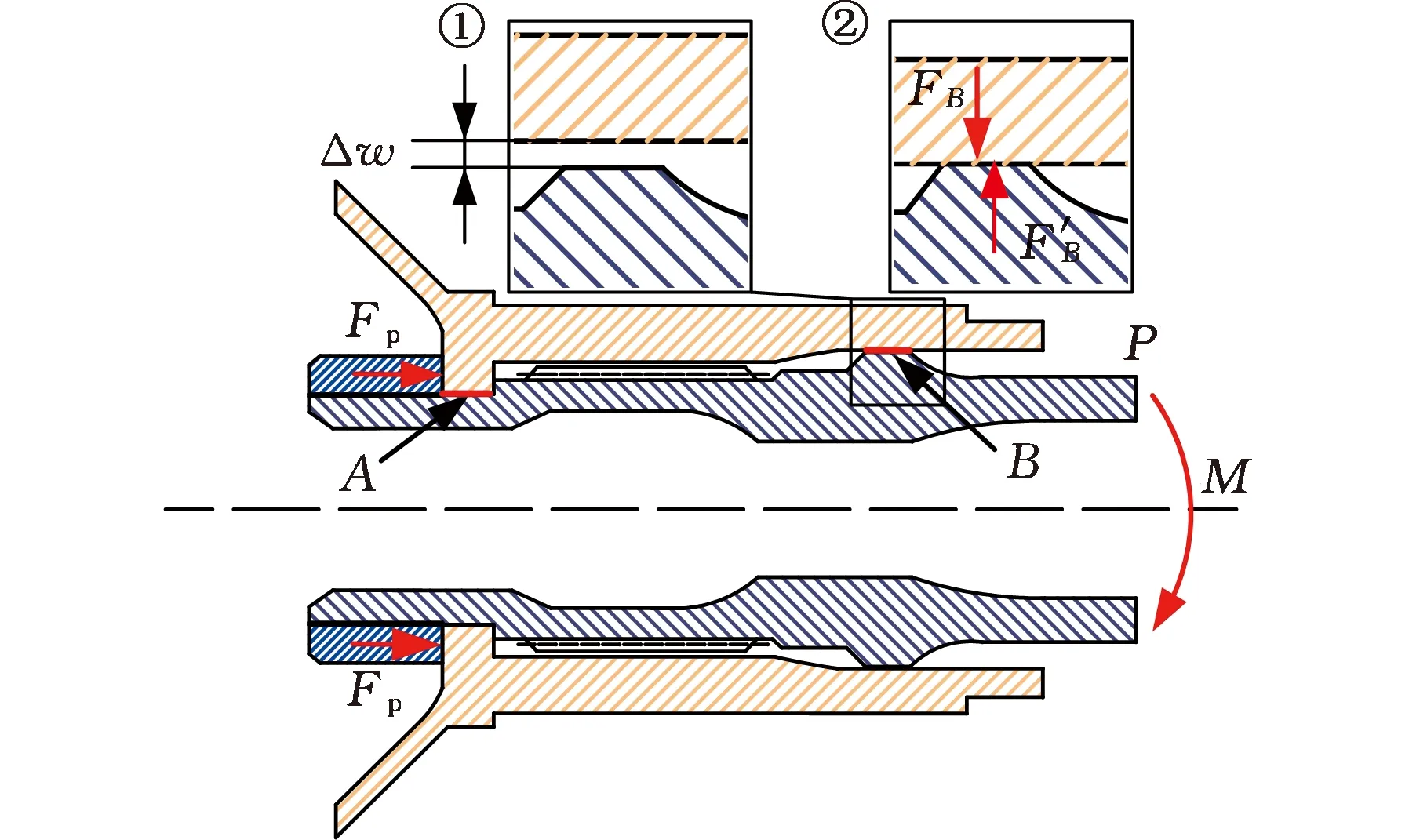
圖2 套齒連接結構受力分析Fig.2 Stress analysis of spline coupling

套齒連接結構在承受端部彎曲載荷后將產生徑向變形和轉角，通過徑向變形和轉角表征的彎曲剛度為線剛度和角剛度，兩者對彎曲剛度的表征效果相同，本文選取線剛度進行彎曲剛度分析。由于連接面A接觸狀態良好，假設低壓渦輪軸和風扇軸在連接面A處徑向位移相同，選取AP段套齒連接結構分析其剛度非線性機理。將結構進行等效簡化，在等效模型中，連接面A和連接面B分別用點a和點b表示，右側端面P用p表示。在彎矩M作用下，根據低壓渦輪軸b點徑向位移w1是否大于初始間隙Δw，即連接面B有無接觸，可以將套齒連接結構的變形狀態分為兩個階段。

(1)第一階段：w1<Δw，即定位面B處于分離狀態。低壓渦輪軸在p點彎曲載荷M作用下類似于懸臂梁結構發生彎曲變形，將其進行等效簡化，如圖3所示，則p點的轉角ωp1可表示為

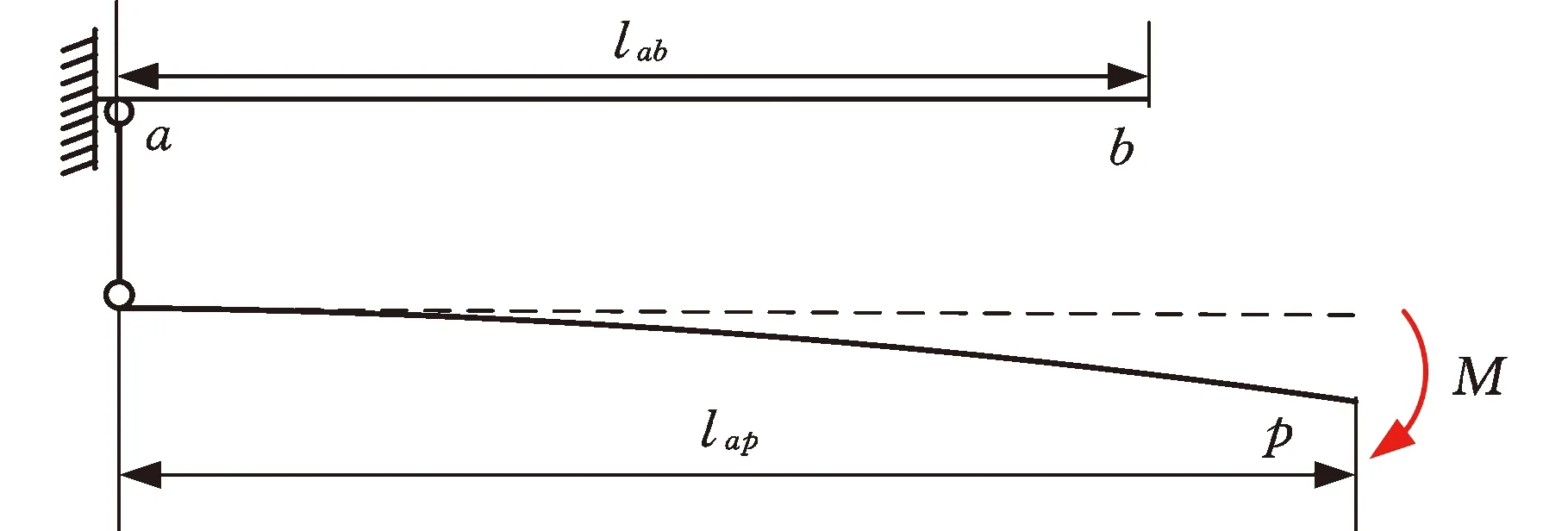
圖3 套齒連接結構等效梁模型(接觸前)Fig.3 Equivalent beam model of spline coupling structure(before contact)

(1)

式中，E1、I1分別為低壓渦輪軸的彈性模量和截面慣性矩；lap為低壓渦輪軸ap段的長度。

(2)第二階段：w1>Δw，即低壓渦輪軸和風扇軸在定位面B處處于接觸狀態。低壓渦輪軸在彎矩載荷M作用下克服初始間隙與風扇軸接觸，將兩者簡化為懸臂梁結構，將低壓渦輪軸和風扇軸在連接面B的接觸等效為剛度為kB的彈簧，則其等效簡化模型如圖4所示，b點的位移協調方程為

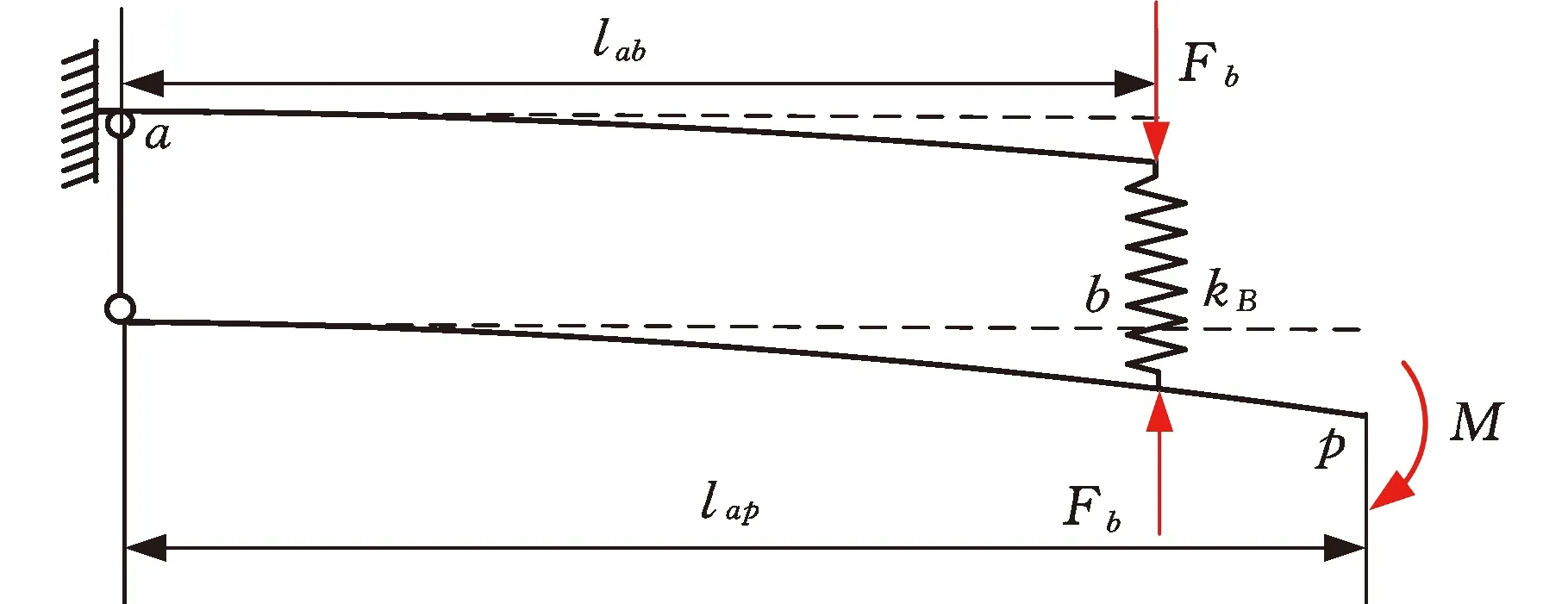
圖4 套齒連接結構等效梁模型(接觸后)Fig.4 Equivalent beam model of spline coupling (after contact)

w1=w2+Δw+wk

(2)

式中，w2為風扇軸b點的徑向位移；wk為接觸變形量。

進一步計算得

(3)

式中，E2、I2分別為風扇軸的彈性模量和截面慣性矩。

進一步化簡式(3)可得b點的作用力Fb：

(4)

則p點的轉角ωp2可表示為

(5)

在不同的變形狀態下，套齒連接結構的彎曲剛度可分段表示為

(6)

隨著彎矩載荷M的增大，套齒連接結構接觸狀態發生變化，彎曲剛度具有分段非線性特征。低壓渦輪軸和風扇軸在定位面B未接觸時，結構的彎曲剛度主要由低壓渦輪軸決定，為一定值；當兩者發生接觸后，結構的彎曲剛度主要由接觸剛度kB決定，隨著載荷的增大，定位面B處的接觸面積和接觸壓力不斷增大，導致接觸剛度kB不斷增大，最終使得彎曲剛度呈現非線性增長的特征。

2 套齒連接結構有限元仿真分析

在不同載荷下，套齒連接結構接觸狀態會發生改變，彎曲剛度也會呈現非線性特征，同時，由于結構不連續，初始配合間隙等結構參數和擰緊力矩、扭矩等裝配參數對結構的剛度特性產生重要影響。因此本節建立套齒連接結構的接觸有限元模型，詳細分析結構彎曲剛度非線性特征的變化規律，討論特征參數對結構彎曲剛度的影響規律。

2.1 套齒連接結構有限元模型

根據套齒聯軸器主要結構特征，忽略螺紋接觸，將軸向鎖緊螺母與低壓渦輪軸固結為整體，省略風扇軸左側錐筒，建立套齒連接結構有限元模型，如圖5所示。模型整體采用高階四面體單元SOLID187劃分網格，在齒的位置進行了局部網格加密。齒根據GB/T 3478.1—2008(圓柱直齒漸開線花鍵標準)，選用30°壓力角圓齒根漸開線花鍵，周向齒數為32個，模數為1.5 mm。

(a)風扇軸

(b)低壓渦輪軸圖5 低壓轉子套齒連接結構有限元模型Fig.5 Finite element model of low-pressure rotor spline coupling

模型的載荷、約束與接觸設置情況如圖6所示，在風扇軸左側施加全約束，低壓渦輪軸右側施加徑向力F，在壓緊面1、壓緊面2、定位面A，定位面B和齒面5個位置，采用CONTA174和TARGE170單元建立接觸對，在鎖緊螺母處使用PRETS179預緊力單元模擬螺栓預緊力。由于定位面A和壓緊面1、2結合狀態穩定，因此不研究其配合參數對整體結構剛度特性的影響，保持接觸對的初始間隙為0，模型材料參數和其他部位的結構參數如表1所示。

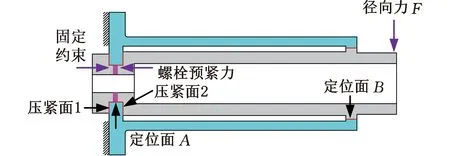
圖6 載荷施加方案示意圖Fig.6 Schematic diagram of load application scheme

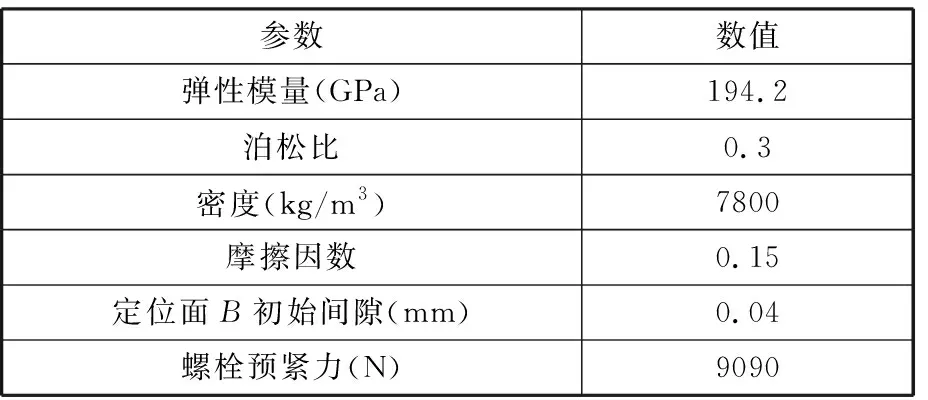
表1 套齒連接結構模型材料與結構參數Tab.1 Model material and structural parameters of spline coupling

2.2 彎曲剛度仿真分析

在套齒連接結構右端施加徑向力F，通過結構右端的徑向變形即彎曲剛度，表征結構的彎曲剛度。徑向力F不同時，彎曲剛度隨徑向力F的變化規律如圖7所示，隨著徑向力F的增大，彎曲剛度呈現明顯的非線性特征，且其變化規律主要分為兩個階段。在第一階段，徑向力F<1 kN時，彎曲剛度基本保持不變，呈略微減小的趨勢，原因在于加載初期徑向力主要作用于低壓渦輪軸，徑向力引起的變形不足以完全抵消已存在的初始間隙，同時齒面和其他接觸面存在滑移的情況，最終使得彎曲剛度在小載荷范圍內呈現減小趨勢。在第二階段，當徑向力F>1 kN時，彎曲剛度開始增大，且逐漸趨于某一定值，原因在于加載中后期徑向力引起的變形抵消了初始間隙，低壓渦輪軸和風扇軸定位面接觸狀態開始改善，接觸區域增大并逐漸趨于穩定。

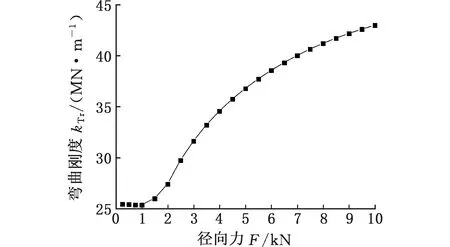
圖7 彎曲剛度隨徑向力的變化規律Fig.7 Variation law of bending stiffness with radial force

不同徑向載荷下，定位面B的接觸狀態如圖8所示，在1 kN徑向力作用下，接觸狀態如圖8a所示，定位面B處于分離狀態。隨著徑向力不斷增大，接觸狀態如圖8b和圖8c所示，定位面B上半部分為分離狀態，下半部分逐漸接觸，出現了滑移和黏滯區，并且黏滯面積逐漸增大，結構整體的變形協調性提高，這是套齒連接結構剛度隨載荷增大而增大的重要原因。當接觸面積與接觸狀態基本不變時，彎曲剛度趨于某一定值。

(a)F=1 kN (b)F=5 kN (c)F=10 kN圖8 不同徑向力下定位面B接觸狀態 (0.04 mm間隙)Fig.8 Contact state of surface B under different radial forces(0.04 mm gap)

2.3 特征參數影響規律分析

2.3.1配合間隙

定位面B初始間隙為0.04 mm和0.02 mm時，彎曲剛度隨徑向力F的變化如圖9所示。從圖中可以看出，不同初始間隙下彎曲剛度變化規律一致，均分為兩個階段：在第一階段，低壓渦輪軸和風扇軸在定位面B處尚未接觸時，不同初始間隙下結構的彎曲剛度大致相同；在第二階段，低壓渦輪軸和風扇軸在定位面B處接觸時，較小的初始間隙可以有效增加套齒連接結構的彎曲剛度。以徑向力F=6 kN為例，配合間隙從0.04 mm減小到0.02 mm時，彎曲剛度由38.5 MN/m增大到45.1 MN/m，彎曲剛度增大約17.1%。

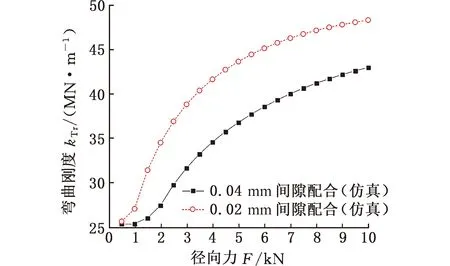
圖9 不同配合間隙下套齒連接結構剛度變化規律Fig.9 Stiffness variation law of spline coupling under different fit clearances

配合間隙為0.02 mm時，不同徑向載荷下定位面的接觸狀態如圖10所示，與圖8配合間隙0.04 mm的接觸狀態相比，小間隙配合結構發生接觸所需的徑向力更小，并且相同徑向載荷下小間隙配合結構的接觸區域相互作用面積更大，導致接觸區域的接觸剛度更大，因此小間隙配合的套齒結構整體彎曲剛度更大。

(a)F=1 kN (b)F=5 kN (c)F=10 kN圖10 不同徑向力下定位面B接觸狀態 (0.02 mm間隙)Fig.10 Contact state of surface B under different radial forces(0.02 mm gap)

2.3.2擰緊力矩

胡適聽說過學校有一個天資過人的女生叫吳健雄，但是他對不上號。他們的相識于是有了一段佳話，還是因為她天資聰穎。有次歷史考試，吳健雄就坐在前排，她只花了兩個鐘頭就把三個小時容量的試卷做完了，還第一個交卷。作為監考老師的胡適很快看完她的卷子，興奮地送到教務室去，正巧學校的兩位名師楊鴻烈、馬君武也在。善作伯樂識人的胡博士激動地告訴他們，他剛看了一份完美的試卷，給了她一百分，因為迄今為止他還沒有看到哪個學生把清朝三百年思想史分析得那么透徹。那兩人立馬也說，班上有一個女生總是考一百分的。于是三人做了個小游戲，各自把這個學生的名字寫下來，拿來一看，不約而同寫的都是“吳健雄”，不禁哈哈大笑。

航空發動機套齒連接結構中鎖緊螺母是關鍵部件之一，它提供的軸向預緊力是保證連接結構穩定的重要參數，會對套齒連接結構剛度特性造成一定的影響。

設置低壓渦輪軸和風扇軸在定位面B處初始間隙為0.04 mm，鎖緊螺母預緊力分別設為6060 N、9090 N以及12121 N，對應于約40 N·m、60 N·m和80 N·m的螺母擰緊力矩，計算不同螺栓預緊力下套齒連接結構的彎曲剛度，其變化規律如圖11所示。結果顯示，不同預緊力下結構彎曲剛度的變化規律基本相同，隨著螺栓擰緊力矩的增大，彎曲剛度略微增大，以徑向力F=6 kN為例，螺栓擰緊力矩從40 N·m增大至80 N·m時，彎曲剛度從38 MN/m大加至38.8 MN/m，彎曲剛度增大約2.1%。因此增大螺母預緊力對提高套齒連接結構的剛度效果不顯著，實際結構中預緊力只要控制在合理范圍內即可。

圖11 不同擰緊力矩下套齒連接結構剛度變化規律Fig.11 Stiffness variation law of spline coupling under different tightening torques

螺栓擰緊力矩主要通過影響壓緊面1和壓緊面2的接觸狀態進而影響結構的彎曲剛度。當徑向載荷較大時，壓緊面1和壓緊面2處于分離狀態，螺栓擰緊力矩對彎曲剛度的影響效果更為明顯，可以明顯觀察到螺栓擰緊力矩對壓緊面接觸狀態的影響。因此選取較大的徑向載荷F=5 kN，此時不同擰緊力矩下壓緊面1和壓緊面2的接觸狀態分別如圖12和圖13所示，壓緊面1呈現出上半部分接觸較好，下半部分分離的接觸狀態，而壓緊面2與之相反，上半部分出現間隙，下半部分處于壓緊的狀態，這種接觸狀態的產生與徑向載荷下壓緊面的受力狀態有關。隨著擰緊力矩的增大，壓緊面1、2的黏滯區域面積開始增大，因此增大預緊力有助于減少壓緊面的分離，進而提高結構的彎曲剛度。但總體而言，螺栓擰緊力矩對彎曲剛度的影響較小，因為在徑向力作用下，低壓渦輪軸和風扇軸類似于懸臂梁結構發生彎曲變形，壓緊面的接觸狀態決定低壓渦輪軸和風扇軸左端變形的耦合效果，但這對整體彎曲變形狀態影響較小，所以對結構彎曲剛度的影響也較小。

(a)40 N·m擰緊力矩 (b)60 N·m擰緊力矩 (c)80 N·m擰緊力矩圖12 不同擰緊力矩下壓緊面1接觸狀態Fig.12 Contact state of pressing surface 1 under different tightening torques

(a)40 N·m擰緊力矩 (b)60 N·m擰緊力矩 (c)80 N·m擰緊力矩圖13 不同擰緊力矩下壓緊面2接觸狀態Fig.13 Contact state of pressing surface 2 under different tightening torques

2.3.3扭矩

設置0、75 N·m和150 N·m的扭矩載荷，計算扭矩載荷對彎曲剛度的影響規律，計算結果如圖14所示。不同扭矩載荷下彎曲剛度的變化規律大致相同，主要分為兩個階段：在第一階段，低壓渦輪軸和風扇軸在定位面B處尚未接觸時，扭矩對彎曲剛度影響較大，彎曲剛度隨扭矩增大明顯增大，并且第一階段對應的徑向力范圍不斷增大，扭矩為0、75 N·m和150 N·m時，一、二階段的分界載荷分別為1 kN、1.5 kN和3.5 kN；在扭矩為150 N·m時，第一階段彎曲剛度的變化規律略有不同，隨徑向力增大彎曲剛度有所增大，因為扭矩較大時，齒面達到較好的接觸效果，內外套齒一定程度上連接了低壓渦輪軸和風扇軸，類似于定位面B起到了一定的支承作用，所以彎曲剛度在第一階段有所增大。在第二階段，低壓渦輪軸和風扇軸在定位面B處接觸之后，扭矩對彎曲剛度的影響有限，以徑向力F=6 kN為例，扭矩從0變化為150 N·m時，彎曲剛度從38.5 MN/m增大至39.5 MN/m，增大約2.6%。套齒連接結構的扭矩主要影響嚙合齒面的接觸狀態，進而影響結構的彎曲剛度。不同扭矩載荷下齒面的接觸狀態如圖15所示，由圖15可知，隨著扭矩的施加，齒面接觸滑移和黏滯面積增大，其抵抗變形的齒面接觸摩擦力增大，有助于加強結構連接的穩定程度，提高結構的彎曲剛度。

圖14 不同扭矩載荷下套齒連接結構剛度變化規律Fig.14 Stiffness variation law of spline coupling structure under different torque loads

(a)無扭矩 (b)75 N·m扭矩(c)150 N·m扭矩

圖15 不同扭矩載荷下套齒齒面接觸狀態變化Fig.15 The contact state of gear surface changes under different torque loads

3 套齒連接結構靜剛度試驗

3.1 試驗裝置及測試系統介紹

套齒連接結構剛度測試裝置總體結構如圖16所示，主要由套齒試驗件及其安裝架、徑向載荷加載裝置、扭矩載荷加載裝置和位移測量裝置構成。套齒試驗件的風扇軸右端法蘭通過螺栓與安裝架相連，安裝架固定于基礎平臺。套齒試驗件低壓渦輪軸的左側法蘭通過螺栓與扭矩加載裝置相連，可通過在掛鉤上添加砝碼實現套齒的扭矩加載。徑向力加載裝置沿套齒連接結構的徑向設置，與低壓渦輪軸相連接，可通過千斤頂實現套齒連接結構的徑向力加載。

圖16 套齒連接結構剛度測試裝置總體結構示意圖Fig.16 Schematic diagram of the overall structure of the stiffness testing device for the spline coupling

套齒連接結構剛度測試現場及測試系統分別如圖17和圖18所示。在套齒連接結構低壓渦輪軸左側法蘭處設置千分表位移測點1，測量精度為0.001 mm。在套齒連接結構風扇軸右側法蘭與安裝架連接處的上邊緣位置設置位移測點2，測量千斤頂向上施加壓力時安裝架的變形量，以便在數據處理時消除它對試驗件端部位移的影響。壓力傳感器依次與應變放大器和信號采集器相連，最終通過計算機進行徑向力的數據采集。

圖17 套齒連接結構剛度測試現場Fig.17 Stiffness experiment scene of spline coupling structure

圖18 套齒連接結構剛度試驗測試系統Fig.18 Stiffness experiment system of spline coupling

3.2 試驗方案

更換不同配合間隙的套齒試驗件、更改鎖緊螺母擰緊力矩、調整扭矩載荷，重復上述步驟，得到定位面配合間隙、擰緊力矩和扭矩三種特征參數對套齒連接結構剛度特性的影響規律。

3.3 試驗結果及分析

3.3.1配合間隙

當扭矩載荷為0、螺母擰緊力矩為60 N·m時，不同配合間隙的套齒連接試驗件徑向力-彎曲剛度關系如圖19所示，可以看出，套齒連接模擬試驗件的剛度隨徑向力增大而增大，原因是隨著載荷增大，定位面B配合間隙逐漸減小直至完全接觸，雙層軸套結構承受載荷，提高了抗變形能力。配合間隙為0.04 mm的套齒結構在徑向力F=1 kN時，未出現試驗結果與仿真結果中剛度保持不變的第一階段，原因是試驗件實際配合間隙小于設計值，徑向力F=1 kN時，定位面B已相互接觸，剛度處于迅速增長階段。0.02 mm配合間隙的套齒結構彎曲剛度試驗值在小載荷區增大較快，大載荷區略微下降繼而趨于平穩，原因是實際配合間隙比設計值小，結構連接緊固程度更高，因此剛度較大，而在大載荷區接觸面出現滑移，因此剛度略微減少。

3.3.2擰緊力矩

當扭矩載荷為0、定位面B處有0.04 mm間隙配合時，取鎖緊螺母擰緊力矩為40 N·m、60 N·m和80 N·m，套齒連接結構彎曲剛度隨徑向力的變化規律如圖20所示。隨著擰緊力矩的增大，套齒連接結構的彎曲剛度有所增大，但增大程度較小，變化規律與套齒連接結構仿真結果一致。在80 N·m擰緊力矩下，大載荷作用范圍內，套齒連接結構的彎曲剛度增大顯著。鎖緊螺母擰緊力矩通過壓緊試驗件中的軸向接觸面提高結構的彎曲剛度。在保證結構安全的前提下，擰緊力矩越大，低壓渦輪軸和風扇軸連接越緊密，套齒連接結構的穩定性越好。

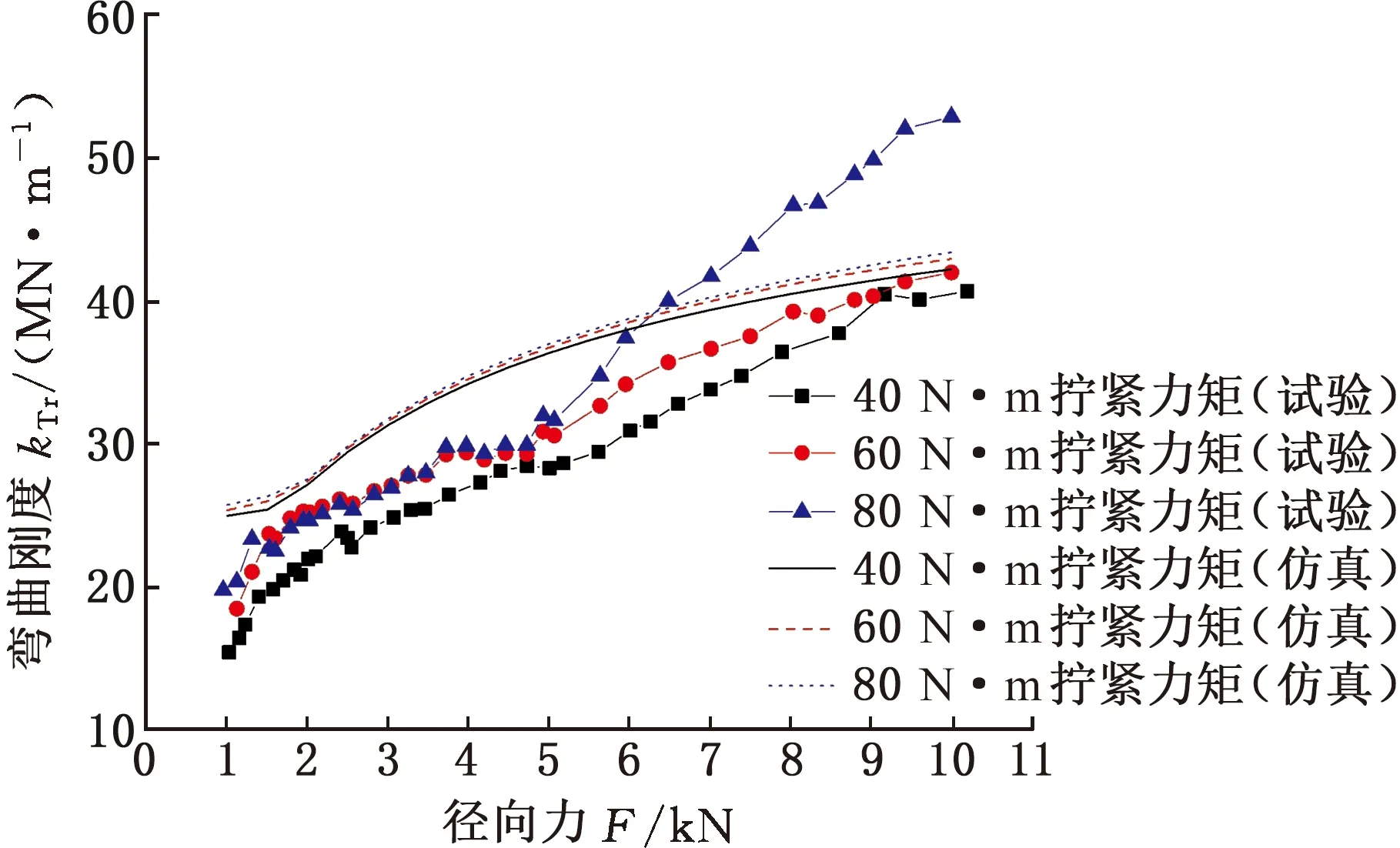
圖20 不同擰緊力矩的套齒剛度試驗與仿真結果對比Fig.20 Comparison of the stiffness experiments and simulation results of spline coupling with different tightening torques

3.3.3扭矩

當定位面B配合間隙為0.04 mm、螺母擰緊力矩為60 N·m時，不同扭矩載荷下套齒連接結構剛度變化規律如圖21所示。試驗結果表明，增大扭矩載荷能提高套齒連接結構的彎曲剛度，尤其是在小載荷階段，增大效果十分明顯，這與套齒連接結構扭矩影響因素的仿真結果一致。在較大扭矩下，套齒連接結構剛度分段非線性特征較為顯著。以75 N·m扭矩為例，當徑向力F<1.5 kN時，結構彎曲剛度基本保持不變，呈略微減小的趨勢，這與彎曲剛度變化的第一階段相符，驗證了彎曲剛度分段非線性變化的正確性。增大扭矩載荷，相當于增大了試驗件中齒面嚙合產生的接觸摩擦力，當結構整體承受徑向載荷時，位于結構中部的齒面嚙合產生的接觸摩擦力抵消了一部分徑向載荷，從而提高了結構的彎曲剛度。

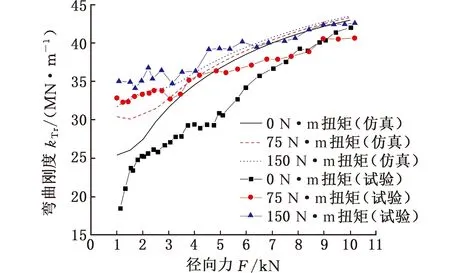
圖21 不同扭矩的套齒剛度試驗與仿真結果對比Fig.21 Comparison of the stiffness experiments and simulation results of spline coupling with different torques

4 結論

(1)不同徑向載荷下，低壓渦輪軸和風扇軸在定位面B處的接觸狀態和受力情況不同，導致套齒連接結構具有分段非線性特征。小載荷作用下，徑向力引起的變形不足以抵消初始配合間隙，套齒連接結構的彎曲剛度主要取決于低壓渦輪軸。隨著載荷增大，低壓渦輪軸和風扇軸在定位面B處產生接觸，套齒連接結構彎曲剛度隨載荷增大不斷增大，并逐漸趨近于某一定值，定位面B接觸面積的增大和接觸狀態的變化是結構剛度不斷變化的重要原因。

(2)建立了考慮齒面接觸的套齒連接結構實體有限元模型，仿真分析了配合間隙、擰緊力矩、扭矩對彎曲剛度的影響規律。減小配合間隙能夠改善定位面B處的接觸狀態，從而有效提高結構的彎曲剛度。擰緊力矩可以影響軸向壓緊面的接觸狀態，但其對彎曲剛度的影響較小。扭矩通過影響嚙合齒面的接觸狀態影響結構的彎曲剛度，在小載荷狀態，扭矩對彎曲剛度的影響十分明顯。

(3)進行了套齒連接結構的靜剛度試驗，驗證了彎曲剛度分段非線性變化特征，以及配合間隙、擰緊力矩和扭矩對彎曲剛度的影響規律。