不同捻制類型多層結構鋼絲繩股力學性能對比研究

陳原培，秦 瑋，何義團

(1. 重慶交通大學 交通運輸學院，重慶 400074； 2. 重慶交通大學 航運與船舶工程學院，重慶 400074)

0 引 言

鋼絲繩具有彎曲柔韌性強、軸向承載能力大、工作性能穩定等優點，通常被用作塔吊、斜拉橋、起重機等工程結構的關鍵部件。在復雜的服役環境中，鋼絲繩受載形式多種多樣，這導致其在工作中容易發生服役性能退化甚至失效報廢，進而可能引起重大工程事故。因此為保障安全生產，探究鋼絲繩服役性能尤為重要。

對于鋼絲繩服役性能，國內外學者進行了廣泛的研究。G.A.COSTELLO[1]提出了鋼絲繩理論，該理論包含了鋼絲繩的結構、摩擦特性、靜力學特性等內容，為鋼絲繩研究提供了重要理論參考；蘭成民等[2-3]建立了鋼絲繩疲勞壽命模型，推導了鋼絲疲勞破壞循環次數，并在此基礎上提出了疲勞壽命極限估計方法；張德坤等[4]對6×19提升鋼絲繩的摩擦磨損性能進行了研究；E.Z.XING等[5]研究了鋼絲繩在微重力和零張力影響下的彎曲特性；W.G.JIANG[6]建立了具有精確彎曲對稱邊界條件的簡單鋼絲繩有限元模型，并驗證了其正確性；馬軍等[7]通過對不同捻距的鋼絲繩進行有限元仿真，得出了捻距倍數對鋼絲繩應力的影響規律；李紅等[8]基于鋼絲波導頻散曲線，結合有限元方法分析了鋼絲模態轉角受拉力影響的變化規律；D.G.WANG等[9]針對1×19及6×19+IWS的多層結構鋼絲繩進行了有限元仿真，分析了兩類鋼絲繩的疲勞壽命；張奔牛等[10]通過鋼絲的應力和振蕩頻率間的關系檢測鋼絲中的預應力程度；L.LIU等[11]采用分層計算和直接計算兩種計算模式對7×7鋼絲繩股的力學性能進行了評估，其結果表明初始螺旋角對鋼絲繩拉伸及扭轉性能有顯著影響；陳原培等[12]通過有限元分析，對不同類型鋼絲繩的拉伸及扭轉性能差異進行了探討，并基于半解析法對變載荷鋼絲繩進行了全接觸分析，繼而分析了繩間接觸對鋼絲繩力學性能的影響。

綜上可知，學者們對鋼絲繩服役性能進行了諸多研究。然而對于已被廣泛應用的多層結構鋼絲繩，由于其空間捻制的多樣性與復雜性，不同捻制類型的鋼絲繩間存在何種性能差異，以及該差異對其應用具有何種影響等問題，以往研究很少涉及。對此，筆者以具有多層結構的單股鋼絲繩(簡稱：多層結構鋼絲繩股)為研究對象，考慮鋼絲彈塑性、絲間摩擦和接觸等影響因素，建立交互捻多層結構鋼絲繩股和同向捻多層結構鋼絲繩股的參數化幾何模型和有限元模型，探究兩類繩股在拉伸載荷作用下的性能差異，以期為鋼絲繩的設計與選用提供一定參考。

1 理論建模

1.1 多層結構鋼絲繩股參數化幾何模型

多層結構鋼絲繩股復雜的空間結構影響其服役性能，為對繩股力學性能進行分析，精確建模十分重要。

建立了由芯絲(簡稱：CW)、內層側絲(簡稱：IW)和外層側絲(簡稱：OW)組成的兩類多層結構鋼絲繩股，其幾何結構如圖1。交互捻多層結構鋼絲繩股芯絲為mC根直徑為DC的直鋼絲，內層側絲為mI根直徑為DI的鋼絲以βI(約定右捻時捻角為正值，左捻時捻角為負值)的捻角捻制而成，外層側絲則由mO根直徑為DO的鋼絲以βO的捻角捻制而成，且內層與外層側絲捻向相反；同向捻多層結構鋼絲繩股除外層側絲捻向與交互捻繩股相反外其他所有幾何參數均與交互捻繩股相同。

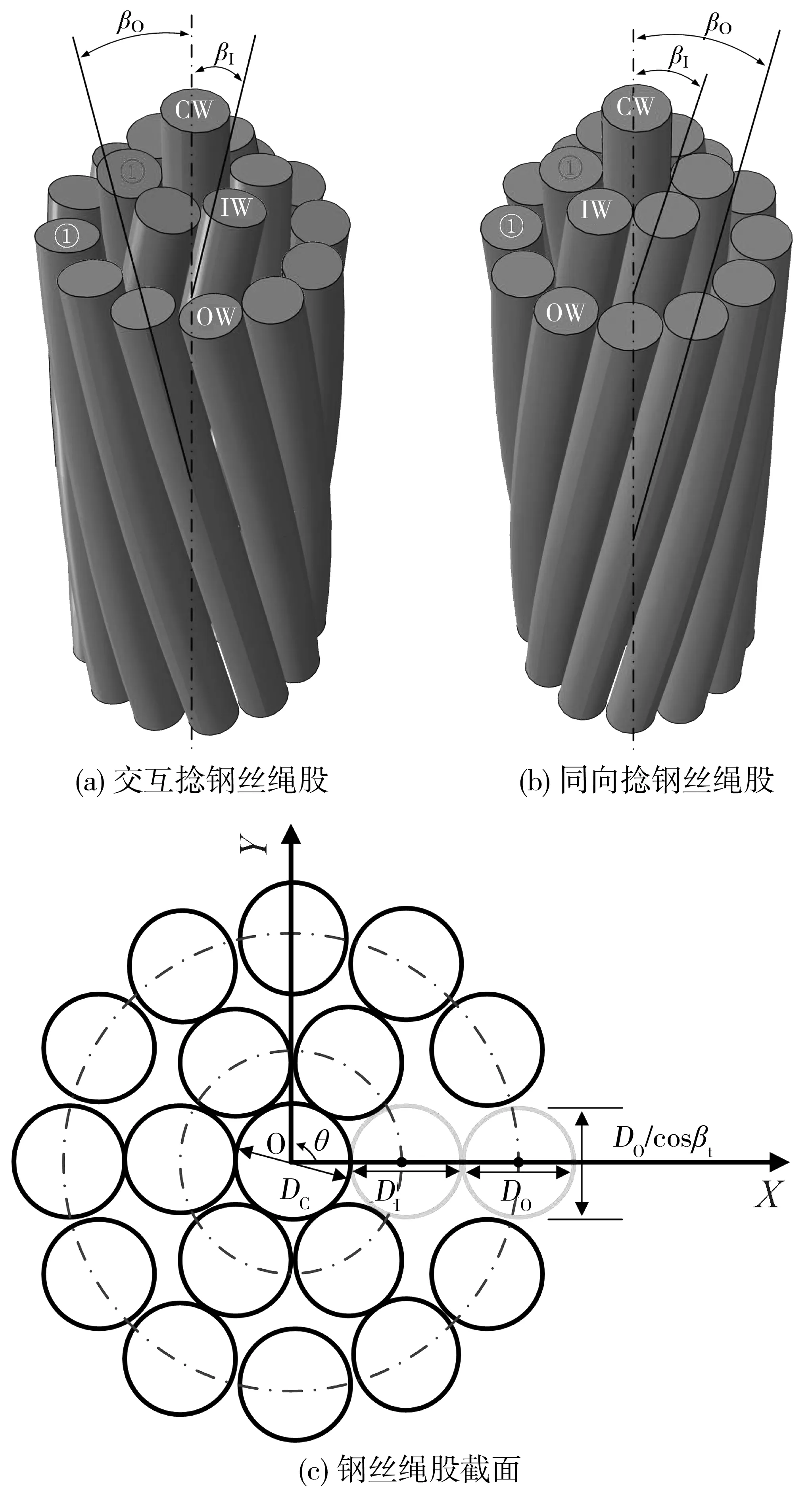
圖1 多層結構鋼絲繩股幾何特征

建立原點為芯絲圓心的笛卡爾直角坐標系，使鋼絲繩股的軸線方向為Z軸，X和Y軸如圖1(c)。投影XY平面，則投影坐標(0，0)為芯絲中心，內層和外層側絲在XY平面上的投影則為橢圓，其長軸和短軸分別為at=Dt/cosβt和bt=Dt(t=I或O)。因此，兩類繩股側絲空間曲線方程為：

Xtj=rtcosθ

(1)

Ytj=rtsinθ

(2)

Ztj=rtθtanβt+(j-1)st

(3)

式中：θ為繞繩軸的周向坐標；j為各層螺旋側絲的標號，即j=1,2,3…,mt，其中mt為側絲數(t=I或O，內層側絲數mI=6，外層側絲數mO=12)；rt為側絲軸線螺旋半徑，其中rI=(DC+DI)/2，rO=DI+(DC+DO)/2；βt為各側絲的捻角；st=2πrcotβt/mtv為鄰近側絲的軸向距離(t=C或I)。

通過上述推導的參數方程，使用Pro/E軟件建立交互捻多層結構鋼絲繩股和同向捻多層結構鋼絲繩股的參數化幾何模型。筆者假定兩類繩股的初始接觸僅為徑向接觸(即CW-IW接觸和IW-OW接觸)而無周向接觸(即IW-IW接觸和OW-OW接觸)，此處初始接觸表示只發生接觸但并未任何接觸應力。為此，各幾何參數需滿足以下條件[13]：

(4)

(5)

合理的鋼絲繩股模型長度是對其進行分析的重要環節，過大的模型長度將增加計算負擔而顯著降低求解效率，模型長度過短將引起終端效應而影響分析結果的準確性。因此，為保證仿真分析的計算效率和精確度，筆者使用W.G.JIANG[6]的方法，以多層結構鋼絲繩股1/6的最大捻距作為繩股股長L，本研究中取股長L為45 mm。表1為兩類繩股幾何參數。

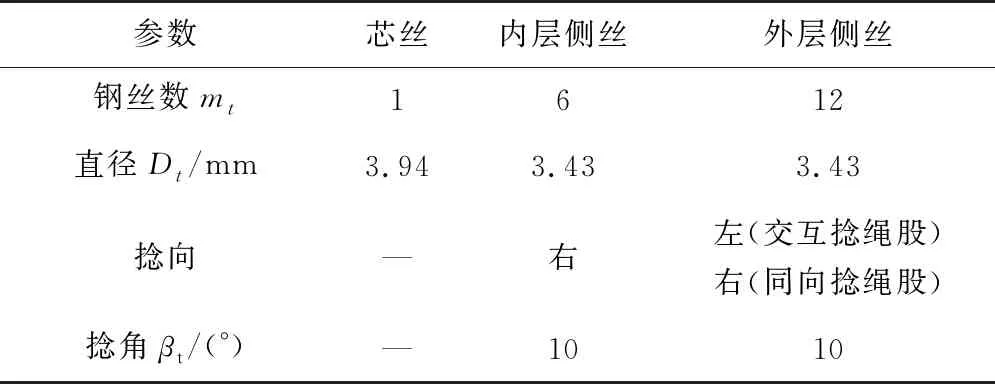
表1 多層結構鋼絲繩股幾何參數

1.2 多層結構鋼絲繩股有限元模型

在1.1節建立的兩類多層結構鋼絲繩股幾何模型的基礎上，通過ABAQUS建立繩股的有限元模型。繩股材料特性參數為[6,14]：楊氏模量E=188 GPa，塑性模量EP=24.6 GPa，泊松比γ=0.3，屈服應力σY=1.54 GPa。此外，假定鋼絲材料為各向同性，則根據材料強化準則可得屈服函數f：

f=σVM-h(εP)

(6)

式中：h(εp)為屈服強度函數；εp為累積等效塑性應變；σVM為von Mises應力，假定鋼絲材料均符合雙線性硬化準則，則h(εp)為[12]：

(7)

本研究采用ABAQUS進階算法并以C3D8R八節點六面體單元進行繩股的網格劃分，線性縮減積分適用于塑性、蠕變、大撓度等工況，能更好地模擬大變形[15]。圖2為兩類繩股網格劃分結果。

圖2 多層結構鋼絲繩股網格模型

如前所述，在多層結構鋼絲繩股模型建立時考慮了徑向初始接觸。而同層鋼絲間的周向接觸在加載過程中也可能發生。因此在罰函數Augmented-Lagrangian算法的基礎上對絲間接觸壓力進行迭代求解，接觸壓力P為：

(8)

式中：sz為判斷絲間是否發生干涉的接觸間隙，其為負值則發生干涉，反之則未干涉；γz為用于增強計算效果的額外因子；Kz為接觸剛度。絲間摩擦剪切力Ff可由Coulomb摩擦定理得到：

Ff=μP

(9)

式中：μ為摩擦系數，筆者取0.115[6]。另外，各節點處平衡方程為：

Fn=ku

(10)

式中：Fn、k和u分別為節點力矩陣、總剛度矩陣和節點位移矩陣。

考慮到多層結構鋼絲繩股絲間復雜的多種接觸狀態，筆者將硬接觸作為接觸設定，以主從接觸算法進行接觸面間傳遞載荷。多層結構鋼絲繩股進行拉伸有限元分析時，分別在鋼絲繩股兩端面創建參考點RP-1和RP-2，并分別與其所對應的端面進行運動耦合，再約束其6個自由度，并以逐步加載的方式對繩股模型進行加載。具體加載方式為：完全固定兩類多層結構鋼絲繩股的參考點RP-2，并將RP-1關于Z軸的旋轉自由度UR3進行約束，對RP-1施加以0.001為步長，最大為0.01的沿Z軸的拉伸應變，其余自由度不做約束。圖3為約束及加載方式。

圖3 多層結構鋼絲繩股約束及加載示意

2 模型有效性驗證

分別對兩類繩股進行幾何模型和有限元分析模型的校核。首先，為確保繩股幾何模型滿足前文所述的絲間初始接觸條件，通過Pro/E軟件幾何干涉工具進行檢查。對于有限元模型，通過對繩股進行拉伸仿真分析，并與G.A.COSTELLO[1]彈性理論結果和D.G.WANG等[9]的分析結果進行對比的方式驗證。由于兩類繩股的加載和約束施加方式相同，在此僅選取同向捻多層結構鋼絲繩股來進行驗證。

2.1 網格靈敏度分析

有限元分析結果受到網格密度的直接影響，低密度網格不能保障精確度；高密度網格精度高，但將顯著增加計算時間和資源，因此合適的網格密度十分必要。對此，筆者以交互捻多層結構鋼絲繩股有限元模型為例進行了網格靈敏度分析。繩股加載和約束方式與圖3相同。表2為3種不同網格密度下得到的軸向力FN、扭矩MN和von Mises應力，表2中還給出了各密度網格相對于最大密度網格的相對誤差。

由表2可知，仿真結果受到網格密度影響，各結果數值隨著網格密度的增大，而趨于平穩。網格密度越高所得結果越精準，但計算負擔也隨之增加。對比表2結果可知，b類網格所有結果值相對誤差均不超過2%，在合理誤差范圍內，因此筆者以該密度網格進行兩類繩股的拉伸有限元分析。

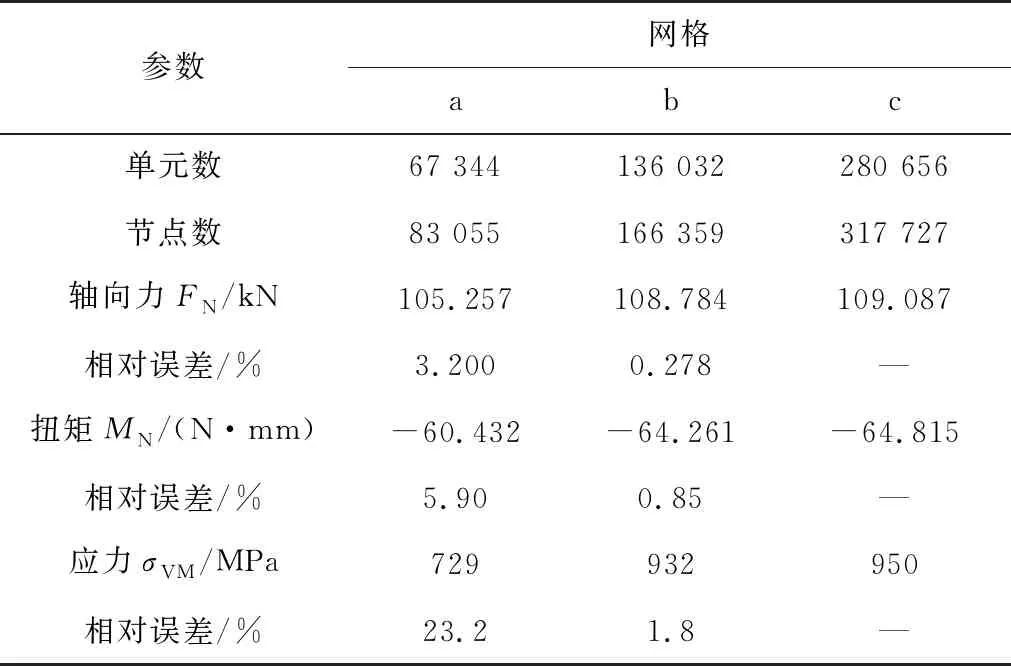
表2 網格靈敏度分析

2.2 結果對比

為驗證中有限元模型，筆者采用的鋼絲幾何參數如表3。此外，股長L=9 mm，鋼絲彈性模量E=203 GPa，泊松比為γ=0.3，塑性模量EP與文獻[9]相同。驗證結果對比如圖4。

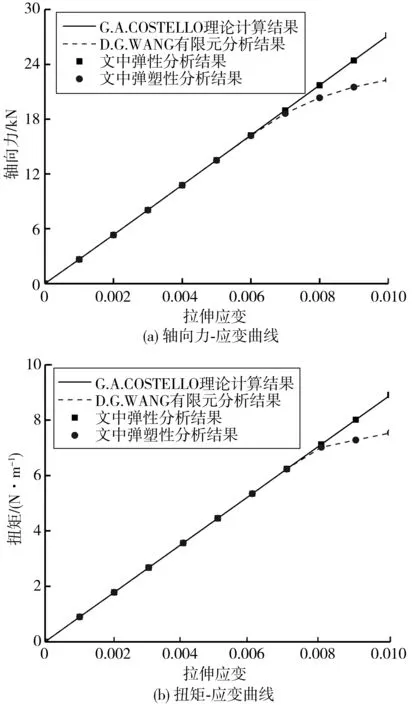
圖4 多層結構鋼絲繩股有限元模型驗證

表3 驗證模型幾何參數

結果表明：本模型純彈性結算結果與G.A.COSTELLO彈性理論一致；在考慮鋼絲彈塑性后，本模型計算結果與D.G.WANG等[9]的結果十分吻合，拉伸應變達到0.007后繩股將發生塑性變形，彈塑性計算結果低于彈性計算結果。由上述可知，筆者所建立的多層結構鋼絲繩股有限元模型準確有效。

3 結果與討論

在筆者所建立的交互捻和同向捻多層結構鋼絲繩股有限元模型基礎上，分別對其進行拉伸有限元仿真，并分析兩者的性能差異及其在實際應用產生的影響。圖5為交互捻和同向捻多層結構鋼絲繩股在軸向拉伸載荷下的結果對比。其中，軸向力值為正表示其為沿Z方向拉伸，反之則為沿Z方向壓縮；扭矩值為正表示關于繩股軸線方向的扭矩與右旋方向一致，反之則相反。由圖5可知，拉伸初始階段，兩類繩股的軸向力和扭矩隨著拉伸應變的增加近似線性增加，且均未發生塑性變形；當拉伸應變達到0.006左右時，絲間接觸發生了應力屈服，產生了塑性變形，軸向力和扭矩增加速率降低。由圖5(a)可知，同向捻繩股的扭矩方向與其右捻向相同，而交互捻與左旋方向一致且絕對值比同向捻繩股小，表明交互捻鋼絲繩股受拉伸載荷時具有更好的抗旋轉性能。

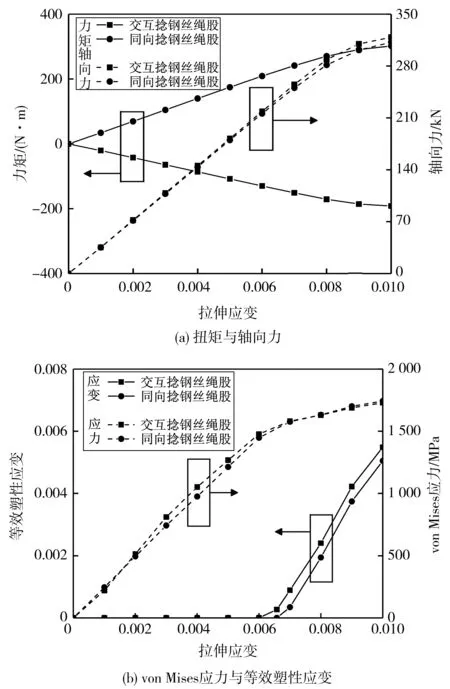
圖5 交互捻鋼絲繩股和同向捻鋼絲繩股拉伸性能對比

由圖5還可知，拉伸加載結束時，交互捻和同向捻繩股最終von Mises應力差值并不大，可見兩類多層結構鋼絲繩股的整體應力受拉伸載荷影響相近。0.01拉伸應變時，交互捻繩股產生塑性應變比同向捻繩股更大，表明交互捻繩股更易發生應力屈服。

圖6為交互捻和同向捻鋼絲繩股應力應變分布。由圖6可知，拉伸載荷下，兩類繩股的絲間接觸狀態相同，即芯絲-內層側絲接觸和內層側絲-外層側絲接觸，兩類接觸產生的應力均以60°角為周期呈圓周對稱式分布。等效塑性應變分布規律與應力分布規律一致，對比應變分布可知，交互捻繩股在內層側絲-外層側絲間的接觸位置產生最大塑性應變，而同向捻繩股在芯絲-內層側絲間接觸部位發生，且前者大于后者。上述區別的原因在于交互捻繩股內層和外層側絲的捻向不同，二者絲間點接觸產生了比芯絲-內層側絲間線接觸更大的接觸應力，因而產生更大的塑性應變。

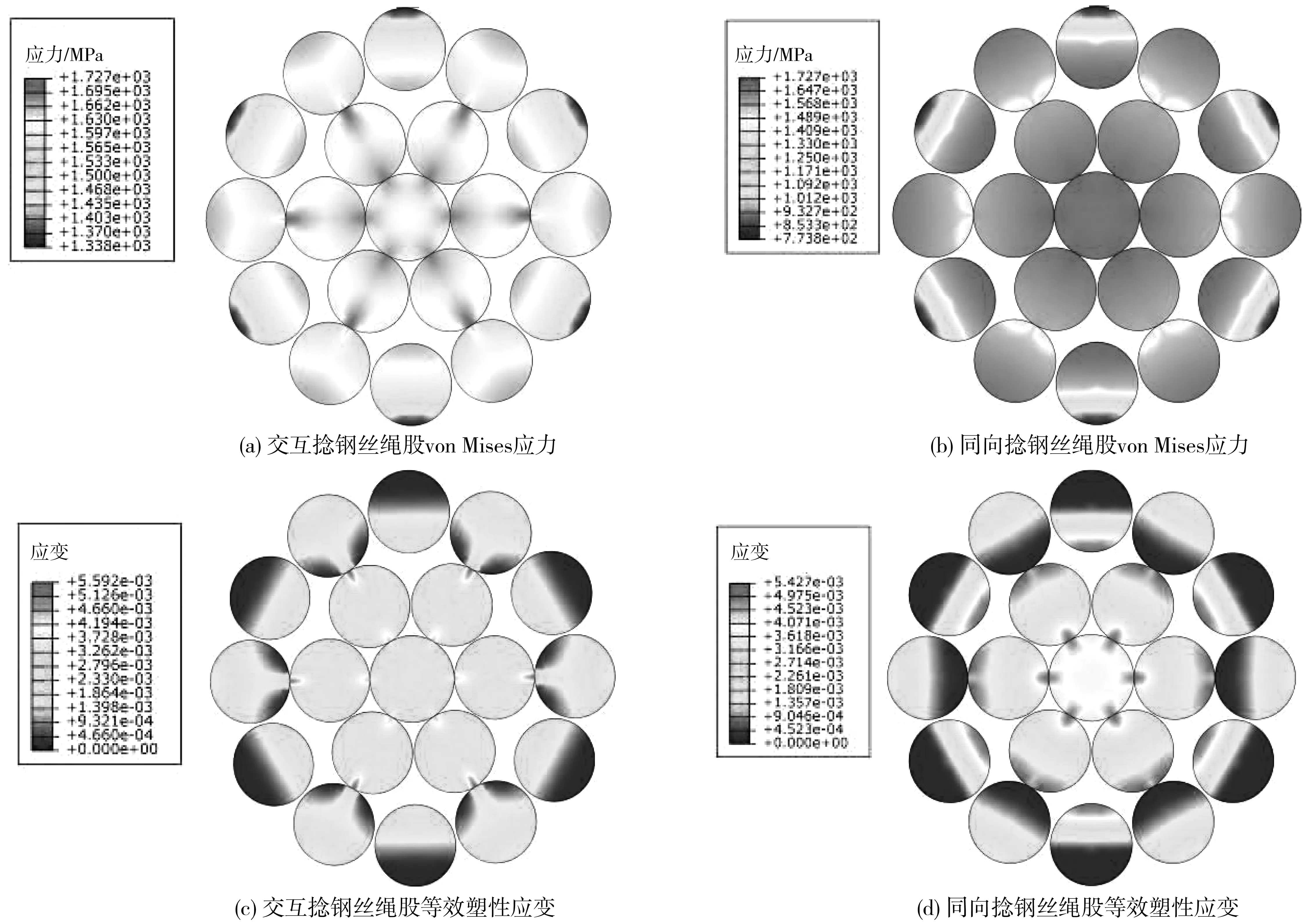
圖6 拉伸載荷下交互捻鋼絲繩股和同向捻鋼絲繩股應力應變分布

為進一步探討交互捻和同向捻繩股服役性能差異，筆者對比分析了兩類繩股局部性能參數。

圖7為兩類繩股von Mises應力和等效塑性應變沿繩股徑向，即圖1(c)中X軸方向結果對比。由圖7可知，兩類繩股的von Mises應力和等效塑性應變沿繩股徑向變化趨勢相似。交互捻繩股在繩股芯層產生的應力和塑性應變小于同向捻繩股。兩類繩股的應力應變值均沿徑向逐漸增加，并在芯絲-內層側絲(CW-IW)接觸位置達到第1個峰值。隨著徑向距離的進一步增大，交互捻繩股在內層側絲的結果先減小后增大，并在內層側絲中部達到局部最小，在內層側絲-外層側絲(IW-OW)接觸處達到最大值；而同向捻繩股在內層側絲的結果逐漸減小，并在IW-OW接觸處達到最小值。上述現象發生的原因在于，交互捻繩股不同的內外層側絲捻向，從而以點接觸形式產生鋼絲內部應力，導致拉伸過程中CW-IW接觸點應力與IW-OW接觸點結果相當，進而在內層側絲芯部形成低應力區；對于同向捻繩股，內外接觸點產生的應力相差較大，使內層側絲產生沿徑向方向的遞減應力區。由圖7還可知，等效塑性應變的變化趨勢與應力變化趨勢相對應，交互捻繩股塑性變形最大發生在IW-OW接觸部位，而同向捻繩股發生在CW-IW接觸部位。

圖7 交互捻鋼絲繩股和同向捻鋼絲繩股徑向結果對比

對于不同絲間接觸類型產生的性能差異，圖8給出了拉伸加載過程中交互捻和同向捻繩股各層鋼絲間接觸界面位置的最大von Mises應力與最大等效塑性應變演變情況。由圖8(a)可知，兩類繩股在芯絲-內層側絲(CW-IW)接觸部位具有相近的結果：應力均隨拉伸應變的增加而線性增加，且均在應變達到0.006后發生應力屈服而產生塑性變形，隨后因材料硬化而較屈服前應力增加速率有所減小，同時繩股發生屈服后等效塑性應變均隨拉伸應變呈近似線性增加趨勢。圖8(b)則表明：兩類繩股在內層側絲-外層側絲(IW-OW)接觸區的應力應變演變規律存在一定異同，兩類繩股應力均以“雙線性”規律增加，但加載初期交互捻繩股應力增加率明顯大于同向捻繩股，后者晚于前者發生應力屈服和塑性變形，以致前者的最終塑性應變約為后者的5倍。由上述可知，同向捻繩股在拉伸載荷工況下具有更好的抗屈服性及徑向受載能力。

圖8 交互捻和同向捻鋼絲繩股不同接觸區應力應變對比

圖9為交互捻和同向捻繩股各層鋼絲在軸向拉伸載荷下的承載分布。由圖9可知，兩類繩股各層鋼絲具有相近的軸向力變化趨勢，其中外層12根側絲(OW)的軸向力最大，內層6根側絲(IW)次之，芯絲(CW)軸向力最小。對于拉伸載荷引起的鋼絲扭矩，兩類繩股結果存在明顯差異：交互捻繩股各層絲扭矩方向并不都相同，CW無扭矩作用，IW與右旋一致，而OW所受扭矩與左旋一致，整股所受扭矩方向與OW相同；同向捻繩股內外層側絲具有相同的扭矩方向，且芯絲同樣不受扭矩作用，IW扭矩大于OW，且交互捻繩股的總扭矩小于同向捻繩股，由此可知，前者抗旋轉性能優于后者。由上述可知，捻向對拉伸載荷作用下鋼絲繩股的軸向力影響較小，而對其扭矩影響顯著，該發現與L.LIU等[11]的研究結論一致。

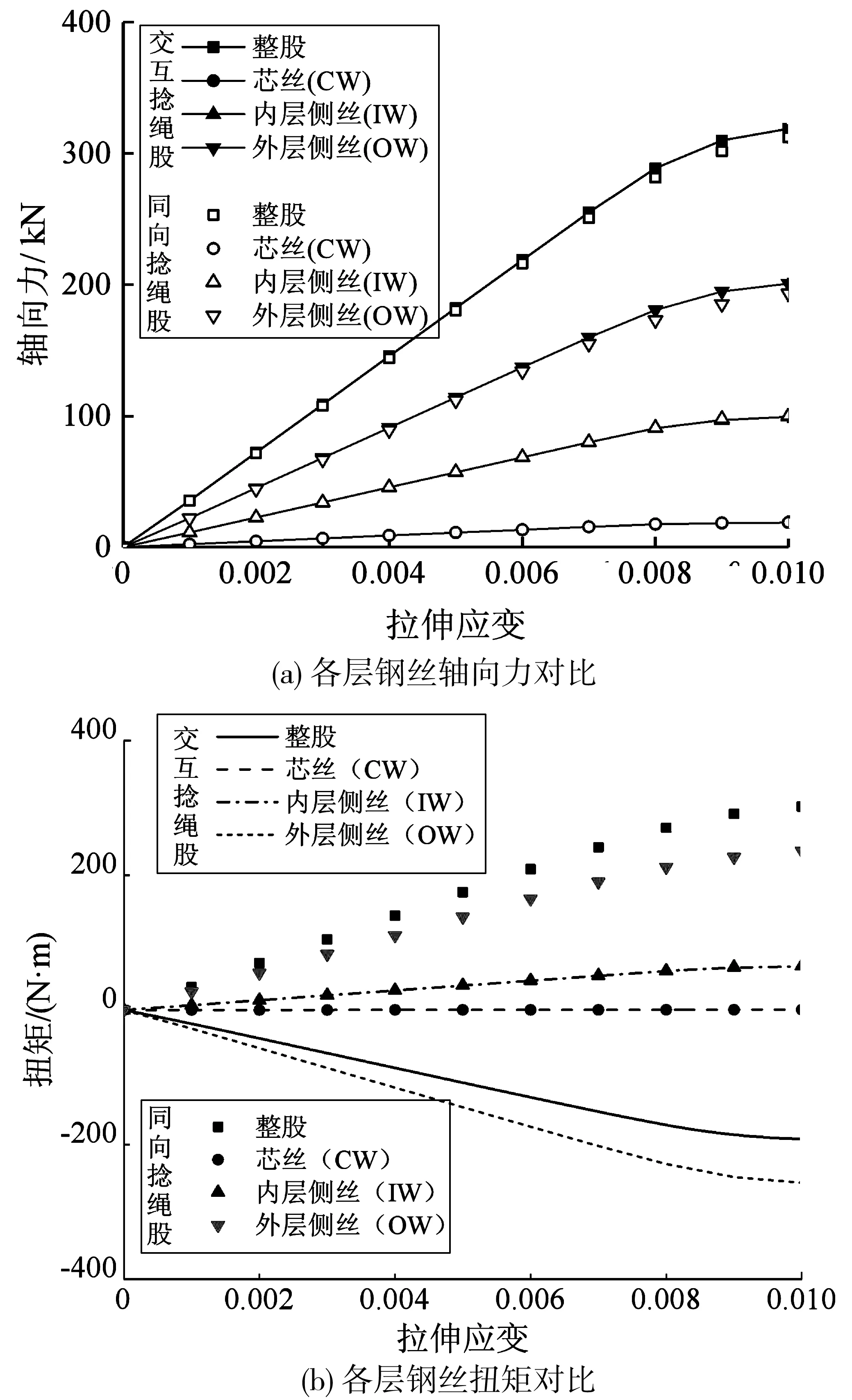
圖9 交互捻和同向捻鋼絲繩股各層鋼絲承載分布對比

交互捻和同向捻多層結構鋼絲繩股各層單根鋼絲軸向力對比結果如圖10。由圖10可知，兩類繩股各層單根鋼絲的軸向力隨拉伸應變的變化趨勢相同，均表現為先近似線性增大，在達到應力屈服后增加速率逐漸減小。相同拉伸應變下，兩類繩股各層單根鋼絲的軸向力均表現為：芯絲(CW)最大，內層側絲(IW)次之，外層側絲(OW)最小，該結論與D.G.WANG等[9]所提及的結論相符，且二者在相同位置的單根鋼絲所受的軸向力近似相同，由此可知，捻制方式對繩股單根鋼絲軸向力影響較小。

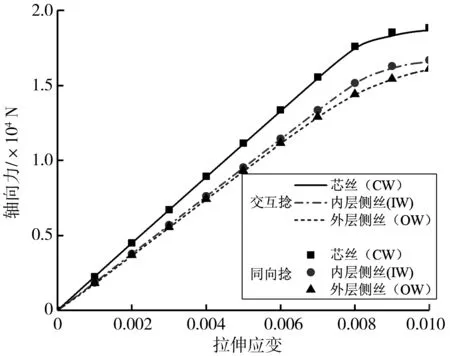
圖10 交互捻和同向捻鋼絲繩股各層單根鋼絲軸向力對比

4 結 論

建立了交互捻和同向捻多層結構鋼絲繩股的參數化幾何模型，并考慮鋼絲彈塑性、絲間摩擦和接觸等因素，建立了上述兩類鋼絲繩股的有限元模型，對比分析了二者在軸向拉伸載荷作用下的服役性能差異，所得主要結論如下：

1)兩類繩股在相同拉伸應變下具有相近的軸向力和von Mises應力，二者抗拉性能相當；相比于同向捻繩股，交互捻繩股產生了較小的扭矩，因而表現出較好的抗旋轉性。

2)交互捻和同向捻繩股內層側絲的應力應變沿繩股截面半徑方向的變化明顯不同，前者在芯絲-內層側絲接觸區達到峰值后減小，隨之又增加，并在內層側絲-外層側絲達到最大值，而后者則沿徑向一直減小。

3)拉伸過程中，交互捻繩股內層側絲-外層側絲接觸處應力集中更明顯，而同向捻繩股芯絲-內層側絲接觸處應力集中更突出；前者比后者更早發生塑性應變且最大塑性應變相差較大。

4)兩類繩股的各層鋼絲在拉伸過程中有近似相等的軸向力變化趨勢；兩類繩股芯絲均未產生扭矩，交互捻繩股內外層側絲扭矩方向相反，整體扭矩與外層側絲相同，都與左旋方向一致，同向捻繩股各側絲及整股扭矩方向均與右旋方向一致，上述差異導致二者抗扭性能的不同。

5) 拉伸載荷下，捻制方式對多層結構鋼絲繩股各層單根鋼絲軸向拉力的影響較小，且各層單根鋼絲軸向力由大到小為：芯絲最大，內層側絲次之，外層側絲最小。